Талант против удачи: роль случайности в успехе и провале

06.06.2019

Недавно я натолкнулся на интересную работу итальянских учёных о сильно недооценённой роли удачи и случайности в нашей жизни. К сожалению, не нашёл полной версии на русском языке (может, плохо искал?), но очень уж хотелось поделиться прочитанным со своими не владеющими английским товарищами. Поэтому, засучив рукава, принялся за свой кустарный перевод. Авторы, Аллесандро, Алессио и Андреа, любезно разрешили опубликовать его в общем доступе, поэтому, если заинтересовались, добро пожаловать под кат.

Авторы

А. Плучино – кафедра физики и астрономии, Катанийский университет и Катанийский филиал Национального института ядерной физики, Италия; alessandro.pluchino@ct.infn.it
А. Е. Биондо – кафедра экономики и бизнеса, Катанийский университет, Италия; ae.biondo@unict.it
А. Раписарда – кафедра физики и астрономии, Катанийский университет и Катанийский филиал Национального института ядерной физики, Италия; Центр изучения сложных систем, Вена; andrea.rapisarda@ct.infn.it

Аннотация

В значительной степени доминирующая меритократическая (меритократия – принцип управления, согласно которому руководящие посты должны занимать наиболее способные люди, независимо от их социального происхождения и финансового достатка) модель высококонкурентных Западных культур берет начало из веры в то, что успех в основном, если не полностью, зависит от личных качеств, таких как талант, интеллект, навыки, находчивость, трудолюбие, упорство, тяжёлый труд или принятие рисков. Порой мы готовы признать, что определенная доля удачи тоже может играть роль в достижении значительного материального успеха. Но, по правде говоря, довольно часто недооценивается важность внешних сил в отдельных историях успеха. Хорошо известно, что интеллект (или, в общем, талант и личные качества) в популяции имеет гауссово распределение, в то время как распространение ценностей — часто рассматриваемое в качестве мерила успешности — обычно следует степенной зависимости (закону Парето), когда большинство являются бедняками и есть ничтожно малое количество миллиардеров. Такое расхождение между нормально распределенными входными данными, имеющими обычный уровень (усредненные талант или интеллект) и неизменным распределением на выходе, наводит на мысли, что где-то за кулисами имеется невидимый компонент. В данной работе, на основе крайне простого и игрушечного агентного моделирования, мы делаем предположение, что таким компонентом является обычная случайность. В частности, мы показываем, что, хотя для жизненного успеха действительно и правда требуется некоторая доля таланта, но самые одарённые люди практически никогда не достигают высочайших вершин благосостояния, будучи обогнанными посредственными, но намного более удачливыми личностями. Насколько нам известно, этому противоречащему здравому смыслу результату — хотя и неявно предполагаемому между строк много в какой литературе — именно тут впервые дана количественная оценка. Это позволяет по-новому взглянуть на эффективность оценки достоинств на основе уже достигнутого уровня успеха и подчеркивает риски распространения чрезмерных почести или ресурсов людям, которые, в конечном счёте, могли оказаться просто удачливей остальных. При помощи данной модели также рассматриваем и сравниваем несколько поведенческих гипотез, чтобы показать наиболее эффективные стратегии государственного финансирования исследований, с целью для улучшения меритократии, разнообразия и инновационности.

1. Введение

Повсеместность степенной зависимости во многих физических, биологических или социо-экономических сложных системах можно рассматривать как нечто вроде отличительного математического признака тесной взаимосвязи их динамичной характеристики с масштабно-неизменяемой топологической структурой [1, 2, 3, 4]. В социо-экономическом контексте, по работе Парето [5, 6, 7, 8, 9], хорошо известно, что распределение богатств имеет характер степенной зависимости, чья характерная сильно вытянутая форма отражает глубину существующей пропасти между богачами и бедняками нашего общества.

Недавний отчет [10] показывает, что на сегодня данный разрыв намного больше, чем мы опасались: восемь людей владеют теми же богатствами, что и 3,6 миллиарда человек, составляющих беднейшую часть человечества. За последние 20 лет было выработано несколько теоретических моделей, вычисляющих распределение ценностей в контексте теории вероятностей и физической статистики, часто принимающих вид мультиагентного моделирования с простыми внутренними динамиками [11, 12, 13, 14, 15, 16, 17].

Двигаясь дальше в этом направлении, если рассматривать личное богатство как мерило успеха, то можно утверждать, что глубоко ассиметричное и неравное его распределение среди людей является следствием их естественных различий в таланте, навыках, компетенции, интеллекте, способностях или мере их упорства, трудолюбия, либо целеустремлённости. Такое предположение, в неявной форме, является основой так называемой меритократичной парадигмы: оно влияет не только на то, каким образом наше общество предоставляет возможности трудоустройства, чествование и славу, но также на стратегии, принятые правительствами для распределения ресурсов и финансирования тем, кто считаются наиболее заслуженными личностями.

Однако, предыдущий вывод, похоже, сильно расходится с подтверждёнными данными, что упомянутые выше свойства и качества людей нормально распределены по всей популяции, т.е., соответствуют симметричному Гауссовому распределению относительно данного среднего. Например, интеллект, каким он измеряется посредством тестов на IQ, соответствует следующему шаблону: средний IQ равен 100, но ни у кого нет IQ 1000 или 10000. То же относится к труду, считаемому в рабочих часах: кто-то работает больше среднего, другой меньше, но не существует того, кто трудится в миллиард раз больше часов по сравнению с остальными.

Зато в наше время появляется все больше доказательств касательно основополагающей роли шанса, удачи или, обобщая, случайных факторов, в определении успехов или провалов в наших личных и профессиональных делах. В частности, было показано, что все ученые имеют одинаковый шанс опубликовать в течение карьеры прорывную работу [18]; что те, у кого первая буква фамилии находится ближе к началу алфавита, намного вероятней получат должность начальника отдела [19]; что распределения библиометрических показателей, собранные учеными, могут оказаться случайными и бессмысленными из-за растущего явления, связанного с инфляционным механизмом «публикуйся или погибай» [20]; что позиция кого-либо в отсортированном по алфавиту списке может оказаться важной при определении доступа к ограниченным по количеству мест публичным сервисам [21]; что начальная буква отчества поднимает оценку интеллектуальных способностей [22]; что людей с легко произносимыми именами оценивают более положительно, чем тех, чьи имена сложные [23]; что те, чьи имена звучат более аристократично, чаще остальных работают в качестве руководителей, а не подчинённых [24]; что женщины с мужскими прозвищами более успешны в юридической профессии [25]; что примерно половина различий в доходах среди людей всего мира объясняется исключительно их страной проживания и распределением зарплат внутри соответствующей страны [26]; что на вероятность стать директором сильно влияют ваши имя и месяц рождения [27, 28, 29]; что инновационные идеи являются результатом случайных реакций в клетках нашего мозга [30]; и что даже вероятность развития рака, вполне возможно, разрушающего великолепную карьеру, по большей части зависит от неудачливости [31, 32]. Последние работы на тему репродуктивного успеха в течение жизни способствуют подтверждению таких высказываний, показывая, что, если отклонения признаков могут влиять на судьбу популяции в целом, то жизнь конкретных особей зачастую определяет удача.

В последние годы многие авторы, среди которых есть статистик и аналитик рисков Нассим Талеб [35, 36], инвестиционный стратег Майкл Мобуссин [37] и экономист Роберт Франк [38], исследовали в ряде популярных книг связь между удачей и мастерством в финансовых операциях, бизнесе, спорте, искусстве, музыке, литературе, науке и многих других областях. Они пришли к заключению, что случайные события играют гораздо большую роль в жизни, чем многие могли бы себе вообразить. На самом деле, они не предполагают, что успех не зависит от таланта и приложенных усилий, так как в крайне конкурентных областях или рынках типа «победитель забирает все», где мы живем и работаем в данное время, наиболее результативные люди практически всегда при этом необычайно талантливы и трудолюбивы. Они лишь заключили, что таланта и усилий недостаточно: вам также необходимо оказаться в нужном месте в нужное время. Короче говоря, удача также влияет, хотя её роль практически всегда недооценивается успешными людьми. Такое происходит из-за того, что случайность часто срабатывает неочевидным образом, поэтому легко сопоставить события, которые покажут успех как нечто, являвшееся неизбежным. Талеб называет такую наклонность «сказательным заблуждением» [36], а социолог Пол Лазарсфельд предложил термин «предвзятая ретроспектива». В своей последней книге, «Все очевидно: когда вы знаете ответ» [39], социолог и пионер науки о сетях Дункан Ваттс предполагает, что и сказательное заблуждение, и предвзятая ретроспектива апеллируют к особому явлению, при котором люди, видящие необыкновенно успешные результаты, считают их за несомненный продукт упорной работы и таланта. Однако успех, в основном, возникает путём сложных и переплетённых шагов, каждый из которых зависит от предыдущих: если бы какой-то из них отличался, вся карьера или жизненный путь практически наверняка также оказались бы другими. Данный аргумент также основывается на результатах новаторского экспериментального исследования, проведённого несколькими годами ранее самим Ваттсом совместно с другими авторами [40], в котором успех ранее неизвестных песен на искусственном музыкальном рынке, как было показано, не коррелировал с качеством самого произведения. А это, несомненно, сильно затрудняет любые предсказания, что показано в другом, более свежем исследовании [41].

В данной работе, при помощи агентного статистического подхода, мы попробуем практически количественно определить роль удачи и таланта в успешных карьерах. В разделе 2, на основе минимального количества допущений, а именно Гауссова характера распределения таланта [42] и мультипликативных динамиках как успехов, так и неудач [43], мы представим простую модель, которую назвали моделью «Талант против Удачи» (ТпУ), в которой имитируется развитие профессиональных карьер группы людей на протяжении 40-летнего периода их работы. Модель показывает, что в реальности, случайность играет фундаментальную роль при определении наиболее успешных личностей. Истинным является то, что, как и можно было ожидать, талантливые люди вероятней станут богатыми, известными или значимыми в течение собственной жизни, по отношению с менее подготовленными. Но, и это менее интуитивное объяснение, обычным людям с заурядным уровнем таланта статистически предначертано становиться успешными (т.е. располагаться на конце какого-нибудь степенного распределения успешности) гораздо чаще, нежели самым талантливым, при условии, что они становились любимчиками фортуны на протяжении своей жизни. Этот факт встречается часто, как указано в ссылках [35, 36, 38], но, насколько нам известно, впервые смоделирован и измерен именно в данной работе.

Успешность людей с заурядным талантом ставит под вопрос «меритократическую» парадигму и все те стратегии и механизмы, которые давали больше вознаграждений, возможностей, чествования, славы и ресурсов людям, считающимся лучшими в их области [44, 45]. Дело в том, что, в подавляющем большинстве случаев, все оценки чьего-либо таланта давались постфактум, исключительно по взгляду на его / её деятельность, или достигнутые результаты, в какой-то конкретной области нашего общества, вроде спорта, бизнеса, финансов, искусства, науки и т.д. Такой вид вводящей в заблуждение оценки приводит к подмене причины и следствия, оценивая в качестве самых талантливых людей тех, кто, попросту, наиболее удачливы [46, 47]. В соответствии с этим взглядом, в предыдущих работах предупреждалось о подобных видах «недалёкой меритократии» и показалась эффективность иных стратегий, основанных на случайных выборках во множестве различных сред, таких как менеджмент, политика и финансы [48, 49, 50, 51, 52, 53, 54, 55]. В разделе 3 мы применяем наш подход и делаем наброски по сравнению возможных схем распределения общественных средств в контексте научного исследования. Мы изучаем последствия различных стратегий распределения, среди которых есть и «недалёко» меритократичная, с целью исследования новых способов повышения, одновременно, минимального уровня успешности наиболее талантливых людей общества и итоговой эффективности государственных расходов. Мы также исследуем, в общем, как предлагаемые средой возможности, представленные в виде уровней образования и дохода (т.е., внешних факторов, зависящих от страны и социального слоя, из которого происходят люди), имеют значение в повышении вероятности успеха. Завершают работу финальные замечания.

2. Модель

Далее мы предлагаем агентную модель, названую «Талант против Удачи» (ТпУ), основывающуюся на небольшом количестве допущений, и преследующую цель описать эволюцию карьер группы людей под влиянием случайно происходящих удачных и неудачных событий.

Рисунок 1: Пример исходных параметров для нашей симуляции. Все симуляции, представленные в данной работе, были проведены в агентной среде моделирования NetLogo [56]. N = 1000 людей (агентов), с различной степенью таланта (интеллект, навыки и т.д.), случайным образом распределённых по фиксированным позициям внутри квадратного мира из 201×201 участков с условиями цикличных границ. Во время каждой симуляции, которая охватывает несколько десятков лет, они подвергаются воздействию определённого количества N_E удачных (зелёные кружки) и неудачных (красные кружки) событий, перемещающихся по всему миру по случайным траекториям (случайное блуждание). В данном примере N_E = 500.

Мы рассматриваем N индивидов, с талантом T_i (интеллект, навыки, способности и т.д.), имеющим нормальное распределение в интервале [0; 1] вокруг данного среднего m_T со стандартным отклонением σ_T, случайным образом расставленных по фиксированным позициям внутри квадратного мира (см. рисунок 1) с условиями цикличности границ (т.е. с тороидальной топологией) и окруженных определённым количеством N_E «передвигающихся» событий (отмеченных точками), какие-то из которых удачные, другое нет (нейтральные события в данной модели не учтены, так как они не имеют никаких существенных последствий на жизнь индивидуума). На рисунке 1 мы показали данные события в виде цветных точек: удачные зеленым и с относительным процентом p_L, а неудачные красным и с процентом (100 − p_L). Общее количество событийных точек N_E распределено равномерно, но, разумеется, подобное распределение будет идеально однородным только для N_E → ∞. В наших симуляциях обычно будет N_E ≈ N/2, поэтому в начале каждой симуляции имеет место случайная значительная концентрация удачных или неудачных событийных точек в различных областях мира, в то время как другие области окажутся более нейтральными. Последующее случайное перемещение точек внутри квадратной матрицы, т.е., мира, не меняют данной фундаментальной особенности модели, что показывает на различное количество событий удачи или неудачи для разных людей на протяжении их жизни, не зависящее от их личного таланта.

Рисунок 2: нормальное распределение таланта среди популяции (с медианой m_T = 0,6, показанной прерывистой вертикальной линией, и стандартным отклонением σ_T = 0,1 – значения m_T ± σ_T отображены в виде двух точечных вертикальных линий). Данное распределение выделено в интервале [0; 1] и не меняется на протяжении симуляции.

В одной прогонке симуляции рассматривается период трудовой жизни P, равный 40 годам (в возрасте от двадцати до шестидесяти лет), с временным шагом δ_t, равным шести месяцам. В начале симуляции всем агентам выдан одинаковый капитал C_i = C(0) Ɐ_i = 1, …, N, представляющий их стартовый уровень успешности / благосостояния. Данный выбор преследует очевидную цель не дать никому первоначального преимущества. В то время как таланты агентов не зависят от времени, их капитал меняется. Во время развития данной модели, т.е., в течение предполагаемого периода жизни агентов, все событийные точки случайным образом передвигаются по миру и, при этом, возможно, пересекаются с местоположением каких-то агентов. Если вдаваться в подробности, то всякий раз каждая событийная точка покрывает, в случайном направлении, расстояние из 2 участков. Мы считаем, что происходит пересечение с индивидом, если событийная точка, представленная внутри круга с радиусом в один участок, центром находится на агенте (событийные точки после пересечения не исчезают). В зависимости от такого происшествия, в данном временном шаге t (т.е., каждые шесть месяцев), с определённым агентом A_k возможны три следующих варианта действий:

Никакая событийная точка не пересекает позицию агента A_k – это означает, что в течение последних шести месяцев не происходило подобных событий, агент A_k не выполняет никакого действия.
Позицию агента Ak пересекает удачное событие – это значит, что за последние шесть месяцев случилось удачное событие (обратите внимание, в соответствии со ссылкой [30], генерация инновационной идей здесь также считается удачным событием, случившимся в мозгу агента); как следствие, агент A_k удваивает свои капитал / успешность с вероятностью, пропорциональной его таланту T_k. Увеличение будет C_k(t) = 2C_k(t − 1), но только если rand[0; 1] < T_k, т.е., если агент достаточно умен, чтобы получить выгоду от подвернувшейся удачи.
Неудачное событие пересекает позицию агента A_k – это означает, что в течение последних шести месяцев произошло неудачное событие; как следствие, агент A_k теряет половину своих капитала / успешности, т.е. C_k(t) = C_k(t − 1) / 2.

Приведённые выше правила для агентов (включая выбор деления изначального капитала пополам в случае неудачных событий и удвоения при удачных, пропорционально таланту агента), намеренно просты и могут считаться широко распространёнными, так как как они основаны на очевидном факте, что успех в повседневной жизни имеет свойство как расти, так и снижаться в стремительном темпе. Более того, данные правила дают значительное преимущество высокоталантливым людям, так как те могут извлечь больше выгоды из возможностей, представляемых удачей (включая способность использовать хорошую идею, зародившуюся в их мозгах). С другой стороны, к примеру, автомобильная катастрофа или внезапная болезнь, всегда являются неудачными событиями, в которых талант не имеет значения. В этой связи, мы можем вывести более точное определение «таланта», определив его как «любое личное качество, которое повышает шанс ухватиться за возможность». Иными словами, под термином «талант» мы, в широком смысле, подразумеваем интеллект, навыки, находчивость, упорство, решимость, трудолюбие, принятие рисков и так далее. Далее мы увидим, что преимущество наличия великого таланта является обязательным, но недостаточным условием достижения очень высоких вершин успеха.

2.1. Результаты одной прогонки

В данном подразделе мы привели результаты прогонки одной типичной симуляции. Вообще говоря, эти результаты довольно устойчивы, поэтому, как мы покажем далее, их можно считать в значительной степени репрезентативными для общих рамок, выходящих из нашей модели.

Давайте представим N = 1000 агентов с равным количеством начального капитала C(0) = 10 (в абстрактных единицах) и с фиксированным талантом T_i ϵ [0; 1], следующим нормальному распределению со медианой m_T = 0,6 и стандартным отклонением σ_T = 0,1 (см. рисунок 2). Как было сказано ранее, симуляция охватывает реалистичный отрезок времени P = 40 лет, развиваясь равными шагами, по шесть месяцев каждый, всего из I = 80 итераций. В данной симуляции мы взяли N_E = 500 событийных точек, с вероятностью наступления удачных событий p_L = 50%.

По окончании симуляции, как видно из схемы (а) рисунка 3, мы выяснили, что простые динамические правила модели способны произвести неравноценное распределение капитала / успешности, с большим количеством бедных (неудачливых) агентов и малым числом крайне богатых (успешных). Построив то же распределение в билогарифмическом масштабе, на схеме (b) этого же рисунка видим распределение по степенной функции в духе Парето, наклон которой соответствует функции y© ≈ C^−1,27.

Таким образом, несмотря на нормальное распределение таланта, модель ТпУ, похоже, смогла ухватить первую важную особенность, наблюдаемую при сравнении с реальными данными: имеющийся глубочайший разрыв между богатыми и бедными и неизменную природу его масштаба. В частности, в нашей симуляции только 4 индивида получили более 500 единиц капитала, а 20 самых успешных людей владеют 44% всех ценностей, в то время как почти у половины популяции осталось менее 10 единиц. В целом, соблюдается правило Парето «80/20», так как у 80% популяции во владении находится лишь 20% всего капитала, в то время как оставшимся 20% индивидов досталось 80% богатств. Хотя данное неравенство, несомненно, выглядит несправедливым, было бы в некоторой степени приемлемым, если большинство преуспевших людей оказались из числа самых талантливых, таким образом заслужив накопления большего капитала / успешности, по сравнению с остальными. Но так ли происходит на самом деле?

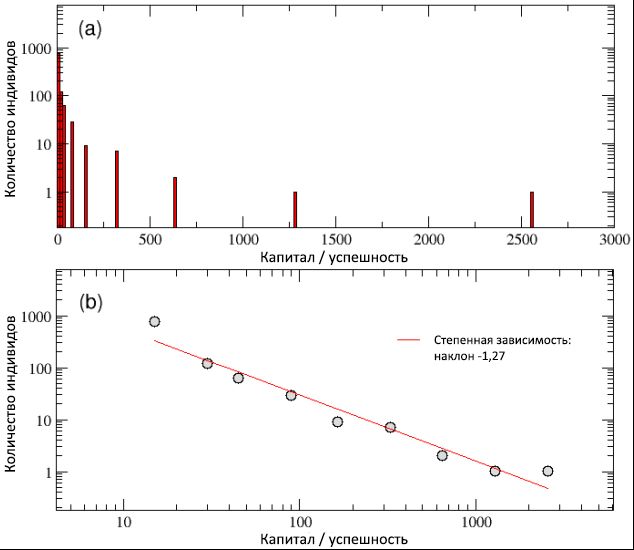
Рисунок 3: итоговое распределение богатств / успешности среди популяции, в логарифмически линейном (a) и билогарифмическом (b) масштабах. Несмотря на нормальное распределение таланта, хвост распределения успешности — как видно из схемы (b) — может быть описан в виде кривой степенной зависимости с наклоном −1,27. Мы также подтвердили, что распределение капитала / успешности следует закону Парето «80/20», так как 20% популяции владеет 80% ценностей и наоборот.

На рисунке 4, схемах (a) и (b), соответственно, отображены талант в виде функции от итоговых капитала / успешности, и наоборот (обратите внимание, что на схеме (a) капитал / успешность имеет только дискретные значения – это связано с решением использовать одинаковый для всех агентов начальный капитал). При взгляде на обе схемы видно, что, с одной стороны, наиболее успешные индивиды не являются самыми талантливыми и, наоборот, наиболее одаренные личности не являются самыми преуспевающими. В частности, наиболее успешный индивид, с C_max = 2560, обладает талантом T* = 0,61, что лишь немногим выше медианного значения m_T = 0,6, в то время как самый одарённый (T_max = 0,89) имеет капитал / успешность меньше, чем 1 единицу (C = 0,625).

Как мы подробней узнаем из следующего подраздела, такой результат является не частным случаем, а, скорее, правилом для систем подобного типа: максимальный успех никогда не сходится с максимальным талантом, и наоборот. Более того, такое расхождение между успехом и талантом является непропорциональным и в высокой степени нелинейным. Фактически, средний капитал всех людей с талантом T > T* имеет значение C ≈ 20; другими словами, капитал / успешность наиболее преуспевающих людей с умеренными талантами в 128 раз выше, чем средние капитал / успешность людей, являющихся гораздо более одарёнными, чем первые. Мы можем заключить, что если за причиной огромного успеха некоторых людей не скрыт исключительный талант, то, возможно, имеет место другой фактор. Наша симуляция ясно показывает, что таким фактором является чистое везение.

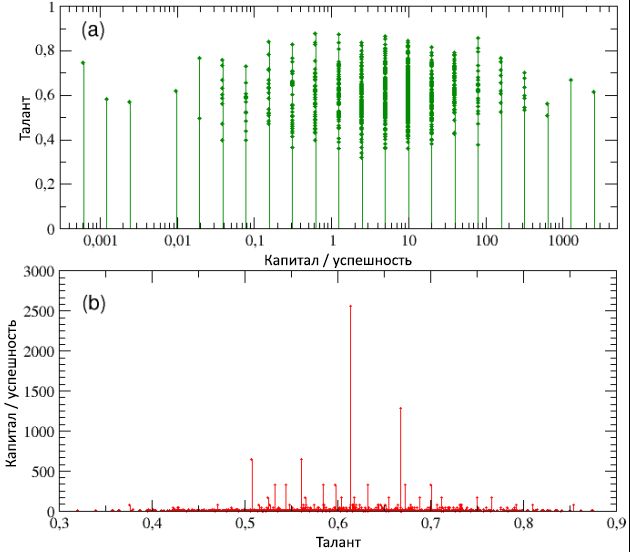
Рисунок 4: на схеме (а) талант отображён как функция капитала / успешности (в логарифмическом масштабе, для лучшей наглядности) – она свидетельствует, что самые успешные личности не являются, одновременно, и наиболее талантливыми. На схеме (b), наоборот, капитал / успешность показаны в виде функции от таланта – тут можно лучше оценить факт, что самый успешный агент, с C_max = 2560, обладает талантом, лишь слегка превышающим медианное значение m_T = 0,6, в то время как самый одарённый имеет капитал / успешность ниже, чем C = 1 единице, гораздо меньше начального капитала C(0). Читайте далее для получения более подробной информации.

На рисунке 5 количество удачных и неудачных событий, произошедших со всеми людьми за период их рабочей жизни, показано в виде функции от их итоговых капитала / успешности. При рассмотрении схемы (a) становится очевидно, что самые успешные личности одновременно являются и наиболее удачливыми (обратите внимание, что на данной схеме приведены все удачные события, случившиеся с агентами, а не только те, из которых они смогли извлечь выгоду, в соответствии со своим талантом). Напротив, при взгляде на схему (b), видим, что самые неуспешные одновременно являются и наиболее неудачливыми. Другими словами, хотя корреляция между успехом и талантом, исходя из симуляций, отсутствует, зато имеется сильная зависимость успеха от удачи. Анализируя подробности распределений частот количества происходивших с индивидами удачных и неудачных событий, мы обнаружили, как это показано на схемах © и (d), что оба этих значения экспоненциальные, со степенями 0,64 и 0,48, а медианами 1,35 и 1,66, соответственно, и что максимальные количества произошедших удачных и неудачных событий были, соответственно, 10 и 15. Более того, у примерно 16% была «нейтральная» жизнь, вообще без удачных и неудачных событий, в то время как 40% индивидов сталкивались исключительно с каким-то одним типом событий (удачным или неудачным).

Также интересно взглянуть на период развития успешности / капитала как у наиболее удачливых личностей, так и для самых неуспешных, сравнив с соответствующими последовательностями удачных и неудачных событий, произошедшими в течение 40 лет (80 интервалов, по 6 месяцев каждый) их трудовой жизни. Результаты можно увидеть, соответственно, в левой и правой частях рисунка 6. В отличие от схемы (a) с изображения 5, нижние схемы данного рисунка содержат лишь те удачные события, из которых агенты, благодаря своему таланту, смогли извлечь выгоду.

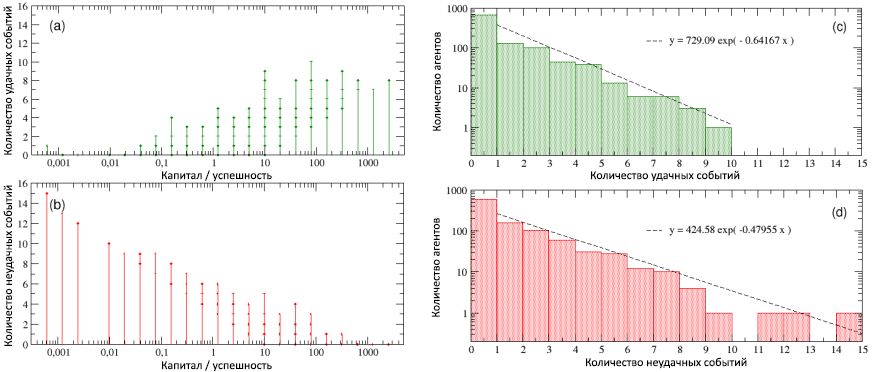
Рисунок 5: общее число удачных (a) и неудачных (b) событий, в виде функций от капитала / успешности агентов. График показывает наличие сильной корреляции между успешностью и удачей: самые успешные личности также являются наиболее удачливыми, и наоборот. Опять же, из-за использования одинакового для всех агентов начального капитала, получается, что ряд событий сгруппирован в дискретных значениях капитала / успешности. На схемах © и (d) частота распределений, соответственно, количества удачных и неудачных событий отображена в логлинейном масштабе. Как видно, оба распределения могут быть записаны в виде экспоненциальных зависимостей с похожими отрицательными степенями).

На (верхней и нижней) схемах (a) рисунка 6, касающихся умеренно талантливого, но наиболее успешного индивида, ясно видно, что после примерно половины его трудовой жизни, сопровождавшейся редким проявлением удачных событий (нижняя схема), и низким же уровнем капитала (верхняя схема), внезапная концентрация благоприятных событий, случившаяся между 30 и 40 временными шагами (т.е. прямо перед 40-летием агента) привела к стремительному росту капитала, который на последних 10 шагах (т.е., в последние 5 лет карьеры агента) стал экспоненциальным, перейдя от C = 320 до C_max = 2560.

С другой стороны, посмотрев на (верхнюю и нижнюю) схемы (b) того же рисунка, касающиеся наименее удачливого индивида, становится очевидно, что особо неудачная вторая половина его трудовой жизни, сопровождающаяся десятком неблагоприятных событий, постоянно снижала капитал / успешность, приведя к финальному значению C = 0,00061. Интересно отметить, что талант данного несчастного агента был T = 0,74, что выше, чем у большинства самых успешных. Очевидно, на создание различий повлияла удача. И, если справедливо то, что самый удачливый агент заслуживал получения выгоды ото всех предоставленных ему возможностей (несмотря на свой посредственный талант), также верно и то, что если ваша жизнь полна несчастий и не даёт возможностей, как у этого второго агента, то даже величайший талант становится бессильным против неистовой неудачи.

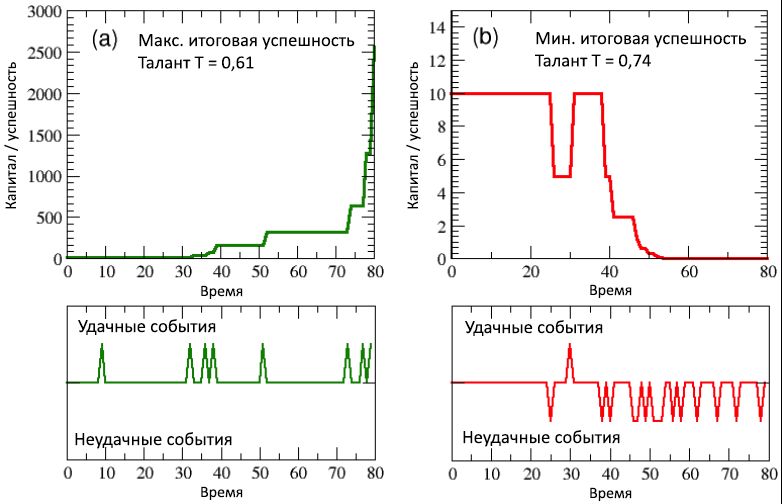
Рисунок 6: (a) период развития успешности / капитала наиболее успешного индивида и (b) самого неудачливого, сопоставленных по соответствующим последовательностям удачных и неудачных событий, произошедших в течение их трудовой жизни (из 80 полугодий, т.е., 40 лет). Время происхождения таких событий отмечено на нижних схемах, в виде восходящих и нисходящих пиков.

Все результаты одиночной прогонки (демо-версию кода NetLogo модели ТпУ, использованного для этой симуляции, можно найти в репозитории Open ABM), приведённые в данном подразделе, весьма устойчивы и, как мы увидим из следующего подраздела, они сохраняются, с незначительными отличиями, при множестве повторов симуляций, начинающихся с таким же распределением таланта, но разными случайными позициями индивидов.

2.2. Результаты множества прогонок

В данном подразделе мы представили общие результаты симуляции из, в среднем, более 100 прогонок, каждая начиналась с разными, выбранными случайным образом, исходными условиями. Значения управляющих параметров были те же, что и в предыдущем подразделе: N = 1000 индивидов, m_T = 0,6 и σ_T = 0,1 для нормального распределения таланта, I = 80 итераций (каждая представляет δ_t = 6 месяцев трудовой жизни), C(0) = 10 единиц начального капитала, N_E = 500 событийных точек и процент удачных событий p_L = 50%.

На схеме (a) рисунка 7 общее распределение итогового капитала / успешности среди всех агентов, собранное в результате 100 прогонок, показано в билогарифмическом масштабе и оно хорошо описывается кривой степенной зависимости с угловым коэффициентом −1,33. Наблюдавшееся в одиночной прогонке свойство постоянности капитала безотносительно масштаба и следующее из него высокое неравенство среди индивидов, также как и правило Парето «80/20», таким образом, сохранились и в случае множественных прогонок. В действительности, разрыв между богатыми (успешными) и бедными (неудачливыми) агентами даже вырос, поскольку капитал наиболее богатых людей теперь превысил 40000 единиц.

Этот результат лучше всего можно оценить, взглянув на схему (b) рисунка 7, где в виде функции от таланта приведён итоговый капитал C_max только наиболее успешных индивидов, т.е. показавших лучший результат в каждой из 100 прогонок. Больше всего очков получил агент с талантом T_best = 0,6048, практически совпадающим с медианой распределения таланта (m_T = 0,6), который достиг пикового капитала C_best = 40960. С другой стороны, самый одарённый из наиболее успешных индивидов, с талантом T_max = 0,91, набрал капитал C_max = 2560, составляющий лишь 6% от C_best.

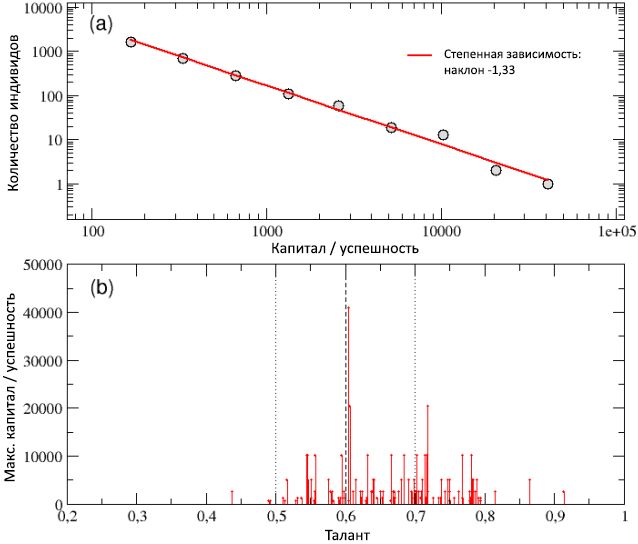
Рисунок 7: схема (a) – распределение итогового капитала / успешности, рассчитанного за 100 прогонок, для популяций, обладающими различными случайно определёнными первоначальными условиями. Распределение можно описать кривой степенной зависимости с наклоном −1,33. Схема (b) – итоговый капитал C_max наиболее успешных личностей в каждой из 100 прогонок, показанный в виде функции от их таланта. Люди с умеренно-высоким талантом, в среднем, оказываются успешней тех, у кого талант низкий или умеренно-низкий, при этом чаще всего самый успешный индивид – это умеренно одарённый агент, и лишь изредка – самый талантливый. Значение m_T, а также значения m_T ± σ_T, показаны, соответственно, в виде вертикальных прерывистой и точечной линий.

С целью более подробного рассмотрения данной точки зрения, на рисунке 8 (а) мы построили график распределения таланта лучших исполнителей, подсчитанных за 100 прогонок. Распределение, очевидно, смещено вправо по оси таланта, со средним значением T_av = 0,66 > m_T – это подтверждает, с одной стороны, что для достижения значительного успеха зачастую необходим умеренно-высокий талант; однако, с другой стороны, также показывает, что этого условия практически никогда не достаточно, так как агенты с наивысшим талантом (т.е., с T > m_T = 2σ_T, или T > 0,8) оказываются среди лучших исполнителей лишь в 3% случаев, а их капитал / успешность никогда не превышает 13% от C_best.

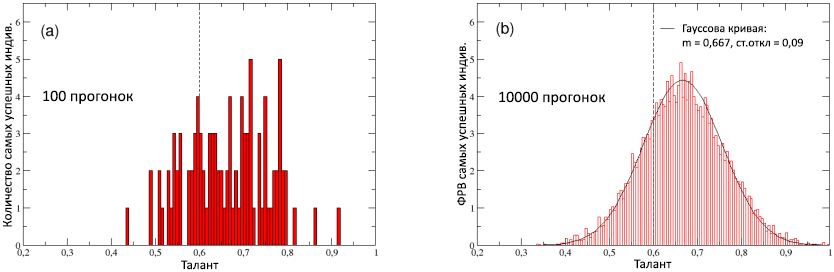
Рисунок 8: (a) Распределение таланта наиболее удачливых личностей (лучшие исполнители) в каждой из 100 прогонок. (b) Функция распределения вероятности (ФРВ) таланта самых успешных индивидов, рассчитанная в 10000 прогонок: хорошо описывается нормальным распределением с медианой 0,667 и стандартным отклонением 0,09 (сплошная кривая). Для сравнения приведена медиана m_T = 0,6 исходного нормального распределения таланта в популяции, показанная на обеих схемах прерывистой вертикальной линией.

На схеме (b) рисунка 8 то же распределение (приведённое к общей площади, чтобы получить ФРП) подсчитано для 10000 прогонок, с целью понимания его истинной формы: похоже, что оно укладывается в Гауссову кривую G(T) со средним T_av = 0,667 и стандартным отклонением 0,09 (сплошная линия). Это, безусловно, подтверждает, что распределение таланта лучших исполнителей смещено вправо относительно оси таланта, по сравнению с исходным распределением. Если быть точней, это означает, что условная вероятность P(C_max|T) = G(T)dT найти среди лучших исполнителей личность с талантом в интервале [T; T + dT] растет с талантом T, достигает максимума возле, примерно, умеренно-среднего таланта T_av = 0,66, а затем резко падает при больших значениях таланта. Другими словами, вероятность обнаружить на вершине успеха умеренно талантливого индивида выше, чем найти там же высокоодарённого. Заметьте, что в идеальном мире, в котором талант являлся главной причиной успеха, ожидается, что P(C_max|T) будет растущей функцией от T. Таким образом, мы можем заключить, что наблюдаемая гауссова форма P(C_max|T) является доказательством большего значения удачи, нежели таланта, в достижении крайне высоких уровней успешности.

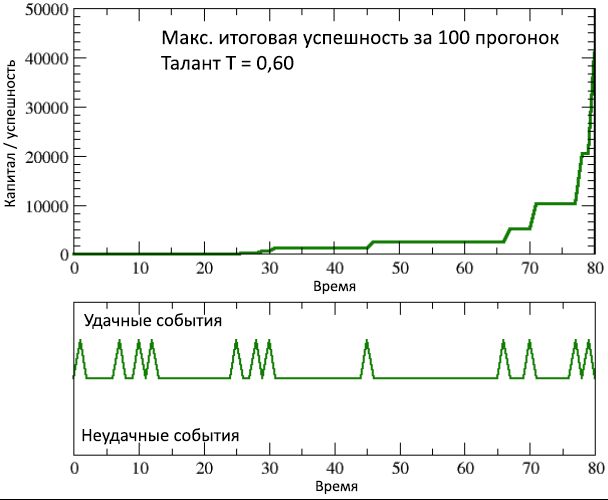
Рисунок 9: изменение во времени успешности / капитала наиболее успешной личности (но, при этом, умеренно одарённой), из 100 прогонок симуляции, сопоставленное с соответствующей необычной последовательностью удачных событий, случившихся в её жизни.

Также интересно сравнить из 100 прогонок средние капитал / успешность C_mt ≈ 63 наиболее талантливых людей с соответствующим средним C_at ≈ 33 тех, чей талант близок к медиане m_T. В обоих случаях мы обнаружили довольно низкие показатели (пусть и больше начального капитала C(0) = 10), но тот факт, что C_mt > C_at, указывает на то, что, хотя вероятность обнаружить умеренно талантливого индивида на вершине успеха выше, чем того, который высоко одарён, самые талантливые личности каждой прогонки, в среднем, более успешны, чем умеренно одарённые люди. С другой стороны, взглянув на среднюю по 100 прогонкам долю индивидов с талантом T > 0,7 (т.е. выше, чем со стандартным отклонением от медианы) и итоговыми успешностью / капиталом C_end > 10, подсчитанными с учётом всех агентов, обладающих талантом T > 0,7 (которых, в среднем для каждой прогонки, ≈ 160), мы обнаружили, что данная доля равна 32% – это значит, что совокупная результативность наиболее талантливых людей нашей популяции, в среднем, относительно невелика, так как лишь треть из них достигают итогового капитала, превышающего изначальный.

В любом случае, неопровержим факт, что лучший исполнитель среди 100 прогонок симуляции – это агент с талантом T_best = 0,6, идеально совпадающим с медианой, и с итоговым успехом C_best = 40960, что в 650 раз больше, чем C_mt, и в более чем 4000 раз выше, чем успешность C_end < 10 у 2/3 самых талантливых людей. Это произошло, в итоге, просто лишь потому, что он оказался удачливей остальных. Безусловный везунчик, как это видно из рисунка 9, где приведены рост его капитала / успешности на протяжении трудовой жизни, наряду со впечатляющей чередой удачных (и только удачных) событий, из которых, несмотря на недостаток исключительности таланта, он смог получать выгоду в течение своей карьеры. Подытоживая, к данному моменту было обнаружено, что, несмотря на свою простоту, модель ТпУ, похоже, способна учитывать многие особенности, характеризующие, как было сказано во введении, высокое неравенство распределения богатства и успешности в нашем обществе, очевидно контрастирующее с Гауссовым распределением таланта среди людей. Также модель в количественном виде показывает, что большого таланта недостаточно для гарантированно успешной карьеры и что, напротив, менее одарённые люди крайне часто достигают вершины успеха – это ещё один «условный факт», часто наблюдаемый в реальной жизни [35, 36, 38]. Ключевой аспект, который интуитивно объясняет, как может произойти такое, что умеренно одарённые личности достигают (настолько часто) гораздо больших чести и успеха, в сравнении с более талантливыми, заключается в том, что имеет место скрытая и часто недооцениваемая роль удачи, как это наглядно видно из наших симуляций. Но для понимания истинного значения результатов наших исследований важно различать макро от микро точки зрения. По сути, на микро-уровне, следуя динамическим правилам модели ТпУ, одарённый индивид обладает априори большей вероятностью достижения высокого уровня успешности, по сравнению с умеренно талантливым, так как у него выше способность ухватиться за появляющуюся возможность. Таким образом, с точки зрения отдельного индивида, нам следует заключить, что, не имея возможности (по определению) влиять на появление удачных событий, лучшей стратегией по увеличению вероятности достижения успешности (при любом уровне таланта) является расширение личной активности, генерирование идей, коммуникации с другими людьми, поиск разнообразия и взаимообогащения. Другими словами, становление личностью с широким кругозором, готовой контактировать с другими, даёт наивысшую вероятность удачного события (которое будет реализовано в меру таланта личности). С другой стороны, на макро-уровне, с точки зрения всего общества, вероятность встретить на вершинах успеха умеренно одарённых личностей гораздо выше, чем обнаружить там же крайне талантливых, потому что первых гораздо больше и, благодаря удаче, они обладают, в общем, статистическим преимуществом достичь грандиозного успеха, несмотря на собственную априори более низкую личную вероятность. В следующем разделе мы рассмотрим данную макро-уровневую точку зрения, исследовав возможности, предложенные нашей моделью, чтобы подробно изучить более эффективные стратегии и политики по улучшению среднего уровня результативности наиболее талантливых людей популяции, реализующие более продуктивные способы распространения наград и ресурсов. Фактически, мы ожидаем, что любая политика, способная повысить уровень наиболее талантливых личностей, которые являются двигателем прогресса и инновацией нашего общества, будет иметь совокупно благотворное влияние.

3. Эффективные стратегии по уравновешиванию удачи

Приведённые в предыдущем разделе результаты явно согласуются с подтверждёнными документально эмпирическими свидетельствами, рассмотренными во введении, что ставит под вопрос недалёко меритократическое предположение, утверждающее, что естественные различия в таланте, навыках, способностях, интеллекте, трудолюбии или упорстве являются единственными причинами успеха. Как мы показали, удача также имеет влияние и может сыграть крайне важную роль. Суть обсуждения в том, что, в силу трудноизмеримости (во многих случаях сложно определить в точных выражениях) личных качеств, для распределения чествования, финансирования или наград применяются меритократические стратегии, зачастую основанные на частных результатах, оцененных в показателях личного богатства или успеха. В результате, такие стратегии влияют на дальнейшее действие по укреплению и подкачивают богатство / успешность наиболее удачливых личностей за счёт механизма положительной обратной связи, который походит на процесс «богатые богатеют» (также известный как «эффект Матфея» [57, 58, 59]), с несправедливым итоговым результатом.

Давайте представим, например, финансируемый государством совет по научно-исследовательской деятельности, с фиксированным количеством денег в его распоряжении. Что будет намного эффективней для повышения средней результативности исследования: давать большие гранты лишь нескольким несомненно превосходным учёным или мелкие гранты множеству очевидно более заурядных научных работников? Недавнее исследование [44], основанное на анализе четырёх индексов научной значимости связанных публикаций, выявило, что значимость имеет лишь слабую положительную связь с финансированием. В частности, значимость на доллар была ниже для крупных обладателей грантов, а значимость от учёных, получавших повышения в финансировании не возросла в соответствующей степени. Авторы исследования пришли к выводу, что научная значимость (как отражено в публикации) лишь слабо граничит с финансированием, и предположили, что стратегии финансирования, нацеленные на диверсификацию идей, нежели на «превосходность», скорее всего окажутся более продуктивными. Более поздний вклад [60] показал, что, как в количестве произведённых документов, так и в их научной значимости, концентрированное финансирование исследований обычно приводит к уменьшающимся маржинальным доходностям, а также, что наиболее финансированные исследователи не выделяются в показателях результативности и научной значимости. Вообще, такие выводы не должны удивлять в свете другого последнего открытия [18], заявляющего, что значимость, будучи измеренной по влиятельным публикациям, случайным образом распределена по всему ряду публикаций учёного. Другими словами, удача имеет значение, и если она влияет больше, чем мы желаем того признать, не удивительно, что меритократические стратегии оказываются менее эффективными, чем ожидалось, в особенности, если мы пытаемся оценить заслугу апостериори. В предыдущих исследованиях [48, 49, 50, 51, 52, 53, 54, 55] уже имелось предупреждение против такого рода «недалёкой меритократии», показывающее эффективность альтернативных стратегий, основанных на случайных выборах в областях менеджмента, политики и финансов. Согласно такой точке зрения, модель ТпУ показывает, как может быть повышен минимальный уровень успешности для большинства талантливых людей в мире, где удача имеет значение, а случайное открытие часто приводит к важным достижениям.

3.1. Случайное открытие, инновация и эффективные стратегии финансирования

Термин «случайное открытие» широко используется в литературных ссылках на исторические факты, показывающие, что исследователи довольно часто совершают неожиданные и полезные открытия по чистой случайности, когда ищут что-то иное [61, 62]. Существует длинный список историй открытий, совершённых исключительно по счастливому стечению обстоятельств: от пенициллина Александром Флемингом до радиоактивности Марией Кюри, от космического микроволнового реликтового излучения радиоастрономами Арно Пензиасом и Робертом Вудро Вильсоном до графена Андреем Геймом и Константином Новосёловым. Приведём более свежий пример: сеть заполненных жидкостью каналов в человеческом теле, ранее неизвестный орган, который, видимо, способствует распространению раковых клеток, был открыт случайно, во время простой эндоскопии [63]. Поэтому многие считают, что следует всегда финансировать движимые любопытством исследования, так как никто на самом деле не может знать заранее или предсказать, к чему они способы привести [64].

Возможно ли количественно измерить значимость случайного открытия? Каковы наиболее эффективные способы симуляции случайного открытия? Оно способно принимать множество разных форм, и его сложно ограничить и выразить количественно. Вот почему до сих пор академические исследования рассматривали случайное научное открытие, по большей части, как на философское понятие. Но времена меняются. Европейский исследовательский совет недавно выделил биохимику Охиду Якубу грант в 1,7 миллиона долларов США на подсчёт значимости случайного открытия в науке [65]. Якуб обнаружил, что случайное открытие можно классифицировать по четырём базовым типам [66] и что могут существовать важные факторы, влияющие на его появление. Его выводы, видимо, совпадают с идеями, выработанными в более ранних изысканиях [67, 68, 69, 70, 71, 72], утверждающих, что общепринятым, явно меритократическим, стратегиям, которые преследуют превосходство и вытесняют разнообразие, похоже, предначертано быть проигрышными и неэффективными. Причина в том, что они априори отвергают исследования, изначально выглядящие менее обещающими, но которые, благодаря, в частности, случайному открытию, могли бы апостериори оказаться невероятно инновационными.

С этой точки зрения мы хотим применить модель ТпУ, естественным образом выражающую удачу (а, следовательно, и случайное открытие) как количественный параметр стратегии, с целью изучения в данном подразделе эффективности различных сценариев финансирования. В частности, в ситуациях, когда, как говорилось выше, умеренно-талантливый-но-удачливый человек зачастую более успешен, чем более-одарённые-но-невезучие индивиды, важно оценивать эффективность стратегий финансирования на способность сохранения минимального уровня успешности в том числе и для наиболее талантливых людей, которые, как ожидается, привнесут самые инновационные и прогрессивные идеи.

Начав с теми же исходными параметрами, что были использованы в подразделе 2.2, т.е. N = 1000, m_T = 0,6, σ_T = 0,1, I = 80, δ_t = 6, C(0) = 10, NE = 500, p_L = 50% и 100 прогонок симуляции, давайте представим, что имеющийся общий капитал финансирования F_T периодически распределяется среди индивидом по различным критериям. Например, финансы могут быть выданы:

Всем поровну (уравнительный критерий), чтобы поощрить исследовательское разнообразие;
Только определённому проценту наиболее успешных («лучших») индивидов (элитарный критерий), что ранее было названо «недалёкой» меритократией, за распределение финансов среди людей на основе прошлой результативности.
«Премиальным» распределением среди определённой доли наиболее успешных индивидов, а остатка, небольшими равными частями, по остальным (смешанный критерий);
Только определённому проценту индивидов, выбранных случайным образом (выборочный случайный критерий).

Мы реалистично предполагаем, что общий капитал F_T будет распределяться каждые 5 лет, в течение 40-летнего периода каждой прогонки симуляции, так что время от времени будет распределяться F_T = 8 единиц капитала. При помощи периодических вливаний этих финансов мы намереваемся поддерживать минимальный уровень ресурсов наиболее талантливых агентов. Таким образом, хорошим показателем эффективности выбранной стратегии финансирования может быть процент P_T, средний за 100 прогонок симуляции, у индивидов с талантом T > m_T + σ_T, чьи итоговые успешность / капитал превышают первоначальный уровень, т.е., C_end > C(0).

Данный процент уже был подсчитан во время прогонок симуляции, представленных в подразделе 2.2. Там показано, что при отсутствии финансирования, лучшая результативность достигнута наиболее удачливыми агентами с близким к среднему талантом, в то время как капитал / успешность самых талантливых людей всегда остаются крайне низкими. В частности, только лишь часть P_T0 ≈ 32% от общего числа агентов с талантом T > 0,7 смогла достичь, по итогу симуляции, капитала / успешности, превышающих начальное значение. Следовательно, для сравнения эффективности различных стратегий финансирования, должен быть подсчитан рост среднего процента P_T относительно P_T0 тех талантливых людей, которые в течение своей карьеры преумножили свой начальный капитал. Давайте определим данный рост как P^*_T = P_T − P_T0. Данная величина является довольно стабильным показателем: мы проверили его повторением из 100 симуляций, разброс значений P^*_T оставался ниже 2%. Наконец, если посчитать соотношение P^*_T к общему капиталу, распределённому по всем агентам в течение 40 лет, можем получить индекс эффективности E, который оценивает рост числа достаточно успешных талантливых людей на единицу инвестированного капитала, определяемый как E = P^*_T / F_T.

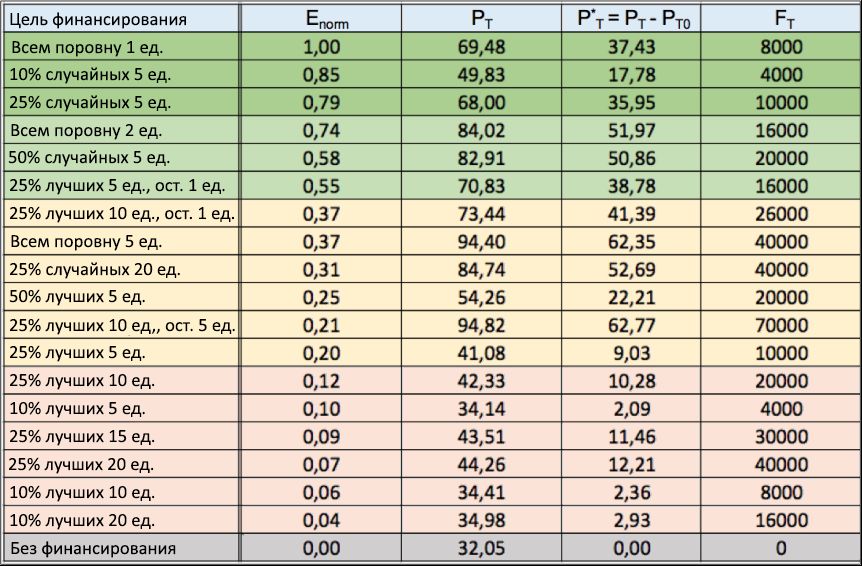
Рисунок 10: таблица стратегий финансирования. Приведены несколько стратегий распределения финансов по различным целям (1 столбец), с результатами нормализованного индекса эффективности E_norm (2 столбец), в убывающем порядке. Также, в третьем и четвёртом столбцах, соответственно, приведены значения доли P_T успешных талантливых людей и чистого роста их количества P^*_T, по отношению к сценарию «без финансирования», в среднем за 100 прогонок симуляции. Наконец, в последнем столбце показан общий капитал F_T, инвестированный в каждой прогонке.

В таблице, приведённой на рисунке 10, мы показали индекс эффективности (2-й столбец), полученный для нескольких стратегий распределения финансирования, каждая со своей финансовой целью (1 столбец), а также соответствующие значения P_T (3-й столбец) и P^*_T (4-й столбец). Там же, в последнем столбце, приведён суммарный для каждой прогонки инвестированный капитал F_T. Индекс эффективности E был нормализован относительно его максимального значения E_max, а все записи (строки) упорядочены по критерию уменьшения значений E_norm = E / E_max. Для сценария с отсутствием финансирования, по определению, E_norm = 0. Эти же результаты E_norm приведены как функция от принятых стратегий финансирования в форме гистограммы на рисунке 11. Благодаря статистической устойчивости P_T, показывающей отклонения менее 2%, приведённые результаты индекса эффективности E_norm отличаются стабильностью.

При рассмотрении приведённой выше таблицы и соответствующей ей гистограммы с рисунка 11, становится очевидно, что если целью является вознаграждение наиболее талантливых личностей (тем самым повышая их итоговый уровень успешности), то намного лучше выделять периодически (пусть даже небольшое) количество капитала всем индивидам сразу, нежели выдавать больший капитал только малой их части, отобранной по уровню успешности, достигнутому к моменту распределения.

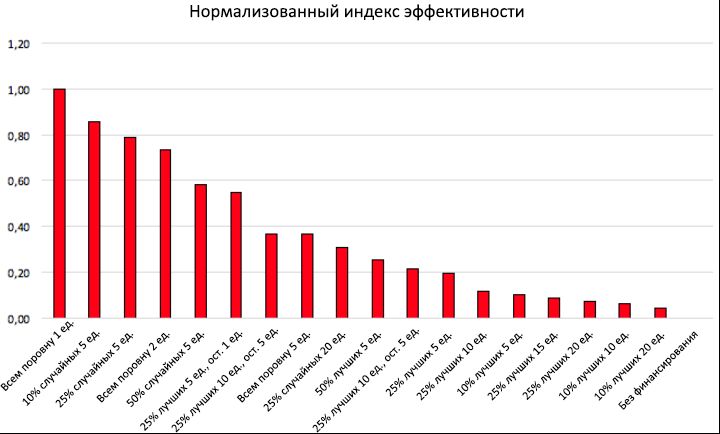
Рисунок 11: нормализованный индекс эффективности некоторых стратегий финансирования. Значения нормализованного индекса эффективности E_norm приведены в виде функции по различным стратегиям финансирования. На рисунке показано, что, для повышения успешности большего числа талантливых людей с C_end > C(0), гораздо эффективней распределять небольшие суммы финансов среди множества индивидов, нежели осуществлять финансирование другими, более выборочными способами.

С одной стороны, гистограмма показывает, что «уравнительный» критерий, выделяющий каждому индивиду 1 единицу капитала раз в 5 лет, является наиболее эффективным способом распределения финансов, с E_norm = 1 (т.е., E = E_max): при относительно небольших инвестициях F_T в размере 8000 единиц, получается удвоить процент успешных талантливых людей, по сравнению со сценарием «без финансирования», приводя его от P_T0 = 32,05% к P_T = 69,48%, с чистым ростом P^*_T = 37,43. При рассмотрении повышения общего инвестированного капитала (например, за счёт установки уравнительной квоты в размере 2 или 5 единиц), данная стратегия также обеспечивает дальнейший рост итогового процента успешных талантливых людей (с 69,48% до 94,40%), однако нормализованная эффективность при этом постепенно снижается, от E_norm = 1 до E_norm = 0,74, а затем до E_norm = 0,37, соответственно.

С другой стороны, «элитарные» стратегии, распределяющие каждые 5 лет по большой сумме финансов (5, 10, 15 или 20 единиц) только среди лучших 50%, 25% или даже 10% уже успешных индивидов, располагаются в самом низу таблицы, с E_norm < 0,25 во всех указанных сценариях, чистый рост P^*_T итогового числа успешных талантливых людей, в сравнении со сценарием «без финансирования», остаётся крайне низким (почти во всех случаях менее 20%), зачастую несмотря на гораздо больший инвестированный капитал, если сравнивать с подобной уравнительной стратегией. Данные результаты укрепляют предположение, что такой подход, очевидно, является недалёко меритократичным.

Стоит заметить, что принятие «смешанного» критерия, т.е. распределение «меритократичной» финансовой части среди определённого процента наиболее успешных индивидов, например, 25%, с раздачей оставшихся финансов в равных долях остальным людям, даёт лучшие, по сравнению с «недалёко меритократичным» подходом, результаты индекса эффективности. Однако, по продуктивности данная стратегия не способна догнать «уравнительный» критерий. Как это ясно видно, например, из сравнения шестой и четвёртой строчек таблицы финансирования: несмотря одинаковое общее инвестирование в размере 16000 единиц, значение P_T, полученное при смешанном критерии, остаётся намного ниже, чем при уравнительном подходе (70,83% против 84,02%), что также подтверждается соответствующими значениями индекса эффективности E_norm (0,55 против 0,74).

Если учесть психологические факторы (не смоделированные в данном исследовании), то смешанная стратегия может быть заново пересмотрена в сравнении с уравнительной. В действительности, премиальное вознаграждение, назначенное самым успешным индивидам, может стимулировать большую приверженность у всех агентов, тогда как распределённая поровну оставшаяся часть сыграет двоякую роль: на индивидуальном уровне она будет стимулировать разнообразие и предоставление неудачливым талантливым людям новых шансов на реализацию своего потенциала, а на общем уровне будет поддерживать случайные открытия, тем самым способствуя развитию исследований и сообщества в целом.

Снова взглянув на таблицу стратегий финансирования, стоит обратить внимание на невероятно высокую эффективность случайных стратегий, которые занимают две из трёх лучших позиций в общем результате. Отсюда вытекает, что, к примеру, периодическое вознаграждение в 5 единиц только 10% случайно выбранных индивидов, с общей суммой инвестиций всего лишь в 4000 единиц, даёт чистый рост P^*_T = 17,78%, что выше практически всех полученных при помощи уравнительных стратегий. Более того, повышение до 25% доли случайно финансируемых людей и удвоение общих инвестиций (подняв их до 10000 единиц) даёт чистый рост P^*_T = 35,95, сравнимый с тем, что получен лучшей уравнительной стратегией, занявшей первое место в общем зачёте. Бросается в глаза, что этот последний результат P^*_T примерно в четыре раза больше значения (P^*_T = 9,03%), полученного при элитарном подходе (см. 12 строку таблицы), распределившем точно такой же капитал (10000 единиц) среди того же числа индивидов (25% от общего количества). Последнее ещё больше подтверждает, что в сложных социальных и экономических средах, где шанс играет значительную роль, эффективность иных стратегий, основанных на случайных выборах, легко может обойти стандартные, базирующиеся на «недалёком меритократичном» подходе, стратегии. Данный, противоречащий здравому смыслу, феномен, уже наблюдавшийся в сферах менеджмента, политики и финансов [48, 49, 50, 51, 52, 53, 54, 55], находит, таким образом, очередное подтверждение и в контексте исследования финансирования.

С целью дополнительного подтверждения полученных данных, на рисунке 12 приведены результаты ещё одной серии симуляций. В отличие от предыдущих симуляций, здесь общая сумма инвестированного в каждой из 100 прогонок капитала теперь фиксирована в значении F_T = 80000, так что среди агентов каждые 5 лет распределяется F_T/8 = 10000 единиц, по тем же, рассмотренным ранее, стратегиям финансирования. Взглянув на таблицу, видим, что результаты уравнительной стратегии снова оказались самыми эффективными в плане вознаграждения наиболее талантливых людей, с долей P_T близкой к 100%. Следом идёт случайная стратегия (с 50% случайно выбранных для финансирования индивидов), а затем смешанная, в которой половина капитала распределена среди 25% наиболее успешных индивидов, а другая часть, равными долями, среди остальных людей. Напротив, все элитарные стратегии снова расположились в конце рейтинга, тем самым ещё больше подтверждая неэффективность «недалёко меритократичного» подхода в награждении истинного таланта.

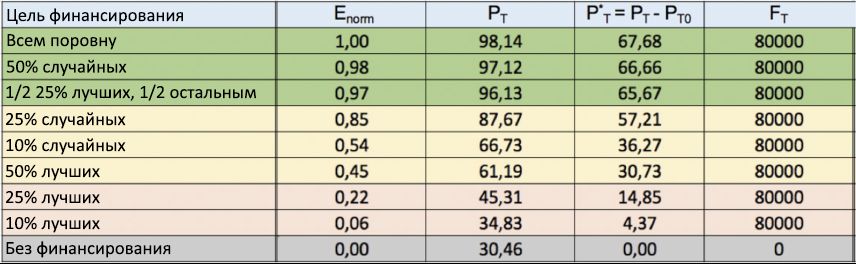
Рисунок 12: таблица стратегий финансирования с фиксированными финансами. Полученные нормализованные индексы эффективности E_norm для нескольких стратегий распределения финансирования (1-й столбец) снова приведены в убывающем порядке, сверху вниз. В отличие от рисунка 10, здесь общий инвестированный в каждой прогонке капитал зафиксирован на F_T = 80000. Уравнительная стратегия снова заняла первое место.

Результаты симуляций модели ТпУ, представленные в данном подразделе, заострили внимание на значимости внешних факторов (как, впрочем, и эффективных политик финансирования) в повышении возможностей успеха большинства талантливых индивидов, слишком часто оказывающихся наказанными по стечению неудачных событий. В следующем подразделе мы исследуем до какой степени новые возможности должны исходить из перемен в окружении, например, таких как уровень образованности или иных стимулов, получаемых из социальной среды, в которой живут или откуда приходят люди.

3.2. Значимость окружения

Для начала, позвольте нам оценить роль среднего уровня образованности у населения. В рамках модели ТпУ его можно получить путём изменения параметров нормального распределения таланта. Вообще, если предположить, что талант и навыки индивидов, при их стимулировании, могут оказаться более эффективными в реализации новых возможностей, то повышение или медианы m_T, или стандартного отклонения таланта σ_T может быть интерпретировано как последствие политик, нацеленных, соответственно, либо на поднятие среднего уровня образованности, либо на усиление учебной подготовки наиболее одарённых людей.

На двух схемах рисунка 13 мы привели итоговые капитал / успешность, накопленные лучшими исполнителями каждой из 100 прогонок, в виде функции от их таланта. Заданные параметры соответствуют тем, что были использованы в подразделе 2.2 (N = 1000, I = 80, δ_t = 6, C(0) = 10, N_E = 500 и p_L = 50%), но с различными моментами распределения талантов. В частности, на схеме (a) мы оставили неизменённым m_T = 0,6, но повысили σ_T = 0,2, в то время как на схеме (b) сделали противоположное, оставив σ_T = 0,1 и подняв m_T = 0,7. В обоих случаях можно заметить смещение вправо пиков максимального успеха, но с различием в деталях.

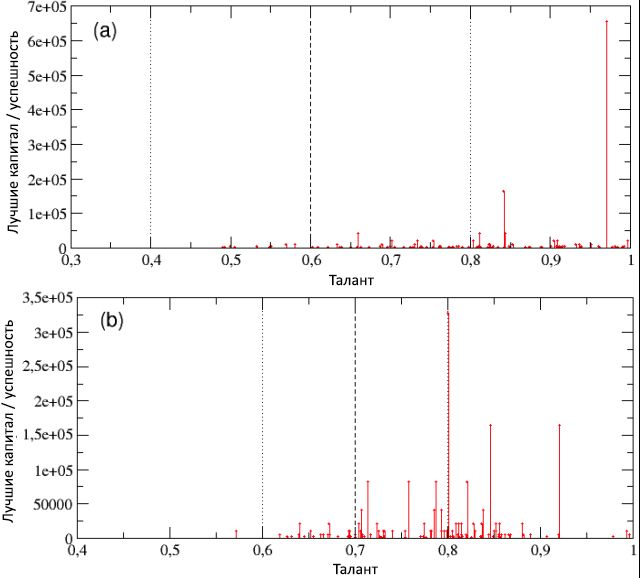
Рисунок 13: итоговый капитал наиболее успешных индивидов в каждой из 100 прогонок, представленный в виде функции от их таланта для популяций с различными параметрами распределений таланта: (a) m_T = 0,6 и σ_T = 0,2 (что отражает усиление учебной подготовки наиболее одарённых людей); (b) m_T = 0,7 и σ_T = 0,1 (что изображает повышение среднего уровня образованности). Также показаны соответствующие значения m_T и m_T ± σ_T, в виде вертикальных прерывистой и точечных линий, соответственно.

Фактически, это приводит к тому, что повышение σ_T, при неизменном значении m_T, как показано на схеме (a), поднимает шансы наиболее талантливых людей на достижение очень высокой успешности – лучший исполнитель теперь является очень одарённым агентом, с T = 0,97, достигшим невероятного уровня капитала / успешности C_best = 655360. Это, с одной стороны, может быть оценено положительно, однако, с другой стороны, является единичным случаем и также наблюдается, в качестве противовеса, рост разрыва между неудачливыми и везучими людьми. Взглянув теперь на схему (b) видим, что повышение m_T без изменения σ_T даёт лучшего исполнителя с C_best = 327680 и талантом T = 0,8, следом за которым идут ещё двое, с C = 163840 и, соответственно, T = 0,85 и T = 0,92. Это говорит о том, что и в данном случае повысились шансы наиболее талантливых людей достичь крайне высокого успеха, но в это же время разрыв между неудачливыми и везучими людьми оказался ниже прежнего.

Наконец, в обоих рассмотренных примерах среднее значение капитала / успешности наиболее талантливых из 100 прогонок людей возросло по отношению со значением C_mt ≈ 63, полученным в подразделе 2.2. В частности, мы получили C_mt ≈ 319 на схеме (a) и C_mt ≈ 122 на схеме (b), но данные результаты весьма специфичны для конкретной серии прогонок симуляции. Более надёжный параметр численного выражения эффективности исследуемых здесь социальных политик, – им снова является показатель P_T, представленный в предыдущем подразделе, т.е. средняя доля индивидов с талантом T > m_T + σ_T и итоговыми успешностью / капиталом C_end > 10, относительно общего числа людей с талантом T > m_T + σ_T (обратите внимание, что здесь, в обоих рассматриваемых случаях, m_T + σ_T = 0,8). Так, мы получили P_T = 38% в схеме (a) и P_T = 37,5% для схемы (b), с незначительным чистым приростом по отношению к эталонному значению P_T0 = 32% (полученному для распределения таланта при m_T = 0,6 и σ_T = 0,1).

Подводя черту, наши результаты показывают, что усиление учебной подготовки наиболее одарённых людей или повышение среднего уровня образованности приводит, как того можно было ожидать, к некоторым положительным эффектам в социальной системе, так как обе этих политики ведут к росту вероятности талантливых индивидов на реализацию возможностей, предоставляемых им удачей. С другой стороны, улучшения в средней доле высокоталантливых людей, сумевших достичь хорошего уровня успеха, похоже, являются не особо значимыми для обоих проанализированных сценариев. Таким образом, результат соответствующих образовательных политик, похоже, в основном ограничивается возникновением изолированных случаев исключительной успешности.

Конечно, как только данный уровень образованности был установлен, стало очевидно, что обилие возможностей, предлагаемых той социальной средой, т.е. страной, где кто-либо по случайности родился или решил проживать, является ещё одной ключевой составляющей, способной влиять на глобальные показатели системы.

На рисунке 14 мы привели результаты, сходные с теми, что были видны на предыдущем изображении, но для другой серии симуляций, со 100 прогонками каждая, при таких же установленных параметрах, что и в подразделе 2.2 (N = 1000, m_T = 0,6, σ_T = 0,1, I = 80, C(0) = 10, N_E = 500) но с разными процентами p_L удачных событий (напомним, что в подразделе 2.2 был взят процент p_L = 50%). На схеме (a) мы принимаем p_L = 80%, чтобы симулировать высоко стимулирующую среду, изобилующую возможностями, типичную для богатых индустриализированных стран вроде США [26]. С другой стороны, на схеме (b) значение p_L = 20% воспроизводит сценарий намного менее поощряющего окружения, с крайне малым количеством возможностей, такого как, например, в странах «третьего мира».

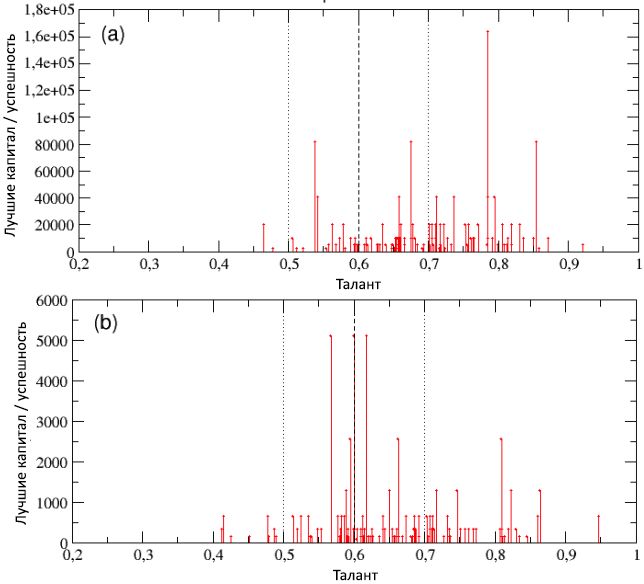
Рисунок 14: итоговый капитал наиболее успешных индивидов в каждой из 100 прогонок показан в виде функции от их таланта для популяций, живущих в средах с разным процентом p_L удачных событий: (a) p_L = 80%; (b) p_L = 20%. Также вертикальными прерывистой и точечными линиями отмечены, соответственно, значения m_T = 0,6 и m_T ± σ_T, при σ_T = 0,1.

Как видно из обеих схем, итоговые успешность / капитал наиболее удачливых индивидов, представленные в виде функции от их таланта, находятся в сильной зависимости от p_L.

При p_L = 80%, как на схеме (a), несколько агентов со средне-высоким талантом смогли достичь более высоких, по сравнению со сценарием p_L = 50%, уровней успеха, с пиковым C_best = 163840. С другой стороны, среднее значение капитала / успешности самых талантливых индивидов, C_mt ≈ 149, находится довольно высоком уровне и, что ещё важней, то же относится и к показателю P_T = 62,18% (который примерно вдвое больше эталонного значения P_T0 = 32%), это значит, что, как и ожидалось, наиболее талантливые люди выигрывают от большего процента удачных событий.

Совершенно иные результаты получены при p_L = 20%. Безусловно, как видно из схемы (b), общий уровень успешности теперь очень низкий, по сравнению с тем, что был найден в симуляциях из подраздела 2.2, с пиковым значением C_best составляющим лишь 5120 единиц – это след понижения социальных неравенств, который является ожидаемым последствием выравнивания возможностей в достижении успеха. В соответствии с данными результатами, показатель P_T также достигает минимального значения, со средним процентом талантливых индивидов, сумевших нарастить свой первоначальный уровень успешности, равным всего 8.75%.

По итогу, в данном разделе было показано, что поощряющая среда и изобилие возможностей, связанное с соответствующей стратегией распределения финансов и ресурсов, являются важными факторами в реализации потенциала наиболее талантливых людей, давая им больше шансов на достижение успеха по сравнению с умеренно одарёнными, но более удачливыми. С точки зрения макроуровня, любая политика, способная повлиять на данные показатели и поддержать талантливых индивидов, в результате обеспечит коллективный прогресс и инновационность.

4. Финальные замечания

В данной работе, начав с ряда крайне простых и рациональных предположений, мы представили агентную модель, которая смогла количественно измерить роль таланта и удачи в успешности карьер людей. Симуляции показали, что, хотя талант имеет среди агентов Гауссово распределение, итоговое распространение успешности / капитала, спустя 40 лет рабочей жизни, следует степенной функции по принципу закона Парето «80/20», что соответствует характеру распределению богатств, наблюдаемому в реальном мире. Важный результат симуляций заключается в том, что наиболее успешные агенты практически всегда являются не самыми талантливыми, а теми, кто близок к среднему значению Гауссового распределения таланта – широкоизвестный факт, часто встречаемый в литературе. Модель показывает часто недооцениваемую важность удачных событий в определении итогового уровня успешности индивида. Так как вознаграждения и ресурсы обычно раздаются тем, кто уже достиг высокого уровня успешности, ошибочно используемого в качестве меры компетенции / таланта, то это приводит к отрицательному стимулированию, вызывающего недостаток возможностей для наивысших талантов. Наши результаты подчёркивают риски парадигмы, которую мы называем «недалёкая меритократия», не способной уважать и награждать самых компетентных людей, так как она недооценивает роль случайности в числе главных определяющих факторов успеха. В связи с этим было изучено несколько различных сценариев с целью выявления наиболее эффективных стратегий, способных уравновесить непредсказуемую роль удачи и дать больше возможностей и ресурсов самым талантливым – намерение, которое должно являться главной целью истинно меритократичного подхода. Было также показано, что эти стратегии являются наиболее выгодными для сообщества в целом, так как они ведут к росту различных идей и перспектив в исследованиях, тем самым также стимулируя инновационность.

Благодарности

Мы хотим поблагодарить Роберта Франка, Павла Собковица и Константино Тсаллиса за плодотворные дискуссии и комментарии.

Библиография

Bak, P., Tang, C. and Wiesenfeld, K., Self-organized criticality. Phys. Rev. A, 38:364{374 (1988).
Barab´asi, A.-L., Albert, R., Emergence of Scaling in Random Networks, Science, Vol. 286, Issue 5439, pp. 509{512 (1999).
Newman, M. E. J., Power laws, Pareto distributions and Zipf’s law, Contemporary Physics, 46 (5): 323{351 (2005).
Tsallis, C., Introduction to Nonextensive Statistical Mechanics. Approaching a Complex World, Springer (2009).
Pareto, V., Cours d’Economique Politique, vol. 2 (1897).
Steindl, J., Random Processes and the Growth of Firms — A Study of the Pareto Law, Charles Griffin and Company, London (1965).
Atkinson, A. B., Harrison, A. J., Distribution of Total Wealth in Britain, Cambridge University Press, Cambridge (1978).
Persky, J., Retrospectives: Pareto’s law, Journal of Economic Perspectives 6, 181{192 (1992).
Klass, O. S., Biham, O., Levy, M., Malcai, O., Solomon, S., The Forbes 400 and the Pareto wealth distribution, Economics Letters 90, 290{295 (2006).
Hardoon, D., An economy for the 99%, Oxfam GB, Oxfam House, John Smith Drive, Cowley, Oxford, OX4 2JY, UK (January 2017).
Bouchaud, J.-P., M´ezard, M., Wealth condensation in a simple model of economy, Physica A 282, 536{54 (2000).
Dragulescu, A. and Yakovenko, V. M., Statistical mechanics of money, Eur. Phys. J. B 17, 723{729 (2000).
Chakraborti, A. and Chakrabarti, B. K., Statistical mechanics of money: how saving propensity affects its distribution, Eur. Phys. J. B 17, 167{170 (2000).
Patriarca, M., Chakraborti, A., Germano, G., Influence of saving propensity on the power law tail of wealth distribution, Physica A 369(2), 723{736 (2006).
Scalas, E., Random exchange models and the distribution of wealth. European Physical Journal — Special Topics, 225. pp. 3293-3298. ISSN 1951{6355 (2016).
During, B., Georgiou, N. and Scalas, E., A stylised model for wealth distribution. In Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science. Springer Singapore, Singapore, pp. 95{117. ISBN 9789811057045 (2017).
During, Bertram, Georgiou, Nicos and Scalas, Enrico (2017) A stylised model for wealth distribution. In: Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science. Springer Singapore, Singapore, pp. 95-117. ISBN 9789811057045
Sinatra, R., Wang, D., Deville, P., Song, C. and Barab´asi, A.-L., Quantifying the evolution of individual scientific impact, Science 354, 6312 (2016).
Einav, L. and Yariv, L., What’s in a Surname? The Effects of Surname Initials on Academic Success, Journal of Economic Perspective, Vol. 20, n. 1, p.175{188 (2006).
Ruocco, G., Daraio, C., Folli, V. and Leonetti, M., Bibliometric indicators: the origin of their log-normal distribution and why they are not a reliable proxy for an individual scholar’s talent, Palgrave Communications 3:17064 doi: 10.1057/palcomms.2017.64 (2017).
Jurajda, S., Munich, D., Admission to Selective Schools, Alphabetically, Economics of Education Review, Vol. 29, n. 6, p.1100{1109 (2010).
Van Tilburg, W. A. P., Igou, E. R., The impact of middle names: Middle name initials enhance evaluations of intellectual performance, European Journal of Social Psychology, Vol. 44, Issue 4, p.400{411 (2014).
Laham, S. M., Koval, P., Alter, A. L., The name-pronunciation effect: Why people like Mr. Smith more than Mr. Colquhoun, Journal of Experimental Social Psychology 48, p.752{756 (2012).
Silberzahn, R., Uhlmann, E. L., It Pays to be Herr Kaiser: Germans with Noble-Sounding Last Names More Often Work as Managers, Psychological Science 24(12): 2437{44 (2013).
Coffey, B. and McLaughlin, P., From Lawyer to Judge: Advancement, Sex, and NameCalling. SSRN Electronic Journal, DOI10.2139/ssrn.1348280 (2009).
Milanovic, B., Global Inequality of Opportunity: How Much of Our Income Is Determined by Where We Live?, Review of Economics and Statistics, 97.2 (2015): 452{60.
Du, Q., Gao, H., Levi, M. D., The relative-age effect and career success: Evidence from corporate CEOs, Economics Letters 117(3):660{662 (2012).
Deaner, R. O., Lowen, A., Cobley, S., Born at the Wrong Time: Selection Bias in the NHL Draft. PLoS ONE 8(2): e57753 (2013).
Brooks, D., The Social Animal. The Hidden Sources of Love, Character, and Achievement, Random House, 424 pp. (2011).
Iacopini, I., Milojevic, S. and Latora, V., Network Dynamics of Innovation Processes, Physical Review Letters 120, 048301 (2018).
Tomasetti, C., Li, L., Vogelstein, B., Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention, Science 355, 1330{1334 (2017).
Newgreen, D. F. et al., Differential Clonal Expansion in an Invading Cell Population: Clonal Advantage or Dumb Luck?, Cells Tissues Organs 203:105{113 (2017).
Snyder, R. E. and Ellner, S. P., We Happy Few: Using Structured Population Models to Identify the Decisive Events in the Lives of Exceptional Individuals, The American Naturalist 188, no. 2 (2016): E28{E45.
Snyder, R. E. and Ellner, S. P., Pluck or Luck: Does Trait Variation or Chance Drive Variation in Lifetime Reproductive Success?, The American Naturalist 191, no. 4 (2018): E90{E107.
Талеб Н.Н., Одураченные случайностью. О скрытой роли шанса в бизнесе и в жизни, Манн, Иванов и Фербер (2018).
Талеб Н.Н., Черный лебедь. Под знаком непредсказуемости, КоЛибри (2018).
Mauboussin, M. J., The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, Harvard Business Review Press (2012).
Фрэнк Р.Х., Успех и удача. Фактор везения и миф меритократии, Высшая Школа Экономики (2019).
Watts, D. J., Everything Is Obvious: Once You Know the Answer, Crown Business (2011).
Salganik, M. J., Dodds P. S., Watts D. J., Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market, Science Vol.311 (2006)
Travis, M., Hofman, J. M., Sharma, A., Anderson,. A., Watts, D. J., Exploring limits to prediction in complex social systems, Proceedings of the 25th ACM International World Wide Web Conference (2016) arXiv:1602.01013 [cs.SI]
Stewart, J., The Distribution of Talent, Marilyn Zurmuehlin Working Papers in Art Education 2: 21-22 (1983).
Sinha, S. and Pan, R. K., How a «Hit» is Born: The Emergence of Popularity from the Dynamics of Collective Choice, In Econophysics and Sociophysics: Trends and Perspectives (eds B. K. Chakrabarti, A. Chakraborti and A. Chatterjee), Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany. doi: 10.1002/9783527610006.ch15 (2006).
Fortin, J.-M., Curr, D. J., Big Science vs. Little Science: How Scientific Impact Scales with Funding, PLoS ONE 8(6): e65263 (2013).
Jacob, B. A., Lefgren, L., The impact of research grant funding on scientific productivity, Journal of Public Economics 95 (2011) 1168{1177.
O’Boyle, JR. E. and Aguinis, H., The Best and the Rest: revisiting the norm of normality of individual performance, Personnel Psychology, 65: 79-119. doi:10.1111/j.1744-6570.2011.01239.x (2012).
Denrell, J. and Liu, C., Top performers are not the most impressive when extreme performance indicates unreliability, Proceedings of the National Academy of Sciences, 109(24):9331{9336 (2012).
Pluchino, A., Rapisarda, A., and Garofalo, C., The Peter principle revisited: A computational study, Physica A 389(3):467{472 (2010).
Pluchino, A., Garofalo, C., Rapisarda, A., Spagano, S. and Caserta, M., Accidental politicians: How randomly selected legislators can improve parliament efficiency, Physica A 390(21):3944{3954 (2011).
Pluchino, A., Rapisarda, A. and Garofalo, C., Efficient promotion strategies in hierarchical organizations, Physica A 390(20):3496{3511 (2011).
Biondo, A. E., Pluchino, A., Rapisarda, A., Helbing, D., Reducing financial avalanches by random investments, Phys. Rev. E 88(6):062814 (2013).
Biondo, A. E., Pluchino, A., Rapisarda, A., Helbing, D., Are random trading strategies more successful than technical ones, PLoS One 8(7):e68344 (2013)
Biondo, A. E., Pluchino, A., Rapisarda, A., The beneficial role of random strategies in social and financial systems, J. Stat. Phys. 151(3-4):607{622 (2013).
Biondo, A. E., Pluchino, A., Rapisarda, A., Micro and macro benefits of random investments in financial markets, Cont. Phys. 55(4):318{334 (2014).
Biondo, A. E., Pluchino, A., Rapisarda, A., Modeling financial markets by self-organized criticality, Phys. Rev. E 92(4):042814 (2015).
Wilensky, U., NetLogo. ccl.northwestern.edu/netlogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999).
Merton, R. K., The Matthew effect in science, Science 159, 56-63 (1968).
Мертон Р. К., Эффект Матфея в науке, II: Накопление преимуществ и символизм интеллектуальной собственности, https://www.hse.ru/data/033/314/1234/3_6_1Merto.pdf.
Bol, T., de Vaan, M. and van de Rijt, A., The Matthew effect in science funding, Proceedings of the National Academy of Sciences, DOI: 10.1073/pnas.1719557115 (2018).
Mongeon, P., Brodeur, C., Beaudry, C. et al., Concentration of research funding leads to decreasing marginal returns, Research Evaluation 25, 396{404 (2016).
Merton, R. K., Barber, E., The Travels and Adventures of Serendipity, Princeton University Press, Princeton (2004).
Murayama, K. et al., Management of science, serendipity, and research performance, Research Policy 44 (4), 862{873 (2015).
Benias, P. C. et al., Structure and Distribution of an Unrecognized Interstitium in Human Tissues, Scientific Reports, vol. 8, 4947 (2018).
Flexner, A, The Usefulness of Useless Knowledge, Princeton University Press, Princeton (2017).
Lucky science. Scientists often herald the role of serendipity in research. A project in Britain aims to test the popular idea with evidence., Nature Editorial, Vol.554, 1 February 2018.
Yaqub, O., Serendipity: Towards a taxonomy and a theory, Research Policy 47, 169{179 (2018).
Page, S. E., The Diversity Bonus. How Great Teams Pay Off in the Knowledge Economy, Princeton University Press (2017).
Cimini, G., Gabrielli, A., Sylos Labini, F., The Scientific Competitiveness of Nations, PLoS ONE 9(12): e113470. doi.org/10.1371/journal.pone.0113470 (2014).
Curry, S., Let’s move beyond the rhetoric: it’s time to change how we judge research, Nature 554, 147 (2018).
Nicholson, J. M. and Ioannidis, J. P. A., Research grants: Conform and be funded, Nature 492, 34{36 (2012).
Bollen, J., Crandall, D., Junk, D. et al., An efficient system to fund science: from proposal review to peer-to-peer distributions, Scientometrics 110, 521{528 (2017).
Garner, H. R., McIver, L. J. and Waitzkin, M. B., Research funding: Same work, twice the money?, Nature 493,599{601 (2013).