Математики доказали, что случайный процесс в применении к случайной поверхности неизменно порождает определённые закономерности

В оригинале статьи это трёхмерное изображение, которое можно покрутить
В фильме про поиски потерянного Ковчега Индиане Джонсу пришлось искать потайную комнату, скрывавшую легендарный Ковчег Завета. Для определения его точного местоположения Индиане нужно было найти особую карту, видимую только тогда, когда солнце светит через особый кристалл в определённой комнате в определённое время дня.
Подобная идея – что важнейшую информацию можно раскрыть только при точном совпадении определённых обстоятельств – встречается во многих мифах. Встречается она и в математике, иногда в неожиданных ситуациях. Вот теперь три математика доказали, что если очень точно настроить определённый тип случайности, то на свет появляются замысловатые геометрические фигуры – будто карта с кладом на обычном полу.
Эти фигуры похожи на шахматные клетки, разбросанные по решёткам, которые в свою очередь сами созданы случайным процессом. Можно было бы подумать, что нагромождая случайность на случайность, мы получим неразбериху. Оказывается, что как и в случае со снежинками, когда каждая из них уникальна, но при этом все они – снежинки, так и беспорядок сходится к универсальной форме – если только условия окажутся точно такими, как нужно.
Поворотный момент
Все знают, что математики изучают формы. Большая часть из этих форм следует детерминистским правилам: если я дам вам инструкции по построению сферы, вы каждый раз будете получать одну и ту же сферу.
Но ещё математики изучают формы, получаемые в результате случайных процессов, такого, например, как случайное блуждание – путь, направление каждого шага которого выбирается случайным образом. Кроме случайного блуждания существуют и другие виды случайных геометрических объектов, например, случайные двумерные поверхности (представьте себе ландшафт, где холмы и впадины разбросаны случайным образом) и случайные карты (набор из случайных точек, соединённых линиями).
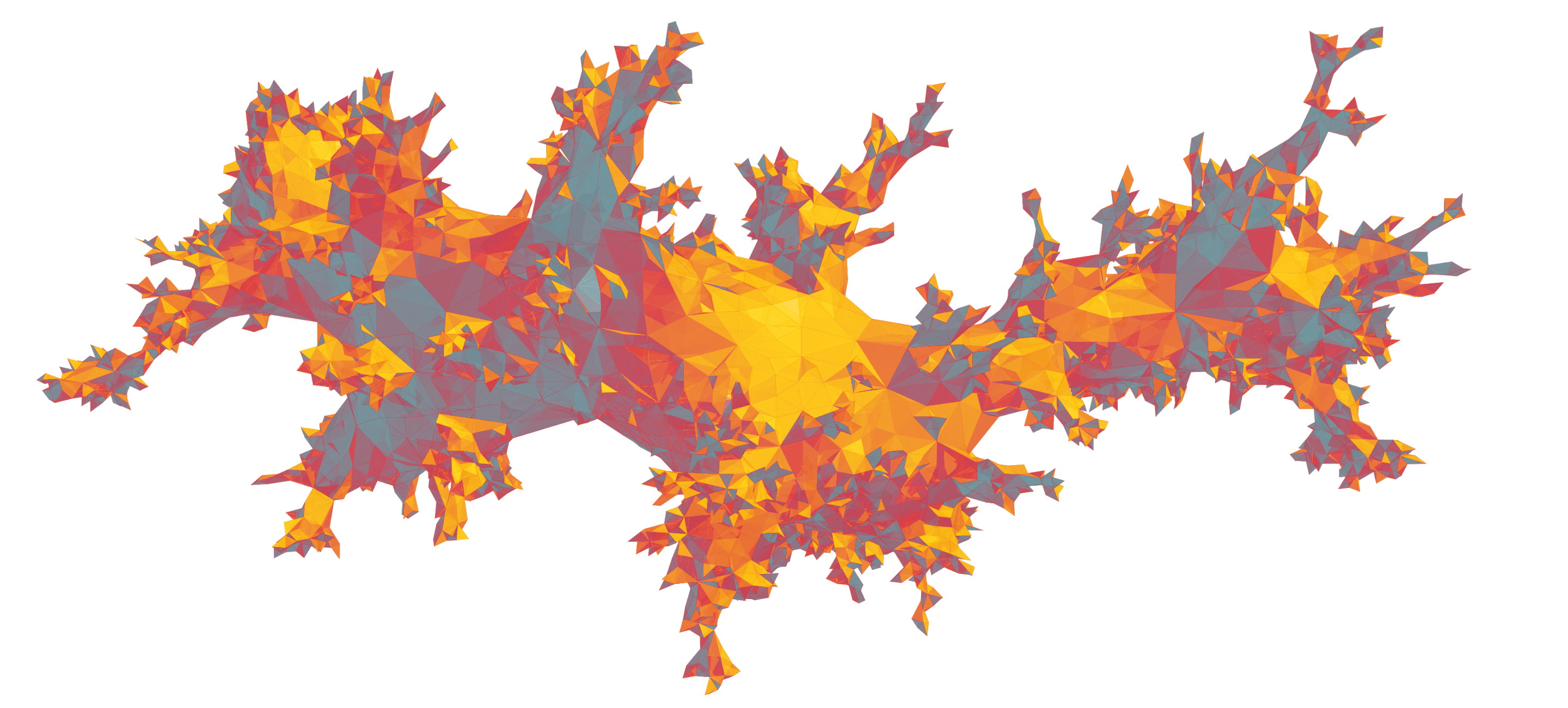
Случайная поверхность, полученная склейкой треугольников
Все такие формы отличаются друг от друга. Однако математики обнаружили, что эти случайные процессы сходятся к определённым каноническим формам. К примеру, все случайные блуждания являются формой броуновского движения при достаточно долгом блуждании. В последние годы математики открыли канонические формы и других случайных процессов – и получили за это высшие награды в своих областях.
Новое доказательство связано с пониманием глубинных свойств ещё одного случайного процесса.
Он начинается с создания случайной поверхности. Сначала нужно склеить треугольники сторонами. Затем их нужно сопоставить вместе любым образом, только чтобы полученная форма была замкнутой, как упаковка на подарке (не имела отверстий). Если вы начнёте с определённым количеством треугольников на руках, у вас будет множество возможностей. Некоторые из таких «триангуляций» породят почти гладкие поверхности, похожие на шар. Большинство из них будет выглядеть более шероховато – как экстремальные поверхности, напоминающие горные хребты.
«Она не будет похожей на обычную сферу, у неё будут такие большие шипы», — сказал Оливье Бернарди, математик из Брандейского университета, соавтор работы, в которой также участвовали Николас Курьен из университета Париж-юг XI и Грегори Мьермонт из высшей нормальной школы в Лионе.

Оливье Бернарди, Николас Курьен и Грегори Мьермонт
Мьермонт и другой математик, Жан-Франсуа ле Галл, установили многие свойства этих случайных триангуляций в своей предыдущей работе. Новое доказательство идёт ещё дальше, добавляя второй слой случайности поверх случайной триангуляции.
Чтобы добавить новую случайность, отметьте каждую точку, в которой треугольники встречаются углами – то, что математики называют вершиной. Раскрасьте вершины случайным образом в чёрный или белый цвет. Можно делать это, подбрасывая монетку, хотя монетка может быть не совсем честной, и перевешивать на одну сторону.
Раскрасив вершины, можно задавать различные вопросы по поводу созданной вами закономерности. Один из базовых: насколько далеко можно пройти по поверхности, используя только одни чёрные вершины? Процесс движения по связанным вершинам одного цвета называется просачиванием. Это математический способ изучать физическое явление с тем же названием, когда жидкость проходит сквозь пористую среду.
Просочиться будет легко (или не очень), в зависимости от того, как распределён вес монеты: если монета склоняется к выдаче чёрных вершин, просачивание почти гарантировано; если к выдаче белых, просачивание почти наверняка будет невозможным.
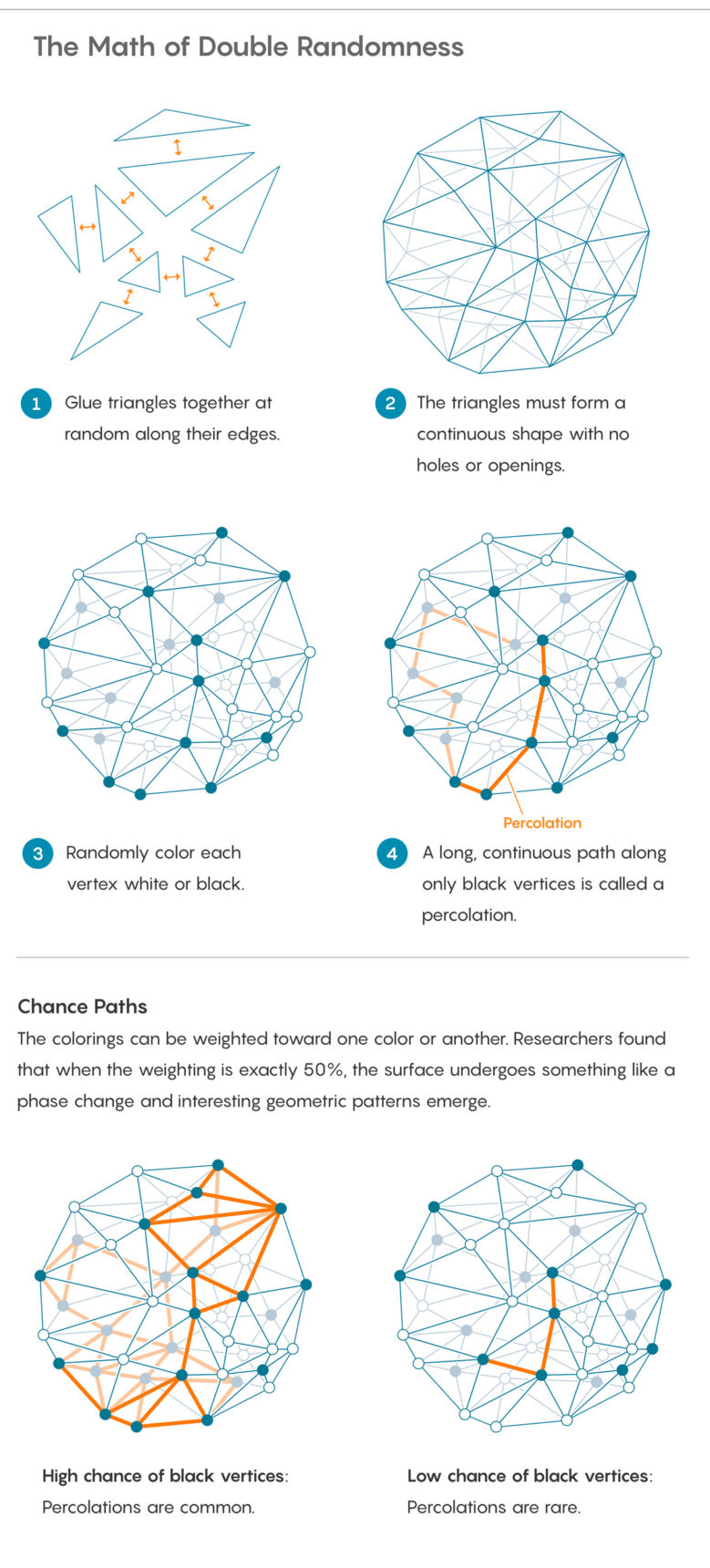
Бернарди, Курьен и Мьермонт изучают случаи, попадающие в промежуток между этими экстремумами – поворотный момент в изменении веса монеты, когда просачивание превращается из почти невозможного в почти гарантированное явление. Они называют эту точку «критическим порогом». Это пример фазового перехода, того волшебного момента, когда горячая вода внезапно становится паром.
«Критический порог означает, что если я слегка передвину мои параметры, то поведение моей системы изменится от драматического к драматическому с другим знаком», — сказал Курьен.
Физикам интересны фазовые переходы потому, что многие из важнейших природных явлений случаются как раз на грани. Математикам тоже интересны фазовые переходы, поскольку важные математические свойства часто появляются как раз в этих точках.
«Мы знаем, что вода кипит при 100 градусах, создавая все эти сумасшедшие закономерности, и образуется пар», — сказал Скотт Шеффилд, математик из MIT. «Иногда такое безумное и дикое поведение становится очень интересным. Этот фазовый переход призывает нас разобраться в нём».
В новой работе три математика доказывают, что подобное безумное поведение проявляется как раз в фазовом переходе просачивания. Они показывают, что на этом критическом пороге появляется геометрическая форма – уникальная, и в то же время универсальная.
Скрытый порядок в случайности
В первой части работы определяется, как именно подправить монетку так, чтобы раскраска вершин попала на порог между наличием и отсутствием просачивания. Подтверждая интуицию, они доказывают, что критическим значением служит идеальная монета – дающая 50% шанс на выпадение чёрного цвета, и 50% на выпадение белого.
«Это первая часть работы. Мы доказываем, что ровно на половине происходит нечто интересное», — сказал Бернарди.
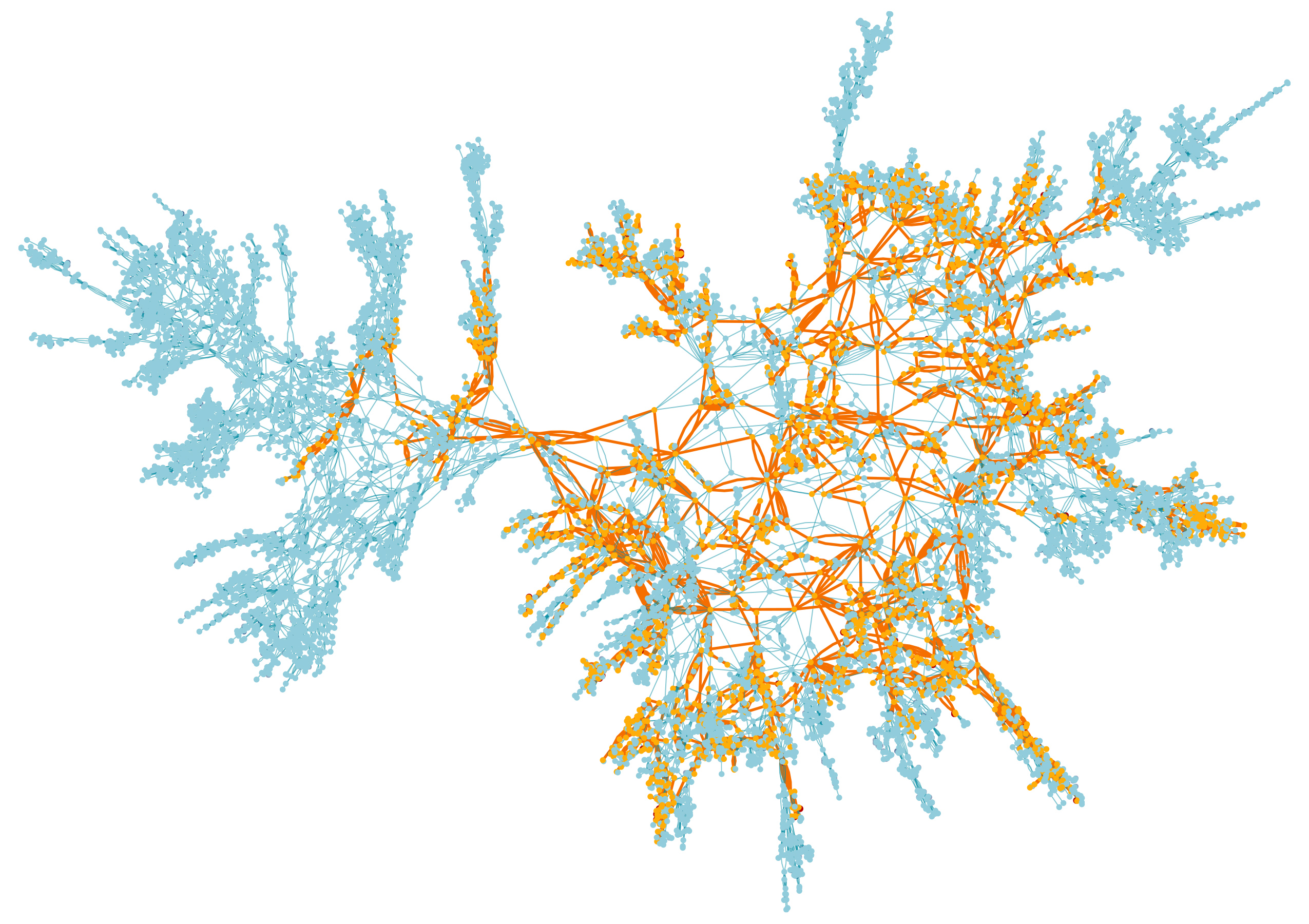
Карта вершин случайной поверхности, крупнейшее скопление отмечено оранжевым
Во второй части изучается то самое нечто, что там происходит. Раскрашивая вершины в чёрные и белые цвета при помощи честной монеты, вы получаете хороший баланс между скоплениями чёрных и белых вершин. Скопления растут вокруг друг друга, как заросли сорняков, соперничающие за место в разросшемся саду, создавая сложные геометрические фигуры, которых не появляется, в случае, когда среди вершин доминирует один из цветов.
«Выбирая критический параметр, вы обнаруживаете появление больших скоплений, — сказал Шеффилд. – Однако они не окрашивают всё целиком, и не бывают мелкими».
Поскольку поверхность создана случайным образом, и процесс раскраски вершин также случаен, то крупное скопление на одной поверхности всегда будет отличаться от крупного скопления на другой. Но математики доказали, что для всех поверхностей и всех возможных способов раскрасить их вершины, у крупнейших скоплений будут одни и те же свойства. Первое, что они доказали – точное распределение вероятности размеров крупнейших чёрных скоплений по всем поверхностям. Они установили, что чаще всего встречается скопление определённого промежуточного размера, и что частота, с которой появляются более крупные или мелкие скопления, увеличивается экспоненциально при удалении от этого промежуточного.
Они также доказывают, что все крупные кластеры можно привести к одной каноничной форме, известной, как «стабильная карта». Стабильная карта относится к этим скоплениям так же, как броуновское движение к случайному блужданию. Это значит, что если немного отдалить отдельные скопления – так, чтобы каждый случайный шаг внутри скопления был менее заметным в геометрии всей фигуры в целом – то скопления постепенно придут к общей форме. Они похожи на снежинки: вблизи кажутся уникальными, но издалека явно видна их общность.
«Они нашли эту стабильную карту, естественный предел масштабирования», — сказал Шеффилд.
Работа расширяет пределы знаний, касающихся случайных форм и процессов, накопленных математиками в последние годы. Она также открывает нам, что именно в тот момент, когда случайная система кажется наиболее хаотичной, сквозь неё начинает проглядывать исключительный геометрический порядок.
Источник

