Intro

Этот пост написан под впечатлением от вот этого отличного поста с Хабра, в котором автор наглядно, при помощи двумерных моделек, которые рисует его программа, объясняет как работает Специальная Теория Относительности.

Я работаю в IT, а по образованию – физик-теоретик. Уже долгое время увлекаюсь популяризацией науки, и теоретической физики в частности. Постараюсь аналогично вышеупомянутому посту о специальной теории относительности объяснить на специально подготовленном примере как работает квантовая механика.

Модель, которую я рассматриваю – отнюдь не нова. Более полугода назад Chris Cantwell разместил на YouTube анонс новой настольной игры: квантовых шахмат (многим, возможно, известно об этом из вот этого вирусного ролика).

Недавно игра вышла в Steam, она стоит 249 руб. Есть ещё другая реализация – бесплатное приложение для iOS (не знаю, есть ли оно в Google Play). Однако в процессе игр с друзьями я экспериментально выяснил, что она неправильная с точки зрения квантовой механики. Такую реализацию скорее можно назвать статистическими шахматами, а не квантовыми.

Поэтому я решил написать свою реализацию, с запутанностью и суперпозициями. В своей реализации я постарался исправить те недостатки, которые на мой взгляд присутствуют в версии на Steam (например, у меня пешки тоже могут ходить квантовыми ходами, как и все остальные фигуры). Про приложение для iOS и так всё понятно: любая реализация квантовых шахмат должна быть по-настоящему квантовой, т.е. не только быть вероятностной, но поддерживать такие эффекты квантовой механики как интерференция, запутанность, etc.

Альфа-версия хостится по адресу http://solenodonus.com/truly-quantum-chess. Там можно поиграться самому с собой, «играя» за двух игроков по очереди; либо сыграть с другом полноценную партию. Игровой процесс проходит прямо в браузере, не нужно ничего скачивать и устанавливать.

Дисклеймер: я не претендую на полное описание законов квантовой физики. Но зато в посте не будет ни одной формулы: только картинки, только хардкор.

Суперпозиции

Так всё-таки, чем же эти шахматы квантовые? Основное их отличие от обычных шахмат состоит в том, что игра ведётся на суперпозиции шахматных досок. Выражаясь простым языком – на нескольких досках одновременно.

Это выглядит примерно вот так:

Синяя пешка находится в суперпозиции: она занимает позиции e2 и e4 одновременно.
То же самое верно для красного коня: он находится в суперпозиции позиций g8 и e3.

Что же это означает, на самом деле?

Читателя, который ждёт разъяснений по поводу того, что же на самом деле означает суперпозиция, я вынужден разочаровать: разъяснений по просту не существует.

Суперпозиции – это просто суперпозиции. Они действительно существуют в природе. Мы почти не наблюдаем их в повседневной жизни из-за декогеренции – взаимодействия с хаотической окружающей средой, в результате которого суперпозиции быстро разрушаются.

Однако, ничто принципиально не мешает нам обеспечить условия, в которых суперпозиция сохранится на длительное время. Именно такая задача стоит, например, перед инженерами, работающими над созданием квантового компьютера.

Вероятности

Существует и другая интерпретация суперпозиций. Можно сказать, что синяя пешка находится не на двух клетках c2 и c4 одновременно, а на какой-то одной из этих клеток. Просто мы не знаем, на какой. Более того, вероятность нахождения на каждой из клеток равна 50% (что показано при помощи горизонтальной полоски, делящей каждую половинку пешки пополам).

Оказывается, что в реальности

• Первая интерпретация (пешка на e2 и e4 одновременно) – более точна, когда система не взаимодействует с измерительным прибором. Про то, что считать измерительным прибором на шахматной доске, речь пойдёт далее в разделе про коллапс.
• Вторая интерпретация (пешка либо на e2, либо на e4, мы просто не знаем где) – более точна в момент взаимодействия с окружением, например с измерительным прибором.

Пока взаимодействия нет, оба варианта (пешка на e2 и на e4) существуют сами по себе. Игра ведётся на суперпозиции вариантов. Это – сложный процесс, который, естественно, перемешивает оба варианта, заставляя их влиять друг на друга. Поэтому нельзя сказать, что существует только один вариант.

Когда включается взаимодействие, верна вероятностная интерпретация. Вероятност нахождения пешки на e2 в данном случае равна 50%. Движок квантовых шахмат по необходимости разрешает такие ситуации, выбирая вариант при помощи генератора случайных чисел.

Как мне создать суперпозицию?

В обычные шахматные правила добавляется одно важное изменение: за каждый ход игрок может совершить либо обычный шахматный ход, либо т.н. квантовый ход.

• Обычный ход – просто ход шахматной фигурой, по правилам обычных шахмат. Если игра на данный момент ведётся на суперпозиции, то ход совершается на всех досках суперпозиции, где он разрешён по правилам шахмат. Это, кстати, далеко не так тривиально, как кажется. Например, если на пути ладьи оказывается пешка, находящаяся в суперпозиции, то такой ход возможен только если пешки нет (т.к. ладья по правилам не может перепрыгивать через фигуры). Поэтому после такого обычного хода ладья сама окажется в суперпозиции: на доске, на которой пешки нет, она совершила ход; а на доске, на которой на пути находится пешка, ход запрещён, поэтому ладья остаётся на месте.

• Квантовый ход – ход, при помощи которого можно ввести шахматную доску в суперпозицию. Квантовый ход состоит из двух обычных ходов подряд одной и той же фигурой. Оба хода должны быть правильными с точки зрения обычных шахмат (правильнее сказать, ход применяется на доске из суперпозиции, если оба хода правильны с точки зрения обычных шахмат на этой доске). Своеобразной «платой» за возможность сходить дважды подряд является то, что после квантового хода фигура переходит в суперпозицию: она одновременно и делает два хода, и остаётся на месте. Впоследствии, когда произойдёт взаимодействие (см. далее про «коллапс»), при помощи генератора случайных чисел решится, какая из двух частей суперпозиции существует, а какая нет. Но пока обе части существуют одновременно.

Чтобы сделать обычный ход, нужно кликнуть по фигуре (выделится зелёным), а затем по клетке, на которую хочется сходить. Чтобы сделать квантовый ход, нужно два раза кликнуть по фигуре (выделится фиолетовым), затем один раз кликнуть по промежуточной клетке (выделится зелёным), а затем по финальной.

Также правилами разрешено делать единичные квантовые ходы, т.е. квантовые ходы, при которых фигура делает не два хода подряд, а один.

Важное ограничение: по правилам нельзя есть вражескую фигуру при квантовом ходе. Такая возможность делает игру слишком непредсказуемой. Квантовый ход можно делать только на пустую клетку.

Dead and alive

Частный случай суперпозиции, представляющий особый интерес – это суперпозиция, при которой фигура одновременно жива и мертва. Возьмём для примера квантовую шахматную доску из примера выше. После хода синей пешкой f2:e3 красные теряют половину своего коня…

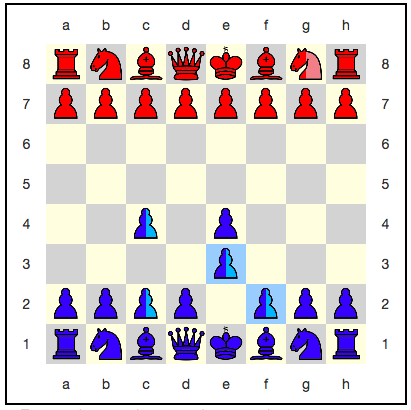
Во-первых, синяя пешка сама оказалась в суперпозиции. Это происходит потому, что пешки по-разному ходят и едят. На доске, на которой красный конь был на e3, пешка его успешно съела и перешла на e3. На доске, на которой коня там небыло, пешка не могла сделать такой ход, т.к. ей было нечего есть. Поэтому она осталась на f2.

Красный конь оказался одновременно и живым, и мёртвым. Когда-нибудь в будущем, когда произойдёт взаимодействие с измерительным прибором (подробнее про это см. ниже в разделе «коллапс»), при помощи генератора случайных чисел разрешится эта ситуация. Либо окажется, что у красных есть конь, либо окажется что его нет. Вероятность исходов – 50%.

Примечательно, что пока ситуация не разрешилась и конь находится в суперпозиции, красные могут продолжать играть половиной своего коня. Правда, с вероятностью 50% окажется что каждый ход этой половиной коня – это просто потеря хода.

Шах и мат

Шахи и маты реальзовать крайне сложно, потому что не понятно как быть в ситуации когда король находится в суперпозиции шаха и не шаха; мата и не мата. Поэтому правила обычных шахмат были упрощены: шахов и матов нет; для того, чтобы выиграть в квантовые шахматы нужно съесть вражеского короля.

Примечательно, что король, как и любая другая фигура, может находиться в суперпозиции. Если съесть половину короля, то выигрыш обеспечен с вероятностью 50%. Однако, игра в этом случае продолжается! Если, скажем, после этого вашего короля съели – то это не значит, что вы проиграли. Ведь вашего короля съели только на тех досках суперпозиции, где вы ещё не выиграли! Т.е. будет сгенерировано случайное число, и вы проиграете/выиграете с вероятностью 50%.

Это один из примеров проявления того самого «взаимодействия с измерительным прибором», которое разрушает суперпозиции на квантовой шахматной доске.

Кнопка Capitulate тоже далеко не так проста, как кажется. Капитуляция проходит только на тех досках из суперпозиции, на которых игра ещё идёт. Т.е. если вы находитесь в суперпозиции, в которой уже выиграли с вероятностью 75% (т.е. у врага 25% короля) и вы нажимаете Capitulate, то вы проигрываете с вероятностью 25%. А с вероятностью 3/4 вы выигрываете при капитуляции! Подробнее об этом в следующем разделе:

Квантовое бессмертие и защита против него

Кнопка Capitulate может быть полезна для защиты от стратегии игры, основанной на т.н. квантовом бессмертии. Остановимся на этом поподробнее.

Рассмотрим вот такую шахматную позицию:

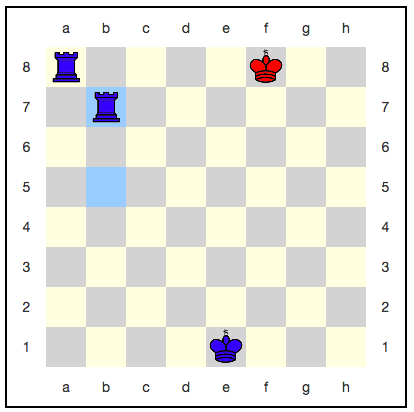
В обычных шахматах это классический мат двумя ладьями. Но в квантовых шахматах не бывает матов, вместо этого нужно съесть короля.

Казалось бы, тут королю некуда отступать: следующим ходом его обязательно съедят. Однако, существует стратегия, использующая квантовое бессмертие: красные могут каждым ходом разбивать своего короля, и он никогда не будет съеден полностью. Например, вот такая последовательность ходов:

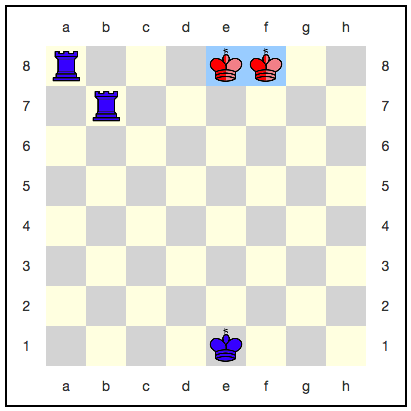
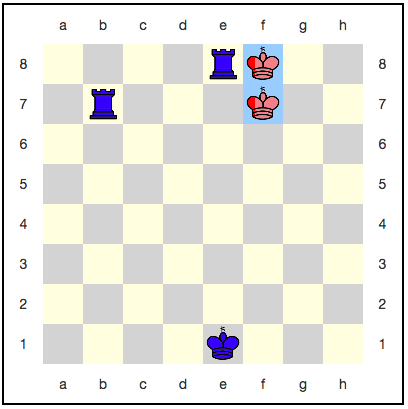
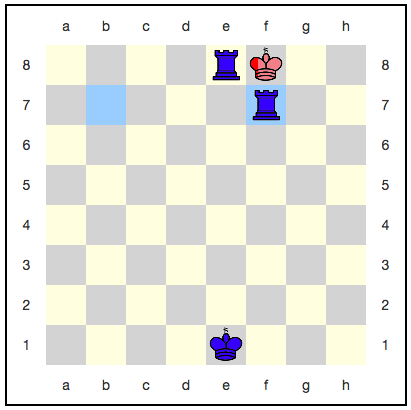
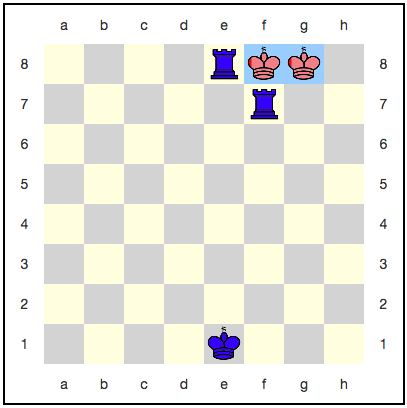
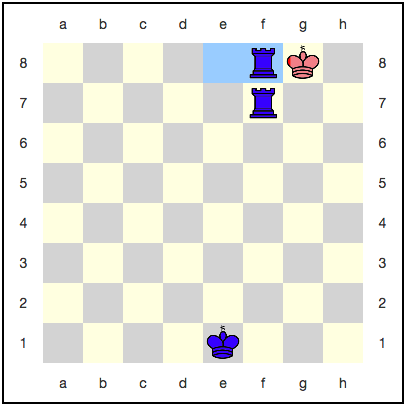
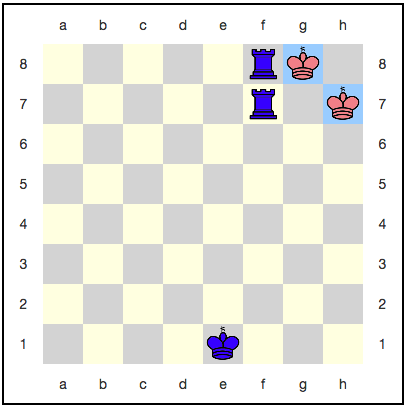
С каждым ходом вероятность выигрыша синих увеличивается, но она никогда не достигнет единицы. Получается, что игра будет идти бесконечно, и синие так и не получат заслуженную победу?

В такой ситуации, как ни странно, полезной оказывается капитуляция. Если вероятность победы синих оказывается равной, скажем, 65535/65536, то можно смело нажимать на капитуляцию. Как написано выше, капитуляция произойдёт только на тех досках из суперпозиции, на которых игра всё ещё идёт. Т.е. синие выигрывают с вероятностью 65535/65536, просто капитулируя!

Ну а если сработает 1/65536… Наверное, это ужасно неприятно 🙂

Коллапс: то самое «взаимодействие с измерительным прибором»

В квантовых шахматах разрешены произвольные суперпозиции фигур. Более того, создавать суперпозиции – это не просто весело: будучи новичком в обычных шахматах и играя против гроссмейстера, можно сильно сгладить его преймущество перед вами при помощи введения доски в сложные суперпозиции!

Однако существуют суперпозиции, которые признаются слишком сумасшедними. Такие суперпозиции не могут существовать; как только они появляются – движок квантовых шахмат запускает механизм разрушения таких суперпозиций, или то самое «взаимодействие с измерительным прибором».

Критерий прост: не могут существовать суперпозиции, в которых одна и та же клетка оккупирована двумя и более фигурами одновременно. Согласитесь, было бы черезчур запутано и сложно, если бы у вас на одной и той же клетке могли находиться конь и вражеская ладья одновременно?

Суперпозиция фигур vs суперпозиция досок

Особого внимания заслуживает процесс разрушения суперпозиций. Мы любом суперпозиции (ради них игра и создавалась), поэтому при коллапсе мы хотим сохранить как можно больше суперпозиций. Например, рассмотрим вот такую ситуацию:

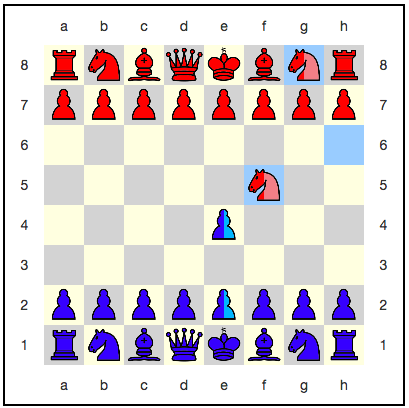
Что произойдёт когда синяя пешка возьмёт красного коня e4:f5?

Одна из распространённых логических ошибок, которую можно совершить в квантовой механике, заключается в недостаточно общем понимании суперпозиций. Если, например, рассуждать с точки зрения отдельных фигур – мол, вот пешка, она находится в суперпозиции – то очень легко завести себя в тупик.

Чтобы этого не происходило, самый верный способ – это помнить, что в суперпозициях находится всегда вся система целиком, т.е. в нашем случае – шахматная доска. Неудивительно что по этому принципу и работает движок квантовых шахмат. Рассмотрим ситуацию выше в представлении движка:

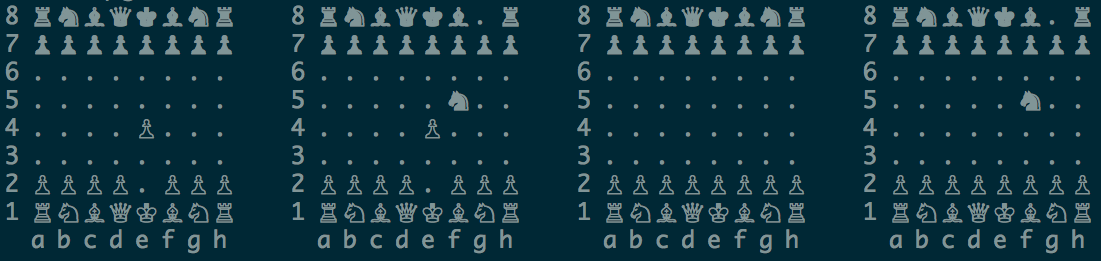
Видно, что движок представляет суперпозицию именно в вышеупомянутом виде: как набор досок. В данном случае возможны 4 показанных выше доски, так как красный конь и синяя пешка могли либо сделать ход, либо нет. Квантовая шахматная доска находится в суперпозиции четырёх обычных досок.

Такое представление более точно, и обеспечивает пользователя полной информацией о квантовом состоянии шахматной доски. В отличии от представления в интерфейсе, которое показывает только вероятности всех фигур. По задумке, игрок должен сам держать в голове квантовое состояние исходя из предыдущих ходов. Умение мыслить в терминах квантовой механики таким образом – сильный козырь в руках игрока в квантовые шахматы.

Минимальный коллапс

На суперпозиции досок хорошо видно, что после хода e4:f5:

1. На первой доске: пешка не сможет сходить по диагонали, т.к. ей нечего есть. Ничего не изменится, на клетка f5 пустая.
2. На второй доске: пешка сможет съесть коня. На клетке f5 пешка.
3. На третей доске: пешки просто нет на e4. Ход не проходит, клетка f5 – пустая.
4. На четвёртой доске: пешки снова нет на e4. Ход не проходит, на клетке f5 остаётся конь.

После применения хода возникает конфликт между конём и пешкой за клетку f5. На второй доске там теперь находится пешка, а на четвёртой – конь.

Как мы уже обговаривали, мы хотим разрешить этот конфликт, при этом разрушив как можно меньше суперпозиций. Поэтому:

• Первая и третья доски не вступают в конфликт ни с кем. Поэтому коллапс не должен их затронуть. Они останутся, и на них продолжится игра.
• Вторая и четвёртая доски конфликтуют между собой. Поэтому между ними при помощи генератора случайных чисел выбирается выживший вариант, с вероятностью 50/50.

Первый вариант: конь выжил

Вторая доска отбрасывается, и игра продолжается на суперпозиции досок с номерами 1, 3, 4:

Заметим, что апостериорная вероятность пешки перераспределилась! Теперь с вероятностью 2/3 пешка находится на e2 (доски 3 и 4), а с вероятностью 1/3 – на e4 (доска 1).

Это правильно! Априори пешка находилась на e2 с вероятностью 50%, но эта вероятность поменялась после генерации случайного числа. Апостериори вероятность стала 66.7%.

То же самое верно и для коня (читатель может подсчитать доски и убедиться, что вероятность нахождения коня на f5 поменялась с 50% до 33.3%).

Вот так результат выглядит в интерфейсе:

Второй вариант: коня съели

Четвёртая доска отбрасывается, и игра продолжается на суперпозиции досок с номерами 1, 2, 3:

В этом случае конь теперь находится в суперпозиции живого и мёртвого, как кот Шрёдингера. А пешка с вероятностью 33.3% размазана по позициям e2, e4, f5. Вот так результат выглядит в интерфейсе:

Квантовая запутанность

Одно из самых известных и захватывающих явлений в квантовом мире – квантовая запутанность. Впервые она была рассмотрена Энштейном в мысленном эксперименте, носящим название ЭПР-парадокс:

Рассмотрим пару частица-античастица, образовавшуюся в процессе распада более тяжёлой стационарной (т.е. покоящейся) частицы, например – мезона. Эйнштейн утверждал, что по закону сохранения импульса – импульсы частицы и античастицы связаны законом сохранения импульса; а значит измерив координату частицы и импульс античастицы можно вычислить при помощи этого закона импульс частицы, а значит – измерить одновременно импульсы частицы и античастицы, т.е. нарушить принцип неопределённости Гейзенберга. Означает ли это, что «квантово-механическое описание реальности не является полным» ©?

Бор предложил разрешение этого парадокса: после измерения импульса частицы импульс античастицы мгновенно изменяет своё значение, а значит её координата оказывается неопределённой. Аналогично, после измерения координаты античастицы координата частицы мгновенно меняет своё значение, а значит импульс оказывается неопределённым.

Какова же природа этого «кошмарного дальнодействия»?

Сейчас достоверно известно, что объяснение Бора верно. Оно оказывается гораздо более логичным и понятным, если перевести его на правильный язык: мы должны делать утверждения о суперпозиции системы частица+античастица, а не о суперпозиции её отдельных компонент.

Рассмотрим эту ситуацию на гораздо более наглядном примере: на квантовой шахматной доске.

Запутанность в квантовых шахматах

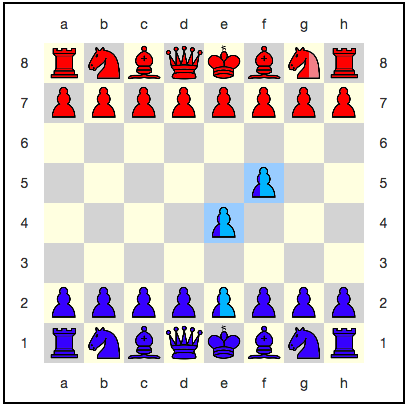
Квантовая шахматная доска позволяет прочувствовать понятие шахматной запутанности. Для того, чтобы перевести доску в состояние шахматной запутанности, нужно… пройти одной фигурой сквозь другую. Рассмотрим пример:

Синие ходят ферзём (королевой) d1:f3. Это – обычный, неквантовый ход! Но он возможен не на всех досках суперпозиции. Посмотрим как ситуация выглядит в представлении движка квантовых шахмат:

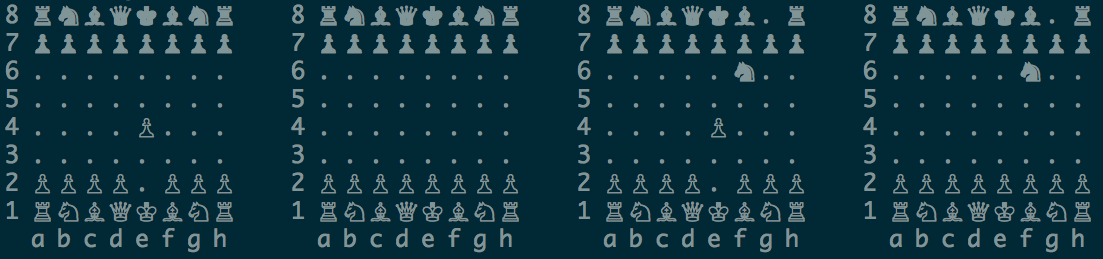
Ход возможен на досках 1 и 3, т.е. на двух досках из четырёх. Поэтому в этом случае обычный неквантовый ход введёт синего ферзя в суперпозицию:

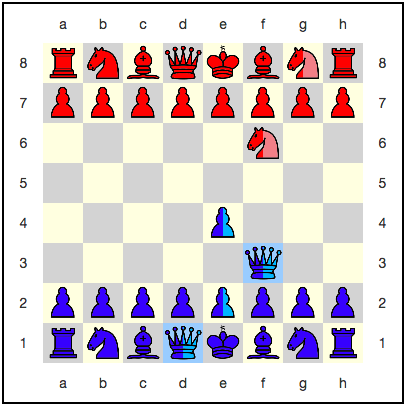
Однако есть кое-что, заметное не сразу. Обратимся к представлению движка:

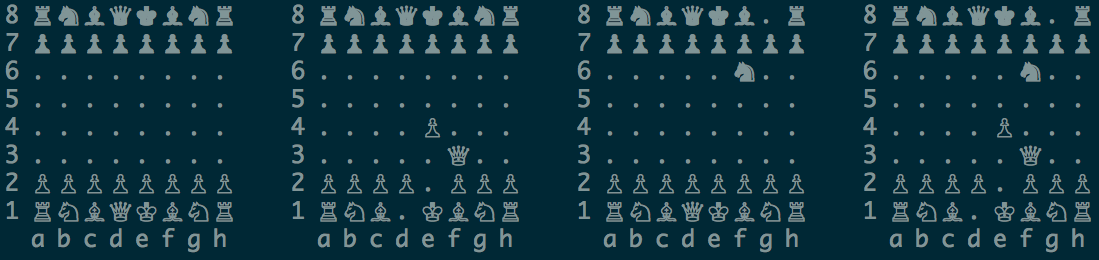
Утверждение: ферзь размазан по позициям d1 и f3 с вероятностями 50%; пешка размазана по позициям e2 и e4 с вероятностью 50%, но при этом выполняется очень важное свойство: если пешка находится на e2, то ферзь – на d1; если пешка на e4 – то ферзь на f3.

То есть положения ферзя и пешки связаны между собой, аналогично импульсам частицы и античастицы в ЭПР-парадоксе. Пешка и ферзь квантово запутаны!

Что это значит и как это можно использовать в игре

Предположим, красные играют конём f6:e4. После разрешения конфликта за клетку e4 предположим, что конь победил. В этом случае выхлоп движка выглядит вот так:

Интересное наблюдение заключается в том, что перераспределение вероятностей пешки (66.7% на e2 и 33.3% съедена) мгновенно повлияло на вероятность ферзя.

Вот так это выглядит в интерфейсе после хода:

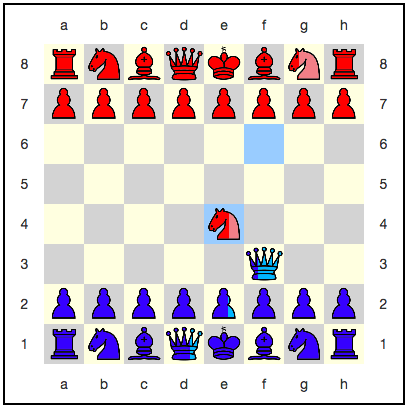
Мы наконец осознали природу того самого «кошмарного дальнодействия» из ЭПР-парадокса. Никакого дальнодействия нету; просто сама система (в нашем случае – шахматная доска) находится в такой суперпозиции, в которой разрешены только варианты с определённой корреляцией двух фигур. Неправильно говорить, что измерение позиции пешки влияет на позицию ферзя. Правильнее говорить, что в суперпозиции есть только такие варианты (шахматные доски), на которых координаты ферзя и пешки связаны вот таким вот соотношением.

Оказывается, что квантовая запутанность – это вполне обычный эффект, который объясняется обычной суперпозицией; но только если не забывать что мы говорим о суперпозиции всей системы в целом, т.е. в нашем случае – шахматной доски, а не обычной фигуры.

Для стратегии игры это означает, что следует следить за ходами и смотреть когда фигуры оказываются в состоянии запутанности. Из интерфейса не очевидно, что фигуры запутаны. Для того, чтобы это понять, нужно знать историю ходов. Такая информация очень важна, т.к. позволяет трезво оценивать вероятности при рассуждении над последующими ходами.

Например, вероятность того, что пешка на e4 и ферзь на f3 смогут вместе поучавствовать в наступлении равна не 25%, как может показаться, а 50%, потому что пешка запутана с ферзём.

Заключение

Ну вот и всё. Надеюсь, у меня получилось наглядно описать принципы квантовой механики и показать их на таком удачном примере как квантовая шахматная доска.

Удачность примера обуславливается двумя свойствами:

1. Шахматная доска – предмет, знакомый почти всем с детства
2. На удивление большинство квантово-механических явлений существуют на квантовой доске

На последок хочется сказать, что движок тщательно протестирован; и хоть в нём и возможны баги, куда вероятнее что он всё подсчитал правильно. Если кажется, что движок неправ – то всегда можно расписать на бумажке квантовую суперпозицию досок в представлении движка и пересчитать вероятности после разрешения конфликта за клетку.

Жду ваших комментариев!