В поиске почти тонкого множества целых

Посмотрите на последовательность числе на картинке.

Какое из чисел, написанных мелким шрифтом, можно превратить в написанное большим шрифтом так, чтобы нигде не образовалась арифметическая прогрессия? 12 мы трогать не можем — сразу образуется последовательность с шагом 1 — 11-12-13. Аналогично 17. 14 и 15 не подходят из-за 11-13-15 и 14-16-18 с шагом 2. Как видите, везде нам грозят ‘вилки‘, и вы будете правы, если предположите, что для бесконечной последовательности целых с ненулевой плотностью на бесконечности — это дело безнадежное. Действительно, в таких последовательностях всегда имеется произвольное количество арифметических прогрессий, причем произвольно большой длины.

А вот что интересно — так это то, что условие положительной плотности не является необходимым — если множества целых нулевой плотности, обладающие тем же свойством! Одну такую последовательность вы хорошо знаете — это множество простых чисел. Доказано, что во множестве простых чисел можно найти прогрессии любой длины — хотя практически самая длинная из найденных численно составляет 27 элементов.

Тем не менее несложно придумать бесконечную последовательность, которая точно не содержит ни одной арифметической прогрессии. Вот она: 1, 10, 100, 1000, 10000 итд. Эта последовательность с нулевой плотностью, и она, неформально говоря, уж совсем быстро сходит ‘на нет’, она куда более ‘рыхлая’, чем множество простых чисел. Но есть ли какой-либо формальный критерий этой рыхлости?

Гипотеза Пола Эрдоша

Великий Пол Эрдош (вы, разумеется, знаете кто это? если нет, то срочно в Вики), сгенеривший более тысячи гипотез, предложил такой критерий для определения типа множества. Кстати, множества, где нет бесконечного количество прогрессий мы будем называть ‘тонкими’ (thin set), а их противоположности — ‘большими’ (large set) :

Итак, если сумма обратных величин расходится, то множество large, иначе thin:

Для простых чисел эта сумма, как известно, расходится (хотя и растет очень медленно — как log(log(n)), а вот для нашей ‘тонкой’ последовательности мы получим 1.1111…

Предположение Эрдоша доказано лишь недавно (в 2020 году) и лишь частично: доказано, что в большом множестве будет бесконечное число прогрессий из трех элементов (но не доказано, что там будут прогрессии любой длины). Однако поверим интуиции Эрдоша — она его подвела по-крупному лишь однажды — с парадоксом Монти Холла.

Давайте теперь возьмем последовательность простых чисел «близнецов»: (3,5), (5,7), (11, 13), итд. Чисел близнецов меньше и… сумма обратных величин сходятся к константе Бруна 1.902160583104… Эта константа известна довольно приближенно — даже после суммирования обратных для более миллиарда пар близнецов ошибка составляет около 5% (поэтому приведенное число есть результат аппроксимации того, скак сходится сумма — то есть дорисовали график карандашом).

Забавно, что не доказано до сих пор, что чисел близнецов бесконечное количество, хотя это скорее всего так. Но в любом случае их плотность падает так быстро, что критерий Эрдоша указывает, что множество близнецов тонкое.

Так где же граница?

Возникает закономерный вопрос: если плотность множества простых падает как log(x) и это множество ‘большое‘, а плотность множества близнецов падает как log(x)^2 и уже ‘тонкое‘, то где же граница? Что если мы добавим дополнительное решето (sieve), которое будет оставлять лишь некоторые простые? Например, так:

  #
  sieve += 1.0/F(p)
  if sieve>=1.0: 
    sieve -= 1.0
    sum_sieve += 1.0/p
  # 

Где F(p) — функция ‘решета’. Например, если F(p)=10, то sum_sieve будет суммировать лишь каждое 10е число. Время численного эксперимента, разомнем ручки и посчитаем простые до 2 миллиардов:

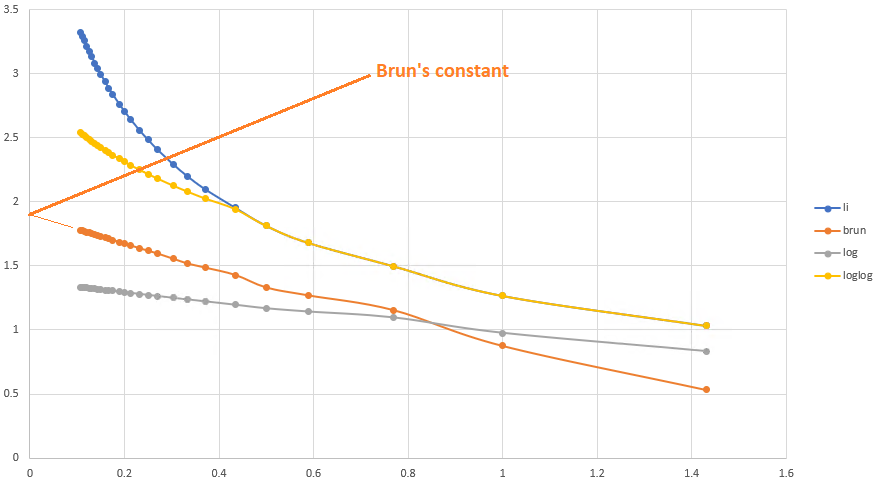
На графике y это сумма, а вот ось х подана как обратная к логарифму, x=1/log(p). Это переносит бесконечность в точку 0 и становится более понятным поведение суммы обратных при росте p.

Синяя кривая (li) это сумма обратных ко всем натуральным числам. Она растет как логарифм. Желтая log — сумма обратных к простым, она растет как log(log(p)). Наконец, серая это дополнительное решето F(p)=log(p), это решето слишком ‘сильное’ и делает последовательность ‘тонкой’. Как найти золотую середину?

Аналитический подход

Воспользуемся тем, что сходимость/расходимость обратной суммы совпадает с тем, сходится ли интеграл:

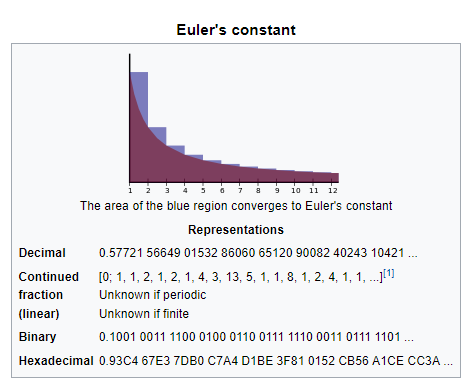
Где F(x) — функция дополнительного решета (на самом деле можно применять решето не к простым, а вообще ко всем числам — ‘сила’ решета простых это дополнительные log(x)). Для просто набора целых и интеграл 1/x, и сумма 1/n расходятся, но вот их разность конечна и стремится к константе Эйлера:

Итак, сумма обратным к простым растет как log(log(p))? Ослабим этот рост решетом такой же силы!

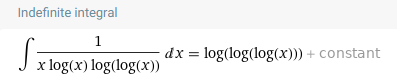
Вау! теперь рост медленнее — как тройной логарифм. Но все таки бесконечный рост. Может поиграем степенью у двойного логарифма в знаменателе? Например, уcилим решето:

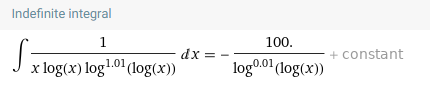
При сколь угодно малом превышении степени 1 у логарифма множество становится тонким, интеграл сходится. А если степень сделать меньше 1, например, 0.99:

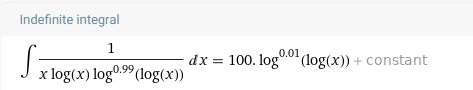
и мы возвращаемся к более быстрому росту двойного, а не тройного логарифма. Поиграем степенью при логарифме (pwr) и построим графики:

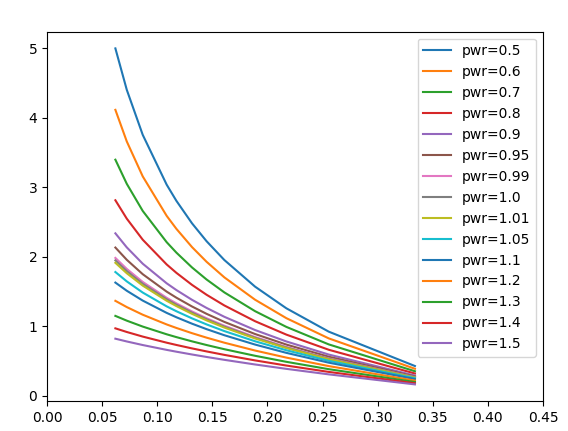
И все же, где граница?

Как мы видели, степень при последнем члене работает слишком топорно. Что если мы поступим как раньше — если есть рост тройного логарифма, то добавим его в решето:

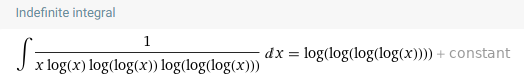
Получаем еще более медленный рост — четверной логарифм! Но главное, так можно делать до бесконечности, определив знаменатель как:

При этом степень при логарифме означает кратность применения логарифма (как в теории быстрорастущих функций), а не возведение в степень (вообще странно, что в математике сохранилась такая синтаксическая двусмысленность). Мы из лени писать длинный latex считаем, что min будет ловить exceptions от отрицательных логарифмов.

Тут бы показать вам красивые графики, но рост нашей медленной функции столь медленен, что:

• делитель log(log(p)) вступает в силу при e**e = 15.15…

• log(log(log(p))) при 3814279

• Логарифм четвертой кратности, очевидно, при e**3814279, а это слишком больше число

Так что красивого веера графиков, увы, не получить. Но граница нащупана — мы получили бесконечно медленно растущую функцию. Похоже, на каждом ‘этапе’ (e, 15, 3814279, e**3814279, …) она будет возрастать на небольшую величину (примерно константу), а связанное с ней множество целых будет ‘почти тонким’