Предисловие
В физике часто оперируют волновыми функциями с ярко выраженными свойствами частиц. Давно стали обыденными понятия частиц с положительным и отрицательным зарядами, с соответствующим взаимодействием. Часто используют Лоренц-преобразования, когда при увеличении скорости волна-частица сжимается, с соответствующим увеличением полной энергии при приближении к скорости света.
Но можно ли представить простейшую и наглядную модель, из которой выводятся все эти свойства разом?
Одной из таких моделей является модель Френкеля-Конторовой, которую мы рассмотрим в рамках истории теории солитонов.
Структура статьи: во введении напомним, как открыли солитоны в 1950-1960-х годах используя компьютеры. Потом расскажем о самой модели и её свойствах. В третьем разделе рассмотрим ее в контексте развития ранней истории солитонов. Мы будем излагать вопрос, разумеется, упрощённо, но наглядно: продемонстрируем поведение модели с помощью её реализации на WebGL.
Введение
На моей книжной полке стоит с десяток книг о солитонах, и в каждой из них Джон Скотт Рассел скачет на лошади за движущейся по каналу «волной трансляции», как он назвал будущий солитон. Трудно удержаться в книге о солитонах, чтобы не воспроизвести поэтическое описание первооткрывателя, но вместо этого упомяну о фактах, менее известных.— Наянов В. И. [1]
Моя статистика такова: из стоящих на полке книг, которые посвящены именно теории солитонов, Джон Скотт Рассел скачет в восьми [1-8]. А в остальных пяти [9-13] не скачет, и авторы сразу переходят к рассматриваемым темам. Джону Расселу отдают дань не только как первооткрывателю уединенных волн, но и в качестве примера превратностей научных идей.
Теория солитонов развивалась волнами, идеи то забывались на десятилетия, то неожиданно проявлялись в смежных областях, то переоткрывались вновь. Мы же опустим эту историю, воспользуемся тем, что в научно-популярной монографии А. Филиппова [3] история наблюдения волны трансляции описана очень подробно, а также тем что, на «Хабре» уже была статья с упоминанием Рассела на лошади (‘Парадокс, положивший начало научным вычислениям’) об эксперименте ФПУ, проведенном Энрико Ферми, Джоном Паста, Станиславом Уламом и Мэри Цингу на одном из первых компьютеров MANIAC в Лос-Аламосской национальной лаборатории.
Вкратце напомним некоторые моменты из той статьи, которую можно считать «нулевой» частью данного цикла.
Авторы эксперимента задались вопросом «почему теплопроводность конечна» и подчиняется феноменологическому закону теплопроводности Фурье. За два столетия так и не удавалось вывести его из основополагающих физических законов.
В простейшем случае, если моделировать среду или атомы как цепочку грузов связанных пружинами, система будет подчиняться волновому уравнению () хорошо описывающему распространение звука, колебания струны или плоских электромагнитных волн. Согласно уравнению возмущения распространяются со скоростью звука не меняя своей частоты, а энергия беспрепятственно переносится независимыми модами, эффективная теплопроводность бесконечна, для передачи тепла с одного конца на другой не нужен перепад температуры и уравнения диффузии тепла не получается. В наблюдаемой же физической реальности, например, в металлах скорость звука может достигать километров в секунду, однако их теплопроводность конечна.
В 1910-х годах Петер Дебай высказал гипотезу, что конечная теплопроводность возникает из-за нелинейности. Поэтому в эксперименте ФПУ, проведенном в 1949 году [14], численную модель составили из пружинок, которые не подчиняются строго линейному закону Гука (, его проходят в школе). К упругим силам добавили нелинейность второго и третьего порядка:
. Предполагалось, что из-за слабой нелинейности первоначальное возбуждение равномерно распределится по остальным колебательным модам и приведет к белому шуму. И первые результаты моделирования вполне соответствовали гипотезе. Но однажды из-за затянувшегося обеденного перерыва компьютер оставили работать дольше обычного, и ученые заметили, что моделируемая система из хаотического теплового равновесия вернулась почти в исходное состояние, с точностью до двух процентов.
Далее в 1965 году М. Д. Крускал и Н. Забуски (между прочим один из авторов упомянутой выше переведенной на «хабре» статьи) открыли [15], а точнее переоткрыли, уравнение Кортеверга-де Фризом (КдФ) выведенное физиком Кортевергом и студентом де Фризом ещё в 1895 году:
где — функция от времени
и координаты
, а индекс обозначает переменную по которой берется частная производная.
Данное уравнение описывает солитоны распространяющиеся только в одном направлении. Оно получается когда пружины имеют нелинейность 2-го порядка (). В случае же нелинейности пружин в третьем порядке (
) получается модифицированное уравнение КдФ (мКдФ)
[6, стр. 35]. При этом нас не должно смущать число 6, такой коэффициент выбран лишь для удобства последующих вычислений. Уравнение может быть записано с произвольным коэффициентом путем изменения масштаба заменой переменных (
).
Волны трансляции в виде движущегося с постоянной скоростью профиля (обычно в виде горба), который сохраняет свою форму, существуют у многих уравнений. Но для уравнения КдФ Крускал и Забужский путём численного моделирования обнаружили, что волны сохраняют форму устойчиво и сталкиваются упруго (эффект, совершенно не характерный для линейных волн): при столкновении двух или нескольких волн-горбов (например, когда более быстрая волна догоняет медленную), после взаимодействия они восстанавливают свою форму. Получается, что волна обладает свойством частицы. Поэтому они и назвали такие волны «солитонами».
В следующих статьях цикла о солитонах мы будем рассматривать уравнение КдФ подробней, а здесь пока что приведем формулу односолитонного решения.
Формула решения уравнения КдФ соответствующая солитону
,
где — параметр который определяет скорость солитона (
) и амплитуду, т.е. высоту горба (
), а
— гиперболический косинус.
Решение отрицательно лишь в силу выбора знака , подразумеваемого формой уравнения. Масштабное преобразование
приводит к другой форме уравнений КдФ:
с решением типа уединенной волны
Можно удостовериться, что при подстановке данного решения уравнение КдФ выполняется. Например, проведя выкладки вручную требуется лишь вспомнить о дифференцировании, свойствах гиперболических функций и упрощения выражений. Или решение можно проверить с помощью системы символьных вычислений (системой компьютерной алгебры). Можно проверить численно используя разностные схемы.
Модель Френкеля-Конторовой
Описание модели
В 1939 году Я. И. Френкель и Т. М. Конторова задались вопросом, как можно промоделировать дефекты в слое атомов и какие получатся у них свойства.
Самая простейшая модель строения большинства твердых тел имеющих кристаллическую структуру состоит из решетки (в одномерном случае из цепочки) атомов или йонов, соединенных друг с другом воображаемыми пружинами.
Френкель и Конторова ее модифицировали добавив воздействие подложки состоящей из слоя неподвижных атомов расположенных ниже с расстоянием между ними как у верхнего слоя. Такое воздействие можно представить «гофрированной» периодической функцией состоящей из ряда впадин и холмов (горок) в гравитационном поле сил тяжести изображающей потенциальные локальные ямы. То есть в цепочке шариков-пружинок введена нелинейность другим способом нежели в модели ФПУ: пружины остаются линейными, зато добавляется нелинейная периодическая сила (зависящая от смещения как sin).
При невозмущенном состоянии (называемом вакуумным или «нулевом») в центре каждой впадины находится только одна частица. Пружины растянуты одинаково, их воздействие на частицы равны с обоих сторон и противоположены, значит суммарное воздействие пружин равно нулю. Горизонтальное действие гравитационного потенциала внизу ямы тоже равно нулю, так как уклона в центре ямы нету.

В возмущенном состоянии некоторые атомы или ионы могут покидать узлы решетки и блуждать по кристаллу, а их место становится вакантным, т. е. пустым. Эти вакансии можно рассматривать как своего рода «отрицательные атомы» и они могут перемещаться по кристаллу подобно частице. Подобное рассмотрение было применено Полем Дираком в 1928 г. для создания теории антиэлектронов, т. е. позитронов, а впоследствии идея о вакансиях-дырках получила применение и в теории полупроводников.
А дефекты в модели Френкеля-Конторовой (ФК) с периодическим потенциалом получаются следующим образом. Возьмемся за одну частицу-грузик и перекинем ее на чужое место ненадолго удерживая для затухания колебаний остальных частиц. Положение грузиков изменится и система перестроится в другое состояние, в котором остальные грузики будут смещены, и кроме силы пружин на них будет действовать сила зависящая от их конкретного положения на участке между впадинами и холмами.
Вообще говоря таким образом образуются два дефекта, но мы представим, что похожими манипуляциями один из них можно отодвинуть далеко в сторону, в бесконечность. И рассмотрим только один дефект типа «разряжение», когда в некоторой области часть пружин растянута длиннее чем в вакуумном состоянии. Причем в этой системе из-за действия пружин и периодического потенциала не может быть просто «дырки», т. е. не может случиться так, чтобы одна ямка была пустой, а во всех остальных атомы лежали бы на дне. Вместо этого установится конфигурация изображенная на рисунке.
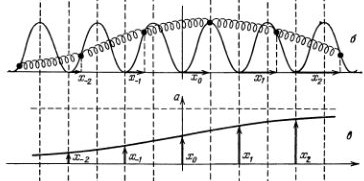

Это и есть дислокации Френкеля-Конторовой. Такая конфигурация называется по договоренности положительной дислокацией или кинком. На всякий случай заметим, что у разных авторов договоренность о знаке может отличаться: [16, стр. 190] отрицательная, [3, стр. 155] положительная.
На рисунке выше видно, что, например, частица 1, смещенная на величину удерживается несколькими силами. Так как она находится не в яме и не на горке (как, например, частица с индексом 0), а на наклонном участке потенциала, то на нее во первых действует сила в сторону ямы, с величиной горизонтальной проекции
, а компенсация удерживающая частицы от падения вызвана разницей в натяжении соседних пружин.
В предельном случае, когда пружинки очень мягкие, дислокация ФК превращается в «дырку» по Френкелю.
Противоположенный тип дислокации получается, когда в некоторой области образовывается сгущение частиц, а пружины сжаты.
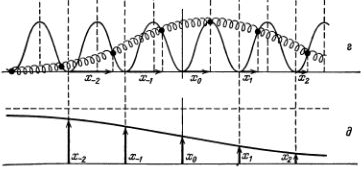

Такая дислокация сгущения называется отрицательной, или антикинком.
Заметим, что в настоящей модели ФК нет материальных впадин и горок, на рисунках они лишь символизируют периодический потенциал воздействия от подложки неподвижных нижележащих атомов. Принимается, что частицы двигаются не по горкам и холмам, а строго горизонтально, без вертикального смещения. Это важно для аналитического вывода уравнения.
Вывод уравнения
Именно уравнение задает эволюцию во времени состояния системы, определяет как будет происходить её развитие, когда известны начальные условия. Если предоставить все данные о состоянии всех объектов, в данном случае положения шариков и их скорости, то уравнение расскажет, что произойдет в будущем. Например, переведя связи, которое заданы уравнением между предыдущем и следующим состоянием, в некоторый алгоритм, можно запустить на компьютере численный расчет. Или из уравнения можно найти некоторые простые частые решения и определить их свойства и эволюцию систему аналитически. Еще можно рассматривать уравнение, вместе с дополнительными данными, что оно однозначно задает статический блок, в котором уже содержится будущее и прошлое. В любом случае математическая формулировка модели в виде уравнения важна.
Уравнение может следовать из описания и представлений о грузиках, пружинах, со строгой логикой, ассоциативно или интуитивно. Но оно вполне может существовать и самостоятельно, без механических представлений. Здесь мы выведем уравнения основываясь на описании приведенном в предыдущем разделе.
Так вот, пусть отклонение i-й частицы от центра ямы задается . Периодическая сила от подложки, вызванная уклоном потенциала в виде представляемых впадин и горок, задается функцией
, Значит на частицу действует сила
, которая при малых отклонениях стремится возвратить частицу к центру ямы. Кроме того на нее действуют силы пружин, пропорциональные жесткости пружины
и ее растяжению. Правая пружина натянута с силой равной
, а левая c силой
. По второму закону Ньютона ускорение частицы зависит от суммы сил, таким образом модель описывается системой из уравнений соответствующих каждой частице
Если бы не было пружин, то каждая частица подчинялась бы уравнению маятника.
А если бы не было впадин, и на частицы действовали только пружины, тогда получили бы линейную систему, в которой волны распространяются со скоростью зависящей от массы частиц и жесткости пружин.
Теперь перейдем к непрерывному пределу, когда расстояния между атомами устремим к 0. В таком пределе силы каждой пружин будут переходить в производную по
. Разница силы — во вторую производную. Система уравнений переходит в уравнение в частных производных:
Сейчас оно известно как уравнение Синус-Гордона (СГ). Так его шутливо назвал один из исследователей, поскольку оно является частным случаем обобщенного уравнения Клейна-Гордона . Точнее, Рубинстейн [17] приписывает авторство этого наименования Крускалу; Колеман [18] утверждает иное, и сам Крускал в этом «не вполне уверен». Так или иначе, но название прижилось в литературе, а потом и вовсе стало официальным [2, стр. 25].
Что касается уравнения Клейна-Гордона, оно было выведено независимо друг от друга Оскаром Клейном [19] и Уолтером Гордоном [20], которые надеялись, что их уравнение будет описывать электроны. Это не так, но оно описывает массивные элементарные частицы без спина, такие как пион или бозон Хиггса.
Вывод уравнения в литературе: [16, стр. 190], [3, стр. 181], [5, стр. 460.
Кинки
Из уравнения СГ следует, что покоящаяся дислокация удовлетворяет обыкновенному дифференциальному уравнению (ОДУ):
которое (при замене пространственной переменной на временную
) похоже на уравнение математического маятника , только вместо пространственной переменной
описывает поведение единственного маятника во времени
.
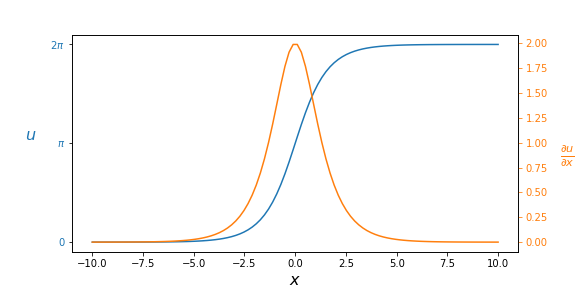
Стационарное односолитонное решение уравнения СГ задается формулой
где — произвольный параметр, который задает положение центра дислокации. Данное решение соответствует так называемой сепаратисе математического маятника.
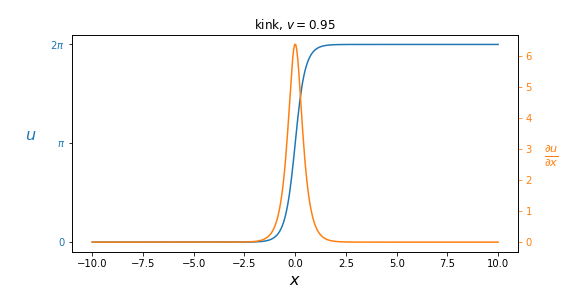
А в модели ФК оно соответствует разряженной дислокации. Данный тип решения также называют «кинком» от слова «изгиб», так как график функции покоящегося солитона выглядит как сигмоид, Еще его называют — импульсом, так как значение функции изменяется на эту величину на прямой
от
до
.
Дислокации могут перемещаться. В модели мы не вводим диссипативные силы (силы трения), поэтому отдельные дислокации могут двигаться с постоянной скоростью.
Формула решения в виде «кинка» движущегося со скоростью :
где
— коэффициент «сжатия» солитона, который зависит от скорости
— задает начальное положение середины солитона в момент времени
с точностью до константы сжатия:
В отличии от модели КдФ некоторые солитоны могут обладать свойством «заряда». Отрицательные дислокации, или антикинки, или — импульс, задаются похожей формулой, но только с измененным знаком.
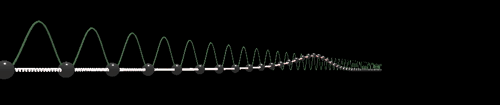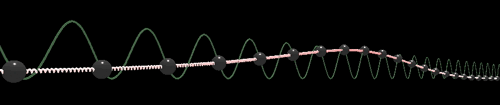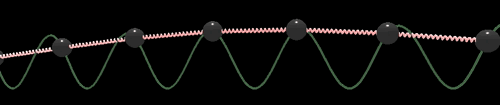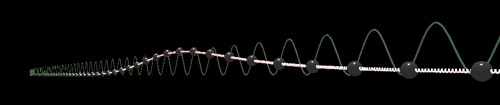
Реализация «кинка» и «антикинка» на WebGL выглядит следующим образом:
WebGL: Кинк
По данным ссылкам на реализацию WebGL можно играть параметрами движения и визуализации. Из формулы решения видно, что при движении со скоростью Тогда кинк движущийся, например, со скоростью 0,95% от скорости «света» Сжатие движущегося кинка относительно покоящегося напоминает преобразование длин при переходе в движущуюся систему координат в специальной теории относительности. Рассмотрим свойства, которые вытекают из формул решений. Найдем полную энергию покоящегося кинка Теперь можно определить «массу покоя» и сравнить ее с полной энергией движущегося. Получим: Таким образом быстро движущиеся дислокации подчиняются не механике Ньютона, а механике специальной теории относительности. При малой скорости движения дислокации Решение типа кинк подробней рассмотрено в литературе на страницах: [3, стр. 176], [5, стр. 26], [8, стр. 86], [21, стр. 27], об энергии и импульсе движущегося кинка: [16, стр. 196], [3, стр. 177], [5, стр. 438], [10, стр. 215]. Мы же далее приведем общие соображения о Лоренц-преобразованиях применительно к данной модели. Уравнения вида обладают лоренц-ковариантностью (двумерной, то есть по переменным Другими словами, если другое решение Однако не для любой функции В данном случае Лоренц-преобразования демонстрируют вот что: есть решение в одном пространстве В быту мы привыкли, что наблюдатель своими средствами наблюдения (глазами с помощью света, то есть электромагнитных волн) не оказывает влияния на объекты обычной механики (столкновение шаров, звуковые волны) находится в стороне, так как сделан из вещества в быту мало связанного с электромагнитными волнами. Остальные нюансы споров об эфире и СТО мы здесь рассматриваем не будем. Что касается кажущейся выделенной системы отсчета для скорости света (наблюдаемое отсутствие анизотропности, проблема односторонности скорости света), то, возможно, её не получается обнаружить из-за эффектов преобразований Лоренца и СТО, которым подчиняется уравнение СГ. В отношении обобщенного уравнения Клейна-Гордона в так называемых конусных переменных [2, стр. 15]
Крускалл сделал полезное замечание, что данное уравнение всегда обладает одной сохраняющейся плотностью, которую можно записать в виде полинома от Тривиальный закон сохранения (в виде уравнения непрерывности) записывается как где плотность заряда Эти уравнения никак не связаны с динамикой и попросту накладывают на Кроме законов сохранения соответствующих сохранению энергии и импульса [2, стр. 27], у уравнения СГ имеется еще одна сохраняющаяся величина называемая топологический заряд [5, стр. 441], [8, стр. 86]. Для решения уравнения СГ с закрепленными на бесконечности концами величина сохраняется во времени. Теперь рассмотрим взаимодействия нескольких дислокаций в модели Френкеля-Конторовой. Интуитивно можно понять, что одна дислокация будет действовать на другую. Психологически легче понять, как отталкиваются две антидислокации, в которых пружинки сжаты. Но и две дислокации с растянутыми пружинками отталкиваются точно также. А положительная и отрицательная — «притягиваются». В аналитическом же виде, то есть в виде формул, нахождение многосолитонных решений для нелинейных уравнений является нетривиальной задачей. Для нелинейных уравнений суперпозицию решений применять неверно. Мы не можем просто взять два известных решения и сложить их. Например для квадратичного члена в общем случае И тоже самое касается нелинейной функции В 1962 г. Перринг и Скирме нашли, а точнее угадали, двухсолитонное решение уравнения СГ с помощью численных экспериментов [22], [5 стр. 26], [2 стр. 21], [8 стр. 92], [23 стр. 1]
где В реализации модели ФК на WebGL столкновения выглядят следующим образом: Еще одним интересным типом решений уравнения СГ является солитонный «атом» называемый бризер). При достаточно близком начальном расположении кинка и антикинка они могут образовать некоторую связанную, неразлучную пару, нечто вроде атома водорода (или, скорее, «атома» позитрония, т. е. атома водорода, в котором протон заменен на позитрон). Силы притяжения между взаимно отрицательными частицами не дают им разделиться, но, в отличии от реальных позитрона и электрона, в модели СГ не может происходить аннигиляции. вместо этого бризер ведет себя как пульсация. Для безразмерного уравнения СГ ( с параметром В реализации на WebGL этот параметр также можно изменять: Заметим в отличии от пары позитрон-электрон, которые могут анигилировать при столкновении, в модели Френкеля-Конторовой положительные и отрицательные дислокации в связанном состоянии могут находиться бесконечно долго. [3, стр. 167]
Другая удивительная особенность этой стоячей волны состоит в том, что она тоже ведет себя как частица, бризер может равномерно двигаться, а кинки проходить через него. Бризер движущийся со скоростью где Лоренц-фактор В заключении снова вернемся к 1960-м годам, чтобы иметь преставления об истории других солитонных уравнений. Если раньше казалось, что уравнения делятся на две основные группы: линейные уравнения, у которых имеется простой методы решений, и нелинейные практически нерешаемый, то теперь начали появляться классы нелинейных интегрируемых уравнений, у которых есть некоторые общие свойства и способы их решений. Сначала некоторые законы сохранения были открыты для уравнения КдФ. Первоначально смысл в поиске законов сохранения состоял в том, что с их помощью можно попытаться описать решения уравнения КдФ на скачках в области резких изменений решения. Способ аналогичный задачам в газовой динамикой при прохождении ударной волны или аналогичный способ в механических задачах, в которых законы сохранения помогают найти состояние после упругих или неупругих соударений ). Также законы сохранения имеют значение для интегрируемых систем. Потом оказалось что у уравнения КдФ их бесконечное число, и что они играют ключевую роль в открытии метода решений с помощью обратного преобразования рассеяния. Миура обнаружил, что бесконечное число законов сохранения имеется также и у модифицированного уравнения КдФ (мКдФ). Более того, он нашел преобразование как из решения уравнения КдФ получить решение уравнения мКдФ. Преобразование Миуры оказались основополагающим для открытия метода обратной задачи рассеяния Гарднеру, Крускалу и Миуре [25] нашли, что собственные значения оператора Шредингера А в 1967 году Гарднером, Грином Крускулом и Миурой был открыт так называемый метод обратного преобразования рассеяния (ОПР) для уравнения КдФ, в котором используется в некоторым смысле «нелинейное преобразование Фурье». Метод называется так поскольку в нем используется решение задачи квантовой механики о восстановлении потенциала по данным рассеяния потенциала. В русскоязычной литературе его принято назвать «метод обратной задачи рассеяния» (МОЗР) Многие воспринимали результаты по КдФ как трюк… Однако в 1971 году В. Е. Захаров и А. Б. Шабат нашли пару Лакса и применили метод обратной задачи для нелинейного уравнения Шрёдингера. Вскоре М. Вадати, используя идеи прямой и обратной задачи рассеяния, предложил решение модифицированного уравнения Кортевега — де Фриза (мКдФ) Затем М. Абловиц, Д. Кауп, А. Ньюэлл и Х. Сигур (АКНС), руководствуясь несколькими ключевыми наблюдениями Крускала, решили уравнение синус-Гордона (независимо решенное Лэмом и, несколько позднее, Фаддеевым и Тахтаджяном) и вслед за этим предложили способ, как выписывать полный набор уравнений (АКНС-иерархия). По всему миру начался так называемый солитонный бум 1970-х годов… В данной статье мы рассмотрели только основные свойства модели ФК в рамках теории солитонов, которая является одномерной. Интересно было бы узнать о ее многомерных обобщениях. Но так как направления расширения зависят от кругозора, желательно узнать о других не менее интересных моделях и уравнениях, а также иметь представления о путях, находках, тупиках теории солитонов. В. И. Наянов, Многополевые солитоны, Москва: Физматлит, 2006. Р. Буллаф, Ф. Кодри, Солитоны, Мир, 1983. А. Т. Филиппов, Многоликий солитон, 2 edition, Издательство: Наука, Физматлит, 1985, Серия: Библиотечка «Квант», 1990. М. Абловиц, Х. Сигур, Солитоны и метод обратной задачи, Москва: Мир, 1987. Р. Додд, Д. Эйлбек, Д. Гиббон, Х. Моррис, Солитоны и нелинейные волновые уравнения, М.: Мир,, 1988. А. Нюэлл, Солитоны в математике и физике, Москва: Мир, 1989. А. Дегасперис, Ф. Калоджеро, Спектральные преобразования и солитоны. Методы решения и исследования нелинейных эволюционных уравнений, Москва: Мир, 1985. В. Ю. Новокшенов, Введение в теорию солитонов, Москва : Ин-т компьют. исслед, 2002. В. Е. Захаров, С. В. Манаков, С. П. Новиков, Л. П. Питаевский, Теория солитонов: Метод обратной задачи, Москва: Наука, 1980. Р. Раджараман, Солитоны и инстантоны в квантовой теории поля, М: Мир, 1985. Л. А. Тахтаджян, Л. Д. Фаддеев, Гамильтонов подход к теории солитонов, Главная редакция физико-математической литературы издательства «Наука», 1986. О. И. Богоявленский, Опрокидывающиеся солитоны, Москва: Наука, 1991. Т. Мива, М. Джимбо, Э. Датэ, Солитоны: дифференциальные уравнения, симметрии и бесконечномерные алгебры, МЦНМО, 2005. A. Fermi, J. Pasta, S. Ulam, Studies of Nonlinear Задачаs.I., Los Alamos Report, LA, pp. 978-988, 1955. N. J. Zabusky, M. D. Kruskal, Interaction of «Solitons» in a Collisionless Plasma and the Recurrence of Initial States, Physical Review Letters, 15(6), pp. 240-243, doi: «10.1103/physrevlett.15.240», 1965. Д. Л. Лэм, Введение в теорию солитонов, М.: Мир, 1983. J. Rubinstein, Sine-Gordon Equation, Journal of Mathematical Physics, 11(1), pp. 258-266, doi: «10.1063/1.1665057», 1970. S. Coleman, Classical Lumps and Their Quantum Descendants, in New Phenomena in Subnuclear Physics, pp. pp. 297-421, 1977. O. Klein, Quantentheorie und funfdimensionale Relativitatstheorie, Zeitschrift fur Physik, 37(12), pp. 895-906, doi: «10.1007/bf01397481», 1926. W. Gordon, Der Comptoneffekt nach der Schrodingerschen Theorie, Zeitschrift fur Physik, 40(1-2), pp. 117-133, doi: «10.1007/bf01390840», 1926. S. Cremonesi, C. Sleight, Solitons III, 2022, unpublished. J. K. Perring, T. H. R. Skyrme, A model unified field equation, Nuclear Physics, 31, pp. 550-555, doi: «10.1016/0029-5582(62)90774-5», 1962. A. D. Polyanin, Exact Solutions, Sine-Gordon Equation, 2004. П. Д. Лэкс, Интегралы нелинейных эволюционных уравнений и уединенные волны, Математика, 1969. R. M. Miura, C. S. Gardner, M. D. Kruskal, Korteweg-de Vries Equation and Generalizations. II. Existence of Conservation Laws and Constants of Motion, Journal of Mathematical Physics, 9(8), pp. 1204-1209, doi: «10.1063/1.1664701», 1968. А. Н. Борисов, И. С. Мамаев, Современные методы теории интегрируемых систем, Москва : Ин-т компьютер. исслед., 2003.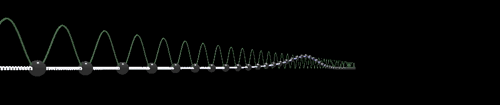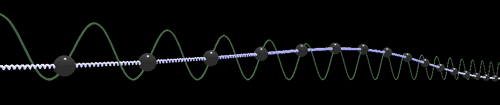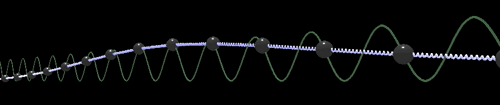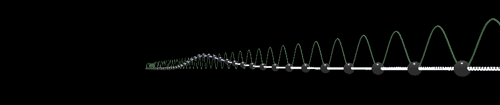
солитон сжимается в
раз по сравнению с покоящимся. Пусть покоящийся кинк имеет условную ширину около 5, которая получается, если его границами считать отклонение
на 5% по формуле
,
будет сжат примерно в
раза и иметь ширину около 1,6.
. Для этого проинтегрируем энергию сжатия всех пружин
и потенциальную энергию смещения
.
кинка
можно пользоваться обычной релятивистской теорией.
Лоренц-ковариантность
). Это означает, что какое-либо решение уравнения после применения к нему преобразования так же будет становиться решением, то есть тоже подчиняться уравнению.
является решением уравнения, то при преобразованиях
также будет подчиняться уравнению
уравнения будут иметь солитонные решения, случай уравнения СГ, когда
выделяется. Всевозможные функции, при которых обобщенное уравнение Клейна-Гордона обладает солитонными свойствами мы выпишем в другой раз при рассмотрении методов решений.
, а есть соответствующее ему через преобразования Лоренца решения в другом пространстве
. То есть мы как бы расположили на столе две модели, каждое со своим решением. Само пространство
при этом не «сжимаются», как и время
. Между тем движущийся солитон будет сжат по сравнению с покоящимся, а тиканье «атома» при его движение может замедлиться. При этом воображаемый наблюдатель, допустим, состоящий из «атомов» в пространстве
, никаким образом не может наблюдать своими средствами, что происходит в расположенной по соседству другой модели. Понятия «наблюдатель» имеет точно определенный смысл при преобразовании Галилея, то есть при описании механических систем таких как движущийся корабль или поезд, в которых средства наблюдения (световые волны) находятся вне модели. Другими словами парадоксы СТО не являются чистым следствием Лоренц-ковариантности (в преобразованиях Лоренца нет наблюдателя, который мог бы наблюдать другое пространство).
Законы сохранения уравнения СГ
и её производных, но необходимое и достаточное условие существования второй полиномиальной сохраняющейся плотностью является выполнение соотношения
и тогда оказывается, что имеется бесконечное множество полиномиальных сохраняющихся плотностей.
Впрочем позже оказалось, что данная теорема возможно доказана с пробелами [2, стр. 159]
и тока
задаются формулами
требование гладкости (
) [5, стр. 441]
Многосолитонные решения
В линейных уравнений всё проще: взаимодействий между решениями нет, они обладают свойством суперпозиции, что означает, если и
являются решением линейного уравнения, то и их сумма
также будет решением, то есть удовлетворять линейному уравнению. Это следует из того, что производная любого порядка, в том числе смешанная) от суммы равна сумме производных, и тоже самое с линейными функциями от
, поэтому при постановке суммы решений в уравнение оно остается верным.
— скорость соответствующего солитона,
— его положение в момент времени
,
знаками задают тип столкновения (кинк-антикинк) по некоторому соотношению.

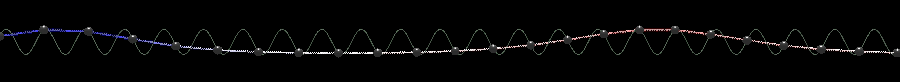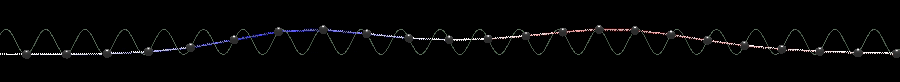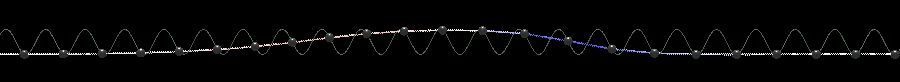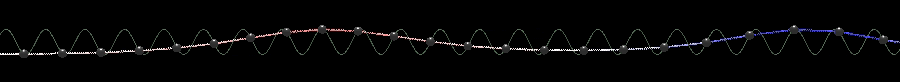

Солитонный атом
) решение типа «бризер» задается формулой [4, стр. 50]
отвечающим за частоту осцилляции.

задается формулой [5, стр. 440]:
.
Обнаружение других солитонных уравнений
, инвариантны, коль скоро функция
меняется согласно КдФ-уравнению. То есть собственные значения являются интегралами уравнения КдФ. [2, стр. 41], [24]
Заключение
Литература
Список


