Преобразуем изображение в звук — что можно услышать?

Привет Хабр.

В недавней публикации здесь на сайте описывалось устройство, позволяющее незрячим людям «видеть» изображение, преобразуя его с помощью звуковых волн. С технической точки зрения, в той статье не было никаких деталей вообще (а вдруг украдут идею за миллион), но сама концепция показалась интересной. Имея некоторый опыт обработки сигналов, я решил поэкспериментировать самостоятельно.

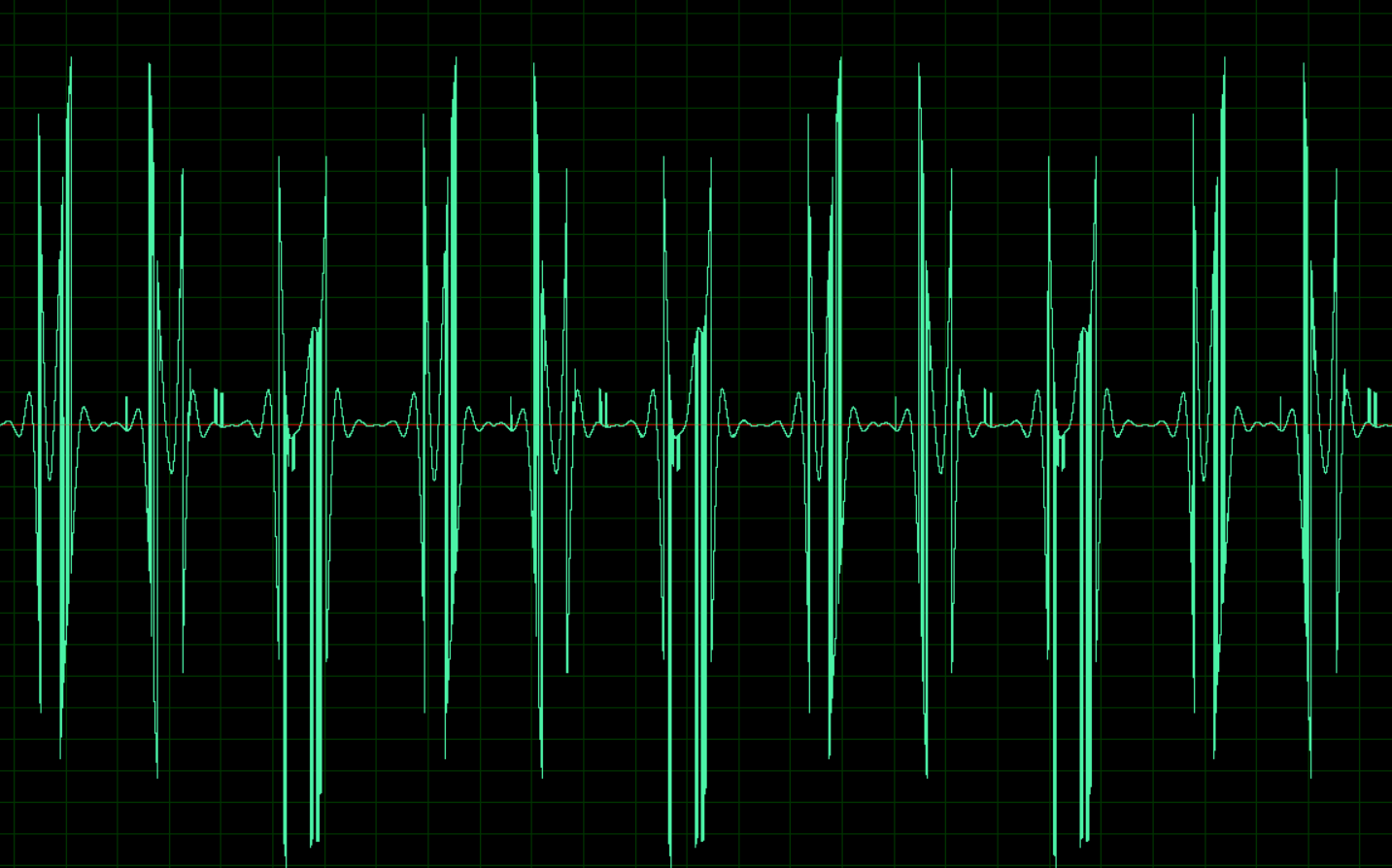
Что из этого получилось, подробности и примеры файлов под катом.

Преобразуем 2D в 1D

Первая очевидная задача, которая нас ожидает — это преобразовать двухмерное «плоское» изображение в «одномерную» звуковую волну. Как подсказали в комментариях к той статье, для этого удобно воспользоваться кривой Гильберта.

Она по своей сути похожа на фрактал, и идея в том, что при увеличении разрешения изображения, относительное расположение объектов не меняется (если объект был в верхнем левом углу картинки, то он останется там же). Различные размерности кривых Гильберта могут дать нам разные изображения: 32×32 для N=5, 64×64 для N=6, и так далее. «Обходя» изображение по этой кривой, мы получаем линию, одномерный объект.

Следующий вопрос это размер картинки. Интуитивно хочется взять изображение побольше, но тут есть большое «но»: даже картинка 512х512, это 262144 точек. Если преобразовать каждую точку в звуковой импульс, то при частоте дискретизации 44100, мы получим последовательность длиной в целых 6 секунд, а это слишком долго — изображения должны обновляться быстро, например с использованием web-камеры. Делать частоту дискретизации выше бесмысленно, мы получим ультразвуковые частоты, неслышимые ухом (хотя для совы или летучей мыши может и пойдет). В итоге методом научного тыка было выбрано разрешение 128х128, которое даст импульсы длиной 0.37c — с одной стороны, это достаточно быстро чтобы ориентироваться в реальном времени, с другой вполне достаточно, чтобы уловить на слух какие-то изменения в форме сигнала.

Обработка изображения

Первым шагом мы загружаем изображение, преобразуем его в ч/б и масштабируем до нужного размера. Размер изображения зависит от размерности кривой Гильберта.

from PIL import Image from hilbertcurve.hilbertcurve import HilbertCurve import numpy as np from scipy.signal import butter, filtfilt   # Create Hilbert curve dimension = 7 hilbert = HilbertCurve(dimension, n=2) print("Hilbert curve dimension:", dimension)  # Maximum distance along curve print("Max_dist:", hilbert.max_h)  # Maximum distance along curve print("Max_coord:", hilbert.max_x)  # Maximum coordinate value in any dimension  # Load PIL image f_name = "image01.png" img = Image.open(f_name) width, height = img.size out_size = hilbert_curve.max_x + 1 if width != out_size:     img = img.resize((out_size, out_size), Image.ANTIALIAS)  # Get image as grayscale numpy array img_grayscale = img.convert(mode='L') img_data = np.array(img_grayscale)

Следующим шагом формируем звуковую волну. Тут разумеется, может быть великое множество алгоритмов и ноухау, для теста я просто взял яркостную составляющую. Разумеется, наверняка есть способы лучше.

width, height = img_grayscale.size  sound_data = np.zeros(width*height) for ii in range(width*height):     coord_x, coord_y = hilbert_curve.coordinates_from_distance(ii)     pixel_l = img_data[coord_x][coord_y]      # Inverse colors (paper-like, white = 0, black = 255)     pixel_l = 255 - pixel_l      # 0..255 => 0..32768     ampl = pixel_l*32      sound_data[ii] = ampl

Из кода, надеюсь, все понятно. Функция coordinates_from_distance делает за нас всю работу по преобразованию координат (х, у) в расстояние на кривой Гильберта, значение яркости L мы инвертируем и преобразуем в цвет.

Это еще не все. Т.к. на изображении могут быть большие блоки одного цвета, это может привести к появлению в звуке «dc-компоненты» — длинного ряда отличных от нуля значений, например [100,100,100,…]. Чтобы их убрать, применим к нашему массиву high-pass filter (фильтр Баттерворта) с частотой среза 50Гц (совпадение с частотой сети случайно). Синтез фильтров есть в библиотеке scipy, которым мы и воспользуемся.

def butter_highpass(cutoff, fs, order=5):     nyq = 0.5 * fs     normal_cutoff = cutoff / nyq     b, a = butter(order, normal_cutoff, btype='high', analog=False)     return b, a  def butter_highpass_filter(data, cutoff, fs, order=5):     b, a = butter_highpass(cutoff, fs, order)     y = filtfilt(b, a, data)     return y  # Apply high pass filter to remove dc component  cutoff_hz = 50 sample_rate = 44100 order = 5 wav_data = butter_highpass_filter(sound_data, cutoff_hz, sample_rate, order)

Последним шагом сохраним изображение. Т.к. длина одного импульса короткая, мы повторяем его 10 раз, это будет на слух более приближено к реальному повторяющемуся изображению, например с веб-камеры.

# Clip data to int16 range sound_output = np.clip(wav_data, -32000, 32000).astype(np.int16)  # Save repeat = 10 sound_output_ntimes = np.tile(sound_output, repeat) wav_name = "ouput.wav" scipy.io.wavfile.write(wav_name, sample_rate, sound_output_ntimes)

Результаты

Вышеприведенный алгоритм, разумеется, совсем примитивный. Я хотел проверить три момента — насколько можно различать разные несложные фигуры, и насколько можно оценить расстояние до фигур.

Тест-1

Изображению соответствует такой звуковой сигнал: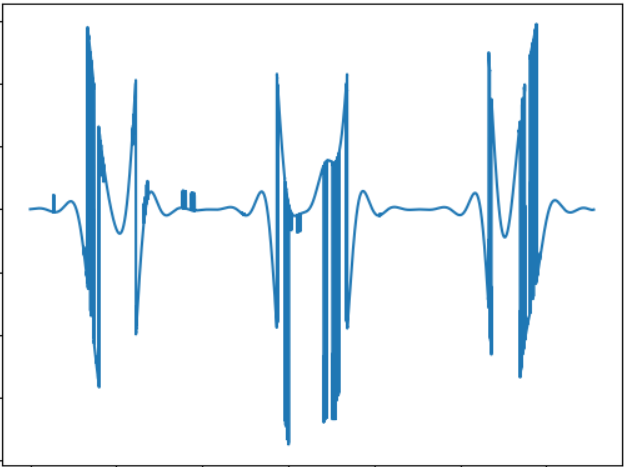

WAV: cloud.mail.ru/public/nt2R/2kwBvyRup

Тест-2

Идея этого теста — сравнить «звучание» объекта другой формы. Звуковой сигнал: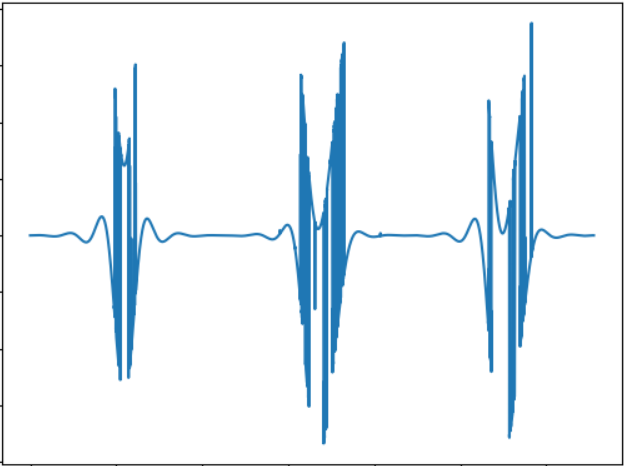

WAV: cloud.mail.ru/public/2rLu/4fCNRxCG2

Можно заметить, что звучание действительно другое, и на слух разница есть.

Тест-3

Идея теста — проверить объект меньшего размера. Звуковой сигнал: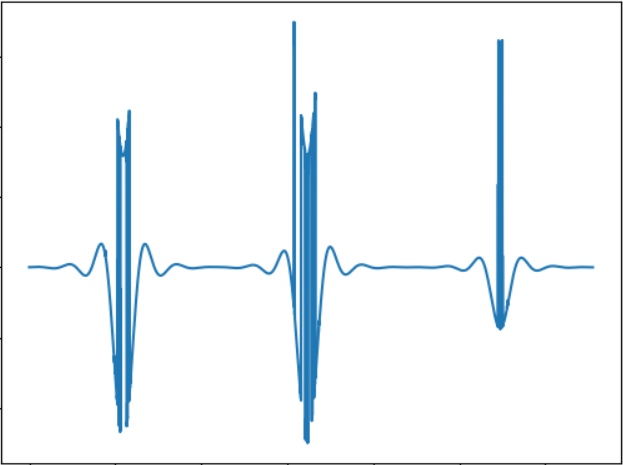

WAV: cloud.mail.ru/public/5GLV/2HoCHvoaY

В принципе, чем меньше размеры объекта, тем меньше будет «всплесков» в звуке, так что зависимость тут вполне прямая.

Заключение

Данный тест, разумеется, не диссертация, а просто proof of concept, сделанный за несколько часов свободного времени. Но даже так, оно в принципе работает, и разницу ощущать на слух вполне реально. Я не знаю, можно ли научиться ориентироваться в пространстве по таким звукам, гипотетически наверно можно. Хотя тут огромное поле для улучшений и экспериментов, например, можно использовать стереозвук, что позволит лучше разделять объекты с разных сторон, можно экспериментировать с другими способами конвертации изображения в звук, например, кодировать цвет разными частотами, и пр. И наконец, перспективным тут является использование 3d-камер, способных воспринимать глубину (увы, такой камеры в наличии нет). Кстати, с помощью несложного кода на OpenCV, вышеприведенный алгоритм можно адаптировать к использованию web-камеры, что позволит экспериментировать с динамическими изображениями.

Ну и как обычно, всем удачных экспериментов.