Часть 1: Млечный путь
В предыдущем посте я рассказывал, как в «Ведьмаке 3» реализованы падающие звёзды. Этого эффекта нет в «Крови и вине». В посте я опишу эффект, который есть только в этом DLC: Млечный путь.
Вот видео, в котором показан Млечный путь.
И несколько скриншотов: (1) до вызова отрисовки купола неба, (2) только с цветом Млечного пути, (3) после вызова:



Готовый кадр только с одним Млечным путём (без цвета неба и звёзд) выглядит так:

Эффект Млечного пути, ставший одним из самых сильных отличий от версии игры 2015 года, вкратце упомянут в разделе «Глупые трюки с небом». Давайте разберёмся, как он реализован!
План изложения будет привычным: сначала мы вкратце объясним всё, относящееся к геометрии, а затем расскажем про пиксельный шейдер.
1. Геометрия
Давайте начнём с используемого меша купола неба. Есть два серьёзных отличия между куполом 2015 года (основная игра + DLC «Каменные сердца», я обычно называю их обе «игрой 2015 года») и куполом в DLC «Кровь и вино» (2016 год):
а) В «Крови и вине» меш намного более плотный,
б) В меше купола неба «КиВ» используются векторы нормалей.
Вот меш купола неба 2015 года — DrawIndexed(720)
Меш купола неба в «Ведьмаке 3» 2015 года — 720 индексов
А вот меш из «КиВ» — DrawIndexed(2640):
Меш купола неба DLC «Ведьмак 3: Кровь и вино» — 2640 индексов
Вот ещё раз меш из «КиВ»: я нарисовал, как распределены нормали — они направлены в «центр» меша.
Меш купола неба DLC «Кровь и вино» с нормалями
2. Вершинный шейдер
Вершинный шейдер купола неба довольно прост. Вот соответствующий ассемблерный код. Ради простоты я пропустил вычисление SV_Position:
vs_5_0
dcl_globalFlags refactoringAllowed
dcl_constantbuffer cb1[4], immediateIndexed
dcl_constantbuffer cb2[6], immediateIndexed
dcl_input v0.xyz
dcl_input v1.xy
dcl_input v2.xyz
dcl_output o0.xyzw
dcl_output o1.xyzw
dcl_output_siv o2.xyzw, position
dcl_temps 3
0: mov o0.xy, v1.xyxx
1: mad r0.xyz, v0.xyzx, cb2[4].xyzx, cb2[5].xyzx
2: mov r0.w, l(1.000000)
3: dp4 o0.z, r0.xyzw, cb2[0].xyzw
4: dp4 o0.w, r0.xyzw, cb2[1].xyzw
5: mad r1.xyz, v2.xyzx, l(2.000000, 2.000000, 2.000000, 0.000000), l(-1.000000, -1.000000, -1.000000, 0.000000)
6: dp3 r2.x, r1.xyzx, cb2[0].xyzx
7: dp3 r2.y, r1.xyzx, cb2[1].xyzx
8: dp3 r2.z, r1.xyzx, cb2[2].xyzx
9: dp3 r1.x, r2.xyzx, r2.xyzx
10: rsq r1.x, r1.x
11: mul o1.xyz, r1.xxxx, r2.xyzx
12: dp4 o1.w, r0.xyzw, cb2[2].xyzw Входными данными из буфера вершин являются:
1) Позиция в локальном пространстве [0-1] — v0.xyz,
2) Texcoords — v1.xy,
3) Вектор нормали [0-1] — v2.xyz
Входящие данные из cbuffer:
1) Матрица мира (0-3) — классический подход: однородное масштабирование и преобразование по позиции камеры,
2) Масштаб и смещение для вершины (4-5) — трюк, используемый в течении игры для преобразования из локального пространства [0-1] в пространство [-1;1], и для потенциального «сплющивания» мешей.
А вот краткое описание того, что происходит в шейдере:
Шейдер начинается с простой передачи texcoords (строка 0). К позиции вершины в мире применяется масштаб и смещение (строка 1), а результат умножается на матрицу мира (строки 3-4, 12). Вектор нормали должен быть перенесён из интервала [0-1] в [-1;1] (строка 5), а затем он умножается на матрицу мира (строки 6-8) и в конце нормализуется (строки 9-11).
Готовые выходные данные имеют следующую схему:
3. Пиксельный шейдер
Вычисления Млечного пути — это просто одна часть шейдера неба. В «КиВ» он гораздо длиннее, чем в версии 2015 года. Он состоит из 385 строк на ассемблере, а вариант 2015 года — из 267 строк.
Давайте рассмотрим фрагмент ассемблерного кода, отвечающий за Млечный путь:
175: sample_indexable(texturecube)(float,float,float,float) r4.xyz, r2.xyzx, t0.xyzw, s0
176: mul r4.xyz, r4.xyzx, r4.xyzx
177: sample_indexable(texturecube)(float,float,float,float) r0.w, r2.xyzx, t1.yzwx, s0
178: dp3 r1.w, v1.xyzx, v1.xyzx
179: rsq r1.w, r1.w
180: mul r2.xyz, r1.wwww, v1.xyzx
181: dp3 r1.w, cb12[204].yzwy, cb12[204].yzwy
182: rsq r1.w, r1.w
183: mul r5.xyz, r1.wwww, cb12[204].yzwy
184: dp3 r1.w, r2.xyzx, r5.xyzx
185: mad_sat r0.w, r0.w, l(0.200000), r1.w
186: ge r1.w, l(0.497925), r0.w
187: if_nz r1.w
188: ge r1.w, l(0.184939), r0.w
189: mul r2.y, r0.w, l(5.407188)
190: min r2.z, r2.y, l(1.000000)
191: mad r2.w, r2.z, l(-2.000000), l(3.000000)
192: mul r2.z, r2.z, r2.z
193: mul r2.z, r2.z, r2.w
194: mul r5.xyz, r2.zzzz, l(0.949254, 0.949254, 0.949254, 0.000000)
195: mov r2.x, l(0.949254)
196: movc r2.xw, r1.wwww, r2.xxxy, l(0.000000, 0.000000, 0.000000, 0.500000)
197: not r4.w, r1.w
198: if_z r1.w
199: ge r1.w, l(0.239752), r0.w
200: add r5.w, r0.w, l(-0.184939)
201: mul r6.y, r5.w, l(18.243849)
202: mov_sat r5.w, r6.y
203: mad r6.z, r5.w, l(-2.000000), l(3.000000)
204: mul r5.w, r5.w, r5.w
205: mul r5.w, r5.w, r6.z
206: mad r5.w, r5.w, l(-0.113726), l(0.949254)
207: movc r5.xyz, r1.wwww, r5.wwww, r5.zzzz
208: and r7.xyz, r1.wwww, l(0.949254, 0.949254, 0.949254, 0.000000)
209: mov r6.x, l(0.835528)
210: movc r2.xw, r1.wwww, r6.xxxy, r2.xxxw
211: mov r2.xyzw, r2.xxxw
212: else
213: mov r7.xyz, l(0, 0, 0, 0)
214: mov r2.xyzw, r2.xxxw
215: mov r1.w, l(-1)
216: endif
217: not r5.w, r1.w
218: and r4.w, r4.w, r5.w
219: if_nz r4.w
220: ge r5.w, r0.w, l(0.239752)
221: ge r6.x, l(0.294564), r0.w
222: and r1.w, r5.w, r6.x
223: add r5.w, r0.w, l(-0.239752)
224: mul r6.w, r5.w, l(18.244175)
225: mov_sat r5.w, r6.w
226: mad r7.w, r5.w, l(-2.000000), l(3.000000)
227: mul r5.w, r5.w, r5.w
228: mul r5.w, r5.w, r7.w
229: mad r5.w, r5.w, l(0.015873), l(0.835528)
230: movc r5.xyz, r1.wwww, r5.wwww, r5.xyzx
231: movc r7.xyz, r1.wwww, l(0.835528, 0.835528, 0.835528, 0.000000), r7.xyzx
232: mov r6.xyz, l(0.851401, 0.851401, 0.851401, 0.000000)
233: movc r2.xyzw, r1.wwww, r6.xyzw, r2.xyzw
234: endif
235: not r5.w, r1.w
236: and r4.w, r4.w, r5.w
237: if_nz r4.w
238: ge r1.w, r0.w, l(0.294564)
239: add r0.w, r0.w, l(-0.294564)
240: mul r6.w, r0.w, l(4.917364)
241: mov_sat r0.w, r6.w
242: mad r4.w, r0.w, l(-2.000000), l(3.000000)
243: mul r0.w, r0.w, r0.w
244: mul r0.w, r0.w, r4.w
245: mad r0.w, r0.w, l(-0.851401), l(0.851401)
246: movc r5.xyz, r1.wwww, r0.wwww, r5.xyzx
247: movc r7.xyz, r1.wwww, l(0.851401, 0.851401, 0.851401, 0.000000), r7.xyzx
248: mov r6.xyz, l(0, 0, 0, 0)
249: movc r2.xyzw, r1.wwww, r6.xyzw, r2.xyzw
250: endif
251: else
252: mov r7.xyz, l(0, 0, 0, 0)
253: mov r2.xyzw, l(0.000000, 0.000000, 0.000000, 0.500000)
254: mov r1.w, l(0)
255: endif
256: mov_sat r2.w, r2.w
257: mad r0.w, r2.w, l(-2.000000), l(3.000000)
258: mul r2.w, r2.w, r2.w
259: mul r0.w, r0.w, r2.w
260: add r2.xyz, -r7.xyzx, r2.xyzx
261: mad r2.xyz, r0.wwww, r2.xyzx, r7.xyzx
262: movc r2.xyz, r1.wwww, r5.xyzx, r2.xyzx
263: mul r2.xyz, r2.xyzx, l(0.150000, 0.200000, 0.250000, 0.000000)Довольно пугающе, не так ли? Когда я увидел его впервые (это было до того, как я увидел шейдер падающих звёзд), то подумал: «Что это за ад? Этот код невозможно реверсировать!»
Но есть один аспект — если вы читали пост про падающие звёзды, то можете легко узнать этот паттерн. Код работает очень похоже на отрисовку метеоритов! Скоро мы поговорим и о кривой.
Фрагмент начинается с сэмплирования кубической карты звёзд (строка 175), где направление сэмплирования хранится в r2.xyz. Как видите, в строке line 177 есть инструкция сэмплировпния ещё одной кубической карты. В отличие от шейдера 2015 года, в шейдере «КиВ» есть ещё одна текстура «кубическая карта шума», грани которой выглядят примерно так:
Прежде чем мы доберёмся до кривой, давайте найдём входящие данные для неё. Сначала вычисляется скалярное произведение (строка 184) между нормализованным вектором нормали купола неба (строки 178-180) и вектором света Луны (строки 181-183) — по сути, это N*L.
Вот визуализация скалярного произведения (в линейном пространстве):

Значение, используемое в качестве входящих данных для функции «кривой Млечного пути», получается в строке 185:
x = saturate( noise * 0.2 + Ndot );
А вот визуализация такого искажённого N*L, тоже в линейном пространстве:

Теперь давайте перейдём к функции Млечного пути! Она чуть сложнее, чем функция падающих звёзд. Как я говорил в предыдущем посте, мы начинаем со списка контрольных точек по оси x. Взглянув на ассемблерный код, мы сразу их увидим:
// Control points (x-axis)
float controlPoint0 = 0.0;
float controlPoint1 = 0.184939;
float controlPoint2 = 0.239752;
float controlPoint3 = 0.294564;
float controlPoint4 = 0.497925; Откуда мы знаем, что первые контрольные точки равны нулю? Это довольно просто: в строке 189 нет инструкции «add».
Согласно посту о падающих звёздах, контрольные точки определяют количество сегментов, а далее нам нужно найти для них веса.
Для первого сегмента это довольно просто. Вес равен 0.949254:
194: mul r5.xyz, r2.zzzz, l(0.949254, 0.949254, 0.949254, 0.000000)
195: mov r2.x, l(0.949254) Давайте попробуем найти их для второго и третьего сегментов:
206: mad r5.w, r5.w, l(-0.113726), l(0.949254)
207: movc r5.xyz, r1.wwww, r5.wwww, r5.zzzz
208: and r7.xyz, r1.wwww, l(0.949254, 0.949254, 0.949254, 0.000000)
209: mov r6.x, l(0.835528)
...
229: mad r5.w, r5.w, l(0.015873), l(0.835528)
230: movc r5.xyz, r1.wwww, r5.wwww, r5.xyzx
231: movc r7.xyz, r1.wwww, l(0.835528, 0.835528, 0.835528, 0.000000), r7.xyzx
232: mov r6.xyz, l(0.851401, 0.851401, 0.851401, 0.000000) Именно на этом моменте я прекратил писать статью, потому что здесь что-то было не так (один из моментов, когда ты думаешь «хмм»). Посмотрите, всё не так легко, как простое умножение на один вес. Кроме того, откуда взялись значения наподобие -0.113726 и 0.015873?
Потом я понял, что эти значения просто являются разностями между максимальными возможными значениями в каждом сегменте ( 0.835528 — 0.949254 = -0.113726 и 0.851401 — 0.835528 = 0.015873)! Довольно очевидно (один из моментов, когда ты думаешь «эврика!»). Как оказалось, эти значения являются не весами, а просто координатами y точек, образующих кривую!
Это многое меняет и упрощает. Во-первых, мы можем избавиться от веса в функции, которую использовали в предыдущем посте
float getSmoothTransition(float cpLeft, float cpRight, float x)
{
return smoothstep( 0, 1, linstep(cpLeft, cpRight, x) );
} И можем записать функцию Млечного пути следующим образом:
float milkyway_curve( float x )
{
// Define a set of 2D points which form the curve
// Of course, you can use a Point2D-like struct here
// Control points (x-axis)
float controlPoint0 = 0.0;
float controlPoint1 = 0.184939;
float controlPoint2 = 0.239752;
float controlPoint3 = 0.294564;
float controlPoint4 = 0.497925;
// Values at points (y-axis)
float value0 = 0.0;
float value1 = 0.949254;
float value2 = 0.835528;
float value3 = 0.851401;
float value4 = 0.0;
float function_value = 0.0;
[branch] if (x <= controlPoint4)
{
[branch] if (x <= controlPoint1)
{
float t = getSmoothTransition(controlPoint0, controlPoint1, x);
function_value = lerp(value0, value1, t);
}
[branch] if (x >= controlPoint1 && x <= controlPoint2)
{
float t = getSmoothTransition(controlPoint1, controlPoint2, x);
function_value = lerp(value1, value2, t);
}
[branch] if (x >= controlPoint2 && x <= controlPoint3)
{
float t = getSmoothTransition(controlPoint2, controlPoint3, x);
function_value = lerp(value2, value3, t);
}
[branch] if (x >= controlPoint3)
{
float t = getSmoothTransition(controlPoint3, controlPoint4, x);
function_value = lerp(value3, value4, t);
}
}
return function_value;
} Это обобщённое решение для любого количества точек, образующих плавную кривую. Кроме того, оно объясняет происхождение «странных» значений контрольных точек — вероятно, разработчики для задания точек использовали какой-то визуальный редактор.
Разумеется, тот же принцип применим к коду падающих звёзд.
Вот график функции:
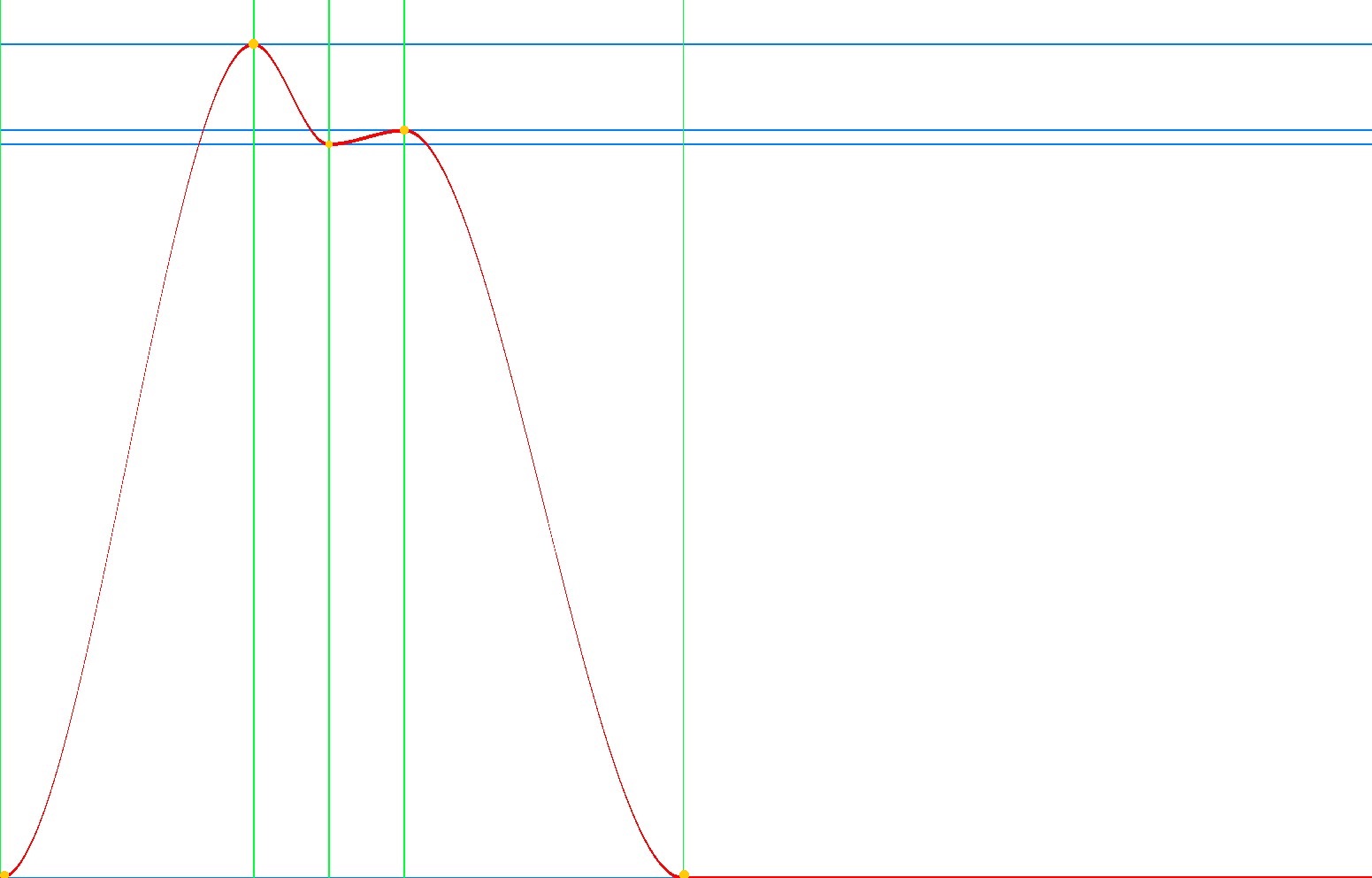
График функции Млечного пути.
Красное — значение функции,
Зелёное — координаты по x
Синее — координаты по y
Жёлтые точки — контрольные
Хорошо, но что дальше? В строке 263 мы умножаем значение из функции на синеватый цвет:
263: mul r2.xyz, r2.xyzx, l(0.150000, 0.200000, 0.250000, 0.000000) Но это ещё не конец! Нам просто нужно выполнить гамма-коррекцию:
263: mul r2.xyz, r2.xyzx, l(0.150000, 0.200000, 0.250000, 0.000000)
264: mad r2.xyz, r4.xyzx, l(3.000000, 3.000000, 3.000000, 0.000000), r2.xyzx
...
269: log r2.xyz, r2.xyzx
270: mul r2.xyz, r2.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
271: exp r2.xyz, r2.xyzx Теперь интересная штука: я назначил разные цвета контрольным точкам по оси x:
float3 gradient0 = float3(1, 0, 0);
float3 gradient1 = float3(0, 1, 0);
float3 gradient2 = float3(0, 0, 1);
float3 gradient3 = float3(1, 1, 0);
float3 gradient4 = float3(0, 1, 1); И вот что у меня получилось:

И на этом практически всё для Млечного пути сделано.
В строке 264 есть r4.xyz и…
4. Звёзды Туссента (бонус)
Я знаю, что эта часть статьи называется «Млечный путь», но не смог удержаться от того, чтобы не рассказать вкратце, как создаются звёзды Туссента. Они гораздо ярче, чем в Новиграде, на Скеллиге или в Велене.
В одном из предыдущих постов я рассказывал о звёздах 2015 года; настало время поговорить о звёздах 2016 года!
На самом деле, основная часть ассемблерного кода выглядит так:
175: sample_indexable(texturecube)(float,float,float,float) r4.xyz, r2.xyzx, t0.xyzw, s0
176: mul r4.xyz, r4.xyzx, r4.xyzx
...
264: mad r2.xyz, r4.xyzx, l(3.000000, 3.000000, 3.000000, 0.000000), r2.xyzx
...
269: log r2.xyz, r2.xyzx
270: mul r2.xyz, r2.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
271: exp r2.xyz, r2.xyzx
...
302: add r0.z, -cb0[9].w, l(1.000000)
303: mul r2.xyz, r0.zzzz, r2.xyzx
304: add r2.xyz, r2.xyzx, r2.xyzxНа HLSL это можно записать так:
float3 stars = texStars.Sample(sampler, starsDir).rgb;
stars *= stars;
float3 milkyway = milkyway_func(noisePerturbed) * float3(0.15, 0.20, 0.25);
float3 skyContribution = milkyway + 3.0 * stars;
// gamma correction
skyContribution = pow(skyContribution, 2.2);
// starsOpacity - 0.0 during the day (so stars and the Milky Way are not visible then), 1.0 during the night
float starsOpacity = 1.0 - cb0_v9.w;
skyContribution *= starsOpacity;
skyContribution *= 2;То есть сами звёзды просто умножаются на 3 (строка 264), а затем вместе с влиянием Млечного пути на 2 (строка 304) — олдскульный способ, но работает отлично!
Разумеется, позже происходит и кое-что ещё (например, мерцание звёзд при помощи целочисленного шума, и т.д.), но это уже не относится к теме статьи.
Заключение
В этой части я разобрался, как в «Ведьмаке 3: Кровь и вино» реализованы Млечный путь и звёзды.
Давайте заменим исходный шейдер кодом, который только написали. Готовый кадр выглядит вот так:

а с исходным шейдером кадр выглядит вот так:

Неплохо.
Часть 2: цветокоррекция
Один из эффектов постобработки, который можно встретить в «Ведьмаке 3» почти везде — это цветокоррекция. Её принцип заключается в использовании текстуры таблицы поиска (LUT) для преобразования одного множества цветов в другое.
Обычно процесс выглядит так: есть нейтральная (выходной цвет = входящему цвету) таблица поиска, которая редактируется в инструментах наподобие Adobe Photoshop — усиливается её контрастность/яркость/насыщенность/оттенок и т.д., то есть все модификации и изменения, которые достаточно затратны при вычислении в реальном времени. Благодаря LUT-ам эти операции можно заменить менее затратным поиском в текстуре.
Существует как минимум три известных мне цветовых таблиц LUT: трёхмерные, «длинные» двухмерные и «квадратные» двухмерные.

Нейтральная «длинная» двухмерная LUT

Нейтральная «квадратная» двухмерная LUT
Прежде чем мы перейдём к реализации цветокоррекции в «Ведьмаке 3», вот несколько полезных ссылок по этой технике:
Хорошая реализация на OpenGL с онлайн-демо
Исследование графики Metal Gear Solid V (хорошая статья в целом, есть раздел о цветокоррекции) [перевод на Хабре]
Цветокоррекция при помощи текстур поиска (LUT)
Статья из книги «GPU Gems 2» — цветокоррекция при помощи трёхмерных текстур
Документация UE4 о создании и использовании цветовых LUT
Давайте взглянем на пример LUT, использованной примерно в начале игры White Orchard — бОльшая часть зелёных цветов заменена на жёлтые:
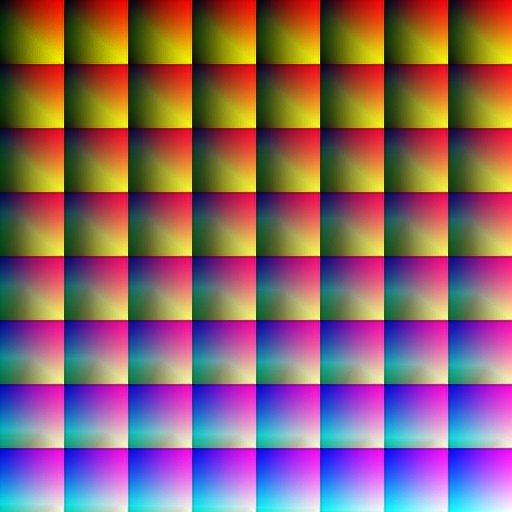
В «Ведьмаке 3» используются двухмерные текстуры размером 512×512.
В общем случае ожидается, что цветокоррекция будет выполняться в пространстве LDR. Поэтому получается 2563 возможных входящих значений — больше 16 миллионов комбинаций, преобразуемых всего в 5122=262 144 значения. Чтобы покрыть весь интервал входящих значений, используется билинейное сэмплирование.
А вот скриншоты для сравнения: до и после прохода цветокоррекции.


Как видите, разница невелика, но заметна — небо имеет более оранжевый оттенок.
Что касается реализации в «Ведьмаке 3», и входящий, и выходной render targets являются полноэкранными текстурами с плавающей запятой (R11G11B10). Любопытно, что конкретно в этой сцене каналы самых ярких пикселей (рядом с Солнцем) имеют значения, превышающие 1.0f — даже почти до 2.0f!
Вот ассемблерный код пиксельного шейдера:
ps_5_0
dcl_globalFlags refactoringAllowed
dcl_constantbuffer cb3[2], immediateIndexed
dcl_sampler s0, mode_default
dcl_sampler s1, mode_default
dcl_resource_texture2d (float,float,float,float) t0
dcl_resource_texture2d (float,float,float,float) t1
dcl_input_ps linear v1.xy
dcl_output o0.xyzw
dcl_temps 5
0: max r0.xy, v1.xyxx, cb3[0].xyxx
1: min r0.xy, r0.xyxx, cb3[0].zwzz
2: sample_indexable(texture2d)(float,float,float,float) r0.xyzw, r0.xyxx, t0.xyzw, s0
3: log r1.xyz, abs(r0.xyzx)
4: mul r1.xyz, r1.xyzx, l(0.454545, 0.454545, 0.454545, 0.000000)
5: exp r1.xyz, r1.xyzx
6: mad r2.xyz, r1.xyzx, l(1.000000, 1.000000, 0.996094, 0.000000), l(0.000000, 0.000000, 0.015625, 0.000000)
7: min r2.xyz, r2.xyzx, l(1.000000, 1.000000, 1.000000, 0.000000)
8: min r2.z, r2.z, l(0.999990)
9: add r2.xy, r2.xyxx, l(0.007813, 0.007813, 0.000000, 0.000000)
10: mul r2.xyzw, r2.xyzz, l(0.996094, 0.996094, 64.000000, 8.000000)
11: max r2.xy, r2.xyxx, l(0.015625, 0.015625, 0.000000, 0.000000)
12: min r2.xy, r2.xyxx, l(0.984375, 0.984375, 0.000000, 0.000000)
13: round_ni r3.xz, r2.wwww
14: mad r2.z, -r3.x, l(8.000000), r2.z
15: round_ni r3.y, r2.z
16: mul r2.zw, r3.yyyz, l(0.000000, 0.000000, 0.125000, 0.125000)
17: mad r2.xy, r2.xyxx, l(0.125000, 0.125000, 0.000000, 0.000000), r2.zwzz
18: sample_l(texture2d)(float,float,float,float) r2.xyz, r2.xyxx, t1.xyzw, s1, l(0)
19: mul r2.w, r1.z, l(63.750000)
20: round_ni r2.w, r2.w
21: mul r1.w, r2.w, l(0.015625)
22: mad r1.z, r1.z, l(63.750000), -r2.w
23: min r1.xyw, r1.xyxw, l(1.000000, 1.000000, 0.000000, 1.000000)
24: min r1.w, r1.w, l(0.999990)
25: add r1.xy, r1.xyxx, l(0.007813, 0.007813, 0.000000, 0.000000)
26: mul r1.xy, r1.xyxx, l(0.996094, 0.996094, 0.000000, 0.000000)
27: max r1.xy, r1.xyxx, l(0.015625, 0.015625, 0.000000, 0.000000)
28: min r1.xy, r1.xyxx, l(0.984375, 0.984375, 0.000000, 0.000000)
29: mul r3.xy, r1.wwww, l(64.000000, 8.000000, 0.000000, 0.000000)
30: round_ni r4.xz, r3.yyyy
31: mad r1.w, -r4.x, l(8.000000), r3.x
32: round_ni r4.y, r1.w
33: mul r3.xy, r4.yzyy, l(0.125000, 0.125000, 0.000000, 0.000000)
34: mad r1.xy, r1.xyxx, l(0.125000, 0.125000, 0.000000, 0.000000), r3.xyxx
35: sample_l(texture2d)(float,float,float,float) r1.xyw, r1.xyxx, t1.xywz, s1, l(0)
36: add r2.xyz, -r1.xywx, r2.xyzx
37: mad r1.xyz, r1.zzzz, r2.xyzx, r1.xywx
38: log r1.xyz, abs(r1.xyzx)
39: mul r1.xyz, r1.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
40: exp r1.xyz, r1.xyzx
41: mad r1.xyz, cb3[1].zzzz, r1.xyzx, -r0.xyzx
42: mad o0.xyz, cb3[1].yyyy, r1.xyzx, r0.xyzx
43: mov o0.w, r0.w
44: ret В целом, разработчики «Ведьмака 3» не стали изобретать велосипед и использую много «надёжного» кода. Это логично, ведь это один из эффектов, в котором нужно быть чрезвычайно аккуратным с координатами текстур.
Тем не менее, требуется два запроса к LUT, это следствие использования 2D-текстуры — необходимо симулировать билинейное сэмплирование канала синего. В представленной по ссылке выше реализации на OpenGL слияние этих двух запросов зависит от дробной части канала синего.
Что мне показалось интересным, так это отсутствие в ассемблерном коде инструкций ceil (round_pi) и frac (frc). Однако в нём довольно много инструкций floor (round_ni).
Шейдер начинается с получения входящей текстуры цвета и извлечения из неё цвета в гамма-пространстве:
float3 LinearToGamma(float3 c) { return pow(c, 1.0/2.2); }
float3 GammaToLinear(float3 c) { return pow(c, 2.2); }
...
// Set range of allowed texcoords
float2 minAllowedUV = cb3_v0.xy;
float2 maxAllowedUV = cb3_v0.zw;
float2 samplingUV = clamp( Input.Texcoords, minAllowedUV, maxAllowedUV );
// Get color in *linear* space
float4 inputColorLinear = texture0.Sample( samplerPointClamp, samplingUV );
// Calculate color in *gamma* space for RGB
float3 inputColorGamma = LinearToGamma( inputColorLinear.rgb ); Допустимые координаты сэмплирования min и max берутся из cbuffer:
Этот конкретный кадр был захвачен в разрешении 1920×1080 — значения max равны: (1919/1920, 1079/1080)
Довольно легко заметить, что ассемблерный код шейдера содержит два довольно похожих блока, за которыми следует получение данных из LUT. Поэтому я создал вспомогательную функцию, которая вычисляет uv для LUT. Давайте сначала взглянем на соответствующий ассемблерный код:
7: min r2.xyz, r2.xyzx, l(1.000000, 1.000000, 1.000000, 0.000000)
8: min r2.z, r2.z, l(0.999990)
9: add r2.xy, r2.xyxx, l(0.007813, 0.007813, 0.000000, 0.000000)
10: mul r2.xyzw, r2.xyzz, l(0.996094, 0.996094, 64.000000, 8.000000)
11: max r2.xy, r2.xyxx, l(0.015625, 0.015625, 0.000000, 0.000000)
12: min r2.xy, r2.xyxx, l(0.984375, 0.984375, 0.000000, 0.000000)
13: round_ni r3.xz, r2.wwww
14: mad r2.z, -r3.x, l(8.000000), r2.z
15: round_ni r3.y, r2.z
16: mul r2.zw, r3.yyyz, l(0.000000, 0.000000, 0.125000, 0.125000)
17: mad r2.xy, r2.xyxx, l(0.125000, 0.125000, 0.000000, 0.000000), r2.zwzz
18: sample_l(texture2d)(float,float,float,float) r2.xyz, r2.xyxx, t1.xyzw, s1, l(0) Здесь r2.xyz — это входящий цвет.
Первое, что происходит — проверка того, находятся ли входящие данные в интервале [0-1]. (строка 7). Это, например, используется для пикселей с компонентами > 1.0, как у вышеупомянутых пикселей Солнца.
Далее канал синего умножается на 0.99999 (строка 8), чтобы floor(color.b) возвращала значение в интервале [0-7].
Для вычисления координат LUT шейдер первым делом преобразует каналы красного и зелёного, чтобы «втиснуть» из в верхний левый сегмент. Канал синего [0-1] разрезается на 64 фрагмента, которые соответствуют всем 64 сегментам в текстуре поиска. На основании текущего значения канала синего выбирается соответствующий сегмент и вычисляется смещение для него.
Пример
Давайте, например, выберем (0.75, 0.5, 1.0). Каналы красного и зелёного преобразуются в верхний левый сегмент, что даёт нам:
float2 rgOffset = (0.75, 0.5) / 8 = (0.09375, 0.0625)
Далее мы проверяем, в каком из 64 сегментов расположено значение синего (1.0). Разумеется, в нашем случае это последний сегмент — 64.
Смещение выражается в сегментах (rowOffset, columnOffset):
float blue_rowOffset = 7.0;
float blue_columnOffset = 7.0;
float2 blueOffset =float2(blue_rowOffset, blue_columnOffset) / 8.0 = (0.875, 0.875)
В конце мы просто суммируем смещения:
float2 finalUV = rgOffset + blueOffset;
finalUV = (0.09375, 0.0625) + (0.875, 0.875) = (0.96875, 0.9375)
Это был просто короткий пример. Теперь давайте изучим подробности реализации.
Для каналов красного и зелёного (r2.xy) в строке 9 прибавляется смещение в полпикселя (0.5 / 64). Затем мы умножаем их на 0.996094 (строка 10) и ограничиваем их (clamp) особым интервалом (строки 11-12).
Необходимость смещения в полпикселя довольно очевидна — мы хотим выполнять сэмплирование из центра пикселя. Гораздо более загадочным аспектом является коэффициент масштабирования из строки 10 — он равен 63,75/64.0. Скоро мы расскажем о нём подробнее.
В конце координаты ограничиваются интервалом [1/64 — 63/64].
Зачем нам это нужно? Я не знаю точно, но похоже, это сделано для того, чтобы билинейное сэмплирование никогда не брало сэмплы за пределами сегмента.
Вот изображение с примером в виде сегмента 6×6, демонстрирующее, как работает эта операция ограничения (clamp):
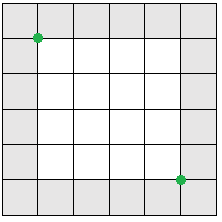
Вот сцена без применения clamp — заметьте довольно серьёзное обесцвечивание вокруг Солнца:

Для простоты сравнения покажу ещё раз результат из игры:

Вот фрагмент кода для этой части:
// * Calculate red/green offset
// half-pixel offset to always sample within centre of a pixel
const float halfOffset = 0.5 / 64.0;
const float scale = 63.75/64.0;
float2 rgOffset;
rgOffset = halfOffset + color.rg;
rgOffset *= scale;
rgOffset.xy = clamp(rgOffset.xy, float2(1.0/64.0, 1.0/64.0), float2(63.0/64.0, 63.0/64.0) );
// place within the top left slice
rgOffset.xy /= 8.0; Теперь пора найти смещение для канала синего.
Чтобы найти смещение строк канал синего делится на 8 частей, каждая из которых покрывает ровно одну строку в текстуре поиска.
// rows
bOffset.y = floor(color.b * 8); Чтобы найти смещение столбца, полученное значение нужно ещё раз разделить на 8 меньших частей, что соответствует всем 8 сегментам строки. Уравнение из шейдера довольно запутанное:
// columns
bOffset.x = floor(color.b * 64 - 8*bOffset.y ); На этом этапе стоит заметить, что:
frac(x) = x — floor(x)
Поэтому уравнение можно переписать так:
bOffset.x = floor(8 * frac(color.b * 8) ); А вот фрагмент кода для этого:
// * Calculate blue offset
float2 bOffset;
// rows
bOffset.y = floor(color.b * 8);
// columns
bOffset.x = floor(color.b * 64 - 8*bOffset.y );
// or:
// bOffset.x = floor(8 * frac(color.b * 8) );
// at this moment bOffset stores values in [0-7] range, we have to divide it by 8.0.
bOffset /= 8.0;
float2 lutPos = rgOffset + bOffset;
return lutPos; Таким образом мы получили функцию, возвращающую координаты текстуры для сэмплирования текстуры LUT. Давайте назовём эту функцию «getUV».
float2 getUV(in float3 color)
{
...
} Теперь вернёмся к основной функции шейдера. Как говорилось выше, из-за использования двухмерной LUT для симуляции билинейного сэмплирования канала синего нужны два запроса к LUT (из двух соседних друг с другом сегментов).
Рассмотрим следующий фрагмент на HLSL:
// Part 1
float scale_1 = 63.75/64.0;
float offset_1 = 1.0/64.0; // 0.015625
float3 inputColor1 = inputColorGamma;
inputColor1.b = inputColor1.b * scale_1 + offset_1;
float2 uv1 = getUV(inputColor1);
float3 color1 = texLUT.SampleLevel( sampler1, uv1, 0 ).rgb;
// Part 2
float3 inputColor2 = inputColorGamma;
inputColor2.b = floor(inputColorGamma.b * 63.75) / 64;
float2 uv2 = getUV(inputColor2);
float3 color2 = texLUT.SampleLevel( sampler1, uv2, 0 ).rgb;
// frac(x) = x - floor(x);
//float blueInterp = inputColorGamma.b*63.75 - floor(inputColorGamma.b * 63.75);
float blueInterp = frac(inputColorGamma.b * 63.75);
// Final LUT-corrected color
const float lutCorrectedMult = cb3_v1.z;
float3 finalLUT = lerp(color2, color1, blueInterp);
finalLUT = lutCorrectedMult * GammaToLinear(finalLUT);Принцип заключается в том, чтобы получать цвета из двух расположенных по соседству сегментов, а затем выполнять интерполяцию между ними — величина интерполяции зависит от дробной части входящего синего цвета.
Part 1 получает цвет из «дальнего» сегмента из-за явно заданного смещения синего ( + 1.0 / 64 );
Результат интерполяции хранится в переменной «finalLUT». Заметьте, что после этого результат снова возвращается в линейное пространство и умножается на lutCorrectedMult. В этом конкретном кадре его значение равно 1.00916. Это позволяет изменять яркость цвета LUT.
Очевидно, самой интригующей частью является «63.75» и «63.75 / 64». Я не совсем понимаю, откуда они берутся. Единственное объяснение, которое я нашёл: 63.75 / 64.0 = 510.0 / 512.0. Как говорилось выше существует ограничение (clamp) для каналов .rg, то есть при прибавлении смещения синего это по сути означает, что самые внешние строки и столбцы LUT не будут использоваться напрямую. Думаю, что цвета явным образом «втиснуты» в центр области текстуры поиска размером 510×510.
Давайте допустим, что inputColorGamma.b = 0.75 / 64.0.
Вот как это работает:
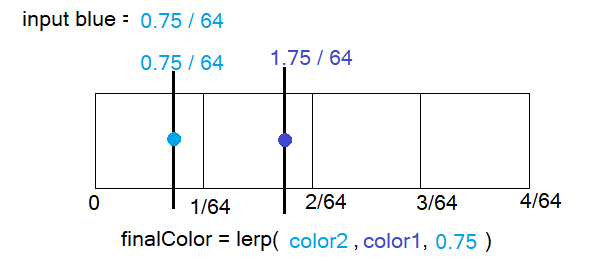
Здесь у нас есть первые четыре сегмента (1-4), которые покрывают канал синего с [0 — 4/64].
Судя по расположению пикселя, похоже, что каналы красного и зелёного примерно равны 0.75 и 0.5.
Мы дважды выполняем запрос к LUT — «Part 1» указывает на сегмент 2, а «Part 2» указывает на первый сегмент.
А интерполяция основана на дробной части цвета, которая равна 0.75.
То есть окончательный результат имеет 75% цвета из первого сегмента и 25% цвета из второго.
Мы почти закончили. Последним нужно сделать следующее:
// Calculate the final color
const float lutCorrectedInfluence = cb3_v1.y; // 0.20 in this frame
float3 finalColor = lerp(inputColorLinear.rgb, finalLUT, lutCorrectedInfluence);
return float4( finalColor, inputColorLinear.a ); Ха! В этом случае окончательный цвет состоит из 80% входящего цвета и 20% цвета LUT!
Давайте снова проведём краткое сравнение изображений: входящий цвет (то есть, по сути, с 0% цветокоррекции), окончательный кадр (20%) и полностью обработанное изображение (100% влияния цветокоррекции):

0% цветокоррекции

20% цветокоррекции (истинный шейдер)

100% цветокоррекции
Несколько LUT
В некоторых случаях «Ведьмак 3» использует несколько LUT.
Вот сцена, в которой используются два LUT:

До прохода цветокоррекции

После прохода цветокоррекции
Используемые LUT:

LUT 1 (texture1)
LUT 2 (texture2)
Давайте изучим ассемблерный фрагмент из этой версии шейдера:
18: sample_l(texture2d)(float,float,float,float) r3.xyz, r2.xyxx, t2.xyzw, s2, l(0)
19: sample_l(texture2d)(float,float,float,float) r2.xyz, r2.xyxx, t1.xyzw, s1, l(0)
...
36: sample_l(texture2d)(float,float,float,float) r4.xyz, r1.xyxx, t2.xyzw, s2, l(0)
37: sample_l(texture2d)(float,float,float,float) r1.xyw, r1.xyxx, t1.xywz, s1, l(0)
38: add r3.xyz, r3.xyzx, -r4.xyzx
39: mad r3.xyz, r1.zzzz, r3.xyzx, r4.xyzx
40: log r3.xyz, abs(r3.xyzx)
41: mul r3.xyz, r3.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
42: exp r3.xyz, r3.xyzx
43: add r2.xyz, -r1.xywx, r2.xyzx
44: mad r1.xyz, r1.zzzz, r2.xyzx, r1.xywx
45: log r1.xyz, abs(r1.xyzx)
46: mul r1.xyz, r1.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
47: exp r1.xyz, r1.xyzx
48: add r2.xyz, -r1.xyzx, r3.xyzx
49: mad r1.xyz, cb3[1].xxxx, r2.xyzx, r1.xyzx
50: mad r1.xyz, cb3[1].zzzz, r1.xyzx, -r0.xyzx
51: mad o0.xyz, cb3[1].yyyy, r1.xyzx, r0.xyzx
52: mov o0.w, r0.w
53: ret К счастью, тут всё довольно просто. В соответствии с ассемблерным кодом мы получаем:
// Part 1
// ...
float2 uv1 = getUV(inputColor1);
float3 lut2_color1 = texture2.SampleLevel( sampler2, uv1, 0 ).rgb;
float3 lut1_color1 = texture1.SampleLevel( sampler1, uv1, 0 ).rgb;
// Part 2
// ...
float2 uv2 = getUV(inputColor2);
float3 lut2_color2 = texture2.SampleLevel( sampler2, uv2, 0 ).rgb;
float3 lut1_color2 = texture1.SampleLevel( sampler1, uv2, 0 ).rgb;
float blueInterp = frac(inputColorGamma.b * 63.75);
float3 lut2_finalLUT = lerp(lut2_color2, lut2_color1, blueInterp);
lut2_finalLUT = GammaToLinear(lut2_finalLUT);
float3 lut1_finalLUT = lerp(lut1_color2, lut1_color1, blueInterp);
lut1_finalLUT = GammaToLinear(lut1_finalLUT);
const float lut_Interp = cb3_v1.x;
float3 finalLUT = lerp(lut1_finalLUT, lut2_finalLUT, lut_Interp);
const float lutCorrectedMult = cb3_v1.z;
finalLUT *= lutCorrectedMult;
// Calculate the final color
const float lutCorrectedInfluence = cb3_v1.y;
float3 finalColor = lerp(inputColorLinear.rgb, finalLUT, lutCorrectedInfluence);
return float4( finalColor, inputColorLinear.a );
} После получения двух цветов из LUT между ними выполняется интерполяция в lut_Interp. Всё остальное практически такое же, как в версии с одной LUT.
В этом случае единственной дополнительной переменной является lut_interp, сообщающая, как смешиваются две LUT.
Её значение в этом конкретном кадре примерно равно 0.96, то есть finalLUT содержит 96% цвета из LUT2 и 4% цвета из LUT1.
Однако это ещё не конец! Сцена, которую я изучал в части «Туман» использует три LUT!
Давайте взглянем!

До прохода цветокоррекции

После прохода цветокоррекции

LUT1 (texture1)
LUT2 (texture2)

LUT3 (texture3)
И снова ассемблерный фрагмент:
23: mad r2.yz, r2.yyzy, l(0.000000, 0.125000, 0.125000, 0.000000), r3.xxyx
24: sample_l(texture2d)(float,float,float,float) r3.xyz, r2.yzyy, t2.xyzw, s2, l(0)
...
34: mad r1.xy, r1.xyxx, l(0.125000, 0.125000, 0.000000, 0.000000), r1.zwzz
35: sample_l(texture2d)(float,float,float,float) r4.xyz, r1.xyxx, t2.xyzw, s2, l(0)
36: add r4.xyz, -r3.xyzx, r4.xyzx
37: mad r3.xyz, r2.xxxx, r4.xyzx, r3.xyzx
38: log r3.xyz, abs(r3.xyzx)
39: mul r3.xyz, r3.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
40: exp r3.xyz, r3.xyzx
41: sample_l(texture2d)(float,float,float,float) r4.xyz, r1.xyxx, t1.xyzw, s1, l(0)
42: sample_l(texture2d)(float,float,float,float) r1.xyz, r1.xyxx, t3.xyzw, s3, l(0)
43: sample_l(texture2d)(float,float,float,float) r5.xyz, r2.yzyy, t1.xyzw, s1, l(0)
44: sample_l(texture2d)(float,float,float,float) r2.yzw, r2.yzyy, t3.wxyz, s3, l(0)
45: add r4.xyz, r4.xyzx, -r5.xyzx
46: mad r4.xyz, r2.xxxx, r4.xyzx, r5.xyzx
47: log r4.xyz, abs(r4.xyzx)
48: mul r4.xyz, r4.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
49: exp r4.xyz, r4.xyzx
50: add r3.xyz, r3.xyzx, -r4.xyzx
51: mad r3.xyz, cb3[1].xxxx, r3.xyzx, r4.xyzx
52: mad r3.xyz, cb3[1].zzzz, r3.xyzx, -r0.xyzx
53: mad r3.xyz, cb3[1].yyyy, r3.xyzx, r0.xyzx
54: add r1.xyz, r1.xyzx, -r2.yzwy
55: mad r1.xyz, r2.xxxx, r1.xyzx, r2.yzwy
56: log r1.xyz, abs(r1.xyzx)
57: mul r1.xyz, r1.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
58: exp r1.xyz, r1.xyzx
59: mad r1.xyz, cb3[2].zzzz, r1.xyzx, -r0.xyzx
60: mad r0.xyz, cb3[2].yyyy, r1.xyzx, r0.xyzx
61: mov o0.w, r0.w
62: add r0.xyz, -r3.xyzx, r0.xyzx
63: mad o0.xyz, cb3[2].wwww, r0.xyzx, r3.xyzx
64: ret К сожалению, эта версия шейдера гораздо более запутанная, чем предыдущие две. Например, UV под названием «uv1» раньше встречались в ассемблерном коде перед «uv2» (сравните ассемблерный код шейдера всего с одной LUT). Но здесь всё не так — UV для «Part 1» вычисляются в строке 34, UV для «Part 2» — в строке 23.
Потратив гораздо больше ожидаемого времени на изучение того, что здесь происходит и недоумевая, почему Part2, похоже, поменялась местами с Part1, я написал фрагмент кода на HLSL для трёх LUT:
// Part 1
// ...
float2 uv1 = getUV(inputColor1);
float3 lut3_color1 = texture3.SampleLevel( sampler3, uv1, 0 ).rgb;
float3 lut2_color1 = texture2.SampleLevel( sampler2, uv1, 0 ).rgb;
float3 lut1_color1 = texture1.SampleLevel( sampler1, uv1, 0 ).rgb;
// Part 2
// ...
float2 uv2 = getUV(inputColor2);
float3 lut3_color2 = texture3.SampleLevel( sampler3, uv2, 0 ).rgb;
float3 lut2_color2 = texture2.SampleLevel( sampler2, uv2, 0 ).rgb;
float3 lut1_color2 = texture1.SampleLevel( sampler1, uv2, 0 ).rgb;
float blueInterp = frac(inputColorGamma.b * 63.75);
// At first compute linear color for LUT 2 [assembly lines 36-40]
float3 lut2_finalLUT = lerp(lut2_color2, lut2_color1, blueInterp);
lut2_finalLUT = GammaToLinear(lut2_finalLUT);
// Compute linear color for LUT 1 [assembly: 45-49]
float3 lut1_finalLUT = lerp(lut1_color2, lut1_color1, blueInterp);
lut1_finalLUT = GammaToLinear(lut1_finalLUT);
// Interpolate between LUT 1 and LUT 2 [assembly: 50-51]
const float lut12_Interp = cb3_v1.x;
float3 lut12_finalLUT = lerp(lut1_finalLUT, lut2_finalLUT, lut12_Interp);
// Multiply the LUT1-2 intermediate result with scale factor [assembly: 52]
const float lutCorrectedMult_LUT1_2 = cb3_v1.z;
lut12_finalLUT *= lutCorrectedMult;
// Mix LUT1-2 intermediate result with the scene color [assembly: 52-53]
const float lutCorrectedInfluence_12 = cb3_v1.y;
lut12_finalLUT = lerp(inputColorLinear.rgb, lut12_finalLUT, lutCorrectedInfluence_12);
// Compute linear color for LUT3 [assembly: 54-58]
float3 lut3_finalLUT = lerp(lut3_color2, lut3_color1, blueInterp);
lut3_finalLUT = GammaToLinear(lut3_finalLUT);
// Multiply the LUT3 intermediate result with the scale factor [assembly: 59]
const float lutCorrectedMult_LUT3 = cb3_v2.z;
lut3_finalLUT *= lutCorrectedMult_LUT3;
// Mix LUT3 intermediate result with the scene color [assembly: 59-60]
const float lutCorrectedInfluence3 = cb3_v2.y;
lut3_finalLUT = lerp(inputColorLinear.rgb, lut3_finalLUT, lutCorrectedInfluence3);
// The final mix between LUT1+2 and LUT3 influence [assembly: 62-63]
const float finalInfluence = cb3_v2.w;
float3 finalColor = lerp(lut12_finalLUT, lut3_finalLUT, finalInfluence);
return float4( finalColor, inputColorLinear.a );
} После завершения всех запросов текстур сначала интерполируются результаты LUT1 и LUT2, затем они умножаются на коэффициент масштабирования, а далее комбинируются с линейным цветом основной сцены. Давайте назовём результат lut12_finalLUT.
Затем примерно то же самое происходит для LUT3 — умножаем на ещё один коэффициент масштабирования и комбинируем с цветом основной сцены, что даёт нам lut3_finalLUT.
В конце оба промежуточных результата снова интерполируются.
Вот значения из cbuffer:
Часть 3: порталы

Если вы достаточно долго играли в «Ведьмака 3», то знаете, что Геральт — не большой любитель порталов. Давайте разберёмся, действительно ли они так страшны.
В игре есть два типа порталов:

Синий портал

Огненный портал
Я объясню, как создаётся огненный. В основном потому, что его код проще, чем у синего 🙂
Вот как огненный портал выглядит в игре:
Самая важная часть — это, разумеется, огонь, вращающийся по направлению к центру, но сам эффект состоит не только из видимой части. Подробнее об этом позже.
План этой части довольно стандартен: сначала геометрия, потом вершинные и пиксельные шейдеры. Будет довольно много скриншотов и видео.
С точки зрения рендеринга порталы отрисовываются в прямом проходе со включенным смешиванием — довольно распространённый в игре приём; подробнее см. в части о падающих звёздах.
Ну что, приступим.
1. Геометрия
Вот как выглядит меш портала:
Локальное пространство — вид спереди
Локальное пространство — вид сбоку
Меш напоминает рог Гавриила. Вершинный шейдер сжимает его по одной оси, вот тот же меш после сжатия в виде сбоку (в мировом пространстве):
Меш портала после вершинного шейдера (вид сбоку)
Кроме позиции у каждой вершины есть дополнительные данные: важны для нас следующие (на этом этапе я буду демонстрировать визуализации из RenderDoc, а позже расскажу о них подробнее):
Texcoords (float2):
Tangent (float3):
Color (float3):
Все эти данные будут использованы позднее, но на этом этапе у нас уже слишком много данных для файла .obj, поэтому экспорт этого меша может вызвать проблемы. Я экспортировал каждый канал как отдельный файл .csv, а затем загрузил все файлы .csv в моё приложение на C++ и сборка меша на основании этих собранных данных выполняется во время выполнения.
2. Вершинный шейдер
Вершинный шейдер не особо интересен, но давайте всё равно взглянем на соответствующий фрагмент:
vs_5_0
dcl_globalFlags refactoringAllowed
dcl_constantbuffer cb1[7], immediateIndexed
dcl_constantbuffer cb2[6], immediateIndexed
dcl_input v0.xyz
dcl_input v1.xy
dcl_input v3.xyz
dcl_input v4.xyzw
dcl_input v6.xyzw
dcl_input v7.xyzw
dcl_input v8.xyzw
dcl_output o0.xyz
dcl_output o1.xyzw
dcl_output o2.xyz
dcl_output o3.xyz
dcl_output_siv o4.xyzw, position
dcl_temps 3
0: mov o0.xy, v1.xyxx
1: mul r0.xyzw, v7.xyzw, cb1[6].yyyy
2: mad r0.xyzw, v6.xyzw, cb1[6].xxxx, r0.xyzw
3: mad r0.xyzw, v8.xyzw, cb1[6].zzzz, r0.xyzw
4: mad r0.xyzw, cb1[6].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r0.xyzw
5: mad r1.xyz, v0.xyzx, cb2[4].xyzx, cb2[5].xyzx
6: mov r1.w, l(1.000000)
7: dp4 o0.z, r1.xyzw, r0.xyzw
8: mov o1.xyzw, v4.xyzw
9: dp4 o2.x, r1.xyzw, v6.xyzw
10: dp4 o2.y, r1.xyzw, v7.xyzw
11: dp4 o2.z, r1.xyzw, v8.xyzw
12: mad r0.xyz, v3.xyzx, l(2.000000, 2.000000, 2.000000, 0.000000), l(-1.000000, -1.000000, -1.000000, 0.000000)
13: dp3 r2.x, r0.xyzx, v6.xyzx
14: dp3 r2.y, r0.xyzx, v7.xyzx
15: dp3 r2.z, r0.xyzx, v8.xyzx
16: dp3 r0.x, r2.xyzx, r2.xyzx
17: rsq r0.x, r0.x
18: mul o3.xyz, r0.xxxx, r2.xyzx Вершинный шейдер очень похож на прочие шейдеры, которые мы встречали ранее.
После краткого анализа и сравнения схемы входных данных я выяснил, что выходную struct можно записать так:
struct VS_OUTPUT
{
float3 TexcoordAndViewSpaceDepth : TEXCOORD0;
float3 Color : TEXCOORD1;
float3 WorldSpacePosition : TEXCOORD2;
float3 Tangent : TEXCOORD3;
float4 PositionH : SV_Position;
}; Я хотел продемонстрировать один аспект — как шейдер получает глубину в пространстве обзора (o0.z): это просто компонент .w переменной SV_Position.
На gamedev.net есть тема, в которой это объясняется чуть подробнее.
3. Пиксельный шейдер
Вот сцена примера непосредственно перед отрисовкой портала:

… и после отрисовки:

кроме того, в утилите просмотра текстур RenderDoc есть полезная опция оверлея «Clear Before Draw», при помощи которой мы со всей точностью можем увидеть отрисованный портал:

Первый интересный аспект заключается в том, что сам слой пламени отрисовывается только в центральной области меша.
Пиксельный шейдер состоит из 186 строк, для удобства я выложил его сюда. Как обычно, во время объяснения я буду приводить соответствующие фрагменты на ассемблере.
Также стоит заметить, что 100 из 186 строк относятся к вычислению тумана.
В начале на вход подаются 4 текстуры: огонь (t0), шум/дым (t1), цвет сцены (t6) и глубина сцены (t15):
Текстура огня
Текстура шума/дыма

Цвет сцены

Глубина сцены
Также есть отдельный буфер констант с 14 параметрами, которые управляют эффектом:
Входящие данные: позиция, tangent и texcoords — довольно понятные концепции, но давайте внимательнее приглядимся к каналу «Color». После нескольких экспериментов мне кажется, что это не цвет сам по себе, а три различные маски, которые шейдер использует, чтобы различать отдельные слои и понимать, где применять различные эффекты:
Color.r — маска теплового марева. Как понятно из названия, она используется для эффекта теплового искажения воздуха (подробнее о нём позже):

Color.g — внутренняя маска. В основном используется для эффекта огня.

Color.b — задняя маска. Используется для определения того, где находится «задняя» часть портала.

Я считаю, что в случае подобных эффектов лучше описать отдельные слои, а не анализировать ассемблерный код от начала до конца, как я делал раньше.
Итак, поехали:
3.1. Слой огня
Для начала давайте исследуем самую важную часть: слой огня. Вот видео с ним:
Основной принцип реализации такого эффекта заключается в использовании статичных texcoords из данных для каждой вершины и анимировании их при помощи переменной истекшего времени из буфера констант. Благодаря таким анимированным texcoords мы сэмплируем текстуру (в нашем случае огня) при помощи сэмплера искажения/повтора.
Интересно, что в этом конкретном эффекте сэмплируется только канал .r текстуры огня. Чтобы эффект был более правдоподобным, описанным выше способом получаются два слоя огня, которые затем комбинируются друг с другом.
Ну, давайте наконец посмотрим на код!
Начинаем мы с того, что делаем texcoords более динамичными, когда они достигают центра меша:
const float2 texcoords = Input.TextureUV;
const float uvSquash = cb4_v4.x; // 2.50
...
const float y_cutoff = 0.2;
const float y_offset = pow(texcoords.y - y_cutoff, uvSquash); А вот то же самое, но на ассемблере:
21: add r1.z, v0.y, l(-0.200000)
22: log r1.z, r1.z
23: mul r1.z, r1.z, cb4[4].x
24: exp r1.z, r1.z Затем шейдер получает texcoords для первого слоя огня и сэмплирует текстуру огня:
const float elapsedTimeSeconds = cb0_v0.x;
const float uvScaleGlobal1 = cb4_v2.x; // 1.00
const float uvScale1 = cb4_v3.x; // 0.15
...
// Sample fire1 - the first fire layer
float fire1; // r1.w
{
float2 fire1Uv;
fire1Uv.x = texcoords.x;
fire1Uv.y = uvScale1 * elapsedTimeSeconds + y_offset;
const float scaleGlobal = floor(uvScaleGlobal1); // 1.0
fire1Uv *= scaleGlobal;
fire1 = texFire.Sample(samplerLinearWrap, fire1Uv).x;
} Вот соответствующий фрагмент на ассемблере:
25: round_ni r1.w, cb4[2].x
26: mad r2.y, cb4[3].x, cb0[0].x, r1.z
27: mov r2.x, v0.x
28: mul r2.xy, r1.wwww, r2.xyxx
29: sample_indexable(texture2d)(float,float,float,float) r1.w, r2.xyxx, t0.yzwx, s0 Вот как выглядит первый слой при elapsedTimeSeconds = 50.0:

Чтобы показать, что же делает y_cutoff, продемонстрируем ту же сцену, но с y_cutoff = 0.5:

Таким образом мы получили первый слой. Далее шейдер получает второй:
const float uvScale2 = cb4_v6.x; // 0.06
const float uvScaleGlobal2 = cb4_v7.x; // 1.00
...
// Sample fire2 - the second fire layer
float fire2; // r1.z
{
float2 fire2Uv;
fire2Uv.x = texcoords.x - uvScale2 * elapsedTimeSeconds;
fire2Uv.y = uvScale2 * elapsedTimeSeconds + y_offset;
const float fire2_scale = floor(uvScaleGlobal2);
fire2Uv *= fire2_scale;
fire2 = texFire.Sample(samplerLinearWrap, fire2Uv).x;
} А вот соответствующий ассемблерный фрагмент:
144: mad r2.x, -cb0[0].x, cb4[6].x, v0.x
145: mad r2.y, cb0[0].x, cb4[6].x, r1.z
146: round_ni r1.z, cb4[7].x
147: mul r2.xy, r1.zzzz, r2.xyxx
148: sample_indexable(texture2d)(float,float,float,float) r1.z, r2.xyxx, t0.yzxw, s0 То есть, как вы видите, единственное отличие заключается в UV: теперь X тоже анимируется.
Второй слой выглядит так:

Получив два слоя внутреннего огня, мы можем их скомбинировать. Однако этот процесс чуть сложнее, чем обычное умножение, поскольку в нём участвует внутренняя маска:
const float innerMask = Input.Color.y;
const float portalInnerColorSqueeze = cb4_v8.x; // 3.00
const float portalInnerColorBoost = cb4_v9.x; // 188.00
...
// Calculate inner fire influence
float inner_influence; // r1.z
{
// innerMask and "-1.0" are used here to control where the inner part of a portal is.
inner_influence = fire1 * fire2 + innerMask;
inner_influence = saturate(inner_influence - 1.0);
// Exponentation to hide less luminous elements of inner portal
inner_influence = pow(inner_influence, portalInnerColorSqueeze);
// Boost the intensity
inner_influence *= portalInnerColorBoost;
} Вот соответствующий ассемблерный код:
149: mad r1.z, r1.w, r1.z, v1.y
150: add_sat r1.z, r1.z, l(-1.000000)
151: log r1.z, r1.z
152: mul r1.z, r1.z, cb4[8].x
153: exp r1.z, r1.z
154: mul r1.z, r1.z, cb4[9].x Получив inner_influence, которая является ни чем иным, как маской для внутреннего огня, мы можем просто умножить маску на цвет внутреннего огня:
// Calculate portal color
const float3 colorPortalInner = cb4_v5.rgb; // (1.00, 0.60, 0.21961)
...
const float3 portal_inner_final = pow(colorPortalInner, 2.2) * inner_influence; Ассемблерный код:
155: log r2.xyz, cb4[5].xyzx
156: mul r2.xyz, r2.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
157: exp r2.xyz, r2.xyzx
...
170: mad r2.xyz, r2.xyzx, r1.zzzz, r3.xyzx Вот видео, в котором демонстрируются отдельные слои внутреннего огня. Порядок: первый слой, второй слой, внутреннее влияния и окончательный внутренний цвет:
3.2. Свечение
Создав внутренний огонь, переходим ко второму слою: свечению. Вот видео, демонстрирующее сначала только внутренний огонь, потом только свечение, а затем их сумму — готовый эффект огня:
Вот как шейдер вычисляет свечение. Аналогично созданию внутреннего огня, сначала генерируется маска, которая затем умножается на цвет свечения из буфера констант.
const float portalOuterGlowAttenuation = cb4_v10.x; // 0.30
const float portalOuterColorBoost = cb4_v11.x; // 1.50
const float3 colorPortalOuterGlow = cb4_v12.rgb; // (1.00, 0.61961, 0.30196)
...
// Calculate outer portal glow
float outer_glow_influence;
{
float outer_mask = (1.0 - backMask) * innerMask;
const float perturbParam = fire1*fire1;
float outer_mask_perturb = lerp( 1.0 - portalOuterGlowAttenuation, 1.0, perturbParam );
outer_mask *= outer_mask_perturb;
outer_glow_influence = outer_mask * portalOuterColorBoost;
}
// the final glow color
const float3 portal_outer_final = pow(colorPortalOuterGlow, 2.2) * outer_glow_influence;
// and the portal color, the sum of fire and glow
float3 portal_final = portal_inner_final + portal_outer_final;Вот как выглядит outer_mask:
(1.0 — backMask) * innerMask

Свечение не имеет постоянного цвета. Чтобы оно выглядело интереснее, используется анимированный первый слой огня (в квадрате), поэтому заметны идущие к центру колебания:

Вот ассемблерный код, отвечающий за свечение:
158: add r2.w, -v1.z, l(1.000000)
159: mul r2.w, r2.w, v1.y
160: mul r1.w, r1.w, r1.w
161: add r3.x, l(1.000000), -cb4[10].x
162: add r3.y, -r3.x, l(1.000000)
163: mad r1.w, r1.w, r3.y, r3.x
164: mul r1.w, r1.w, r2.w
165: mul r1.w, r1.w, cb4[11].x
166: log r3.xyz, cb4[12].xyzx
167: mul r3.xyz, r3.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000)
168: exp r3.xyz, r3.xyzx
169: mul r3.xyz, r1.wwww, r3.xyzx
170: mad r2.xyz, r2.xyzx, r1.zzzz, r3.xyzx 3.3. Марево
Когда я начал анализировать реализацию шейдера портала, мне было непонятно, почему в качестве одной из входящих текстур используется цвет сцены без портала. Я рассуждал так — «здесь мы используем смешение, поэтому достаточно возвращать пиксель с нулевым значением альфы, чтобы сохранить цвет фона».
Шейдер имеет небольшой, но красивый эффект марева (теплового искажения воздуха) — от портала исходят тепло и энергия, поэтому фон искажён.
Принцип заключается в смещении texcoords пикселя и сэмплировании текстуры цвета фона с новыми координатами — такую операцию невозможно выполнить простым смешением.
Вот видео с демонстрацией того, как это работает. Порядок: сначала полный эффект, потом марево из шейдера, а в конце я умножаю смещение на 10, чтобы усилить эффект.
Давайте посмотрим, как вычисляется смещение.
const float ViewSpaceDepth = Input.ViewSpaceDepth;
const float3 Tangent = Input.Tangent;
const float backgroundDistortionStrength = cb4_v1.x; // 0.40
// Fades smoothly from the outer edges to the back of a portal
const float heatHazeMask = Input.Color.x;
...
// The heat haze effect is view dependent thanks to tangent vectors in view space.
float2 heatHazeOffset = mul( normalize(Tangent), (float3x4)g_mtxView);
heatHazeOffset *= float2(-1, 1);
// Fade the effect as camera is further from a portal
const float heatHazeDistanceFade = backgroundDistortionStrength / ViewSpaceDepth;
heatHazeOffset *= heatHazeDistanceFade;
heatHazeOffset *= heatHazeMask;
// this is what animates the heat haze effect
heatHazeOffset *= pow(fire1, 0.2);
// Actually I don't know what's this :)
// It was 1.0 usually so I won't bother discussing this.
heatHazeOffset *= vsDepth2; Соответствующий ассемблер разбросан по коду:
11: dp3 r1.x, v3.xyzx, v3.xyzx
12: rsq r1.x, r1.x
13: mul r1.xyz, r1.xxxx, v3.xyzx
14: mul r1.yw, r1.yyyy, cb12[2].xxxy
15: mad r1.xy, cb12[1].xyxx, r1.xxxx, r1.ywyy
16: mad r1.xy, cb12[3].xyxx, r1.zzzz, r1.xyxx
17: mul r1.xy, r1.xyxx, l(-1.000000, 1.000000, 0.000000, 0.000000)
18: div r1.z, cb4[1].x, v0.z
19: mul r1.xy, r1.zzzz, r1.xyxx
20: mul r1.xy, r1.xyxx, v1.xxxx
...
33: mul r1.xy, r1.xyxx, r2.xxxx
34: mul r1.xy, r0.zzzz, r1.xyxxМы вычислили смещение, так давайте его используем!
const float2 backgroundSceneMaxUv = cb0_v2.zw; // (1.0, 1.0)
const float2 invViewportSize = cb0_v1.zw; // (1.0 / 1920.0, 1.0 / 1080.0 )
// Obtain background scene color - we need to obtain it from texture
// for distortion effect
float3 sceneColor;
{
const float2 sceneUv_0 = pixelUv + backgroundSceneMaxUv*heatHazeOffset;
const float2 sceneUv_1 = backgroundSceneMaxUv - 0.5*invViewportSize;
const float2 sceneUv = min(sceneUv_0, sceneUv_1);
sceneColor = texScene.SampleLevel(sampler6, sceneUv, 0).rgb;
} 175: mad r0.xy, cb0[2].zwzz, r1.xyxx, r0.xyxx
176: mad r1.xy, -cb0[1].zwzz, l(0.500000, 0.500000, 0.000000, 0.000000), cb0[2].zwzz
177: min r0.xy, r0.xyxx, r1.xyxx
178: sample_l(texture2d)(float,float,float,float) r1.xyz, r0.xyxx, t6.xyzw, s6, l(0) Итак, в конечном итоге мы получили sceneColor.
3.4. Цвет «цели» портала
Под цветом «цели» я подразумеваю центральную часть портала:

К сожалению, он весь чёрный. И причиной этого является туман.
Я уже рассказывал о том, как реализован туман в этой статье. В шейдере портала вычисления тумана находятся в строках [35-135] исходного ассемблерного кода.
HLSL:
struct FogResult
{
float4 paramsFog;
float4 paramsAerial;
};
...
FogResult fog;
{
const float3 CameraPosition = cb12_v0.xyz;
const float fogStart = cb12_v22.z; // near plane
fog = CalculateFog( WSPosition, CameraPosition, fogStart, false );
}
...
const float3 destination_color = fog.paramsFog.a * fog.paramsFog.rgb; И таким образом мы получаем готовую сцену:

Дело в том, что камера в кадре находится так близко к порталу, что вычисляемый destination_color равен нулю, то есть чёрный центр портала на самом деле является туманом (или, строго говоря, его отсутствием).
Так как при помощи RenderDoc мы можем инъектировать в игру шейдеры, давайте попробуем сместить камеру вручную:
const float3 CameraPosition = cb12_v0.xyz + float3(100, 100, 0); И вот результат:

Ха!
Итак, хотя в этом конкретном случае очень мало смысла использовать вычисления тумана, теоретически ничто не мешает нам использовать в качестве destination_color . например, ландшафт из другого мира (возможно, потребуется дополнительная пара texcoords, но, тем не менее, это вполне реализуемо).
Использование тумана может быть полезным в случае огромного портала, который игрок может увидеть с большого расстояния.
3.5. Смешение цвета сцены (с наложенным маревом) с «целью»
Я раздумывал, куда поместить этот раздел — в «Цвет „цели“» или «Собираем всё вместе», но решил создать новый подраздел.
Итак, на этом этапе у нас есть описанный в 3.3 sceneColor, уже содержащий эффект марева (теплового искажения), а также есть destination_color из раздела 3.4.
Они интерполируются при помощи:
178: sample_l(texture2d)(float,float,float,float) r1.xyz, r0.xyxx, t6.xyzw, s6, l(0)
179: mad r3.xyz, r4.wwww, r4.xyzx, -r1.xyzx
180: mad r0.xyw, r0.wwww, r3.xyxz, r1.xyxz Что за значение, которое их интерполирует (r0.w)?
Здесь применяется текстура шума/дыма.
Она используется для создания того, что я называю «маской цели портала».

Вот видео (сначала полный эффект, затем маска цели, затем интерполированные подвергнутый мареву цвет сцены и цвет цели):
Взгляните на этот фрагмент на HLSL:
// Determines the back part of a portal
const float backMask = Input.Color.z;
const float ViewSpaceDepth = Input.TexcoordAndViewSpaceDepth.z;
const float viewSpaceDepthScale = cb4_v0.x; // 0.50
...
// Load depth from texture
float hardwareDepth = texDepth.SampleLevel(sampler15, pixelUv, 0).x;
float linearDepth = getDepth(hardwareDepth);
// cb4_v0.x = 0.5
float vsDepthScale = saturate( (linearDepth - ViewSpaceDepth) * viewSpaceDepthScale );
float vsDepth1 = 2*vsDepthScale;
....
// Calculate 'portal destination' mask - maybe we would like see a glimpse of where a portal leads
// like landscape from another planet - the shader allows for it.
float portal_destination_mask;
{
const float region_mask = dot(backMask.xx, vsDepth1.xx);
const float2 _UVScale = float2(4.0, 1.0);
const float2 _TimeScale = float2(0.0, 0.2);
const float2 _UV = texcoords * _UVScale + elapsedTime * _TimeScale;
portal_destination_mask = texNoise.Sample(sampler0, _UV).x;
portal_destination_mask = saturate(portal_destination_mask + region_mask - 1.0);
portal_destination_mask *= portal_destination_mask; // line 143, r0.w
} Маска цели портала в целом получается так же, как огонь — при помощи анимированных координат текстуры. Для настройки местоположения эффекта используется переменная «region_mask«.
Для получения region_mask используется ещё одна переменная под названием vsDepth1. Чуть подробнее я опишу её в следующем разделе. Впрочем, она имеет незначительное влияние на маску цели.
Ассемблерный код маски цели выглядит так:
137: dp2 r0.w, v1.zzzz, r0.zzzz
138: mul r2.xy, cb0[0].xxxx, l(0.000000, 0.200000, 0.000000, 0.000000)
139: mad r2.xy, v0.xyxx, l(4.000000, 1.000000, 0.000000, 0.000000), r2.xyxx
140: sample_indexable(texture2d)(float,float,float,float) r2.x, r2.xyxx, t1.xyzw, s0
141: add r0.w, r0.w, r2.x
142: add_sat r0.w, r0.w, l(-1.000000)
143: mul r0.w, r0.w, r0.w 3.6. Соединяем всё вместе
Фух, почти закончили.
Давайте сначала получим цвет портала:
// Calculate portal color
float3 portal_final;
{
const float3 portal_inner_color = pow(colorPortalInner, 2.2) * inner_influence;
const float3 portal_outer_color = pow(colorPortalOuterGlow, 2.2) * outer_glow_influence;
portal_final = portal_inner_color + portal_outer_color;
portal_final *= vsDepth1; // fade the effect to avoid harsh artifacts due to depth test
portal_final *= portalFinalColorFilter; // this was (1,1,1) - so not relevant
} Единственный аспект, который я хочу здесь обсудить — это vsDepth1.
Вот как выглядит эта маска:

В предыдущем подразделе я показал, как она получается; по сути, это «линейный буфер глубин», используемый для уменьшения цвета портала так, чтобы не было резкой границы из-за теста глубин.
Рассмотрим ещё раз готовую сцену, с умножением и без умножения на vsDepth1.


После создания portal_final получить готовый цвет просто:
const float finalPortalAmount = cb2_v0.x; // 0.99443
const float3 finalColorFilter = cb2_v2.rgb; // (1.0, 1.0, 1.0)
const float finalOpacityFilter = cb2_v2.a; // 1.0
...
// Alpha component for blending
float opacity = saturate( lerp(cb2_v0.x, 1, cb4_v13.x) );
// Calculate the final color
float3 finalColor;
{
// Mix the scene color (with heat haze effect) with the 'destination color'.
// In this particular example fog is used as destination (which is black where camera is nearby)
// but in theory there is nothing which stops us from putting here a landscape from another world.
const float3 destination_color = fog.paramsFog.a * fog.paramsFog.rgb;
finalColor = lerp( sceneColor, destination_color, portal_destination_mask );
// Add the portal color
finalColor += portal_final * finalPortalAmount;
// Final filter
finalColor *= finalColorFilter;
}
opacity *= finalOpacityFilter;
return float4(finalColor * opacity, opacity); Вот и всё. Есть ещё одна переменная finalPortalAmount, определяющая, сколько пламени видит игрок. Я не стал тестировать её подробно, но предполагаю, что она используется, когда портал появляется и исчезает — на короткий промежуток времени игрок не видит огня, зато видит всё остальное — свечение, цвет цели и т.п.
4. Подведём итог
Готовый шейдер на HLSL выложен здесь. Мне пришлось поменять местами несколько строк, чтобы получить тот же ассемблерный код, что и у оригинала, но это не мешает общему потоку выполнения. Шейдер готов к использованию с RenderDoc, все cbuffers присутствуют и т.д, поэтому вы можете его инъектировать и поэкспериментировать самостоятельно.
Надеюсь, вам понравилось, спасибо за прочтение!


