Проблема континуума волновала математиков со времен создателя теории множеств, Кантора. Великий математик Гильберт поставил ее на первое место в своем знаменитом списке. В каком-то смысле она считается решенной — только многие не считают это решением, и она по-прежнему занимает умы философов и математиков.

О мощностях множеств
Напомню, что «размер» бесконечных множеств не может быть определен методом пересчета элементов. Вместо этого используется понятие «мощности множества», которое определяется на основе взаимных отображений элементов. Например, любое бесконечное множество целых чисел (например, множество простых чисел) можно пересчитать, присвоив им номера. Все такие множества имеют мощность алеф-нуль (сорри, строчные формулы испортились на хабре и быстро их не починят, как говорит саппорт)
Множество вещественных чисел, однако, пересчитать нельзя, что доказывается очень элегантно диагональным методом. Мощность множества точек любых конечных и бесконечных фигур на плоскости, в объеме итд также является равномощной множеству вещественных чисел и обозначается ка.
Так как множество формул (конечные строки в конечном алфавите) счетно, то большинство вещественных чисел не имеют никакого представления, это безликая масса, безликая настолько, что несмотря на то, что ‘безликих’ чисел по-прежнему континуум, ни одно из них нельзя привести в пример, показав его явно. Такие безликие элементы называются indiscernibles (замечу, что русской статьи в вики по этому поводу нет, и аналога русского слова мне тоже неизвестно).
Несмотря на то, что из такого множества мы не можем явно предъявить ни одного элемента, для аксиомы выбора нет никаких проблем это сделать. Доказательства, начинающиеся со слов «возьмем произвольный элемент множества» прекрасно работают, если есть аксиома выбора, и поэтому эта аксиома так часто порождает чудовищ — например, парадокс Банаха-Тарского (замечу, что само разрезание сферы в этом парадоксе является indiscernible).
Мы пока познакомились с двумя бесконечными мощностями: счетным и континуумом. Оказывается, есть стандартный способ производить все бОльшие и бОльшие мощности: операция powerset — получение всех подмножеств этого множества. Она обозначается ка.
— действительно, для конечных множеств число элементов увеличивается именно так. Достоверно известно, что
Гипотеза континуума
Первый вопрос, который возникает, и он действительно возник еще у Кантора, есть ли множество с мощностью между счетной бесконечностью и континуумом? То есть
Как ни странно, это оказалось очень сложной задачей, не даром она попала в список задач Гильберта под номером 1. Вначале, много лет спустя, Гедель доказал, что существование такого множества не может быть доказано в стандартной теории множеств. Четверть века спустя Cohen доказал, что это утверждение не может быть и опровергнуто. Таким образом, это утверждение является независимым от теории множеств, что сразу порождает две версии теории множеств — где такое множество существует и где его нет.
Если такое множество есть, то оно является indiscernible, потому что если бы это было бы не так, то мы могли бы доказать его существование, просто приведя пример его построения.
Вот вы зря поверили мне сразу, что таких версий две. Их больше. Во-первых, есть ‘нейтральная’ версия, которая ничего не говорит о существовании множеств промежуточной мощности. Во-вторых, есть версия с гипотезой континуума — она категорична, таких множеств нет. А вот если мы допустим существование множеств промежуточной мощности, то мы можем аксиоматически утверждать, что таких множеств ровно одно, два, три, 188338, любое количество между 17 и 83, любое конечное число, любое конечное простое число итд.
Интересно, что число таких множеств с промежуточной мощностью не может быть бесконечным по довольно сложным причинам. Но любое конечное число — пожалуйста! Допустимо любое конечное подмножество целых, что дает счетное число вариантов теории.
Есть более сильный вариант гипотезы континуума (CH) — обобщенная гипотеза континуума (GCH). Она утверждает, что не только чт.
но что это верно и для любой мощности:
GCH сильнее CH и из нее еще следует AC (аксиома выбора).
Философский аспект
Так что, задача решена? (так она и помечена в списке Гильберта)? Формалиста от математики (это не обзывалка) это решение полностью удовлетворит. Для формалиста мы вольны задавать любые аксиомы, и получать разный результат с разными аксиомами.
Для платониста же такой ответ неудовлетворителен, поскольку математика это отражение высшей реальности универсума, и на самом деле решение есть — да или нет. Мы должны просто найти подходящие аксиомы, где решение будет.
Конечно, можно спросить — так в чем проблема? Прими гипотезу континуума (CH), что множеств промежуточной мощности нет, вот и решение. Но CH — это костыль, объявление желаемого результат аксиомой. Как если бы в забагованной функции, которая иногда выдает NaN, мы бы сделал проверку на это значение и выдавали бы, например, 0.0, не исправляя самого бага.
Но поиск такой аксиомы вещь очень сложная, потому что аксиома должна быть простой и самоочевидной — куда проще чем сама CH.
Гедель был платонистом, и хотел найти решение, поэтому начал поиск в сторону высших мощностей, которые идут з.
и много дальше, за недостижимые мощности. Направление поиска оказалось очень плодотворным. Можно было бы ожидать, что теорию множеств можно «гнуть» в любую сторону, добавляя разные аксиомы. Но, видимо, за формулами все же есть реальность, и платонисты правы — все новые аксиомы нанизывались друг на друга, образуя почти правильную нить, уходящую в бесконечность к абсолютному универсуму.
На одном из уровней, который отделял маленькие большие мощности (small large cardinals) от больших больших мощностей (large large cardinals) почти нашлось решение проблемы.
Вселенные
Мало кто из ученых может похвастаться существованием вселенной, названной его именем. Я знаю только три таких ученых: Фон Нейман, Гретендик и Гедель. Причем у Геделя вселенных аж две. Первая не имеет отношения к математике — это вращающаяся вселенная Геделя, где все вращается вокруг всего.
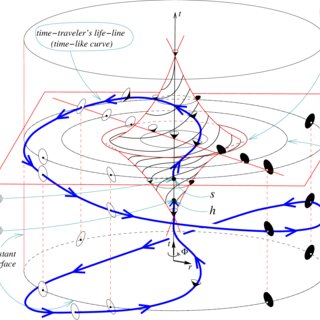
Она является точным решением общей теории относительности для специальных условий. Мало того, что все вращается вокруг всего, так еще и через любую точку пространства времени проходят временной цикл. Создана она была как контрпример принципу Маха. Но мы отвлеклись.
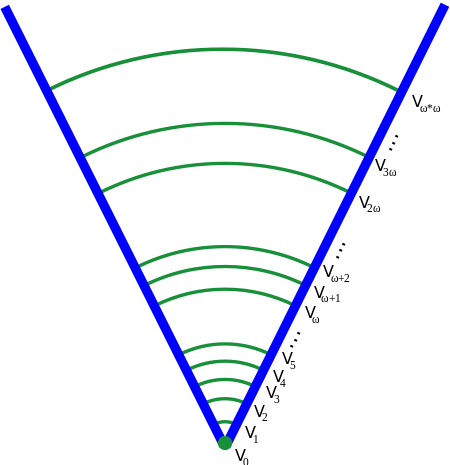
Первая математическая вселенная — это V фон Неймана. Она состоит из уровней, при добавлении нового мы берем множество всех подмножеств. V без индекса означает всю вселенную, то есть класс всех множеств (напомню что множество всех множеств — не множество во всех классических теориях множеств. Исключение — New Foundations)
Вселенную Гротендика пропустим. Гедель придумал вселенную L, которая тоже разворачивается этапами — но используя принцип определимости формулами. Каждый следующий уровень собирается из материала предыдущего используя возможные формулы — комбинации множеств, полученных на предыдущих уровнях. Второе название этой вселенной — конструктивная вселенная.
В чем же разница между L и V? V ничего не говорит о свойствах и количестве элементов и возможности их определить. В L же, по построению, не может быть indiscernibles. Таким образом
Если принять, что V=L, то сразу решаются многие проблемы, например, CH и GCH — ведь в L нет indiscernibles а значит, обе проблемы решаются автоматически.
Но увы, как оказалось, V=L кастрирует иерархию мощностей, убивая большие большие мощности полностью, а это неинтересно. Хотя граница V=L и пролегает очень, очень высоко, выше всего, куда можно забраться с помощью бесконечног.
выше недостижимых мощностей, выше гипер-гипер-недостижимых и еще много выше. Но этого мало.
Даже сам Гедель тоже не верил, что V=L. Увы, надежда оказалась ложной. А жаль, потому что L обладает рядом удобных свойств. Например, все множества в ней определяются одной или несколькими формулами. Мы можем выбрать самую короткую и отсортировать все множества в однозначном порядке. А еще множеств в ней счетное количество, так как множество всех формул счетно.
Что простите?
Парадокс Скулема
Что же такое получается? Мы говорили о несчетных множествах, шли все выше и выше, получали множества чудовищной мощности и теперь оказывается, что всего всех множеств счетное число?
Да, в L это так. Это носит название парадокса Скулема. Теории первого порядка фатально не умеют контролировать мощность своих моделей. Если у теории есть бесконечная модель, то есть модели любой бесконечной мощности.
Модель — это набор «фишек», который удовлетворяет всем формулам теории.

Но давайте разберемся в парадоксе. Итак, есть множество континуума, которой говорит «Йа несчетно«. Мы говорим (в L): а ну-ка, покажи, кто в тебя входит, типа list() в Python. Система задумалась и сгенерила бесконечную строку формул — определений множеств, которые в него входят. Но их счетное количество! Как такое может быть?
Формально парадокс кажущийся, так как утверждение о несчетности множества существует внутри теории, а фишки мы пересчитываем вовне. Это два разных уровня реальности. Но вряд ли вы полностью удовлетворены этим ответом.
Тогда вы можете считать, что определимые элементы в L — это «реперные» точки, которые нарисованы на кривых. Всего точек куда больше, но нам достаточно этих реперных точек.
С вещественными числами все то же самое — мы всегда имеем дело со счетным количеством и обычно этого достаточно, если остальные точки (indiscernibles) ведут себя достаточно мирно. Но это не всегда так, аксиома выбора позволяет построить подмножество вещественных чисел, которое нельзя измерить. Многие чудовища прячутся в тени среди indiscernibles, куда не проникает наш взгляд.
Именно поэтому ни Гедель, ни большинство других математиков не верят в V=L, потому что эта гипотеза делает мир слишком примитивным.
Поздние исследования
Вильям Вудин еще в 90х годах пытался ближе подойти к решению проблемы гипотезы континуума. Сначала он принялся оперировать бесконечной логикой — логикой, где формулы могут быть бесконечной длины, адаптировав ее к теории множеств. Далее он выдвинул правдоподобную гипотезу, которая, если ее принять, решает CH в негативном, но определенном ключе.
то есть между счетной мощностью и мощностью континуума есть ровно одна мощность.
К сожалению, ни бесконечная логика, ни сама гипотеза не удовлетворяют принципу, что аксиома не должна быть, как минимум, сложнее утверждения, которую она доказывает. Вот саму гипотезу континуума понять несложно, а то что написал Вудин я понимаю только по самым верхам. Позже Вудин сам отошел от своей гипотезы и пошел в другом направлении.
Он попытался так расширить L, чтобы V=L не усекала вселенную на таком низком уровне, а содержала почти все большие-большие мощности. Чтобы было лучше понятно, приведу картинку устройства вселенных:

Черный конус — это вселенная V. Для конечных множеств она совпадает с L, но она Уже и ниже V. Она обрывается на уровне аксиомы V=L, убивая интересные большие большие мощности. Вудин пытается создать расширенную вселенную Ultimate-L, которая много выше. Граница V=L отделяет «малые» большие мощности от «больших» больших мощностей.
Выше красной линии находятся «безумно большие большие» мощности. Они столь велики, что там уже перестает работать аксиома выбора AC (а значит и GCH, следовательно, CH там точна ложна!). Но последние исследования Вудина намекают, что там сбоит не только AC, но и ее более простые и куда более очевидные варианты. То есть там живут монстры и, возможно, вся эта конструкция противоречива.
Вудин надеется, что его Ultimate-L решит CH в положительном ключе (то есть от поменял свое мнение)
А зачем вот это все?
Заметьте, что практически вся математика на поднимается выше первых двух бесконечных мощностей — счетного и континуума. С натяжкой, когда мы говорим о подмножествах вещественных чисел мы поднимаемся на уровень второго алефа. Даже первая необычная (сингулярная) мощност.
нигде не появляется в обычной математике.
Мне известно только три случая, когда существование высших мощностей влияло на что-то вне теории множеств:
-
не так давно выяснилось, что некоторые аспекты машинного обучения зависят от гипотезы континуума
-
некоторые свойства очень быстрорастущих функций доказываются с помощью аксиом существования высоких мощностей — пример
-
неограниченность роста периода laver tables доказывается с помощью аксиомы одной из самых высоких мощностей — однако я думаю что функция растет не настолько быстро, чтобы превысить предел доказуемых утверждений в формальной арифметике — возможно, есть простое доказательство, не использующее теорию множеств.
Так на что это все влияет? Вудин в одной из своих лекций сказал, что есть два варианта: либо когда-нибудь вся эта математика потребуется в Теории Всего, либо нет. Согласитесь, первые вариант был бы интересным — можно себе представить, что, например, в формулу для отношения массы верхнего кварка к нижнему пробрался коэффициент, равный 1, если гипотеза континуума верна и 0 в противном случае.
Но может быть и так, что вся эта кухня никак к физике отношения не имеет. Вудин считает, что это тоже оптимистичный вариант! Потому что это означает, что мы, люди, увидели нечто (очевидно, Вудин платонист), что лежит вне нашей вселенной. От себя добавлю, что это очень перекликается с Гипотезы Математической Вселенной (MUH), созданной Максом Тегмарком.


