Что такое температура и как её учитывать в молекулярном моделировании? Реализация на CUDA

Методы численного моделирования молекулярных систем, такие как молекулярная динамика, рассматривают эти системы как механические (что-то вроде набора шариков на пружинках). Однако, в отличие от механических систем, для молекулярных существует понятие температура. Вещество не может существовать без температуры, а температура – без вещества (на счет последней части утверждения есть и другое мнение). Из опыта мы знаем, что очень многие свойства вещества кардинально зависят от температуры, и, естественно, что её надо как-то учитывать. Для поддержания температуры в молекулярной динамике используются специальные алгоритмы-«термостаты». Наиболее известные среди них это термостаты Андерсена, Берендсена и Нозе-Гувера. Все они основаны на молекулярно-кинетической теории газов, где температура есть просто величина пропорциональная среднекинетической энергии молекул. Соответственно, работа данных термостатов осуществляется путём умножения скоростей частиц на некоторую величину.

Что же не так?

1. Масштабирование скоростей изменяет их модуль, но не направление. А ведь тепловое движение, согласно большинству утверждений, должно быть хаотическим. Оно определяет броуновское движение. Термостатирование в молекулярной динамике же не привносит никакого хаоса, частицы движутся в том же направлении, как и без учета температуры, только быстрее/медленнее. Метод остается полностью детерминированным, начальные координаты и скорости частиц полностью определяют конечное состояние.

2. Скорости определяются через интегрирование уравнений движения, из ускорений – а ускорения – из сил. Силы задаются потенциалами, которые позиционируются как имеющие смысл. Получается мы сначала выбрали потенциал, через него определили как частицы взаимодействуют, начали вычислять ускорения и скорости, а потом взяли эти скорости и домножили на какую-то величину. Какой тогда смысл в потенциалах?

3. Связь температуры и кинетической энергии выводится из основных положений МКТ, которые верны только для идеального газа. Наиболее близкими к идеальному газу реальные системы – это благородные газы при высоких температурах и низких давлениях. Проиллюстрировать неуниверсальность МКТ можно простым примером: при одной температуре средняя кинетическая энергия атомов в твердом теле и в газе должна быть одинаковой, что не кажется правдоподобным.

Модель

Чтобы сконструировать корректный термостат нам нужно разобраться, а что же такое температура на самом деле? Несмотря на то, что мы этим понятием оперируем чуть ли не с дошкольного возраста, суть температуры, как мне кажется, до конца не ясна.

Соберем известные факты о температуре:

• Температура не может быть ниже «абсолютного нуля», т.е. 0 К.

• Температура – понятие интенсивное, оно не зависит от размеров системы, количества вещества и т.д.

• Температура имеет свойство выравниваться – если мы приведем в контакт два тела разной температуры (даже можно и без контакта, тела могут обмениваться излучением), то рано или поздно температура обоих тел станет одинаковой.

• Скорости химических реакций и коэффициенты диффузии с температурой растут экспоненциально.

• При повышении температурах сложные вещества постепенно разлагаются на более простые.

• Агрегатные состояния с повышением температуры меняются как правило в порядке: твердое, жидкое, газообразное. При этом тепло почти всегда поглощается (единственное известное исключение – гелий, его энтальпия плавления отрицательная). При очень высоких температурах начинается ионизация газа (молекулы/атомы газа теряют электроны).

• С увеличением температуры тела обычно расширяются (газы – все, твердые тела – почти все, но есть исключения, см. отрицательный КТР).

• Теплоемкость с температурой как правило растет (для некоторых жидкостей, такие как расплавленные оксиды она постоянная или чуть падает).

• С температурой связан интересный эффект, адиабатическое расширение в пустоту (эффект Джоуля-Томсона).

• Другой интересный эффект, сонолюминисценция – воздействие ультразвуком приводит к разогреванию жидкости (воды) до температуры в десятки тысяч кельвинов. На хабре, кстати, была статья про неё.

• С увеличением температуры растет сжимаемость, т.е. при высоких температурах чтобы сжать тело в то же число раз, нужно приложить меньшее давление. По крайней мере, это верно для расплавов.

• Электропроводность металлов падает с температурой.

• Спектр излучения абсолютно черного тела определяется исключительно его температурой.

Как мы видим, количественных характеристик температуры не так уж и много. Привязываться к каким-то «ключевым точкам» типа температуры кипения воды не имеет смысла, поскольку: они очень частные; зависят и от других условий, в первую очередь, давления. Тем не менее, есть характеристика, кажущаяся довольно перспективной. Это спектр излучения абсолютно черного тела. Оказывается, если тело ничего не отражает, а все излучение от него является «собственным», то спектр этого излучения не зависит от природы объекта, а определяется исключительно его температурой, согласно формуле Планка. Тот факт, что все тела излучают и характеристики этого излучения зависят от температуры используется, например, в оптической пирометрии. Таким образом, температуру можно определить через спектр излучения. В условии равновесия с термостатом, т.е. средой, имеющей заданную температуру, излучение, испускаемое объектом, должно сравняться с излучением термостата. Тогда можно реализовать термостатирование следующим образом: атомы поглощают и испускают фотоны в случайном направлении, при этом их скорости изменяются согласно закону сохранения импульса. Интуитивно кажется, что если мы будем прибавлять/убавлять поправку к скорости атома в случайном направлении, то атом сначала наберет какую-то скорость, а затем эта скорость выйдет на насыщение, поскольку все выше вероятность того, что новая скорость будет направлена против одной из предыдущих добавок. Однако легко показать, что это не так, начнем с закона сохранения импульса:

где m и v – масса и скорость атома, индексы 1 и 0 означают состояния до и после поглощения фотона, p_γ – импульс фотона. Перейдем к скоростям:

где ε – энергия фотона, c – скорость света в вакууме, r – единичный вектор случайного направления. Из этого, квадрат скорости равен:

или, используя определение скалярного произведения векторов:

где φ – угол между начальной скоростью атома и направлением движения поглощенного фотона. Косинус принимает значения от -1 до 1, а в среднем ноль, тогда мы видим, что среднее приращение квадрата скорости (что пропорционально кинетической энергии)

положительное. Т.е. действуя таким образом, мы будем накачивать систему кинетической энергией, независимо от того будем излучать или поглощать фотоны, поскольку знак будет стоять перед косинусом, который в среднем нулевой. Чтобы скомпенсировать неограниченный рост скоростей в системе нужно, чтобы среднее изменение квадрата скорости атома при излучении фотона было равно среднему значению изменения квадрата скорости при поглощении фотона (5) с обратным знаком:

для этого косинус между направлением движения атома и изулучаемым фотоном, в среднем, должен равняться:

Это выражение устанавливает связь между скоростями атомов и энергией фотонов. Можно задать косинус φ равномерной случайной величиной, так чтобы указанное выше значение было серединой интервала, а -1 – его нижней границей.

Вторая проблема возникает с законом сохранения энергии. Если мы допустим, что вся энергия фотона полностью перейдет в кинетическую энергию атома, то должно выполняться равенство:

однако, если мы попытаемся решить уравнение в системе с законом сохранения импульса (2), мы получим нефизичный результат. Например, покоящийся атом должен разогнаться до световой скорости. Причина этого заключается в том, при одном порядке кинетической энергии атома и энергии фотона их импульсы отличаются на несколько порядков. Решение напрашивается следующее: импульс сохраняем, вычисляем изменение кинетической энергии, оставшийся избыток энергии фотона добавляем к какой-нибудь другой энергии атома, назовём её «тепловой» (обозначим U):

где K – кинетическая энергия. Остался вопрос, фотоны какой энергии излучать атому? Давайте немного упростим модель, пусть тепловое излучение описывается не формулой Планка, а будет монохроматическим, с длиной волны / частотой / энергией однозначно определяемыми температурой. Для этого подходит, например, закон Вина, определяющий длину волны, дающую наибольший вклад в спектр излучения:

где λ – длина волны в метрах, от длины волны несложно перейти к энергии фотона, дробь при этом перевернется и в общем случае можно записать:

где γ – некоторый постоянный коэффициент. Т.е. температура T, это такое состояние вещества, когда излучаются фотоны энергией γT.

Кроме того, у нас есть ещё одна численная характеристика, касающаяся температуры. Мы совершенно точно знаем, какое количество теплоты (энергии/тепловой энергии) нужно сообщить телу, чтобы нагреть его до заданной температуры от нуля кельвинов. В условиях постоянного давления эта величина называется приращением энтальпии / инкрементом энтальпии / энтальпией (не путать с энтальпией образования), её значение зависит не только от температуры, но и от природы вещества. Если приводить образную аналогию, то вещество можно представить как сосуды с некой жидкостью, где её уровень – это температура, а объём – энтальпия. Производная энтальпии по температуре называется изобарной теплоемкостью, c_p. Для идеального газа (и, с некоторым приближением, для благородных газов) c_p постоянна, тогда:

Объединяя (11) и (12) можно исключить температуру и получить энергию фотона как функцию от текущей тепловой энергии, запасенной в веществе:

Мы получили, что энергия излучаемых фотонов определяется энтальпией вещества. Продолжая нашу аналогию с сосудами, можно представить, что они теряют жидкость пропорционально высоте столба. Напоминаю, что выражение (13) справедливо только для систем с постоянной теплоемкостью, для реальных систем нужно находить температуру как функцию от энтальпии и подставлять её в (11). При переходе к числам меня ждал сюрприз, выразив из (10) значение γ и подставив его в (13), а c_p взяв равным 5/2k (изобарная теплоемкость одноатомного идеального газа) получилось, что коэффициент перед энтальпией больше 1, а это означает, что система должна излучать больше энергии, чем имеется, что, конечно, не физично. Немного покопавшись, я нашел, что при переходе от длины волны к частоте (и затем к энергии) нужно использовать несколько отличное выражение, чем (10). В конечном итоге, с использованием данных по теплоемкости гелия, у меня получилось, γ/c_p ≈ 0.9, что я и взял для своих численных экспериментов. В качестве энтальпии я взял величину U, описанную выше, формула (9).

Немного кода

Основная часть кода базируется на изложенном ранее. Однако вместо термостата Нозе-Гувера используется вышеописанная схема. Функция термостатирования:

__global__ void tstat_radi(int atPerBlock, int atPerThread, cudaMD* md)
{
    __shared__ int indEng;
    __shared__ float engTemp;
    if (threadIdx.x == 0)
    {
        indEng = atomicAdd(&(md->curEng), 1);   // get current index in photon energies array
        engTemp = 0.f;
    }
    __syncthreads();
    uint4 randVar = md->ui4rnd;

    float pe;        // photon energy
    int i, e0, ei;	// indexes

    // atomic range
    int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
    int N = min(id0 + atPerThread, md->nAt);
    e0 = indEng * atPerBlock + threadIdx.x * atPerThread - id0;

    for (i = id0; i < N; i++)
    {
        ei = e0 + i;
        if (ei >= md->nAt)
            ei -= md->nAt;
        pe = md->engPhotons[ei];

        adsorb_rand_photon(&(md->vls[i]), &(md->engs[i]), md->masses[i], pe, randVar, md);
        radiate_photon(&(md->vls[i]), &(md->engs[i]), md->masses[i], randVar, md);
    }

    atomicAdd(&engTemp, teng);
    if (threadIdx.x == 0)
    {
        rnd_xor128(md->ui4rnd);
        atomicAdd(&(md->engTemp), engTemp);
    }
}

Функция принимает на вход число атомов в потоке и блоке, а также указатель на структуру, где хранятся все МД-данные. Для каждого атома в обрабатываемом диапазоне находится энергия случайного фотона, вызываются функции его поглощения и функция излучения. Энергия поглощаемого фотона берется из предварительно сгенерированного массива энергий, которое соответствует Планковскому распределению (эта часть вычисляется на хосте и загружается в массив). Я здесь использовал ту фичу CUDA, что порядок выполнения блоков не определён. Первый запустившийся блок берет первый кусок массива энергий фотонов и т.д., таким образом получается что-то вроде рандомизации. Таким же образом я хотел сделать и направления фотонов, но рандомизация выходит слабенькой, поскольку порядок выполнения блоков хоть и не определен, но все-таки даёт очень небольшой разбег, для направлений это критично, даёт заметные артефакты.

Функция поглощения фотона принимает на вход указатель на скорость атома, указатель на тепловую энергию атома / энтальпию, массу атома, энергию фотона, переменную для генератора случайных чисел и указатель на главную структуру:

__device__ void adsorb_rand_photon(float3 *vel, float *int_eng, float mass, float eng, uint4 &rand_var, cudaMD *md)
{
    float u0 = *int_eng;
    float v02 = float3_sqr(*vel);   // square of initial velocity
    float3 rand_vect = rand_uvect(rand_var, md);

    // momentum conservation:
    float ermc = eng * revLight / mass;
    vel->x += ermc * rand_vect.x; 
    vel->y += ermc * rand_vect.y;
    vel->z += ermc * rand_vect.z;

    float v12 = float3_sqr(*vel);
    // energy conservation: old kinetic energy + photon energy = new kinetic energy + 'internal' energy
    *int_eng += eng + 0.5f * mass * (v02 - v12);
}

функция rand_uvect берет единичный вектор случайного направления, revLight – константа, обратная скорость света во в единицах программы. Функция излучения фотона принимает на вход указатель на скорость атома, указатель на тепловую энергию атома / энтальпию, массу атома, переменную для генератора случайных чисел и указатель на главную структуру:

__device__ void radiate_photon(float3* vel, float* int_eng, float mass, uint4& rand_var, cudaMD* md)
{
    float u0 = *int_eng;
    float v02 = float3_sqr(*vel);   // square of initial velocity
    float v0 = sqrt(v02);           // module of initial velocity

    float ph_eng = 0.9f * u0;
    float ermc = ph_eng * revLight / mass;

    // random radiation
    float3 rand_vect;
    // random cosine between   (1-2a/v0) .. -1 with mean = -a/v0, where a = e/mc
    float ermcv0 = ermc / v0;       // ph_eng/(m*c*v0)
    float cos_phi;
    if (ermcv0 >= 1.f)
        cos_phi = -1.f;
    else
    {
        int rnd = rnd_xor128(rand_var) % 2048;
        float cos_phi = (float)rnd / 1024.f * (1.f - ermcv0); // 1024, because factor of 2  
        cos_phi -= 1.f;
        rnd = rnd_xor128(rand_var) % 2048;
        float theta = (float)rnd / 1024.f * numPi;  // 0 .. 2PI
        rand_vect = get_angled_vector(*vel, cos_phi, theta);
    }

    // momentum conservation:
    vel->x += ermc * rand_vect.x;   
    vel->y += ermc * rand_vect.y;
    vel->z += ermc * rand_vect.z;

    float v12 = float3_sqr(*vel);
    // energy conservation:
    *int_eng -= (ph_eng + 0.5f * mass * (v12 - v02));
}

Тут учитывается, что выражение (7) может дать и косинус меньше -1, что нужно пофиксить. Поскольку в 3-мерном пространстве векторов, находящихся под заданным углом к данному, целый конус, функция get_angled_vector вычисляет один из них, по выбранному углу вращения:

__device__ float3 get_angled_vector(float3 invec, float cos_phi, float theta)
{
    float3 v1, v2, v3;
    float leng1 = float3_length(invec);

    // only for non-zero input vectors!
    v1 = make_float3(invec.x / leng1, invec.y / leng1, invec.z / leng1);

    // find v2 perpendicular to v1
    if (v1.x != 0.f)
    {
        v2.y = 1.f; v2.z = 1.f; // any coordinates
        v2.x = -(v1.y * v2.y + v1.z * v2.z) / v1.x;
    }
    else
        if (v1.y != 0.f)
        {
            v2.x = 1.f; v2.z = 1.f; // any coordinates
            v2.y = -(v1.z * v2.z) / v1.y;     // a1 = 0 !
        }
        else // a1=0, b1=0, c1 <> 0:
        {
            v2.x = 1.f; v2.y = 0.f; v2.z = 0.f;
        }

    // v3 is perpendicular to both v1 and v2
    v3.x = v1.y * v2.z - v1.z * v2.y;
    v3.y = -v1.x * v2.z + v1.z * v2.x;
    v3.z = v1.x * v2.y - v1.y * v2.x;

    // convert v2 and v3 into unit vectors
    float leng2 = float3_length(v2);
    float leng3 = float3_length(v3);
    v2.x /= leng2;
    v2.y /= leng2;
    v2.z /= leng2;
    v3.x /= leng3;
    v3.y /= leng3;
    v3.z /= leng3;

    float sinPhi, sinTh, cosTh;
    sinPhi = sqrt(1 - cos_phi * cos_phi);
    sincos(theta, &sinTh, &cosTh);

    // parameteric equation of circle
    float x = v1.x * cos_phi + sinPhi * (cosTh * v2.x + sinTh * v3.x);
    float y = v1.y * cos_phi + sinPhi * (cosTh * v2.y + sinTh * v3.y);
    float z = v1.z * cos_phi + sinPhi * (cosTh * v2.z + sinTh * v3.z);

    float3 res = make_float3(x, y, z);
    return res;
} 

Генератор случайных чисел на CUDA не тривиальная задача, спасибо пользователю @denglide за обзор генераторов и пользователю @maratyszcza за xorShift генератор, который и был использован в данной работе.

Предвижу замечание, что функции поглощения и излучения фотона хорошо было бы объединить в одну функцию, поскольку идёт обращение к одним и тем же адресам, но на этапе перебора различных вариантов я разделил эти функции для удобства работы.

Результаты

Ну а теперь к численным экспериментам. В качестве модельного объекта я взял 40’000 атомов аргона, взаимодействующих согласно парному потенциалу из этой работы. Размеры бокса выбраны таким образом, чтобы плотность системы соответствовали плотности аргона при стандартных условиях (T = 298 К и P = 1 атм). Все приведенные результаты даны для 1 млн шагов интегрирования с шагом интегрирования 1 фс. Вычисления проводил на видеокарте GeForce RTX 2080 Ti.

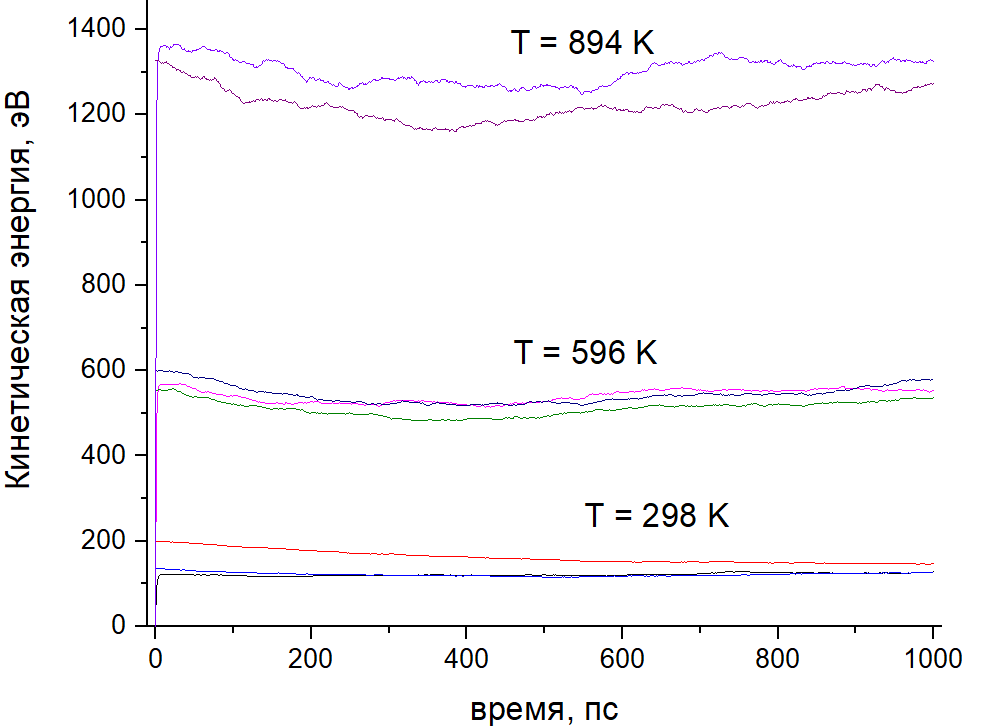
Рис. 1. Зависимость кинетической энергии от времени эволюции системы

Ещё раз напоминаю, что целевую температуру я задаю через набор энергий фотонов, излучаемых термостатом. На данном этапе я следил за изменением кинетической энергии системы (рис. 1) при различных температурах термостата и разных вариантов начальных скоростей атомов. В ряде случаев начальные скорости были нулевыми (E_kin = 0), в других случаях были для всех атомов одинаковыми по модулю, но направленными хаотично (E_kin > 0). Независимо от величины начальных скоростей, кинетическая энергия выходила на примерно постоянное значение, зависящее от температуры термостата, т.е. такой термостат умеет разгонять или замедлять атомы, в зависимости от текущего состояния системы и целевой температуры, что в первую очередь от него и требуется.

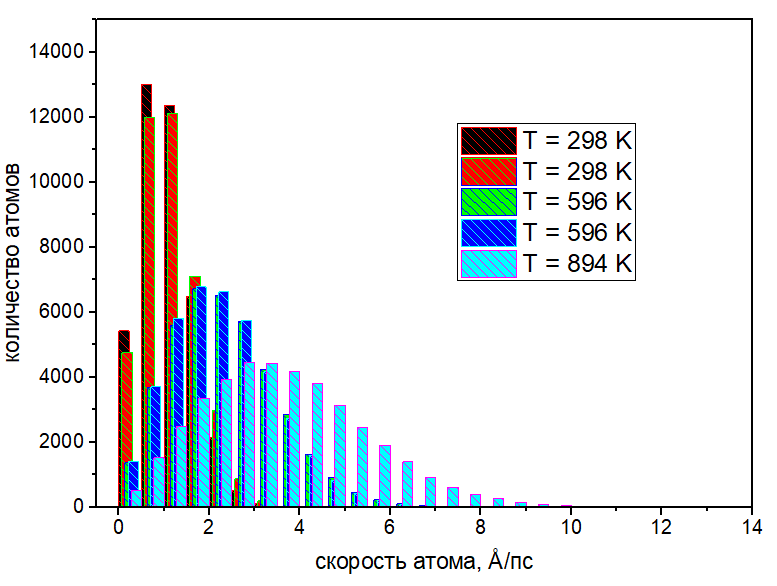
Рис. 2. Распределение атомов по скоростям после 1млн шагов эволюции системы.

Второе, на что я обратил внимание, это распределение скоростей атомов, после 1 млн шагов, рис. 2. Несмотря на то, что начальные скорости были заданы одинаковыми по модулю, в результате работы термостата распределение атомов по скоростям приобрело вид, очень похожий на распределение Максвелла. Точно также как и в распределении Максвелла, меньшая температура соответствует более узкому пику. То, что такое распределение получилось само собой, при выполнении простых правил, я считаю определенным успехом.

Заключение

В качестве заключения кратко суммирую плюсы и минусы полученного способа задания температуры.

Плюсы предложенного термостата:

1. На атомы воздействуют случайные импульсы, так что тепловое движение приобретает хаотический характер, в соответствии с общими представлениями.

2. Распределение скоростей частиц в системе приобретает вид распределения Максвелла.

3. Вычислительная сложность порядка O(N), как у других термостатов.

4. Температура определяет скорости частиц, но не сводится к ним.

5. Есть возможность учитывать индивидуальные свойства разных веществ, используя их температурную зависимость энтальпии (вернее энтальпийную зависимость температуры).

Минусы и недоработки:

1. Сумма скоростей системы не равна нулю, возможно проблема в генераторе случайных чисел.

2. Не удалось воспроизвести правильное давление (и его температурную зависимость), возможно решается подбором коэффициента между энтальпией и энергией фотона.

3. Формула (7) выведена исключительно из математических соображений и имеет слабое физическое обоснование.

4. Непонятно, откуда берется начальное распределение фотонов по энергиям, здесь оно просто постулируется на основании формулы Планка, а должно получатся «естественным образом».

 

Ну и напоследок, вот как выглядят 40’000 атомов: