Резюме – Принципы OFDM модуляции уже получили большое распространение в аппаратуре связи (к сожалению, в основном зарубежного производства). Они обещают высокую спектральную эффективность и в то же время обладают способностью бороться с частотной селективностью каналов. К сожалению, пик-фактор в таких системах больше, чем в системах с одноканальной модуляцией. Теоретические предпосылки для решения задачи снижения пик-фактора рассматриваются в данной статье. В частности, рассматривается связь пик-фактора элементарного OFDM сигнала с начальным распределением фаз на поднесущих. Мы планируем, что эта статья откроет цикл исследований, посвященный вопросам практической реализации принципов OFDM модуляции. .
Введение
В современных электронных словарях дается следующий перевод аббревиатуры:
OFDM (Orthogonal Frequency Division Multiplexing) мультиплексирование с ортогональным частотным разделением сигналов, канал OFDM схема модуляции и тип физического канала для высокоскоростной передачи данных.
В иностранной литературе OFDM упоминается как модуляция или техника или даже как концепция построения приемо-передатчиков. Здесь мы приведем следующую цитату из издания Wireless Communications от 2003 года:
Orthogonal frequency division multiplexing (OFDM) is emerging as the preferred modulation scheme in modern high data rate wireless communication systems. OFDM has been adopted in the European digital audio and video broadcast radio system and is being investigated for broadband indoor wireless communications. Standards such as HIPERLAN2 (High Performance Local Area Network) and IEEE 802.11a and IEEE 802.11g have emerged to support IP-based services.
«Communication\ICI\Пособие.pdf»
Эта цитата передает тот большой интерес к этому направлению за рубежом, который существует несмотря на уже имеющееся широкое внедрение этой техники на практике в виде стандартов и оборудования, которое работает по этим стандартам. Этот интерес в свою очередь связан с большим спектром возможностей, которые предоставляет этот вид модуляции.
К сожалению, автору не известно (не удалось найти информации) о каких-либо успехах в практической реализации этой техники в России. Мы располагаем лишь достаточно разрозненным набором статей, которые рассматривают те или иные аспекты и технические параметры этого вида модуляции без относительно к какой-либо практической реализации.
Эта статья ставит целью открыть рассмотрение именно практических аспектов реализации техники OFDM и будет посвящена параметрам необходимым для эффективной работы радиопередатчиков, усилителей, а именно снижению пик фактора излучаемого OFDM сигнала и соответственно снижения требований к оборудованию по динамическому диапазону мощности излучения.
Как известно пик-фактор (ПФ или peak-to-average power ratio (PAR)) определяется как отношение максимальной (пиковой) мгновенной мощности сигнала к его средней мощности. Например, когда сигнал представлен N отсчетами СN={cn} своей комплексной огибающей на интервале Т, ПФ определяется по формуле:
ПФ = (Max CN) ^ 2 / E CN
Где E CN – усредненная энергия на интервале Т (дисперсия) сигнала
Как известно увеличение этого параметра негативно сказывается на сложности конструкции высокочастотного тракта от усилителей до антенны, ведет к снижению КПД высокочастотного оборудования, ведет к увеличению нелинейных искажений.
Как в зарубежной, так и в отечественной литературе по OFDM модуляции много написано о проблеме ПФ OFDM сигналов. И здесь, чтобы определиться с постановкой задачи, мы должны сначала рассмотреть структуру OFDM сигнала.
СТРУКТУРА OFDM сигнала.
Следует сразу отметить, что структура OFDM сигнала может быть очень сложной поскольку складывается из множества компонент. Перечислим основные из них:
1. структура частотно временного деления: по сетке частот заданная начальной частотой, шагом сетки частот, количеством поднесущих, по временным слотам заданная длительностью символа, длительностью защитного интервала
2. вид манипуляции: фазовая простая, фазовая дифференциальная, смешанная фазовая-амплитудная…
3. вид символьной синхронизаци.
4.наличие и вид избыточного кодирования
5.наличие и вид перемежения данных
В первую очередь мы должны сформулировать и решить задачу получения минимального ПФ самого простого (элементарного) OFDM сигнала без манипуляции, с тем, чтобы затем определить методы влияния фазовой (например) манипуляции на полученную аналитику и учесть это влияние в результатах решения для более сложных задач.
Сравнение OFDM модуляции с другими видами модуляции
Следует обратить особое внимание, что метод OFDM модуляции принципиально отличается от ранее известных традиционных типов модуляции, например, амплитудной или фазовой. Отличие состоит в том, что традиционные методы модуляции применяются во временной области, а метод OFDM модуляции применяется в частотной области.
Это приводит к тому, что и сам модулирующий сигнал определяется в частотной области рис.1. Параметрами сигнала являются шаг сетки частот Fc, первая или нижняя частота в сетке поднесущих Fн , верхняя частота в сетке поднесущих Fв. Соответственно заданные Fc, Fн, Fв определяют количество поднесущих N = (Fв – Fн) / Fс.

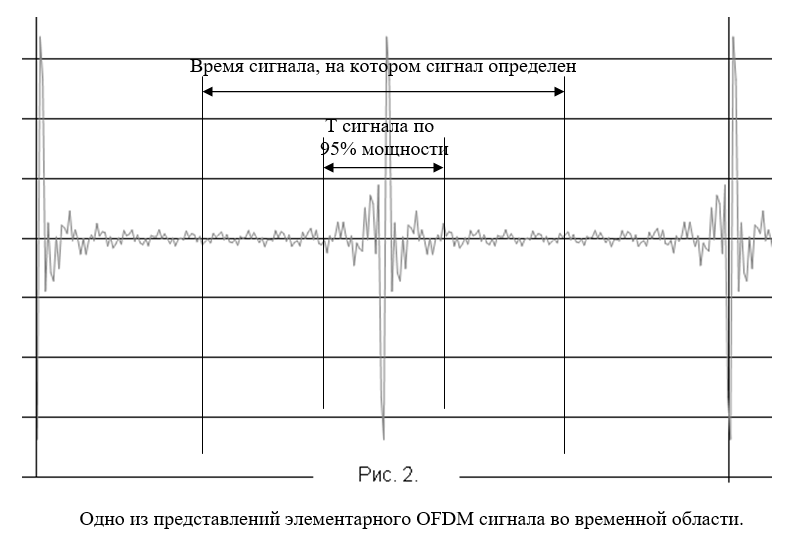
Как известно для представления сигнала в частотной области существует, вообще говоря, неограниченное множество представлений сигнала во временной области, одну из которых мы легко получим с помощью обратного преобразования Фурье от приведенного спектра Рис.2. (ниже).
По приведенному графику без всяких расчетов видно значительное превышение максимального значения сигнала над средним уровнем сигнала, а значит можно сделать вывод о неприемлемом значении параметра Пик-Фактор для данного сигнала.
Для численной оценки этого значения достаточно воспользоваться тем фактом, что обратное преобразование Фурье в данном случае вырождается в простую сумму N гармоник.
И поскольку ПФ одной гармоники равен:
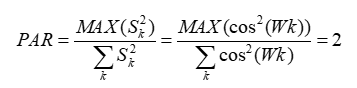
Или в децибелах:
PAR = 10 log 2 = 3 дб
Максимальный ПФ суммы N гармоник равен:
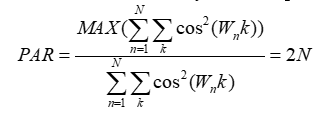
Формулировка и решение задачи поиска сигнала с минимальным ПФ
Выше уже было высказано предположение о том, что ПФ сигнала, который задан отсчетами АЧХ можно снизить с помощью выбора ФЧХ, то есть мы должны найти связь закона изменения фазы в частотной области с законом распределения энергии сигнала во времени. На первый взгляд задача не имеет аналитического решения. Но на самом деле постановка задачи в такой формулировке просто не корректна, потому что получение такой связи или зависимости формы ФЧХ от ПФ является промежуточной задачей, после решения которой нужно было бы искать методы определения минимума относительно ПФ на этой зависимости.
На самом деле, если более четко сформулировать требования к искомому сигналу задача формулируется достаточно четко и решается достаточно просто. Вот эти требования, их всего два:
1.У сигнала должен быть прямоугольный амплитудный спектр (или близкий к прямоугольному)
2. Сигнал должен иметь постоянную амплитуду во времени
Задача состоит в том, что нужно найти сигнал во временной области, который подходит под эти требования, соответственно с помощью преобразования Фурье такого сигнала мы получим прямоугольный амплитудный спектр (поскольку сигнал должен соответствовать требованиям) и искомую фазовую характеристику.
Сигнал, который удовлетворяет обоим этим требованиям уже давно известен – это сигнал с линейным изменением частоты от времени, известный также как сигнал с линейной частотной модуляцией или ЛЧМ сигнал рис.3.
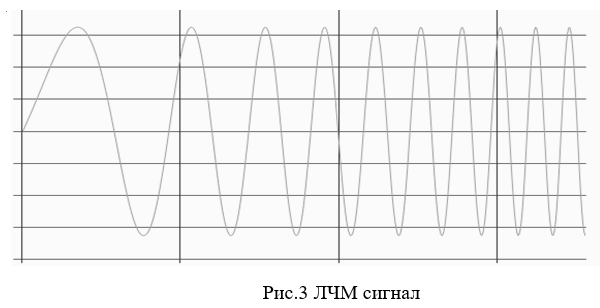

Фазовая характеристика такого сигнала определяется формулой [1]:
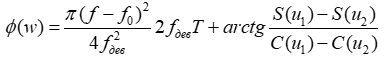
Где S(u) и С(u) интегралы Френеля.
При достаточно больших Т второе слагаемое в этой формуле стремится к постоянной величине pi / 4 и может быть опущено. Таким образом, если ЛЧМ сигнал определен на достаточно большом периоде Т форма его АЧХ приближается к прямоугольной [1] как и требуется, а фазовая характеристика принимает вид квадратичной параболы [1]: .
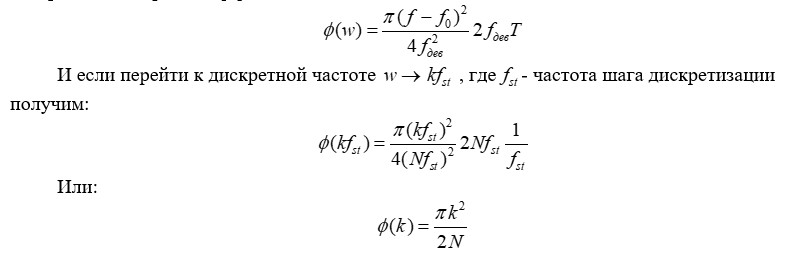
Графики распределения фаз для разного количества гармоник N составляющих OFDM сигнал приведены на рис. 5
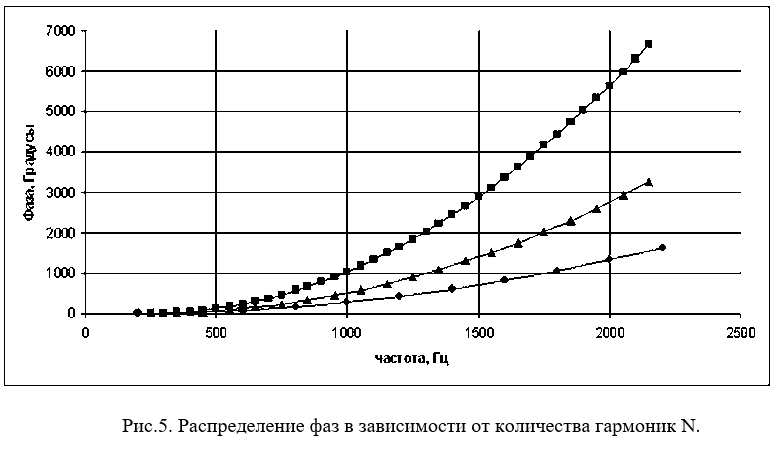
Моделирование суммы 39 гармоник со значениями начальных фаз рассчитанными по закону квадратичной параболы рис.4.подтверждают верность этого решения.
Можно классифицировать такой метод получения дискретной фазовой характеристики как аппроксимацию исходного идеального сигнала (в данном случае ЛЧМ сигнала) дискретными комплексными отсчетами в частотной области.
Рассчитанный на модели ПФ такого 39 тонового сигнала равен 3,18 сравните с максимальным, который равен: PAR = 39 * 2 = 78 и с минимальным: PAR = 2, который определен для одиночного гармонического колебания.
Можно предположить, что с ростом числа гармоник N это значение будет снижаться так как точность аппроксимации будет возрастать.
Строгое математическое доказательство оптимальности полученного метода минимизации ПФ OFDM сигнала (или любого полигармонического сигнала) выходит за рамки указанной статьи.
Постановка задачи минимизации ПФ по набору кодов фазовой манипуляции
Выше мы вывели формулу распределения фаз для элементарного OFDM сигнала. Для передачи информации необходимо выполнять манипуляцию, например фазы поднесущих.
В самом простом случае двухпозиционной манипуляции мы можем рассматривать тот же сигнал как сигнал манипулированный всеми нулями или всеми единицами, то есть данные манипуляции выглядят следующим образом:
0000 0000 0000 0000 0000 0000 0000 0000 0000 000…
1-бит 1х8 2х8 3х8 4х8 39-бит
1111 1111 1111 1111 1111 1111 1111 1111 1111 111…
1-бит 1х8 2х8 3х8 4х8 39-бит

Таким образом, битовое слово или код фазовой манипуляции определяет 2 в степени М реализаций, огибающей информационного сигнала каждая из которых характеризуется собственным значением пик-фактора. Выше мы показали, что квадратичное распределение фазы обеспечивает минимальное значение пик-фактора сигнала во времени. Очевидно, что введение манипуляции фазы относительно этого начального распределения будет ухудшать этот параметр.
Решение задачи минимизации ПФ и/или выработка практических рекомендаций по его снижению на таком наборе реализаций манипулированного сигнала должно будет стать результатом нашего следующего исследовани.
А пока отметим, что для анализа ПФ при М < 20 созданная нами математическая модель позволяет прямой расчет пик-фактора по всем реализациям. На среднем компьютере расчет 50 000 комбинаций занимает не более часа к тому же вычисления легко распараллеливаются.
Значит, следующий этап исследований может быть посвящен структурированию и исследованию результатов моделирования по набору реализаций сигналов с манипулированной огибающей.
Литература
[1] Гоноровский И.С. Радиотехнические цепи и сигналы, 1971 г.
[2] MIL-STD-188-110A HF

