Данная статья продолжает изложение новых методов решения задач математики и физики, не поддававшихся решению в течении столетий.
Введение
В настоящее время Википедия считает, что на сегодня достоверно известно существование четырёх фундаментальных взаимодействий:
гравитационного;
электромагнитного;
сильного;
слабого
Разложение .
О первых двух временных фундаментальных взаимодействиях мы говорили в предыдущей статье. Теперь рассмотрим пространственные фундаментальные взаимодействия (ПРФ).
Для иллюстрации и её остатки приведены на рисунках (откройте изображения правым кликом).
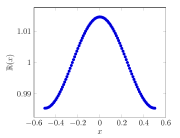
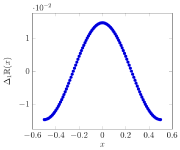


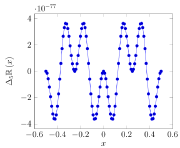
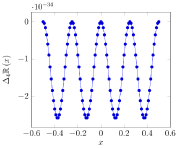
Исходя из выявленных при вычитании функциях, аппроксимация ПРФ имеет следующий вид:
где — нормировочный множитель равный значению суммы в точке максимума.
Как оказалось ПРФ полностью пересматривает фундаментальные понятия взаимодействий. Важнейшую роль в этом сыграла формула Дирака:
где и
— заряды магнитного монополя Дирака,
— заряд электрона и
— заряд позитрона.
Из неё следует, что единичный член в разложении соответствует магнитному монополю. Таким образом, придуманного Х. Юкавой «сильного взаимодействия» не существует.
Далее идёт обычное магнитное взаимодействие. Однако, не всё так просто как раньше.
Взаимодействия пропорциональные
Мы привыкли думать, что квантовая физика возникла в начале прошлого века. Нет, её создал ещё Джеймс Клерк Максвелл.
Это видно из аппроксимаций ПРФ и ВРФ. В каждой из них есть члены, которые пропорциональны , т.е. »линейны» по ПТС! Таким образом, ПТС для уравнений Максвелла была изначально просто нормировочным множителем. В результате уравнения Максвелла одинаковы как в классической физике, так и в квантовой. Или проще говоря, изначально квантовые. Соответственно, их не надо с чем-либо объединять. А вот к ним можно что-либо квантовое добавлять. Хотя их физическая суть в квантовой физике существенно иная, что следует из разделения фундаментальных взаимодействий на пространственные и временные.
Ток смещения
Решётчатая модель пространства-времени позволяет выделить два члена в разложениях и
:
и
Учитывая, что
то существует двукратное различие в величине коэффициентов при и
.
Поэтому член пропорциональный можно сопоставить с утверждением Максвелла, что ток смещения
и изменение электрической индукции
порождают вихревое магнитное поле
:
Таким образом, ток смещения появляется в разложении ПРФ автоматически!
Тогда член пропорциональный можно сопоставить с утверждением Максвелла, что изменение магнитной индукции
порождает вихревое электрическое поле
:
Фотон
В априорной теории всего фотон является локальным возбуждением КиММ.
Достаточно правильным классическим образом фотона является брошенная параллельно поверхности воды плоская морская галька. Периодически касаясь поверхности воды, галька делает отскок и летит дальше.
Поэтому вначале Максвелл и использовал представление об эфире как о среде, от которой галька может оттолкнуться. Дело в том, что уже тогда было очевидно, что, во-первых, ввиду замкнутости магнитных силовых линий они не могут уходить от своего источника. Во-вторых, что оттолкнуться упруго, не теряя энергии, можно только от чего-то существенно более прочного и бесконечно массивного.
Поэтому классическое волновое представление фотона в принципе было неправильно, поскольку в таком случае фотон становился бесконечным по длине. Квантовая механика вместо одиночной волны стала использовать пакет волн, хоть в какой-то степени позволяющий рассматривать фотон как частицу.
Априорная теория всего объясняет квантовую природу электромагнитных волн несколько иначе. Известно, что заряд при ускорении излучает фотоны. Т.е., передаёт энергию кристаллу из магнитных монополей (КиММ). Заметьте, не отдельному монополю, а их мириадам, вблизи которых проходит ускоренно движущийся заряд. Такого рода понятие, названное »фонон», было введено в теорию твёрдого тела советским учёным И. Е. Таммом.
Конкретно в КиММ фотон приобретает два отражения как в южных, так и в северных монополях. Эти отражённые волны можно рассматривать как »опережающую волну из будущего» и »запаздывающую из прошлого». В результате их суперпозиции и получается короткий фотон.
Гипотеза об образовании КиММ
Дело в том, что, как утверждают философы, материя обладает свойством отражения.
Способность ощущения есть всеобщее свойство материи или продукт её организованности.
— Дени Дидро Разговор Д’Аламбера и Дидро // Дидро Д. Сочинения: в 2-х т. Т. 1. — М.: Мысль, 1986. — С. 387.
Это означает, что если появилась изначально некая материя, она тут же это свойство отражения должна и продемонстрировать. Естественно, что возникает чисто диалектический вопрос: что является зеркалом?
Например, если появилась некая электрическая плотность , то где-то и когда-то в будущем должно будет возникнуть и противоположное её отражение. Таким образом, свойство отражения порождает пространство и время как абстракцию отражения.
Математики заменяют пространство и время термином система координат. Физики заменяют пространство и время квантовыми реперными точками. Так как точка является нуль-мерным объектом, то правильно называть её выколотой дыркой в чём-то со знаком!
Такая же ситуация имеет место и для так называемой силы Лоренца, которая может быть выведена из уравнений Максвелла, но понимается как следующее эмпирическое утверждение:
Плотность силы »’
»’, действующая на стационарную плотность заряда »
»’ в данной точке и момент времени и нестационарную плотность тока »
»’, может быть параметризована ровно двумя векторами »
»’ и »’
»’:
Теперь пора вернуться к гипотезе кристалла из магнитных монополей. Свойство отражения порождает ток. Электрическая часть силы Лоренца — это закон Кулона. Поэтому по мере сближения разноимённых компонент тока скорость их сближения будет увеличиваться. Соответственно, чем больше ток, тем сильнее возникающее вокруг него магнитное поле. Однако, учитывая, что процесс идёт при температуре абсолютного нуля, магнитное поле не может проникнуть в объём тока, но может его сжать. Причём это сжатие производится »квантованным воздействием» силы Лоренца. Таким образом, сами магнитные монополи оказываются квантованными.
В результате оба реперных заряда »бронируются» снаружи тонкими слоями монополя, образуя два диона (сумма монополя и электрического реперного заряда) и останавливая процесс сближения исходных компонент. В результате квантования обычный ток становится током смещения по Максвеллу! Таким образом, сверхпроводимость есть следствие квантования тока смещения. Ибо с момента образования монополя его сверхпроводимость сохранится даже при звёздных температурах среды.’
Сверхпроводник ведёт себя формально как идеальный диамагнетик. Однако он не является диамагнетиком, так как внутри него намагниченность равна нулю.
Дальнейшее развитие процесса приводит к образованию КиММ, »плавающего» в реперном пространстве дырок. Следует отметить, что переместиться в реперное пространство дырок вне Вселенных нельзя. Ибо перестраиваемая граница КиММ — это вечный двигатель, создающий дефекты в самом кристалле путём утилизации всего, что достигает границы КиММ изнутри.
При этом, как и полагается в квантовой механике, поверхность магнитных монополей будет колебаться, создавая проходы для всевозможных дефектов КиММ.
Итак, в результате добавления вмороженного слоя диаметр монополя слегка увеличивается и затапливает слой интерференционного электрослабого взаимодействия. Ток смещения, введённый Дж. К. Максвеллом при построении теории электромагнитного поля, теперь появляется автоматически как переменный ток, создающий магнитные монополи.
На самом же деле ток смещения течёт везде, создавая кристалл из магнитных монополей.
Основные дефекты кристалла из магнитных монополей
Продолжение следует…


