Не без участия таланта или атлетизма этих людей, но совершенство находится в глазах смотрящего. Для чисел совершенство же определяется математически. «Совершенные числа» равны сумме своих собственных делителей (делители — положительные целые числа, отличные от рассматриваемого числа, которые делят его без остатка). Например, 6 = 3 + 2 + 1, а 28 = 14 + 7 + 4 + 2 + 1. Хотя эти математические диковины могут так же украшать стены Лувра, как и выполнять сальто назад с поворотом, но тем не менее они действительно являют собой нечто уникальное: совершенную тайну.

Евклид изложил основы совершенных чисел более 2000 лет назад. Он знал, что первыми четырьмя совершенными числами были 6, 28, 496 и 8128. С тех пор было обнаружено гораздо больше совершенных чисел. Но, как ни странно, все они чётные. Никто не смог найти совершенное нечетное число, и после многих тысяч лет безуспешных поисков может возникнуть соблазн сделать вывод, что нечетных совершенных чисел не существует. Но и математики этого доказать не смогли. Как же так выходит, что мы можем так много знать о четных совершенных числах и в то же время не можем ответить на самый простой вопрос о нечетных? И как современные математики пытаются решить этот древний вопрос?
Наше исследование математического совершенства начинается с делителей. Мы знаем, что 6 является делителем 12, поскольку 12/6 = 2, и мы знаем, что 25 является делителем 100, поскольку 100/25 = 4. Как мы уже говорили, мы знаем, что число является совершенным, когда оно равно сумме своих собственных делителей — тех делителей, которые меньше самого числа. Мы также можем назвать число совершенным, если сумма всех его делителей, собственных и несобственных, вдвое больше числа. Это работает, потому что единственный несобственный делитель числа — это само число. Мы видим, что число 28 также является совершенным по этому определению: его собственные делители — 1, 2, 4, 7 и 14, его несобственный делитель — 28, а сумма всех его делителей — 1 + 2 + 4 + 7 + 14 + 28, равна 56, что представляет собой 2 × 28. Включение несобственного делителя в сумму удобно для некоторых элементов алгебры, которые мы будем использовать чуть позже с совершенными числами.
При работе с совершенными числами мы часто употребляем определение «сумма делителей числа», поэтому математики упростили задачу, превратив это значение в функцию. Мы определим σ(n), или «сигму числа n», как сумму делителей числа n. Мы уже знаем, что σ(28) = 56. Еще несколько примеров: σ(1) = 1, σ(6) = 1 + 2 + 3 + 6 = 12 и σ(10) = 1 + 2 + 5 + 10 = 18. Обратите внимание, что 6 — совершенное число, поскольку σ(6) = 2 × 6, а 1 и 10 — нет. Как мы видим, эта функция σ обладает некоторыми особыми свойствами, которые идеально подходят для изучения совершенных чисел.
Итак, у нас есть базовое определение совершенных чисел и новый математический инструмент, который поможет нам их найти. С чего начать поиски? Мы начнем с того, с чего математики всегда начинают изучать числа и их закономерности: с простых чисел.
Простое число по определению делится только само на себя и на 1. Это упрощает вычисление σ для простого числа: σ(2) = 1 + 2 = 3, σ(3) = 1 + 3 = 4, σ(5) = 1 + 5 = 6 и σ(7) = 1 + 7 = 8. В общем, для любого простого числа p, σ(p) = 1 + p.
Может ли простое число быть совершенным? Только если σ(p) = 1 + p = 2p. Немного алгебры нам в помощь, и мы видим, что это тождество верно всякий раз, когда p = 1, но поскольку простые числа больше 1 по определению, ни одно простое число не может быть совершенным. Итак, мы знаем, что простые числа не могут быть совершенными. Что дальше?
Степень простых чисел, таких как 24, 53 или 1136, — хороший следующий шаг, так как их делители легко организовать. Рассмотрим степень простого числа, например, 16, или 24. Единственными делителями 24 являются степени от 2 до 24: 20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16. Таким образом, σ(24) может вычисляться следующим образом:
σ(24) = 1 + 2 + 22 + 23 + 24 = 1 + 2 + 4 + 8 + 16 = 31.
Если обобщить, для любой степени простого числа pn: σ(pn) = 1 + p + p2 + p3 + … + pn.
Станет еще проще, если мы воспользуемся формулой с урока алгебры. Обратите внимание, что каждый из добавляемых членов в σ(pn) в p раз больше предыдущего члена. Получается так называемый ряд геометрической прогрессии, и вот хорошая формула для суммы ряда:
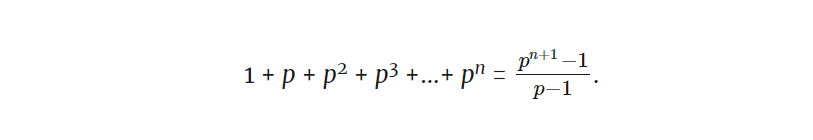
Подробнее об этой удивительной формуле в упражнениях в конце статьи.
Благодаря формуле ряда геометрической прогрессии, нам не нужно перечислять все делители числа pn для вычисления σ(pn). Мы можем просто использовать формулу:
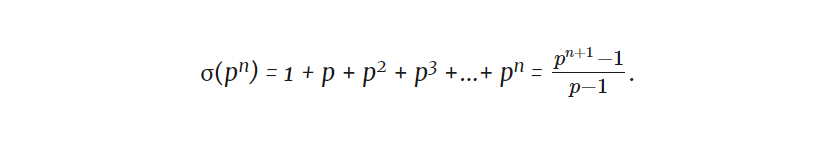
Например, мы уже видели, что
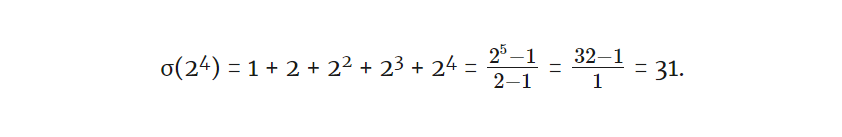
И мы можем вычислить сумму делителей других простых степеней, просто подставив их в формулу:
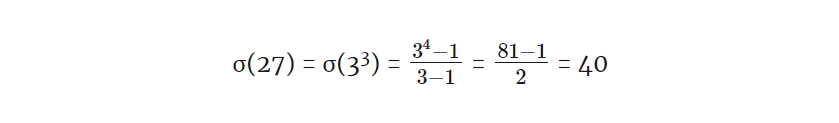
и

Обратите внимание, что ни одна из этих степеней простых чисел не удовлетворяет условию совершенности σ(24) ≠ 2 × 24, σ(33) ≠ 2 × 33, and σ(112) ≠ 2 × 112. Фактически, никакая степень простого числа не может быть совершенной. Чтобы получить совершенное число, нам нужно σ(pn) = 2pn, что будет означать: 1 + p + p2 + p3 + … + pn-1 + pn = 2pn.
Мы можем вычесть pn из обеих частей уравнения и получить: 1 + p + p2 + p3 + … + pn-1 = pn.
Теперь воспользуемся формулой ряда геометрической прогрессии в левой части этого уравнения и получим:

Необходимо, чтобы это было верно, чтобы pn был совершенным. Но обратите внимание, что pn — 1 меньше, чем pn, и деление pn — 1 на p — 1 сделает его еще меньше, поэтому:
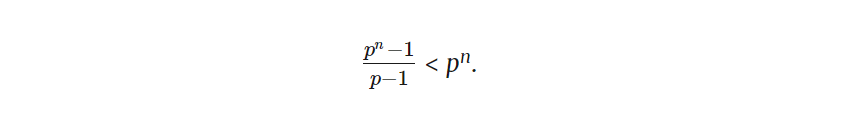
Таким образом, никакая простая степень pn не может быть совершенной.
Итак, нет совершенных простых чисел и нет совершенных простых степеней. Что может быть совершенным? Что ж, мы знаем, что 28 — совершенное число, и это произведение двух различных степеней простых чисел: 28 = 22 × 7.
Любое число, не являющееся простым числом или степенью простого числа, может быть записано как произведение различных степеней простого числа, подобного этому. И эти факторизации вместе с особым свойством функции σ могут помочь нам определить, является ли число совершенным.
Мы уже знаем, что σ(28) = 1 + 2 + 4 + 7 + 14 + 28, но давайте подробнее рассмотрим эту сумму. Обратите внимание, что каждое из последних трех чисел кратно 7:

Мы можем вынести это число 7, чтобы выявить некую скрытую структуру: σ(28) = (1 + 2 + 4) + 7 × (1 + 2 + 4).
И с помощью более умного разложения на множители (факторизации) с распределительным свойством мы можем написать: σ(28) = (1 + 2 + 4)(1 + 7).
Это не говорит нам о том, чего мы раньше не знали: σ(28) = (1 + 2 + 4)(1 + 7) = 7 × 8 = 56, что подтверждает, что 28 является совершенным числом. Но внутри этого умножения скрывается кое-что важное: σ(28)=(1+2+4)(1+7)=(1+21+22)(1+71).
Выражения в скобках кажутся знакомыми: 1 + 21 + 22 = σ(22) и 1 + 71 = σ(7). Это означает, что мы действительно можем написать: σ(28) = σ(22)σ(7).
Чтобы вычислить σ(28) = σ (22 × 7), мы можем фактически вычислить σ(22) и σ(7) и умножить их. Это удивительно, и, в целом, верно: каждый раз, когда вы выполняете разложение числа на простые числа, как это, вы можете использовать эту комбинацию для вычисления σ. Например, поскольку 100 = 22 × 52, мы можем вычислить σ(100) следующим образом:
σ(100) = σ(22)σ(52) = (1 + 2 + 4)(1 + 5 + 25) = 7 × 31 = 217, что немного проще, чем перечислить все девять делителей 100 и сложить их.
Почему это работает? Что сказать, делители числа происходят от его простых делителей. Снова рассмотрите число 28, которое является произведением 22 и 7, и подумайте о таблице умножения ниже:
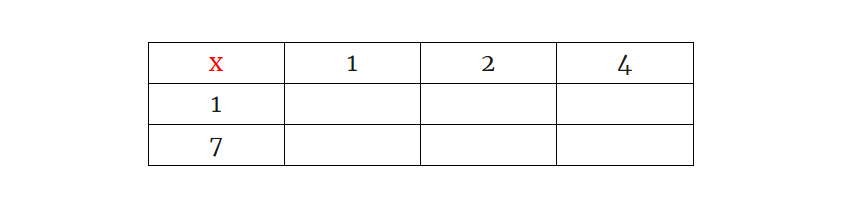
По горизонтали указаны степени числа 2, которые нацело делят 28, а по вертикали — степени 7, которые нацело делят 28. Обратите внимание, что происходит, когда мы заполняем эту таблицу умножения.
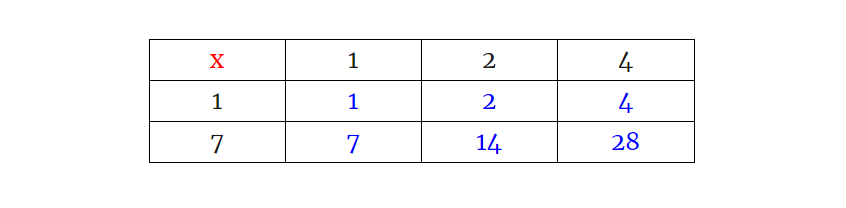
Мы получаем все делители 28. Это потому, что каждый делитель 28 представляет собой комбинацию делителей 22 и 7, степеней простых чисел, которые появляются при факторизации 28.
Теперь сравните таблицу умножения с выражением: (1 + 2 + 4) (1 + 7).
Когда мы умножаем с помощью свойства распределения, это также дает все делители 28, а затем складывает их: (1 + 2 + 4)(1 + 7) = 1 × 1 + 2 × 1 + 4 × 1 + 7 × 1 + 7 × 2 + 7 × 4.
Другими словами, (1 + 2 + 4) (1 + 7) в точности равно σ(28). Но (1 + 2 + 4)(1 + 7) также является σ(22)σ(7). Итак, σ(22)σ(7) = σ(28). Этот пример демонстрирует очень полезный факт о σ: на языке теории чисел эта функция является «мультипликативной». Это означает, что σ (ab) = σ(a)σ(b), если числа a и b «взаимно просты», то есть у них нет общих делителей.
Это особенность σ, которая помогает нам изучать совершенные числа. Евклид использовал этот факт 2000 лет назад, чтобы создать формулу для нахождения совершенных чисел с помощью особого вида простых чисел и умных аргументов в отношении произведений и делителей. При этом он сделал первый шаг к определению того, как должно выглядеть каждое четное совершенное число. Посмотрим, как он это сделал.
Во-первых, обратите внимание, что для любой степени двойки мы имеем
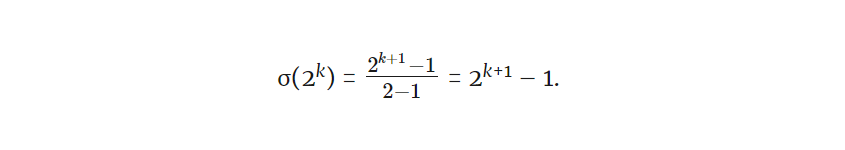
Это следствие формулы ряда геометрической прогрессии, которую мы обсуждали ранее. Теперь рассмотрим следующий мысленный эксперимент: что, если 2k+1 — 1 простое число?
Итак, поскольку σ(p) = 1 + p для любого простого числа, мы знаем, что σ(2k+1 – 1) = 1 + 2k+1 – 1 = 2k+1. И обратите внимание, что 2k+1 ровно вдвое больше 2k из-за закона экспонент, который гласит, что 2 × 2k = 2k+1. Итак, у нас есть следующие два интересных отношения между числами 2k и 2k+1 — 1:
σ(2k) = 2k+1 – 1 и σ(2k+1 – 1) = 2k+1 = 2 × 2k.
Евклид заметил хитрый способ использовать эти отношения: он перемножил два числа вместе, чтобы получилось число M = 2k × (2k+1 — 1), и пока (2k+1 — 1) — простое число, это число совершенно! Чтобы убедиться в этом, вычислим σ(M) и покажем, что оно равно 2M.
Во-первых, обратите внимание, что 2k+1 — 1 на единицу меньше четного числа, поэтому оно должно быть нечетным. Это означает, что 2k+1 — 1 не делится на 2. Но 2k делится только на степень 2. Таким образом, 2k и 2k+1 — 1 не имеют общих делителей и поэтому взаимно просты. Это позволяет нам использовать мультипликативное свойство σ:
σ(M) = σ (2k ×(2k+1 – 1)) = σ (2k) σ (2k+1 – 1).
Мы уже знаем, что σ(2k) = 2k+1 – 1 и σ(2k+1 – 1) = 2k+1 = 2 × 2k, поэтому мы можем найти σ(M):
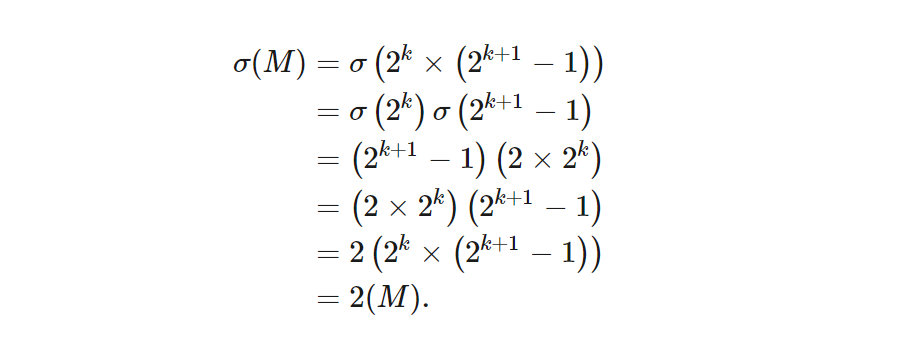
Итак, M= 2k ×(2k+1 – 1), как утверждается, совершенно.
Имейте в виду, что это основано на предположении, что число 2k+1 — 1 простое. Эти числа называются простыми числами Мерсенна, и вы, возможно, слышали о них в связи с широкомасштабным проектом добровольных вычислений по поиску простых чисел Мерсенна (GIMPS), совместной онлайн-вычислительной попытки найти огромные простые числа Мерсенна. Каждый раз, когда вы слышите об открытии нового наибольшего простого числа, это, вероятно, результат работы GIMPS. И, благодаря доказательству Евклида, каждый раз, когда открывается новое простое число Мерсенна, также открывается новое совершенное число.
Например, 25 – 1 = 31 это простое число Мерсенна, и, таким образом, 24(25-1) = 16 × 31 = 496 является совершенным числом. Также, 22 – 1 = 3 это простое число Мерсенна, и, таким образом, 21(22 – 1) = 2 × 3 = 6 является совершенным числом. И 23 – 1 = 7 это простое число Мерсенна, и, таким образом 22(23 – 1) = 4 × 7 = 28 является совершенным числом.
Вы могли заметить, что все эти совершенные числа четные. Это имеет смысл, потому что, пока k > 0, число 2k × (2k+1 — 1) будет четным. (И если k = 0, то 2k+1 — 1 равно 1, что не является простым числом).
Возможно, вы также заметили, что все совершенные числа, которые мы обсуждали до сих пор, похоже, связаны с простыми числами Мерсенна. Это не случайно: через 2000 лет после того, как Евклид показал, что эта формула порождает совершенные числа, Леонард Эйлер доказал, что это единственный способ получить четные совершенные числа. Но вопрос о том, какими могут быть нечетные совершенные числа (если они существуют), оставался открытым.
И он остается открытым сегодня. Хотя математики не могут найти такие числа, у них есть много информации о том, как может выглядеть гипотетическое нечетное совершенное число. Оно не может делиться на 105; должно иметь как минимум девять различных простых делителей, второй по величине из которых должен быть больше 10 000. И оно должно иметь остаток 1 при делении на 12 или остаток 9 при делении на 36.
Может показаться странным доказывать результаты о числах, которых может даже не существовать. Но каждое новое правило еще больше сужает поиск. И если математикам повезет, они могут просто доказать, что нечетные совершенные числа должны удовлетворять двум несовместимым критериям, что раз и навсегда докажет, что нечетных совершенных чисел не существует.
В поисках несовместимых критериев математики даже начали искать не совсем совершенные числа. «Поддельное совершенное число» — это число, которое выглядит как совершенное, если вы притворитесь, что один из его непростых делителей на самом деле является простым. Например, 60, произведение 3, 4 и 5, можно считать «поддельным совершенным числом»: если представить, что 4 в его факторизации — простое число, тогда комбинации, которые мы разработали для σ, дадут нам: (1+3)(1+4)(1+5) = 4 × 5 × 6 = 120.
Если бы σ(60) равнялось 120, то 60 было бы совершенным. Конечно, σ(60) на самом деле не равно 120, но похоже, что это так, если мы представим, что 4 — простое число. Вот что делает его «поддельным».
Эти «подделки» похожи на обобщения совершенных чисел, и поэтому все, что верно в отношении «подделки», должно быть правдой и в отношении совершенного числа. Понятие нечетных «подделок» было бы особенно полезно, поскольку любое правило, обнаруженное для нечетных «подделок», можно было бы добавить к существующим правилам для нечетных совершенных чисел, увеличивая шансы на обнаружение противоречивых критериев и сужая общее пространство поиска.
Рене Декарт, еще один известный математик, вовлеченный в тайну совершенных чисел, открыл первое «поддельное» нечетное совершенное число и призвал математиков найти другие. Приняв вызов, математики расширили понятие «подделки» и открыли новый класс чисел для изучения. По большей части исследования этих «подделок» совершенных чисел проводятся просто ради удовольствия от математических изысканий. Но, возможно, что-то, что мы узнаем о «подделках», поможет нам доказать, что на самом деле нечетные совершенные числа не могут существовать, или же наоборот.
Может показаться странным тратить тысячи лет на поиск чисел с любопытными свойствами, доказывая теоремы об объектах, которые могут даже не существовать, и изобретать новые и даже более странные миры чисел для исследования. Но для математика это имеет совершенный смысл.
Упражнения
- Число называется «избыточным», если оно меньше суммы его собственных делителей. Например, 36 — это избыточное число, поскольку 1 + 2 + 3 + 4 + 6 + 9 + 12 + 18 = 55, что больше 36. Назовите наименьшее избыточное число.
- Число считается «недостаточным», если оно больше суммы собственных делителей. Например, 35 является недостаточным, поскольку 1 + 5 + 7 = 13, что меньше 35. Являются ли простые степени недостаточными или избыточными?
- Используйте свойство дистрибутивности, чтобы умножить (p — 1)(1 + p + p2 + p3 +… + pn) и упростить.
- Предположим, что N — нечетное число, и предположим, что M = 2N и является совершенным. Покажите, что N должно быть равно 3.
Ответы
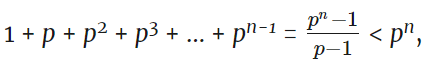
это приводит к дефициту степеней простых чисел. Конечно, простые числа являются неполноценными, поскольку сумма собственных делителей простого числа всегда равна 1. Обратите внимание, что это доказывает, что существует бесконечно много недостаточных чисел.
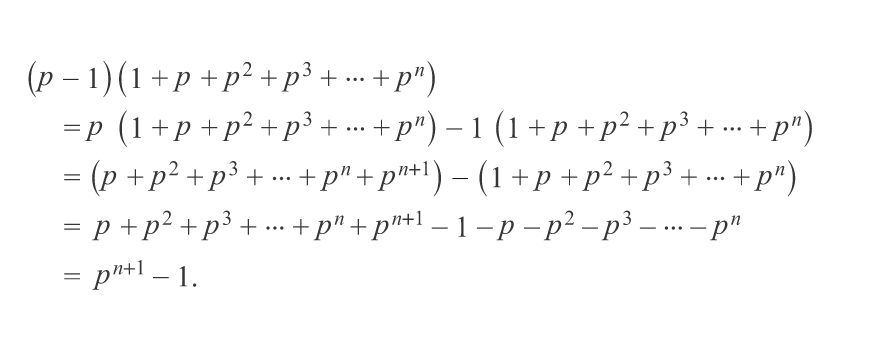
Обратите внимание, что, поскольку (p – 1) (1 + p + p2 + p3 + … + pn )= pn+1 — 1, мы можем разделить обе части уравнения на p — 1, чтобы получить:
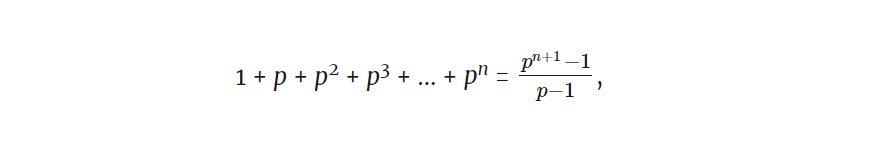
формулу суммы ряда.
Поскольку обе части этого уравнения являются целыми числами и 3 не делит 4, 3 должно делить N. Таким образом, мы можем написать:
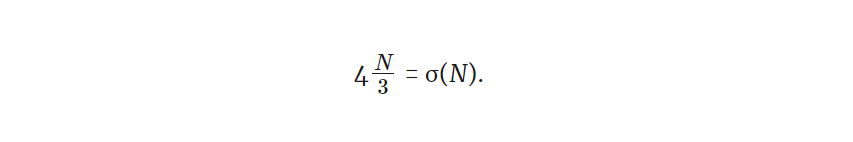
Поскольку N/3 должно быть целым числом, оно также является делителем N. N также является делителем N, поэтому мы знаем, что сумма делителей N равна по крайней мере сумме этих двух. То есть,
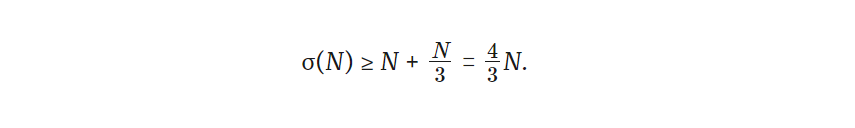
Но мы уже знаем, что σ(N) = 4/3 * N. Если бы у N было больше делителей, σ(N) было бы больше 4/3 * N, поэтому 3 должно быть его единственным делителем. Таким образом, N = 3, как заявлено.
Это конкретное применение доказательства Эйлера того, что каждое четное совершенное число имеет вид M = 2k × (2k+1 — 1), где 2k+1 — 1 является простым числом Мерсенна.

