Снижение объёма выборки экспериментальных данных без потери информации

В чем проблема гистограмм экспериментальных данных

Основой управления качеством продукции любого промышленного предприятия является сбор экспериментальных данных с последующей их обработкой.

Первичная обработка результатов эксперимента включает сопоставление гипотез о законе распределения данных, описывающем с наименьшей погрешностью случайную величину по наблюдаемой выборке.

Для этого выборка представляется в виде гистограммы, состоящей из $$ столбцов, построенных на интервалах протяженностью $$.

Идентификации формы распределения результатов измерений требует также ряд задач, эффективность решения которых отличается для различных распределений (например, использование метода наименьших квадратов или вычисление оценок энтропии).

Кроме того, идентификация распределения нужна ещё и потому, что рассеяние всех оценок (среднеквадратичного отклонения, эксцесса, контрэксцесса и др.) также зависит от формы закона распределения.

От объема выборки зависит успешность идентификации формы распределения экспериментальных данных и, если он мал, особенности распределения оказываются замаскированными случайностью самой выборки. На практике обеспечить большой объем выборки, например больше 1000, не представляется возможным в силу разных причин.

В такой ситуации важно наилучшим образом распределить выборочные данные по интервалам, когда для дальнейшего анализа и расчетов интервальный ряд необходим.

Следовательно, для успешной идентификации нужно решать вопрос о назначении числа интервалов k

А. Хальд в книге [1] пространно убеждает, что существует оптимальное число интервалов группирования, когда ступенчатая огибающая гистограммы, построенной на этих интервалах, наиболее близка к плавной кривой распределения генеральной совокупности.

Одним из практических признаков приближения к оптимуму может служить исчезновение в гистограмме провалов, и тогда близким к оптимуму считается наибольшее k, при котором гистограмма еще сохраняет плавный характер.

Очевидно, что вид гистограммы зависит от построения интервалов принадлежности случайной величины, однако, даже в случае равномерного разбиения удовлетворительного способа такого построения до сих пор нет.

Разбиение, которое можно было бы считать правильным, приводит к тому, что ошибка аппроксимации кусочно-постоянной функцией предположительно непрерывной плотности распределения (гистограммой) будет минимальной.

Затруднения вызваны тем, что оцениваемая плотность неизвестна, поэтому число интервалов сильно сказывается на виде распределения частот конечной выборки.

При фиксированной длине выборки укрупнение интервалов разбиения ведет не только к уточнению эмпирической вероятности попадания в них, но и к неизбежной потере информации (как в общем смысле, так и в смысле кривой распределения плотности вероятности), поэтому при дальнейшем необоснованном укрупнении изучаемое распределение слишком сильно сглаживается.

Однажды возникнув, задача оптимального разбиения размаха под гистограмму не исчезает из поля зрения специалистов, и пока не появится единственное устоявшееся мнение относительно ее решения, задача будет оставаться актуальной.

Выбор критерия оценки качества гистограммы экспериментальных данных

Критерий Пирсона, как известно, требует разбиения выборки на интервалы — именно в них производится оценка отличия между принятой моделью и сравниваемой выборкой.

где:$$ — экспериментальные значения частот $$;$$– значения частот в том же столбце;m-число столбцов гистограммы.

Однако применение этого критерия в случае интервалов постоянной длины, используемых обычно для построения гистограмм, неэффективно. Поэтому в работах по эффективности критерия Пирсона рассматриваются интервалы не с равной длиной, а с равной вероятностью в соответствии с принимаемой моделью.

При этом, однако, число интервалов равной длины и число интервалов равной вероятности различаются в разы (за исключением равновероятного распределения), что позволяет сомневаться в достоверности полученных в [2] результатов.

В качестве критерия близости целесообразно использовать энтропийный коэффициент, который вычисляется так [3]:

где:$$— число наблюдений в i-м интервале $$

Алгоритм оценки качества гистограммы экспериментальных данных с применением энтропийного коэффициента и модуля numpy.histogram

Синтаксис использования модуля следующий [4]:

numpy.histogram(a,bins=m, range=None, normed=None, weights=None, density=None)

Будем рассматривать методы поиска оптимального числа m интервалов разбиения гистограммы реализованных в модуле numpy.histogram:

• ‘auto’ — максимум оценок ‘sturges’ и ‘fd’, обеспечивает хорошую производительность;
• ‘fd’ (Freedman Diaconis Estimator) — надежный (устойчивый к выбросам) оценщик, который учитывает изменчивость и размер данных;
• ‘doane’ — улучшенная версия оценки sturges, которая точнее работает с наборами данных с распределением, отличным от нормального;
• ‘scott’ — менее надежный оценщик, который учитывает изменчивость и размер данных;
• ‘stone’ — оценщик основан на перекрестной проверке оценки квадрата ошибки, можно рассматривать как обобщение правила Скотта;
• ‘rice’ — оценщик не учитывает изменчивость, а только размер данных, зачастую переоценивает количество необходимого числа интервалов;
• ‘sturges’ — метод (по умолчанию), учитывающий только размер данных, оптимален только для гауссовых данных и недооценивает количество интервалов для больших негауссовых наборов данных;
• ‘sqrt’ — оценщик квадратного корня из размера данных, используемый Excel и другими программами для быстрых и простых расчётов количества интервалов.

Чтобы начать описание алгоритма, адаптируем модуль numpy.histogram() для расчёта энтропийного коэффициента и энтропийной погрешности:

from numpy import* def diagram(a,m,n):          z=histogram(a, bins=m)         if type(m) is str:#перевод текстового имени оценщика в числовое значение                 m=len(z[0])             y=z[0]                 d=z[1][1]-z[1][0]#оценка интервала разбиения         h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#энтропийная погрешность         ke=h/std (a)#энтропийный коэффициент  по соотношению (1).               return ke,h

Теперь рассмотрим основные этапы алгоритма:

1) Формируем контрольную выборку (далее «большую выборку» ), отвечающую требованиям к погрешности обработки экспериментальных данных. Из большой выборки путем удаления всех нечетных членов сформируем меньшую выборку (далее «малую выборку» );

2) Для всех оценщиков ‘auto’,’fd’,’doane’,’scott’,’stone’,’rice’,’sturges’,’sqrt’ вычисляем энтропийный коэффициент ke1 и погрешность h1 по большой выборке и энтропийный коэффициент ke2 и погрешность h2 по малой выборке, а также абсолютное значение разности — abs(ke1-ke2);

3) Контролируя численные значения оценщиков на уровне не менее четырёх интервалов, выбираем оценщик, обеспечивающий минимальное значение абсолютной разности — abs(ke1-ke2).

4) Для окончательного решения выбора оценщика строим на одной гистограмме распределения для большой и малой выборки при оценщике, обеспечивающем минимальное значение abs(ke1-ke2), а на второй при оценщике, обеспечивающем максимальное значение abs(ke1-ke2). Появление дополнительных скачков в малой выборке на второй гистограмме подтверждает правильность выбора оценщика на первой.

Рассмотрим работу предложенного алгоритма на выборке данных из публикации [2]. Данные были получены случайным отбором 80 заготовок из 500 с последующим измерением их массы. Заготовка должна иметь массу в следующих пределах: $$кг. Оптимальные параметры гистограммы определим, используя следующий листинг:

import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n):          z=histogram(a, bins=m)         if type(m) is str:#перевод текстового оценщика в числовое значение                 m=len(z[0])             y=z[0]                 d=z[1][1]-z[1][0]#оценка интервала разбиения         h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#абсолютная энтропийная погрешность         ke=h/std (a)#энтропийный коэффициент                 return ke,h  a =array([17.37, 17.06, 16.96, 16.83, 17.34, 17.45, 17.60, 17.30, 17.02, 16.73, 17.08, 17.28, 17.08, 17.21, 17.29,17.47, 16.84, 17.39, 16.95, 16.92, 17.59, 17.28, 17.31, 17.25, 17.43,17.30, 17.18, 17.26, 17.19, 17.09,16.61, 17.16, 17.17, 17.06, 17.09,16.83, 17.17, 17.06, 17.59, 17.37,17.09, 16.94, 16.76, 16.98, 16.70, 17.27, 17.48, 17.21, 16.74, 17.12,17.33, 17.15, 17.56, 17.45, 17.49,16.94, 17.28, 17.09, 17.39, 17.05, 16.97, 17.16, 17.38, 17.23, 16.87,16.84, 16.94, 16.90, 17.27, 16.93,17.25, 16.85, 17.41, 17.37, 17.50,17.13, 17.16, 17.05, 16.68, 17.56 ] )  c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a)   b=[a[i] for i in arange(0,len(a),1) if not  i%2 == 0] n1=len(b)  print("Среднее квадратичное отклонение  для выборки (n=80) : %s"%round(std(a),3)) print("Математическое ожидание для выборки (n=80):%s"%round(mean(a),3)) print("Среднее квадратичное отклонение для выборки (n=40):    %s"%round(std(b),3)) print("Математическое ожидание выборки (n=40):  %s"%round(mean(b),3)) u=[]  for m in c:               ke1,h1=diagram(a,m,n)         ke2,h2=diagram(b,m,n1)         u.append(abs(ke1-ke2))         print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m))  u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))]  plt.title('Оптимальный оценщик: %s n для минимальной разности abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show()  plt.title('Не оптимальный оценщик: %s n для максимальной разности abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show() 

Получим:

Среднее квадратичное отклонение для выборки (n=80):0.24
Математическое ожидание для выборки (n=80): 17.158
Среднее квадратичное отклонение для выборки (n=40):0.202
Математическое ожидание выборки (n=40): 17.138
ke1=1.95,h1=0.467,ke2=1.917,h2=0.387,dke=0.033,m=auto
ke1=1.918,h1=0.46,ke2=1.91,h2=0.386,dke=0.008,m=fd
ke1=1.831,h1=0.439,ke2=1.917,h2=0.387,dke=0.086,m=doane
ke1=1.918,h1=0.46,ke2=1.91,h2=0.386,dke=0.008,m=scott
ke1=1.898,h1=0.455,ke2=1.934,h2=0.39,dke=0.036,m=stone
ke1=1.831,h1=0.439,ke2=1.917,h2=0.387,dke=0.086,m=rice
ke1=1.95,h1=0.467,ke2=1.917,h2=0.387,dke=0.033,m=sturges
ke1=1.831,h1=0.439,ke2=1.917,h2=0.387,dke=0.086,m=sqrt

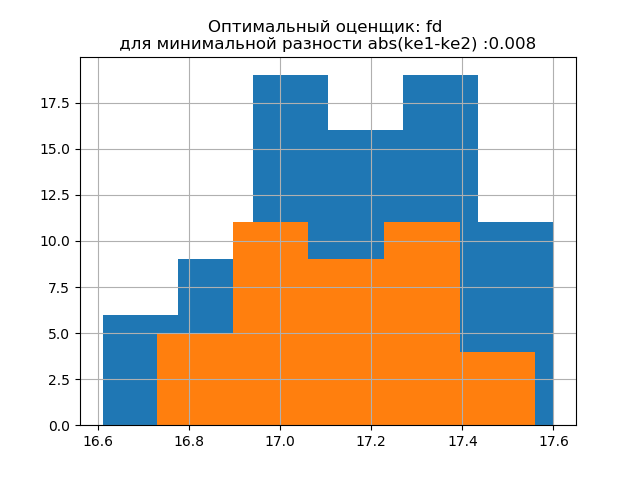
Форма распределения большой выборки подобна форме распределения малой выборки. Как и следует из писания ‘fd’ — надежный (устойчивый к выбросам) оценщик, который учитывает изменчивость и размер данных. При этом энтропийная погрешность малой выборки даже немного уменьшается: h1=0,46, h2=0,386 при незначительном уменьшении энтропийного коэффициента от k1=1,918 до k2=1,91.

Формы распределения большой и малой выборки различаются. Как следует из описания, ‘doane’ — улучшенная версия оценки ‘sturges’, которая лучше работает с наборами данных с распределением, отличным от нормального. В обеих выборках энтропийный коэффициент близок к двум, а распределение близко к нормальному.Появление дополнительных скачков в малой выборке на на этой гистограмме, по сравнению с предыдущей, дополнительно свидетельствует о правильном выборе оценщика ‘fd’.

Генерируем новые две выборки для нормального распределения с параметрами mu=20,sigma=0.5 и size=100 с использованием соотношения:

a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)])

К полученной выборке применим разработанный метод, используя следующую программу:

import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n):          z=histogram(a, bins=m)         if type(m) is str:#перевод текстового оценщика в числовое значение                 m=len(z[0])             y=z[0]                 d=z[1][1]-z[1][0]#оценка интервала разбиения         h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#абсолютная энтропийная погрешность         ke=h/std (a)#энтропийный коэффициент                 return ke,h #a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) a=array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945,20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a)   b=[a[i] for i in arange(0,len(a),1) if not  i%2 == 0] n1=len(b) print("Среднее квадратичное отклонение  для выборки (n=80):%s"%round(std(a),3)) print("Математическое ожидание для выборки (n=80):%s"%round(mean(a),3)) print("Среднее квадратичное отклонение для выборки (n=40):%s"%round(std(b),3)) print("Математическое ожидание выборки (n=40): %s"%round(mean(b),3)) u=[] for m in c:               ke1,h1=diagram(a,m,n)         ke2,h2=diagram(b,m,n1)         u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title('Оптимальный оценщик: %s n для минимальной разности abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('Не оптимальный оценщик: %s n для максимальной разности abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show() 

Получим:
Среднее квадратичное отклонение для выборки (n=80):0.524
Математическое ожидание для выборки (n=80):19.992
Среднее квадратичное отклонение для выборки (n=40):0.462
Математическое ожидание выборки (n=40): 20.002
ke1=1.979, h1=1.037,ke2=2.004,h2=0.926,dke=0.025,m=auto
ke1=1.979,h1=1.037,ke2=1.915,h2=0.885,dke=0.064,m=fd
ke1=1.979, h1=1.037,ke2=1.804,h2=0.834,dke=0.175,m=doane
ke1=1.943, h1=1.018,ke2=1.934,h2=0.894,dke=0.009,m=scott
ke1=1.943, h1=1.018,ke2=1.804,h2=0.834,dke=0.139,m=stone
ke1=1.946, h1=1.02,ke2=1.804,h2=0.834,dke=0.142,m=rice
ke1=1.979,h1=1.037,ke2=2.004,h2=0.926,dke=0.025,m=sturges
ke1=1.946,h1=1.02,ke2=1.804,h2=0.834,dke=0.142,m=sqrt

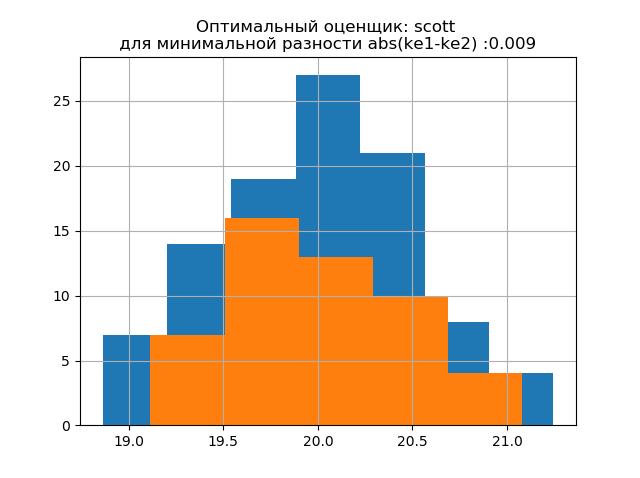
Форма распределения большой выборки подобна форме распределения малой выборки. Как и следует из описания, ‘scott’ – менее надежный оценщик, учитывающий изменчивость и размер данных. При этом энтропийная погрешность малой выборки даже немного уменьшается: h1=1,018 а h2=0,894 при незначительном уменьшении энтропийного коэффициента от k1=1,943 до k2=1,934.. Следует отметить что для новой выборки мы получили ту же тенденцию изменения параметров что и в предыдущем примере.

Формы распределения большой и малой выборки различаются. Как следует из описания, ‘doane’ — улучшенная версия оценки ‘sturges’, которая точнее работает с наборами данных с распределением, отличным от нормального. В обеих выборках распределение является нормальным. Появление дополнительных скачков в малой выборке на на этой гистограмме по сравнению с предыдущей дополнительно свидетельствует о правильном выборе оценщика ‘scott’.

Применение сглаживания для сравнительного анализа гистограмм

Сглаживание гистограмм, построенных по большой и малой выборке позволяет более точно определить их идентичность с точки зрения сохранения информации, содержащейся в выборке большего объёма. Представим последние две гистограммы в виде функций сглаживания:

from numpy import* from scipy.interpolate import UnivariateSpline from matplotlib import pyplot as plt a =array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945, 20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) b=[a[i] for i in arange(0,len(a),1) if not  i%2 == 0] plt.title('Сглаживание выборок с минимальной n разностью abs(ke1-ke2)' ,size=12) z=histogram(a, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='Большая выборка n=100') z=histogram(b, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='Малая выборка n=50') plt.legend(loc='best') plt.grid() plt.show() plt.title('Сглаживание выборок с максимальной n разностью abs(ke1-ke2)' ,size=12) z=histogram(a, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='Большая выборка n=100') z=histogram(b, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='Малая выборка n=50') plt.legend(loc='best') plt.grid() plt.show()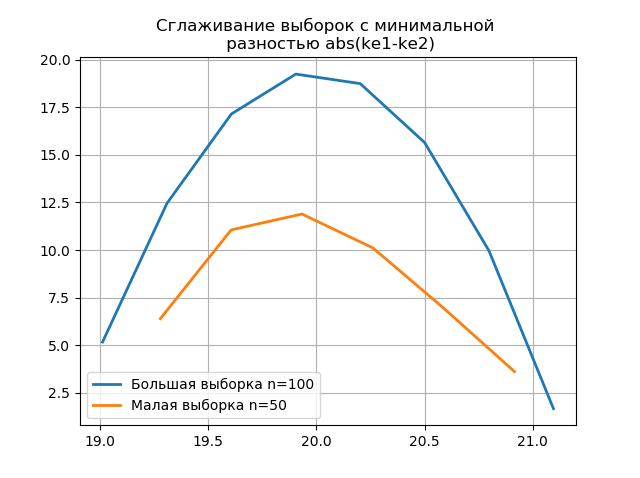

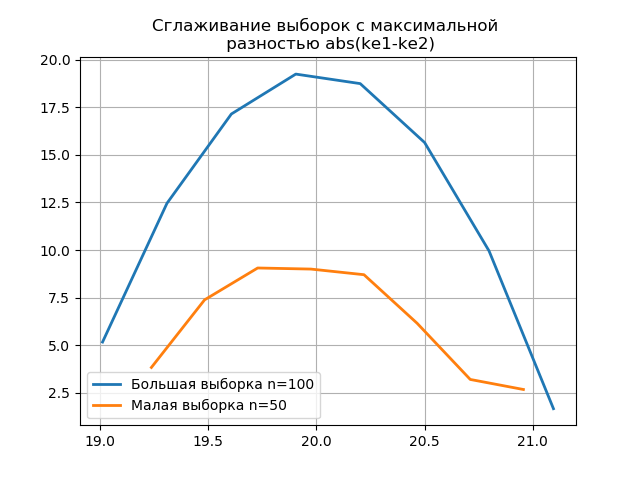
Появление дополнительных скачков в малой выборке на графике сглаженной гистограммы по сравнению с предыдущим дополнительно свидетельствует о правильном выборе оценщика ‘scott’.

Выводы

Приведённые в статье вычисления в диапазоне распространенных на производстве малых выборок, подтвердили эффективность использования энтропийного коэффициента как критерия сохранения информативности выборки при уменьшении её объёма. Рассмотрена методика применения последней версии модуля numpy.histogram с встроенными оценщиками — ‘auto’, ‘fd’, ‘doane’, ‘scott’, ‘stone’, ‘rice’, ‘sturges’, ‘sqrt’, которых вполне достаточно для оптимизации анализа экспериментальных данных по интервальным оценкам.

Ссылки:

1. Хальд А. Математическая статистика с технически¬ми приложениями. — Москва: Изд-воиностр. лит., 1956
2. Калмыков В. В., Антонюк Ф. И., Зенкин Н. В.
Определение оптимального количества классов группирования экспериментальных данных при интервальных оценках // Южносибирский научный вестник.— 2014.— №3.—С. 56—58.
3. Новицкий П. В. Понятие энтропийного значения погрешности // Измерительная техника .—1966.— № 7.—С. 11—14.
4. numpy.histogram — NumPy v1.16 Manual