Шум в компьютерной томографии: насколько он действительно мешает нам?

15.06.2023

Здравствуй, Хабр! На связи отдел компьютерной томографии Smart Engines.

Как уже, наверное, известно нашему читателю, мы занимаемся разработкой томографического программного обеспечения. Мы работаем над совершенствованием алгоритмов реконструкции внутренней структуры объектов, боремся с артефактами реконструкции и различного рода шумами в измеренных данных. Наша основная задача — повысить качество реконструкции, увидеть чуть больше и чуть четче то, что когда-то было недоступно человеческому глазу.

Каждый пиксель детектора «живет своей жизнью и ошибается по своему». Ошибки связаны с шумом, который в каждом пикселе распределен уникальным образом и часто зависит от самого зарегистрированного значения. Такой шум называют гетероскедастичным.

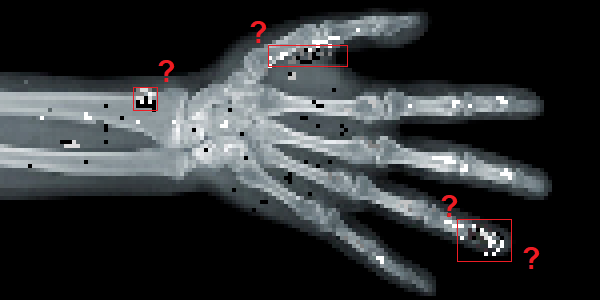
Гетероскедастичность порождает на восстановленных изображениях искажения, которые мешают правильной интерпретации получаемых результатов. Наш отдел имеет опыт в противостоянии подобным зашумленностям данных, и сегодня мы хотели бы рассказать о придуманном нами методе фильтрации гетероскедастичного шума [1].

Пример гетероскедастичного шума. Красными прямоугольниками обозначены области с пикселями, значения в которых сомнительны: можно ли доверять этим значениям.

Напомним, что компьютерная томография — неразрушающий метод восстановления внутренней морфологической структуры объектов по набору зарегистрированных под разными углами проекций. Объект зондируется рентгеновским излучением, которое при прохождении через него ослабляется. Ослабленное излучение регистрируется позиционно-чувствительным детектором. При помощи алгоритмов реконструкции в применении к полученным на детекторе рентгеновским снимкам объекта (проекциям) осуществляется восстановление внутренней морфологии объекта. В реальности все несколько сложнее — есть много препятствий на этом пути!

В измеренных проекционных данных присутствуют шумы, которые искажают реконструированное изображение и в, конечном итоге, могут привести к неверным выводам исследователя. Нередко шум на проекционных снимках характеризуется тем, что дисперсия ошибки значения регистрируемого сигнала (количество рентгеновских квантов) зависит от математического ожидания сигнала в этом пикселе, и поэтому дисперсии ошибок значений сигнала в различных пикселях неодинаковы и могут сильно различаться от пикселя к пикселю. Абсолютные значения регистрируемых значений сигнала в соседних пикселях в такой ситуации могут отличаться на несколько порядков. Описанный шум на проекционных данных называется гетероскедастичным шумом.

Причины присутствия гетероскедастичного шума разнообразны. Он может быть обусловлен существенной неоднородностью объекта и наличием сильно поглощающих включений, содержащихся в объекте. Причина может скрываться в сбое работы регистрирующего оборудования, шум может быть обусловлен необходимостью сильного ограничения дозовой нагрузки. Гетероскедастичность наблюдается, когда время регистрации одной проекции (время экспозиции) мало.

Так или иначе проявление гетероскедастичности тесно связано с природой процесса регистрации рентгеновских квантов каждым отдельным пикселем детектора, на обсуждении чего мы временно и остановимся. В компьютерной томографии при зондировании монохроматическим излучением регистрируемое пикселем детектора значение формируется потоком рентгеновских квантов, прошедших через исследуемый объект в направлении “источник-детектор” за определенное время экспозиции, и описывается следующим выражением:

$I_1=I_0 \int e^{-\mu(l)}dl,$

где – число квантов зонда, $\mu$ – линейный коэффициент ослабления рентгеновского излучения используемой длины волны материалом объекта. Процесс регистрации проекционного снимка объекта является стохастическим (случайным) процессом, и случайная величина может быть описана следующей функцией распределения Пуассона с параметром $P(I_1=k)=\frac{\lambda^k e^{-\lambda}}{k!},$

где – вероятность того, что дискретная величина принимает значение . И среднее, и дисперсия распределения величины в такой модели равняются параметру распределения Пуассона $\lambda$ .

Для решения задачи компьютерной томографии, – то есть восстановления пространственного распределения коэффициента $\mu$ , — удобно линеаризовать исходную задачу и перейти к изучению случайной величины $y=\ln I_0 - \ln I_1$ . Поскольку логарифм есть монотонная функция на своей области определения, распределение вероятности линеаризованной дискретной случайной величины не меняется относительно функции распределения вероятностей изначальной величины . Тогда математическое ожидание и дисперсия величины рассчитываются по формулам:

$E=\sum_{i=1}^{\infty} (\ln I_0 - \ln k_i)\frac{\lambda^{k_i} e^{-\lambda}}{k_i!},$ $Var = \sum_{i=1}^{\infty}(\ln I_0 - \ln k_i - E)^2\frac{\lambda^{k_i} e^{-\lambda}}{k_i!},$

где обозначает реализацию случайной величины .

Без ограничения общности описания придуманного нами метода рассмотрим 2D случай реконструкции, то есть будем говорить о реконструкции одного сечения объекта. Модель распространения рентгеновских лучей — параллельная или веерная. В алгебраическом подходе к реконструкции дискретизация соотношения $I_1=I_0 \int e^{- \mu(l)}dl$ и замена интегрирования суммированием позволяет сформулировать задачу компьютерной томографии как задачу решения СЛАУ

— проекционная матрица (прямой оператор проецирования) размера $N \times M$ , $N=n \times n$ — количество пикселей восстанавливаемого объекта , — количество проекционных углов, — оценка линейного коэффициента ослабления, компоненты вектора — линеаризованные значения, зарегистрированные всеми ячейками детектора для всех проекционных углов. Решение СЛАУ в свою очередь может быть заменено решением оптимизационной задачи

$\| Ax-y \|_2 \xrightarrow{\quad x \quad} \min.$

Как модифицировать эту оптимизационную задачу для учета эффекта гетероскедастичности?.

Величины математического ожидания $E=\sum_{i=1}^{\infty}(\ln I_0 - \ln k_i) \frac{\lambda^{k_i}e^{-\lambda}}{k_i!}$ и дисперсии $Var = \sum_{i=1}^{\infty}(\ln I_0 -\ln k_i - E)^2\frac{\lambda^{k_i}e^{-\lambda}}{k_i!}$ линеаризованной случайной величины ввиду быстрой сходимости рядов могут быть достаточно точно оценены частичными суммами этих рядов. К частичным суммам очень близкими оказываются результаты симуляции процесса регистрации сигнала ячейкой детектора методом Монте-Карло. На рис. 1 приведены результаты сравнения значений частичной суммы дисперсии и результатов симуляции методом Монте-Карло. В качестве генератора случайных величин использовался генератор для распределения Пуассона numpy.random.poisson (lam=i, size=5000). Модельные расчеты проводились для значений в интервале $\lambda$ от 30 до 500 с шагом 0.5. Для каждого значения было сгенерировано 5000 значений.

*Рис. 1. Сравнение теоретического результата с результатом моделирования.*

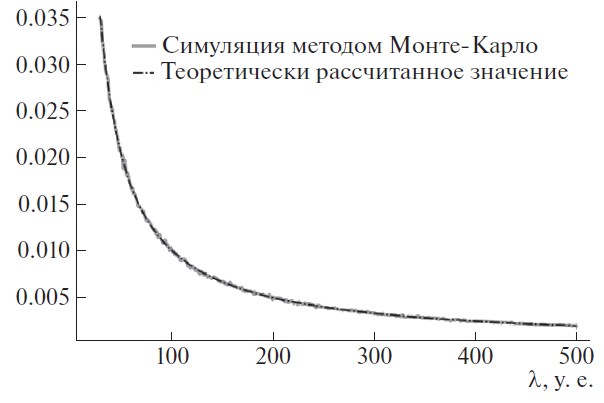
Близость результатов симуляции и теоретических выкладок выступают в пользу корректности расчета дисперсий методом Монте-Карло. Так, имеем способ оценки для каждого пикселя детектора дисперсии значения сигнала, регистрируемого им. Вычисленные оценки дисперсий для всех пикселей могут быть представлены в виде матрицы.

Будучи вычисленными, значения, обратные значениям квадратного корня из дисперсии разных пикселей могут быть использованы в качестве весов для коррекции проекционной матрицы с целью учета свойства гетероскедастичности наблюдений. Таким образом, чем больше дисперсия данных, тем меньше мы доверяем измеренному в этой ячейке детектора значению. При решении задачи реконструкции, припишем вес, равный обратному среднеквадратическому отклонению (корень из дисперсии) каждому наблюдаемому значению сигнала:

$y^*=y \circ \frac{1}{\sqrt{D}},$

здесь $\frac{1}{\sqrt{D}}$ обозначает матрицу, составленную из значений, обратных значениям среднеквадратического отклонения значений сигнала, который зарегистрирован пикселями детектора, $\circ$ — операция поэлементного умножения матриц (произведение Кронекера матриц). Использование веса из обратных значений среднеквадратических отклонений значений сигнала соответствует тому, что пикселю детектора с большим значением дисперсии зарегистрированного сигнала мы “доверяем” меньше, чем пикселю с относительно небольшой дисперсией сигнала (именно поэтому матрица носит название матрицы “доверия”). Тогда исходная СЛАУ перепишется в виде

$\frac{1}{\sqrt{D}} \circ Ax = y^*,$

и оптимизационная задача может быть переформулирована как

$F = \| \frac{1}{\sqrt{D}} \circ Ax - y^* \|_2 \xrightarrow{\quad x \quad}\min.$

Для ее решения мы используем метод наискорейшего спуска. После выписывания в явном виде градиента минимизируемого функционала

$\nabla F = 2A^T \left( \frac{1}{\sqrt{D}} \circ \left[\frac{1}{\sqrt{D}} \circ Ax - y^* \right] \right)$

может быть явно выписан шаг итерации метода:

$x_{k+1}=x_k-\gamma_k \nabla F(x_k),$

где $\gamma_k$ — шаг спуска. Оптимальное значение шага рассчитывается одним из методов решения оптимизационной задачи $\gamma_k=\arg \min_{\gamma} (x_k - \gamma \nabla F(x_k))$ . На этом описание нашего метода учета гетероскедастичности завершено.

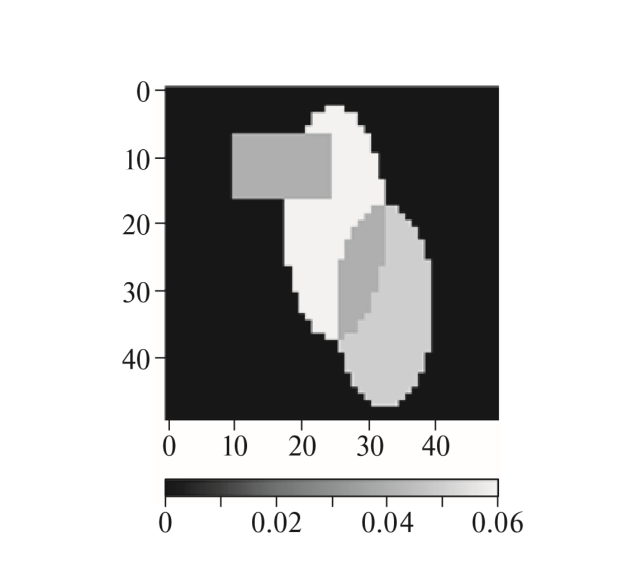
Разработанный метод учета гетероскедастичности был протестирован нами на синтетических данных. Для этого был использован фантом размером 50 × 50 пикселей, изображение которого представлено на рис. 2.

*Рис. 2. Изображение фантома, использованного в экспериментах.*

Были проведены эксперименты, моделирующие различные ситуации, имеющие место на практике в ходе измерения проекционных данных [1]:

время экспозиции (время регистрации одной проекции) различается для первой и второй половины проекционных данных;
сбой отклика детектора случился при одном из проекционных углов;
наличие на проекционных данных шума (к значениям идеальной синограммы добавлен нормально распределенный аддитивный шум);
время регистрации каждой проекции (время экспозиции) одинаково мало.

Результаты всех экспериментов на синтетических данных показывают увеличение точности реконструкции при учете гетероскедастичности. На рис. 3 представлены реконструированные изображения в проведенных экспериментах методом SIRT (а) и предложенным методом с учетом гетероскедастичности (б). Количество итераций метода SIRT в проведенных экспериментах составляет 50-100 итераций. В экспериментах 1 и 2 среднеквадратическое отклонение результата реконструкции от использованного для расчета проекций фантома при реконструкции методом SIRT составило 6.8e-1 (эксперимент 1) и 2.4e-4 (эксперимент 2), при реконструкции описанным методом с учетом гетероскедастичности– 4.4e-6 (эксперимент 1) и 1.6e-6 (эксперимент 2). В экспериментах 3 и 4 также наблюдается уменьшение среднеквадратического отклонения результата реконструкции при учете гетероскедастичности (в пределах одного порядка).

Рис. 3. Результаты реконструкции алгебраическими методами в экспериментах 1-4: а – методом SIRT, б – предлагаемым методом.

Полученные результаты эксперимента 3 при этом демонстрируют высокую чувствительность нового подхода к наличию аддитивного нормально распределенного шума. Это следует учитывать при выборе метода реконструкции, если сбор проекций проведен в нестабильных условиях.

В случае эксперимента 4 с малым временем экспозиции об улучшении качества реконструкции говорит визуально большая однородность фона на изображении, восстановленном с учетом гетероскедастичности (б), чем при использовании метода SIRT для реконструкции (а). Это свойство оказывается важным при применении автоматических методов оценки качества реконструкции, в которых привлечены интегральные метрики сравнения с опорным (идеальным) изображением. Более подробно ознакомиться с описанием и результатами приведенных экспериментов можно в нашей статье [1].

Заключение

Полученные результаты демонстрируют, что учет гетероскедастичности действительно позволяет повысить качество реконструкции. Учет свойства гетероскедастичности шума не нов, однако к нему не перестают апеллировать и сегодня при создании и исследовании различных математических инструментов.

На этом и наши исследования вовсе не заканчиваются — мы планируем в дальнейшем оценить вклад учета гетероскедастичности при решении задачи реконструкции на реальных данных и, может быть, внедрить в наше томографическое программное обеспечение Smart Tomo Engine. Будем держать тебя в курсе, Хабр!

Список литературы

Чукалина М. В. и др. УЧЕТ ГЕТЕРОСКЕДАСТИЧНОСТИ В ИЗМЕРЯЕМЫХ ТОМОГРАФИЧЕСКИХ ПРОЕКЦИЯХ ПРИ РЕАЛИЗАЦИИ АЛГЕБРАИЧЕСКОГО ПОДХОДА В ТОМОГРАФИЧЕСКОЙ РЕКОНСТРУКЦИИ //Сенсорные Системы. – 2022. – Т. 36. – №. 1.

Источник

Шум в компьютерной томографии: насколько он действительно мешает нам?

Читайте также

Паблик ВКонтакте

Последние посты