[Перевод] Спросите Итана: где проходит грань между математикой и физикой?

Симуляции того, как чёрная дыра в центре Млечного Пути может выглядеть для телескопа Event Horizon Telescope. В симуляциях предполагается, что горизонт событий существует, что релятивистские уравнения верны, и что мы используем правильные параметры интересующей нас системы.

Когда речь идёт об описании физического мира, мы можем делать это эпизодически, как это часто бывает, или использовать науку. Последний вариант подразумевает сбор численных данных, поиск корреляций между наблюдениями, формулирование физических законов и теорий, запись уравнений, позволяющих предсказать результаты развития различных ситуаций. Чем более продвинутые физические явления мы описываем, тем более абстрактными и сложными становятся уравнения и теоретические платформы. Но во время формулирования этих теорий и записи уравнений, описывающих, что произойдёт при различных условиях – не перемещаемся ли мы из мира физики в мир математики? Где расположена граница между ними? Именно такой вопрос задаёт наш читатель:

Где провести линию между абстрактной математикой и физикой? Теорема Нётер относится к научному знанию или к математике? А что насчёт теории Малдасены об AdS/CFT-соответствии?

К счастью, чтобы найти различие, нам не обязательно обращаться к таким сложным примерам.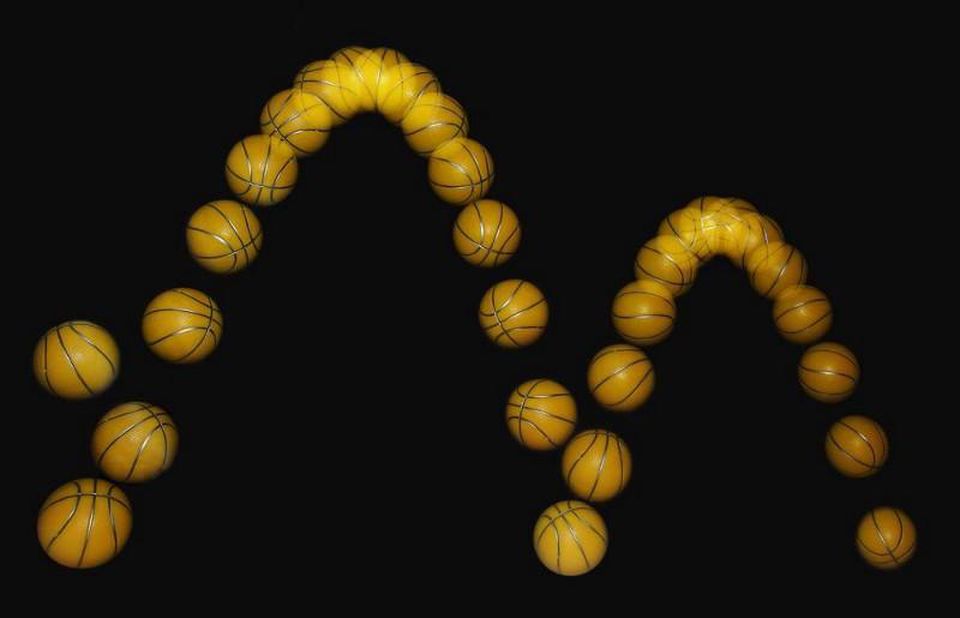


Зная положение и скорость частицы в любой точке траектории, вы сможете рассчитать, где и когда она ударится о землю. Но математически вы получаете два решения, и чтобы выбрать из них правильное, необходимо применить физику.

Допустим, вы выполняете такое простое действие, как бросок мяча. В любой момент времени, если вы скажете мне, где он находится и как движется (положение и скорость), я смогу предсказать, где и когда он ударится о землю. Но вот только если просто записать и решить уравнения, управляемые законами движения Ньютона, не получишь одного правильного ответа. Вместо этого ответов будет два: один соответствующий соударению мяча с землёй в будущем, а другой показывающий, где мяч ударился бы о землю в прошлом. Математика уравнений не сообщает вам, какой из ответов, положительный или отрицательный, корректен физически. Это всё равно, что спросить, чему равен квадратный корень из четырёх: ваш инстинкт говорит «два», но это может быть и минус два. Математика сама по себе не всегда детерминистская.

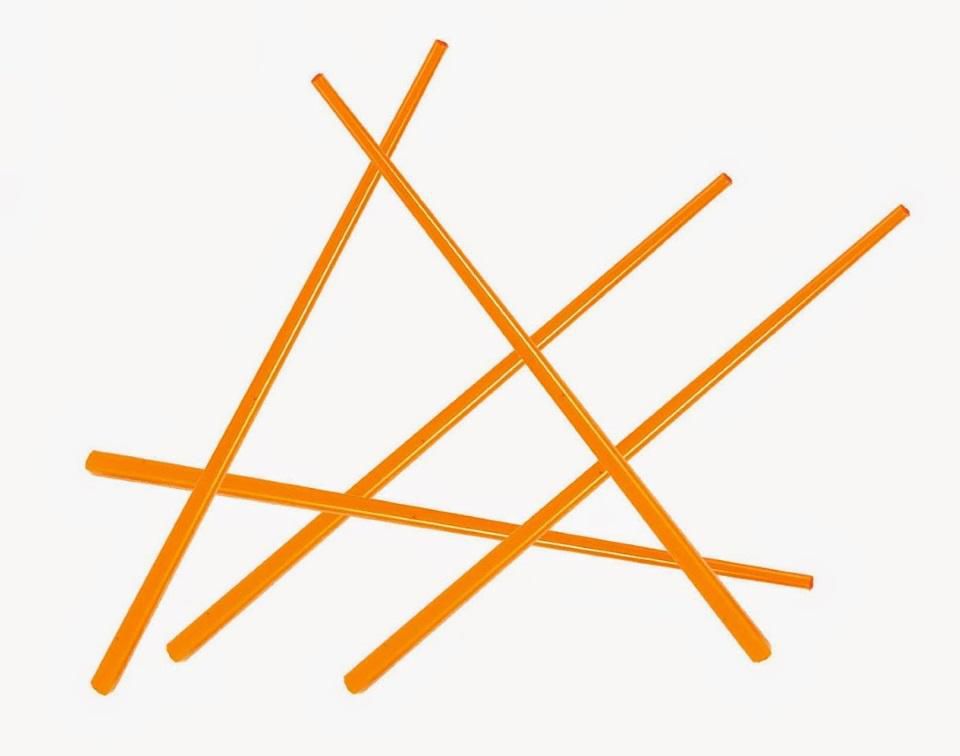
Пять упавших палочек для еды могут сформировать треугольник. Но, как во многих математических задачах, есть вероятность получить больше одного треугольника. Там, где математических решений много, прийти к ответу нам помогает физика

На самом деле, нет никакого универсального правила, которое можно было бы применить, чтобы узнать, какой ответ вам нужен! Именно это и есть наибольшее различие между математикой и физикой: математика сообщает вам все возможные решения, но физика позволяет выбрать решение, описывающее нашу Вселенную.

Пример, конечно, очень упрощённый, и в нём применимо достаточно простое правило: выбери решение, лежащее в будущем времени и в пространстве по ходу движения. Но это правило не получится применить в любой теории, например, в теории относительности и квантовой механике. Когда уравнения оказываются не настолько интуитивными физически, гораздо сложнее узнать, какое из возможных решений будет физически осмысленным.

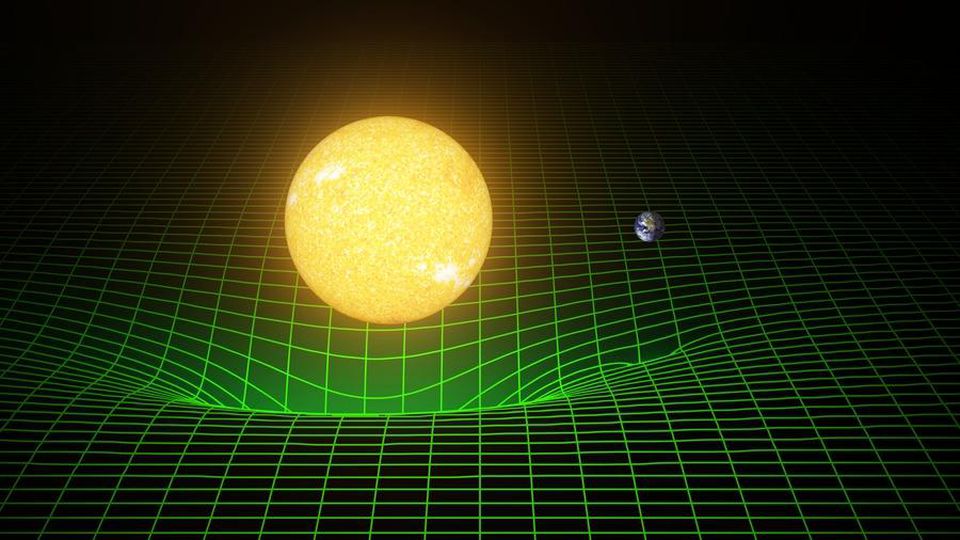
Математика, управляющая Общей теорией относительности, довольно сложна, а сама ОТО предлагает множество возможных решений уравнений. Но, только определяя условий, описывающих нашу Вселенную и сравнивая теоретические предсказания с измерениями и наблюдениями, мы можем получить физическую теорию.

Что же делать, когда математика становится более абстрактной? Что делать, встретившись с ОТО, квантовой теорией поля, или даже ещё более абстрактной и спекулятивной теорией, вроде космической инфляции, дополнительных измерений, теорий великого объединения, теории струн? Математические структуры, создаваемые вами для описания этих возможностей, являются не более чем структурами; сами по себе они не дадут вам физических идей. Но если вы сможете извлечь либо наблюдаемые величины, либо связь с физически наблюдаемыми величинами, то вы начнёте переходить в ту область, которую можно проверить и пронаблюдать.

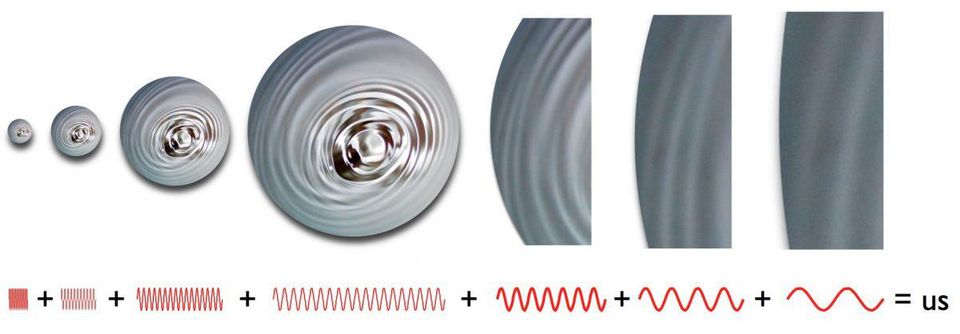
Квантовые флуктуации, происходящие во время инфляции, растягиваются на всю Вселенную, но они же вызывают флуктуации в общей плотности энергии, из-за чего у нас остаётся ненулевая пространственная кривизна Вселенной. Эти флуктуации полей вызывают несовершенства плотностей в ранней Вселенной, что приводит к температурным флуктуациям, которые мы наблюдаем в реликтовом излучении.

К примеру, в инфляционной космологии существует множество сложных уравнений, управляющих всем происходящим. Это очень похоже на математику, и во многих обсуждениях не очень похоже на физику. Но главное тут в том, чтобы объединить предсказания этих математических уравнений с физическими наблюдениями. К примеру, на основе существования квантовых флуктуаций в ткани пространства, и растяжения и расширения пространства с экспоненциальной скоростью во время инфляции, можно ожидать появления ряби и несовершенств в значении квантового поля, вызванных инфляцией по всей Вселенной. По окончанию инфляции эти флуктуации превращаются в флуктуации плотности, которые мы можем увидеть, как флуктуации температуры в остаточном свечении Большого взрыва. Это предсказание 1980-х было подтверждено такими спутниками, как COBE, WMAP и Planck много лет спустя.

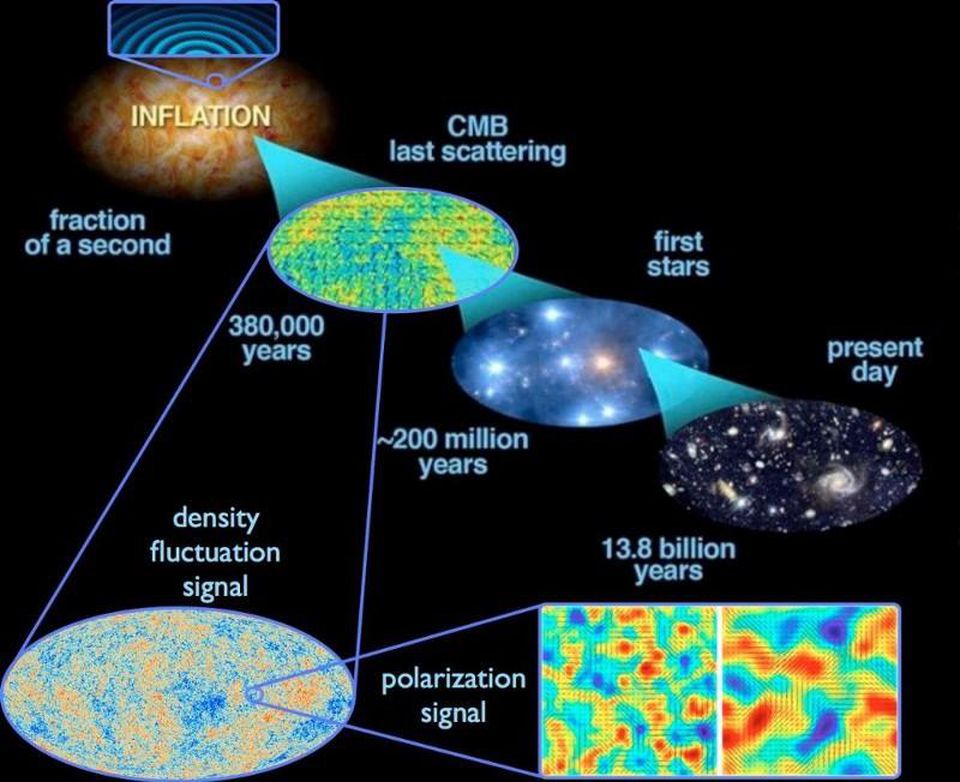
Квантовые флуктуации, происходящие во время инфляции, растягиваются по Вселенной, и когда инфляция заканчивается, они становятся флуктуациями плотности. Со временем это приводит к появлению крупномасштабных структур в сегодняшней Вселенной, а также к флуктуациям температуры, наблюдаемым в реликтовом излучении

Теорема Нётер – интересный пример математической теоремы, имеющей весьма серьёзные математические последствия, а также очень особым образом применимой к физике. В целом теорема говорит о том, что если у вас есть система, интегрирующая лагранжиан, и у системы есть симметрия, то с этой симметрией должна быть связана некоторая сохраняющаяся величина. В физике функция интеграла от лагранжиана соответствует «действию», и поэтому для любой системы, которую можно смоделировать при помощи лагранжиана, и содержащей симметрию, можно вывести некий закон сохранения. В физике это позволяет нам выводить такие вещи, как сохранение энергии, сохранение импульса и сохранение электрического заряда.

Разные системы отсчёта, включающие разные позиции и движение, сталкивались бы с разными законами физики в случае несохранения импульса. То, что у нас есть симметрия преобразования скорости, говорит нам о наличии сохраняющейся величины: линейного импульса.

Что интересно, если бы мы не могли описать Вселенную при помощи математических уравнений, содержащих эти симметрии, то не было бы причин ожидать сохранения этих величин. Поэтому многих людей удивляет то, что в ОТО нет никакой универсальной симметрии по переносу во времени, то есть, для расширяющейся Вселенной, в которой мы обитаем, нет закона сохранения энергии! Отдельные взаимодействия в квантовой теории поля подчиняются такой симметрии, поэтому там энергия сохраняется. Но на масштабе всей Вселенной энергия даже не определена, то есть, мы не знаем, сохраняется она или нет.

Двумерная проекция многообразия Калаби-Яу, одного популярного метода компактификации дополнительных ненужных измерений теории струн. Гипотеза Малдасены состоит в том, что антидеситтеровское пространство математически дуально конформным теориям поля в количестве измерений, меньшем на единицу.

Гипотеза Малдасены ещё более сложная. Она также известна, как AdS/CFT-соответствие, и показывает, что существует математическая дуальность – то есть, подчинение обеих систем одним и тем же уравнениям – между конформной теорией поля (что-то вроде силы в квантовой механике) и теорией струн в антидеситтеровском пространстве с одним дополнительным измерением. Если обеими системами управляют одни и те же уравнения, у них должна быть одна физика. Так что, в принципе, мы должны суметь описать аспекты нашей четырёхмерной (три пространственных и одно временное измерение) Вселенной точно так же, как описывается пятимерное антидеситтеровское пространство-время с правильными параметрами. Это один из ближайших примеров применения голографического принципа ко Вселенной.

Теория струн (или, точнее, теории струн) обладает своими собственными ограничениями, как и взаимодействия Вселенной, поэтому неясно, существует ли взаимно однозначное соответствие между нашей четырёхмерной Вселенной, с гравитацией, электромагнетизмом и ядерными силами, и какой-то из версий теории струн. Гипотеза интересная, и она нашла определённые применения в реальном мире: в изучении кварк-глюонной плазмы. В этом смысле это уже больше, чем математика: это физика. Но где именно она отклоняется от физики в мир чистой математики, пока ещё не совсем ясно.

Лагранжиан Стандартной модели — единое уравнение, включающее частицы и взаимодействия Стандартной модели. У него есть пять независимых частей: глюоны (1), слабые бозоны (2), взаимодействие материи со слабым взаимодействием и полем Хиггса (3), частицы-духи, устраняющие избыточность поля Хиггса (4) и духи Фаддеева — Попова, влияющие на избыточность слабого взаимодействия (5). Массы нейтрино сюда не входят. Описывает всё, что мы знаем на сегодняшний день; это может и не быть полный Лагранжиан, описывающий 3 или 4 фундаментальных взаимодействия.

Всё это сводится к более общему вопросу: как и когда мы можем использовать математику для того, чтобы узнать что-либо по поводу нашей физической Вселенной? Мы не знаем, как, но знаем, когда: когда это согласуется с нашими экспериментами и наблюдениями. Пока все законы физики остаются законами физики, и не включаются или выключаются по капризу, и не меняются каким-то непонятным образом, мы знаем, что можем описать их математически, по крайней мере, в принципе. Поэтому, математика – это набор инструментов, которые мы используем для описания работы Вселенной. Это необработанные материалы: гвозди, доски, молотки и пилы. Физика – это то, как применять эту математику. Физика – это то, как собирать всё это вместе, чтобы все ваши материалы приобрели смысл и превратились, к примеру, в дом, вместо набора материалов, которые, в принципе, можно использовать для постройки чего-то совершенно иного.

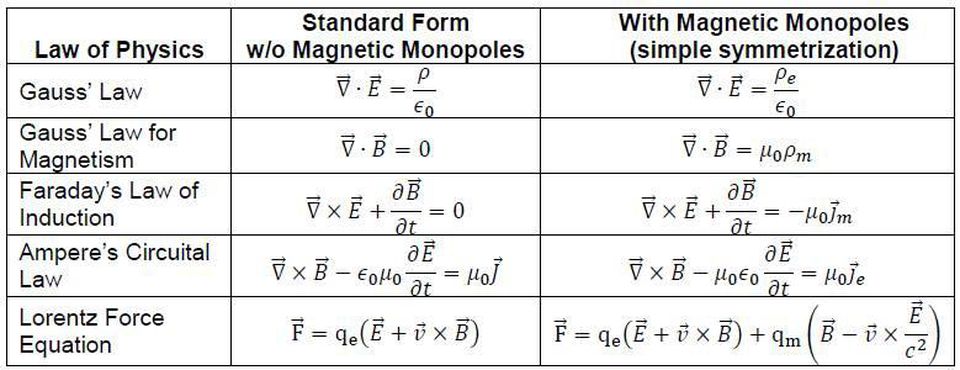
Вполне возможно записать разные уравнения, такие, как уравнения Максвелла, описывающие Вселенную. Мы можем записать их по-разному, но только сравнивая их предсказания с физическими наблюдениями, мы можем сделать какие-то выводы по поводу их истинности. Поэтому вариант уравнений Максвелла с магнитными монополями не соответствует реальности, а варианты без них – соответствуют.

Если что-то описывает Вселенную точно, и способно сделать численные предсказания, то это физика. Если эти предсказания оказываются точными и отражающими реальность, то это правильная и полезная физика. Если можно продемонстрировать ложность этих предсказаний, то это физика, не описывающая нашу Вселенную: это неудавшаяся физическая теория. Но если у уравнений нет никакой связи с физической Вселенной, и их нельзя связать ни с чем, что можно было бы надеяться когда-нибудь увидеть или измерить, это однозначно мир математики; тогда её отлучение от физики будет окончательным. Математика – это язык, используемый для описания физики, но не всё математическое имеет физический смысл. Связь между ними и её нарушение можно определить, только наблюдая за самой Вселенной.