Насколько большие Ваши яйца?

Добрый день, дорогие пользователи habr.com! Сегодня православные христиане празднуют Пасху, и мне кажется, что многие задаются вопросом: «Какой же объём у куриного (страусиного, перепелиного и т.д.) яйца»? Это действительно интересная математическая задача, которую мы с Вами постараемся решить в этой статье. Приятного чтения!

Рисунок 1. Пасхальные яйца

Начальные положения, определяемся с кривой

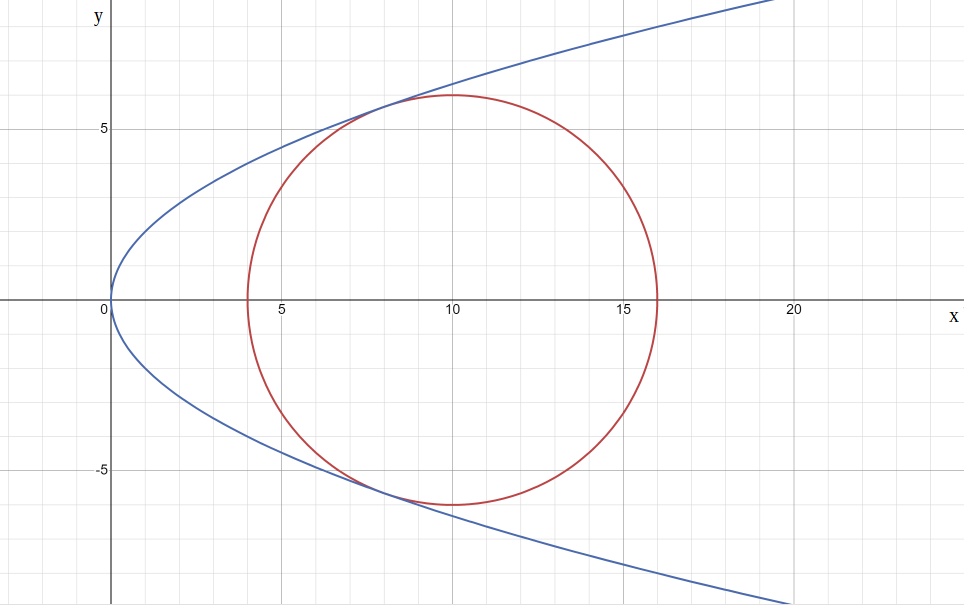
Рисунок 2. График яйца

Для начала определимся с функциями, которыми мы будем задавать наше яйцо.

Я предлагаю описывать наше яйцо следующей кусочно-заданной кривой:

При x ∈ [0, 8] cu:

$$

При x ∈ (8, 16] cu:

$$

(Уравнение окружности с центром в точке (10, 0) и радиусом 6.)

Чем обусловлен такой выбор? Полученная кривая в большей степени напоминает яйцо, чем любая другая кривая, составленная из двух уравнений. Точка касания окружности к кривой – целое число, она равна 8. Т. е. при дальнейшем интегрировании площади тела вращения (для нахождения объема) будем рассматривать его как сумму объемов двух различных тел вращения.

Объем тела вращения через определенный интеграл

Наша расчетная формула выглядит следующим образом:

$$

Уравнение 1. Формула объема тела вращения

И теперь просто считаем два объема:

Для x≥ 0 и x ≤ 8:

$$

$\$\$display\$\$V\; =\; \pi \int \_a^b\; f(x)^2\; dx\; =\; \pi \int \_0^8\; (4x)\; dx\; =\; \{4\pi x^2over2\}\; =\; 2\pi x^2=128\pi \$\$display\$\$$

Т.е. объем первой части тела вращения = 128π.

Для x>8 и x ≤ 16:

$$

Предлагаю во избежание трудностей принять a = 8.01

$\$\$display\$\$V\; =\; \pi \int \_a^b\; f(x)^2\; dx\; =\; \pi \int \_\{8.01\}^\{16\}\; (36\; –\; (x-10)^2)\; dx\; =\; \$\$display\$\$$

$$

Суммарный объем нашего яйца получается равным 318π у.е. или ≈ 998,997 у.е.

Напомню, что все расчеты велись в условных единицах и длина (читай высота) моего яйца – 16 у.е.

Из формулы подобия следует:

$$

Если ваше яйцо имеет длину, равную 58 мм, то его объем находится через пропорцию:

$$

V2 = 47571, 42 мм^3 = 47,57142 см^3

Истинность этого была подтверждена экспериментально:

Рисунок 3. Мензурка, наполненная водой на 500 мл

Рисунок 4. Яйцо вытеснило 47 мл, и уровень воды установился на отметке в 547 мл.

Спасибо, что прочли эту статью до конца! Светлой Пасхи Вам!