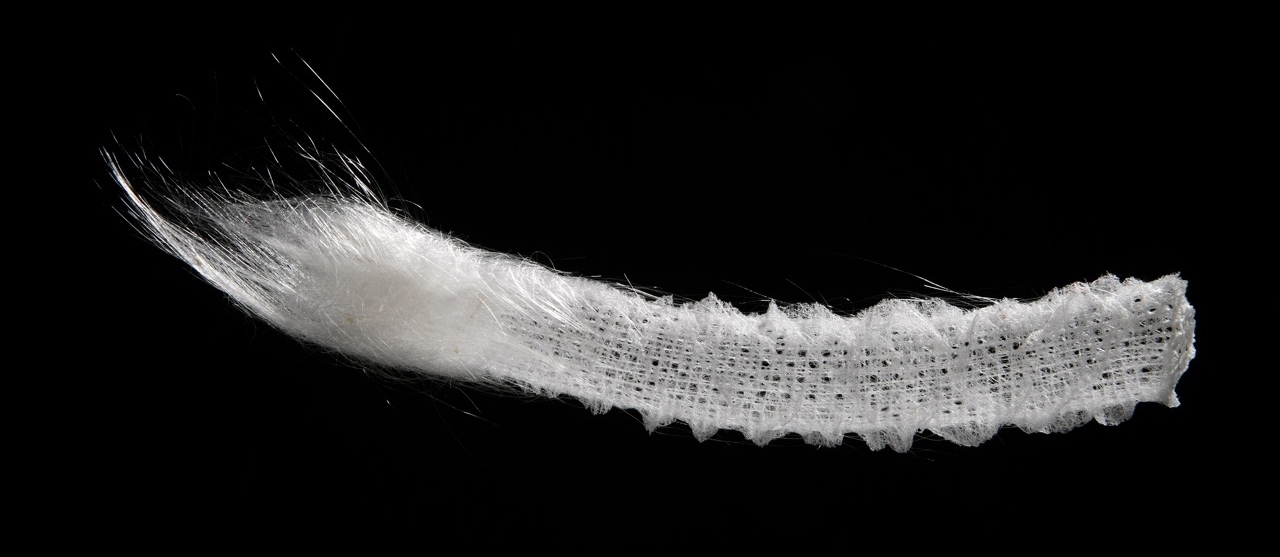
При упоминании словосочетания «морская губка» у кого-то в голове может возникнуть образ крайне популярного мультипликационного персонажа. Однако у лучшего работника Красти Краб нет ничего общего с его реальным прототипом. Визуально разные виды морских губок выглядят по-разному: древнегреческие амфоры, замысловатые духовые инструменты, высохшие ветки деревьев, причудливые цветы и т.д. Но за внешним обликом скрывается невероятно сложная клеточная структура, которая привлекает внимание научного сообщества уже не первый год. Исследователи из Гарвардского университета в своем недавнем труде выяснили, что структурные особенности строения морских губок могут послужить вдохновением для более прочных и высоких небоскребов, более длинных мостов и сверхлегких космических кораблей. Почему структура морской губки уникальная, каковы ее механические характеристики, и какие результаты показали прототипы, созданные на базе полученных данных? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.
Основа исследования
В мире насчитывается порядка 8000 видов морских губок, однако в данном исследовании особое внимание уделяется шестилучевым губкам (Hexactinellida). Этот тип губок также весьма многообразен, ибо насчитывает около 600 видов. Обитают они в морях на глубинах от 5 до более 6000 метров.
Свое имя шестилучевые губки получили из-за строения своего скелета, состоящего из шестилучевых кремниевых игл, которые расположены в трех взаимно перпендикулярных плоскостях.
Форма тела Hexactinellida может быть самой разной: трубчатая, кубковидная, комковидная, отростчатая, лопастная и т.д. Несмотря на визуальные отличия, состав тела у всех видов достаточно схож. Основой тела является единый синцитий*.
Синцитий* — тип ткани у живых организмов с неполным разделением клеток, когда обособленные участки цитоплазмы с ядрами связаны между собой цитоплазматическими мостиками.
Схема синцития стеклянной губки (Hexactinellida): синий — ток воды; темно-серый — спикулы; серый — синцитий; красный — хоаноцитные клетки.
Одной лишь схемы достаточно, чтобы понять, чем же так может быть полезна стеклянная губка в архитектуре или мостостроении.
В данном исследовании ученые рассматривали минерализованную скелетную систему губки вида Euplectella aspergillum (цветочная корзина Венеры), которая отличается уникальной иерархической архитектурой и механической прочностью во многих масштабах длины.

Euplectella aspergillum (вид сверху).
Стекловидные скелетные элементы (спикулы) E. aspergillum состоят из центрального белкового ядра, окруженного чередующимися концентрическими слоями консолидированных наночастиц кремнезема (диоксид кремния, SiO2) и тонкими органическими прослойками. Спикулы организованы таким образом, чтобы формировать квадратную сетку, усиленную двумя пересекающимися наборами парных диагональных распорок, создавая подобный шахматной доске узор чередующихся открытых и закрытых ячеек.
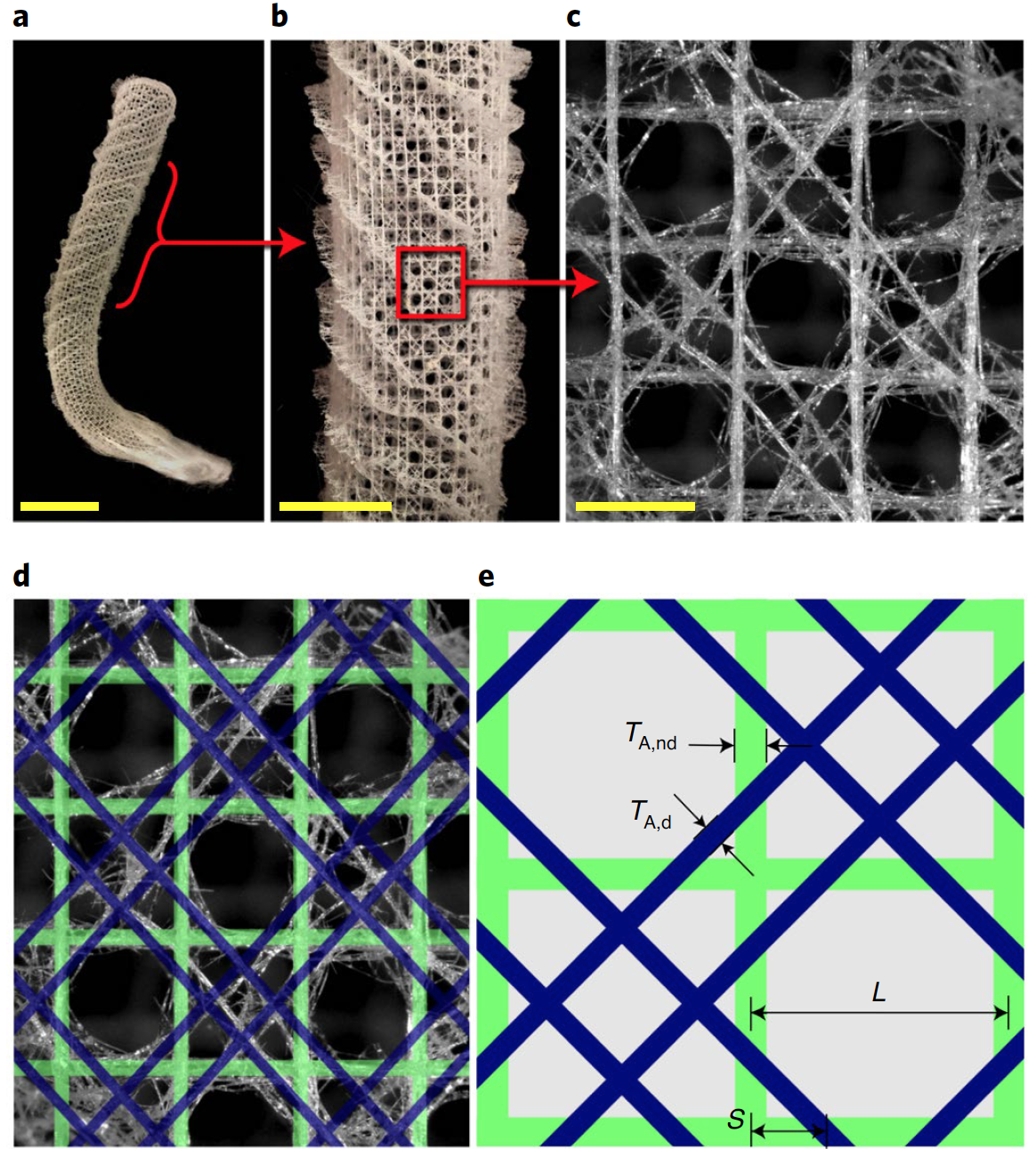
Изображение №1
Ранее влияние многослойной архитектуры спикул на замедление распространения трещин и на увеличение прочности на изгиб уже подвергались рассмотрению, но потенциальные механические преимущества двухдиагональной квадратной решетки, состоящей из спикул, не были удостоены особым вниманием.
Ученые напоминают, что сетчатые решетки с открытыми ячейками, такие как те, что встречаются в скелетной системе E. aspergillum, обычно используются в инженерном контексте из-за их меньшего веса, высокого поглощения энергии и способности контролировать распространение акустических и тепловых волн. Как правило, свойства и функциональность таких геометрических фигур зависят от типа и характеристик связи их узлов (точек пересечения).
Например, минимальное количество узловых соединений, равное шести, требуется для двумерных решеток, в которых преобладает растяжение, и тем самым достигается более высокое отношение прочности к весу для структурных приложений. Но решетки с простой квадратной геометрией (с соединением узлов, равным четырем), довольно нестабильны, когда вектор нагрузки имеет поперечный компонент, посему для стабилизации требуется диагональное соединение.
В рассматриваемом нами сегодня труде ученые использовали скелет E. aspergillum в качестве основы для создания механически прочных архитектур с квадратной решеткой. В ходе исследования были использованы экспериментальные и численные методы анализы для определения механических свойств скелетной решетки губки.
Результаты исследования
Чтобы лучше понять механические преимущества скелетной архитектуры губки, было проведено сравнение характеристик ее геометрии с характеристиками трех других двумерных решеток с квадратным основанием (у всех четырех вариантов был одинаков объем, т.е. одинаковое количество материала).
В каждой из этих структур базовая квадратная архитектура состояла из элементов с длиной L и прямоугольным поперечным сечением, характеризующимся глубиной H, которая достаточно велика, чтобы избежать деформации вне плоскости.
Вариант А, который был вдохновлен морской губкой, состоял из горизонтальных и вертикальных (недиагональных) элементов толщиной TA,nd = 0.1 L и двух наборов параллельных двойных диагоналей толщиной TA,d = 0.05 L, расположенных на расстоянии S = L / (√2 + 2) от узлов (2а).

Изображение №2
Вариант В также был основан на архитектуре губки с TB,nd = 0.1 L, но содержал только одну диагональ толщиной TB,d= 0.1 L, пересекающую каждую из замкнутых ячеек (2b).
Вариант С (TC,nd = 0.1 L) был основан на архитектуре, используемой в современных инженерных приложениях, имел набор перекрещенных диагональных балок с толщиной TC,d = 0.05 L в каждой ячейке (2c).
Вариант D не имел диагонального армирования, а его горизонтальные и вертикальные элементы были толщиной TD,nd = 0.1L(1 + 1/√2) (2d).
В первую очередь был проанализирован механический отклик при одноосном сжатии вдоль вертикальных элементов четырех вариантов решетки, описанных выше.
Образцы, содержащие 6х6 мозаики квадратных ячеек с L = 1.5 см и H = 4 см, были изготовлены на 3D-принтере Connex500 (Stratasys). Одноосное сжатие выполнялось посредством устройства Instron (модель 5969) с датчиком нагрузки 50 кН (2e).
На графике 2f показаны кривые напряжения-деформации, из которых можно сделать два основных вывода. Во-первых, все конструкции с диагональным усилением (варианты A, В и C) характеризовались почти идентичной начальной упругой реакцией, демонстрируя, что различные конструкции диагонального усиления не повлияли на исходную общую жесткость конструкции. Вариант D, как и ожидалось, показал более высокую исходную жесткость из-за более толстых вертикальных и горизонтальных элементов.
Во-вторых, все кривые показывают четкую максимальную несущую способность, причем конструкция A (вариант, вдохновленный губкой) выдерживает самую высокую нагрузку.
Поскольку каждая максимальная нагрузка соответствовала началу потери устойчивости, ученые пришли к выводу, что конструкция A показывает самое высокое критическое напряжение для потери устойчивости из всех рассмотренных вариантов.
Кроме того, было установлено, что во всех трех конструкциях с диагоналями, динамика после потери устойчивости привела к однородному преобразованию структуры по всему образцу (2e).
А вот у варианта D критическая мода привела к гораздо большей длине волны, чем размер квадратной ячейки, что после потери устойчивости привело к образованию формы, качественно аналогичной форме сжатой изогнутой балки.
Чтобы понять, как конструкция решетки, вдохновленная губкой, привела к существенному улучшению механических характеристик, было проведено моделирование методом конечных элементов с использованием программного обеспечения ABAQUS/Standard.
Для моделирования геометрия была построена с использованием балочных элементов Тимошенко (тип элемента ABAQUS B22), а реакция материала была зафиксирована с помощью модели несжимаемого материала с модулем сдвига μ = 14.5 МПа.
Процесс моделирования состоял из трех этапов:
- анализ потери устойчивости;
- затем к узлам сетки было применено возмущение в виде самой низкой формы потери устойчивости;
- статический нелинейный анализ для оценки нелинейных откликов при больших деформациях.
График 2f показывает очень близкое соответствие между численными и экспериментальными результатами.
Далее модель конечных элементов была намеренно расширена, чтобы изучить влияние направления нагрузки. Дабы снизить вычислительные затраты и устранить краевые эффекты, была использована периодичность структур и исследовалась реакция элементов репрезентативного объема (RVE) с подходящими периодическими граничными условиями.
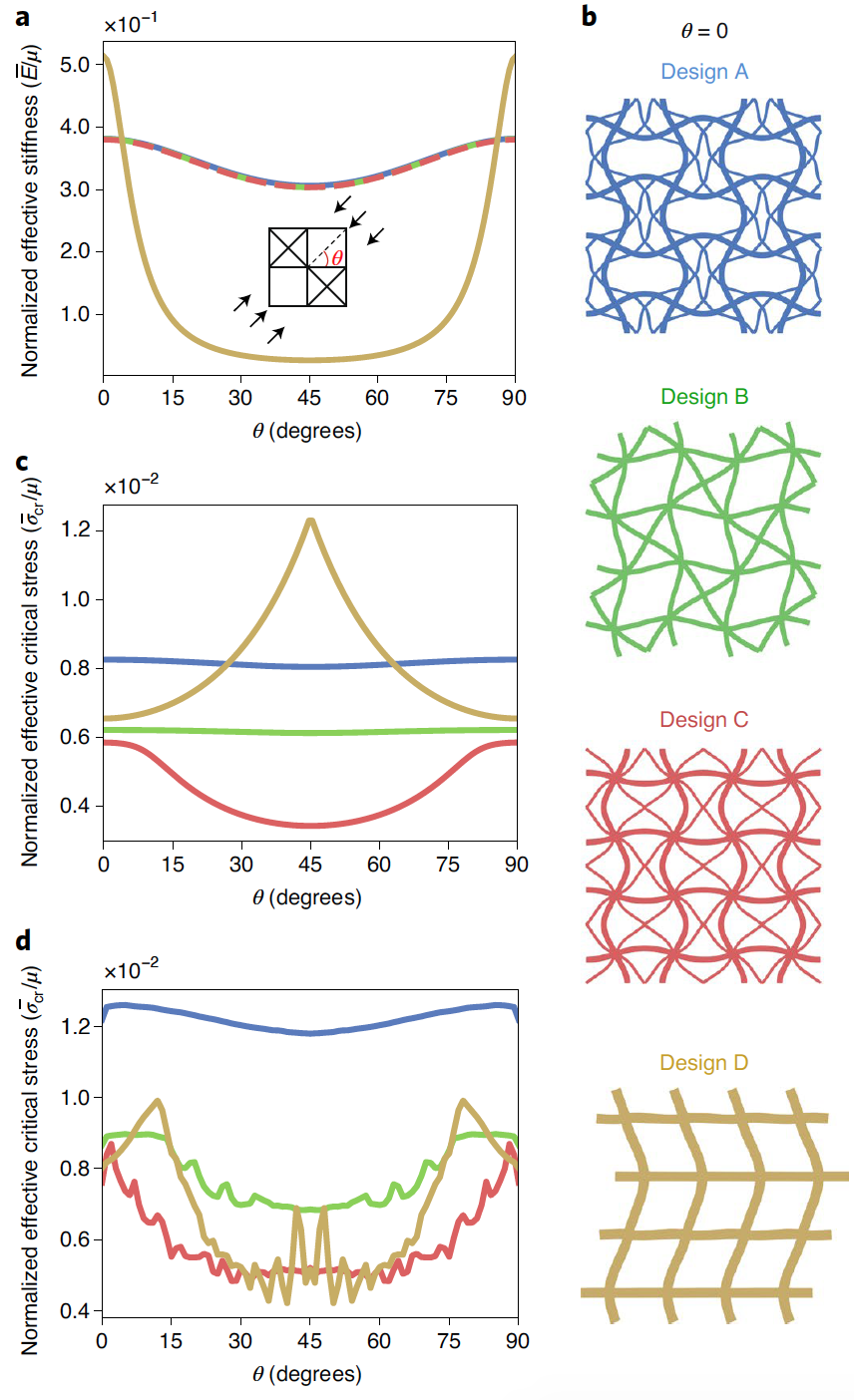
Изображение №3
На 3а показано изменение эффективной жесткости конструкции (E) в зависимости от угла нагрузки (θ). Было установлено, что жесткость всех конструкций, содержащих диагональное усиление, была практически одинаковой для любого угла нагрузки. Этот факт дополнительно подтверждает, что жесткость конструкции в основном определялась количеством материала, распределенного вдоль направления нагрузки.
В результате конструкция D, в которой весь материал был отнесен к недиагональным элементам, демонстрировала наивысшую жесткость при θ = 0°, но имела незначительную несущую способность для θ = 45°.
Далее было изучено влияние θ на характеристики продольного изгиба конструкций A – D. Эффективное критическое напряжение изгиба (̅σcr) конструкции A было выше, чем у других конструкций с диагональным усилением (конструкции B и C) для всех значений θ (3b). Конструкция D превосходит конструкцию A в промежутке 27°<θ<63°, если предположить, что эти конструкции бесконечны. Однако, учитывая глобальный характер режима потери устойчивости для конструкции D, на такие характеристики в значительной степени повлияли граничные эффекты, и критическое напряжение потери устойчивости было существенно снижено при рассмотрении конструкции с точно установленными размерами 10х10 RVE (3d). Кроме того, геометрия конструкции А сохраняла свою надежность даже после модификаций решетки путем введения различных уровней беспорядка, что согласуется с особенностями, наблюдаемыми в скелете морской губки.
Вышеописанные результаты моделирования и фактических испытаний четко говорят о том, что вариант конструкции А, основанный на скелете морской губки, явно превосходит своих соперников (варианты В, С и D). Однако на этом испытания не были окончены, ведь ученые задались вопросом, можно ли создать конструкцию, которая будет еще лучше.
Для этого была сформулирована задача по оптимизации, направленная на определение числа (N) диагональных элементов квадратной решетки, которое позволит достичь более высокого значения критического напряжения на изгиб. Также необходимо было установить расстояние между этими элементами и узлами соединений решетки Si (где i = 1, 2, …, N), а также соотношение диагональных и недиагональных элементов λ = Vnd/Vd (Vnd и Vd — объем недиагональных и диагональных элементов, соответственно). Все эти переменные так или иначе влияют на показатели напряжения изгиба.
Во время испытаний структуры размером 3х3 RVE подвергались одноосному сжатию, параллельному недиагональным элементам (θ = 0°). Целевая функция Z = ̅σcr была максимизирована с использованием моделирования методом конечных элементов в сочетании с Python реализацией алгоритма эволюции адаптации ковариационной матрицы (CMA-ES). Для каждого набора входных данных, определенных CMA-ES, был проведен анализ потери устойчивости методом конечных элементов для получения ̅σcr, который впоследствии использовался для оценки целевой функции Z.
Было проведено семь различных оптимизаций, каждая из которых рассматривала фиксированное целое число диагональных элементов N в диапазоне от одного до семи (N = ℤ ϵ [1, 7]). Для обеспечения симметрии системы учитывались следующие правила: S2i−1 = S2i (i = 1, 2,…, N/2), если N — четное число; S1 = 0 и S2i−1 = S2i (i = 2, 3,…, (N − 1)/2), если N — нечетное число.
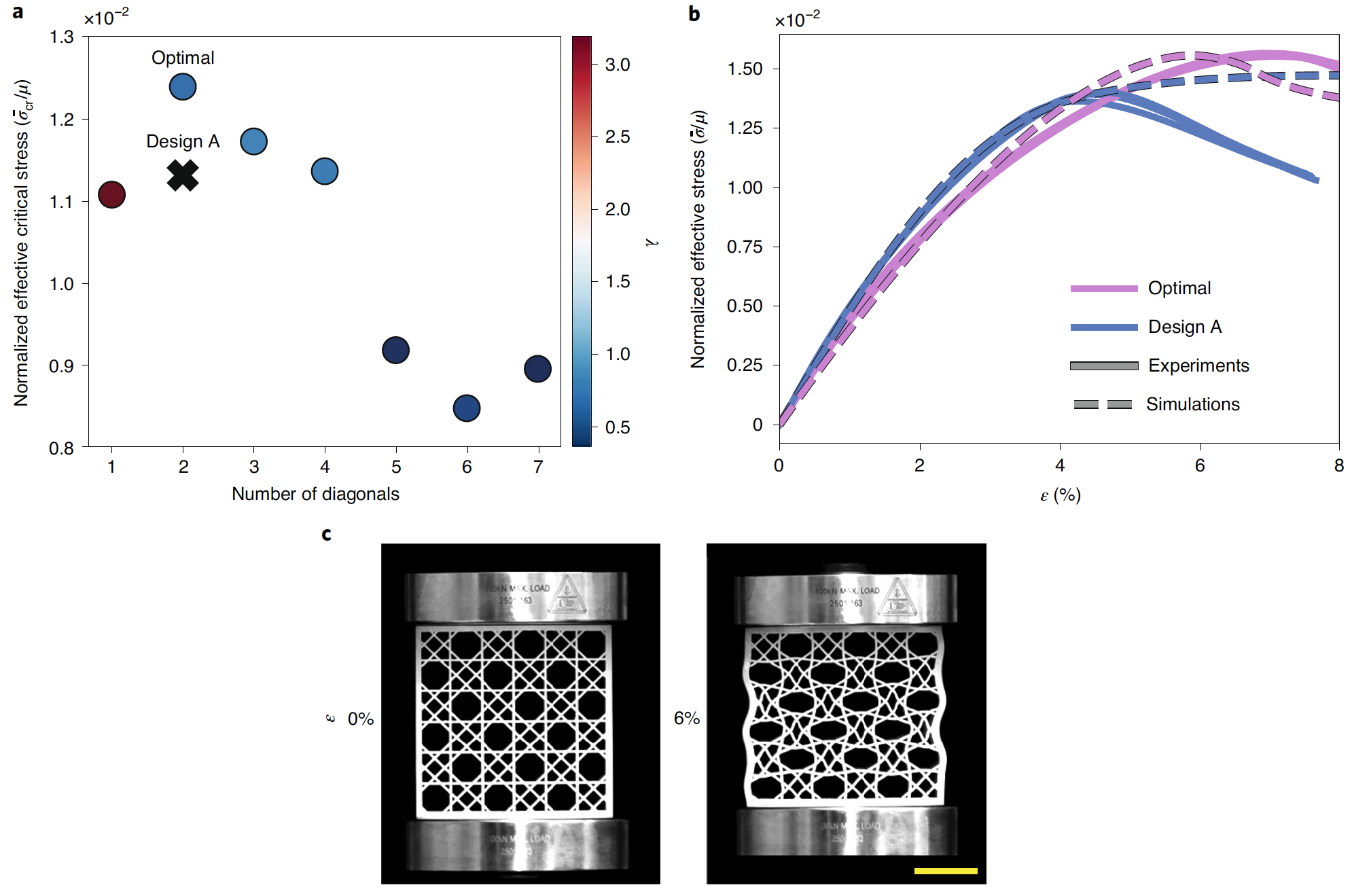
Изображение №4
На графике 4а показано самое высокое значение ̅σcr, определенное моделью CMA-ES для всех рассмотренных значений N. Было установлено, что самое высокое значение ̅σcr было всего лишь на 9.55% выше, чем в случае испытанной ранее конструкции А. В данном же тесте смоделированная конструкция также была вдохновлена морской губкой: две диагонали были расположены на расстоянии S = 0.1800 L от узлов, а распределение объема было таковым, чтобы λ = 0.6778). Результаты моделирования были успешно подтверждены экспериментально (4b).
Ученые отмечают, что скелетная структура морской губки E. aspergillum является отличным вдохновением не только для решетчатых архитектур (конструкция A). Для демонстрации этого на изображении 5а показана тонкая мозаика из 11х2 квадратных ячеек, на которую воздействует трехточечное напряжение изгиба.
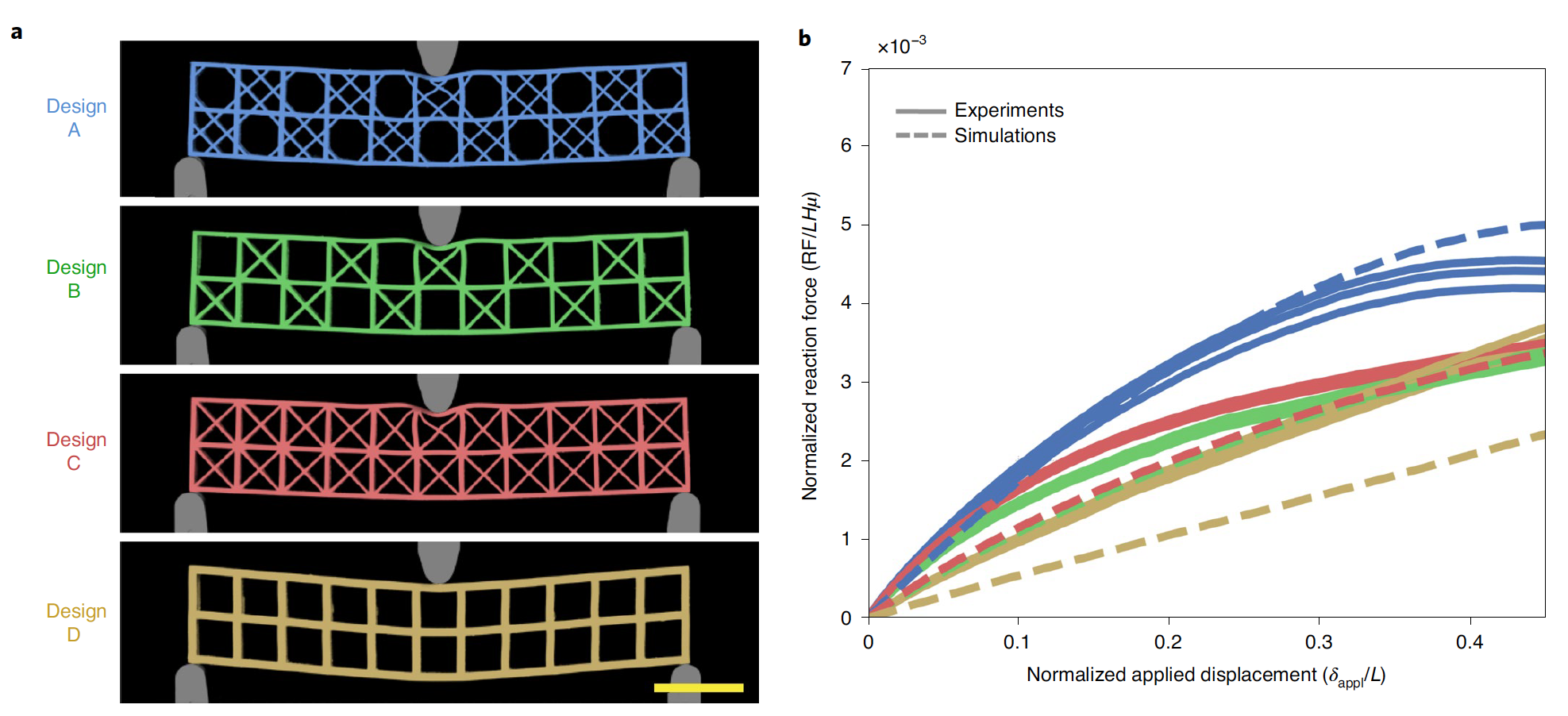
Изображение №5
Как эксперименты (5b), так и моделирование методом конечных элементов продемонстрировали, что конструкция, вдохновленная губкой, была более жесткой и могла выдерживать на 15% более высокие нагрузки в более широком диапазоне приложенных смещений.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
Природа всегда была, есть и будет одним из основных источников вдохновения для научных изысканий. В данном труде это утверждение было подтверждено на примере морских губок вида Euplectella aspergillum, чья скелетная структура обладает удивительными характеристиками. Основная особенность заключается в том, что эта биологическая структура способна выдерживать значительные нагрузки, при этом в ее постройке задействован минимальный объем материала. Другими словами, морские губки достаточно пористые (грубо говоря), но при этом очень прочные.
Проведенное исследование показало, что архитектура скелета морской губки может быть крайне полезна в самых разных сферах деятельности человека. Внедрение архитектуры морской губки в строительстве позволит создавать более высокие небоскребы и более длинные мосты, при этом будет потрачено оптимальное количество материала, а прочность готовых сооружений при этом не пострадает. Данную технику также можно применить в самолетостроении, судостроении и даже в космонавтике, ведь минимизация массы судна позволит минимизировать расходы топлива.
Благодарю за внимание, оставайтесь любопытствующими и отличных всем выходных, ребята! 🙂
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?



