Импортозамещение, потерянное навсегда: история первых серийных троичных компьютеров «Сетунь»

Многие знают, что СССР был родиной т.н. “троичных машин”, т.е. компьютеров, использующих не двоичную, а троичную систему счисления. Они стали уникальной страницей в истории вычислительной техники. Единственный серийный и самый известный пример троичной ЭВМ — советский компьютер «Сетунь», разработанный в 1958 году под руководством Николая Брусенцова, при активном участии Льва Гутенмахера и Сергея Соболева, а затем модернизированный к началу 70-х.

Многими троичная логика считалась нетривиальной, но тупиковой ветвью развития вычислительной техники. Однако сегодня интерес к этой теме возрождается, ввиду неочевидных, но существенных преимуществ троичных систем в определенных видах вычислений, этого я также коснусь, завершая эту статью.

Создатели 

Компьютер “Сетунь” был разработан в Вычислительном центре Московского государственного университета в 1959 году. Основными разработчиками, помимо Николая Брусенцова, были Евгений Жоголев, В. В. Веригин, С. П. Маслов и А. М. Тишулина. Разработка машины была предпринята по инициативе и осуществлялась при активном участии советского математика Сергея Соболева.

Толчком к созданию машины стали работы Льва Гутенмахера, известный своими работами в области магнитных элементов. Гутенмахер считается одним из пионеров в области создания вычислительной техники, в частности он заложил основы использования компьютера для моделирования когнитивных и лингвистических процессов.

В 1950 году он возглавил создание электронной вычислительной машины, которая использовала феррит-диодные бесконтактных реле на основе магнитных усилителей трансформаторного типа. Они получили название двоичной ферритодиодной ячейки Гутенмахера. К 1954 году на их основе была создана безламповая ЭВМ ЛЭМ-1. Взяв за основу ячейки Гутенмахера, команда Брусенцова разработала троичную ферритодиодную ячейку, которая легла в основу «Сетунь”. Подробно об устройстве ферритовых элементов можно почитать здесь.

Как объяснял Брусенцов в одном из своих интервью, оригинальность выбранной элементной базы была «не от хорошей жизни». Использование радиоламп для компьютеров представлялось создателям “Сетуни” плохой идеей, в силу их ненадёжности и нестабильности, высокого энергопотребления, бессмысленного для производительности усложнения схемотехники, а также высокой стоимости конечных решений.

Ещё одна проблема заключалась в остром дефиците транзисторов. Полупроводниковая схемотехника привлекала создателей, но транзисторы в СССР середины 50-х годов были как секс, создавались в ничтожных количествах, исключительно в лабораториях. Во многом это было связано с решениями советского руководства. По легенде в 1956 году в Совмине состоялось совещание генеральных конструкторов, итогом которого стал прогноз о то, что: «Транзистор никогда не войдет в серьёзную аппаратуру. Перспективой применения транзисторов могут быть разве что слуховые аппараты. Пусть этим занимается Министерство социального обеспечения».

Ещё одним советским учёным, сыгравшим ключевую роль в создании “Сетунь 1” стал академик Сергей Соболев. В тот момент он возглавлял кафедру вычислительной математики МГУ. Ему принадлежала концепция, именно он предложил идею разработки малой ЭВМ специально для использования на кафедре в 1955 году и поручил эту работу Брусенцову.

По воспоминаниям Брусенцова, первоначально в МГУ планировали использовать ЭВМ М-2. Однако поддержка Сергея Соболева в пользу Сергея Алексеевича Лебедева вместо кандидатуры Иосифа Брука, главного конструктора М-2, на выборах в АН СССР лишила МГУ возможности получить этот компьютер и создала ситуацию, в которой возникла необходимость в создании новой машины.

Математическую базу, которая обеспечила создание “Сетуни”, совместно с Брусенцовым разрабатывал математик и программист Евгений Жоголев.

В дальнейшем результаты, полученные при разработки и эксплуатации “Сетунь” и других ЭВМ, легли в основу его кандидатской диссертации «О логических структурах и математическом обслуживании малых цифровых автоматических машин», которую он защитил в 1963 году. 

“Сетунь” и “Сетунь 70”

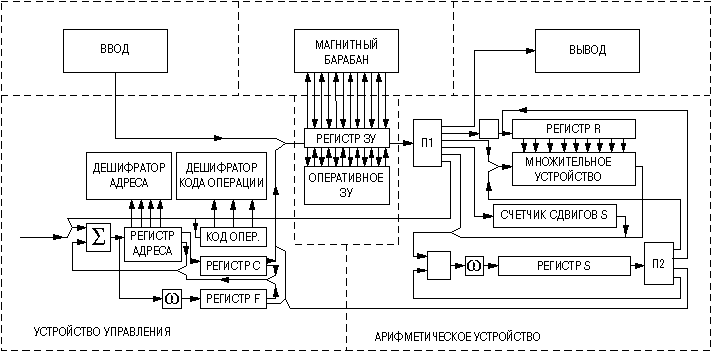
«Сетунь» использовала сбалансированную троичную систему счисления и трехзначную логику, что отличало его от преобладающих как тогда, так и сейчас двоичных систем. Это позволяло сократить количество необходимых элементов и уменьшить энергопотребление. Компьютер имел оперативную память на 81 слово, каждое из которых состояло из 18 тритов (троичных цифр), а также дополнительную память на магнитном барабане на 1944 слова, что в сумме составляло около 7 КБ. Такими были системные характеристики машины в 1959 году.

 “Сетунь” стала ещё и первым серийным троичным компьютером. Всего было выпущено 46 ЭВМ «Сетунь». Производство осуществлялось на Казанском математическом заводе. 30 компьютеров использовались в университетах СССР, остальные, вероятно, применялись в народном хозяйстве и использовались для военных целей.

Как отметила в своем посте об этом компьютере @TashaFridrih: “начиная с 1959 года Сетунь за полтора месяца вывела больше расчетов, чем ЭВМ Урал-2 с двоичной системой счисления”, при равном количестве машиночасов. Создатели и эксплуатанты “Сетунь 1” отмечали её высокую надёжность.

Низкая себестоимость “Сетунь” сыграла злую шутку с ЭВМ. По признанию самого Брусенцова: «Сетунь мешала людям с косным мышлением, которые занимали высокие руководящие посты».

Парадоксально, но советским чиновникам не нравился компьютер с низкой себестоимостью, на тот момент она составляла всего 37 500 рублей, что значительно ниже, чем у большинства компьютеров того периода. 

В 1967-1969 годах на основе машины Сетунь была разработана новая архитектура троичного компьютера «Сетунь-70», в которой были реализованы идеи структурированного программирования Эдсгера Дейкстры, реализованные в аппаратной части машины. Языком создателя был реализован принцип «нетрадиционной двухстековой архитектуры, ориентированной на обеспечение благоприятных условий дальнейшего развития ее возможностей методом интерпретирующих систем».

«Сетунь-70» имел короткий набор инструкций, разработанный Брусенцовым независимо от принципов RISC-архитектуры. Мелкосерийный выпуск продолжался в период с 1959 по 1965 год, Крупную серию планировали только через 15 лет, однако так и не начали, несмотря на апгрейд в виде “Сетунь-70”. Первый компьютер единственной серии, созданный в 1959-м, прослужил 15 лет, а затем был разрезан автогеном и отправлен на утилизацию.

“Наставник”

Сетунь-70” стал основой для одной из первых (если не первой) в СССР систем компьютерного обучения — “Наставник”. Во многом эта система позволила проекту развиваться, так как нетипичность архитектуры и элементной базы семейства “Сетунь” к 70-м годам настроила против команды разработчиков ряд лиц, принимающих решения, в основном из руководителей электронной промышленности СССР. Чтобы продемонстрировать эффективность “Сетунь-70”, Брусенцов инициировал проект «Разработка автоматизированной обучающей системы на базе малой цифровой машины» профессором МВТУ имени Баумана Анисимовым (могу ошибаться, но, вероятно, речь о Владимире Ивановиче Анисимове).

Для разработки системы был изучен американский опыт автоматизации обучения, так в своём интервью о «Наставнике» Хосе Рамиль Альварес пишет:

«Изучив результаты пятилетнего тестирования в США популярных систем обучения PLATO IV и TICCIT, в основу нашей системы, названной «Наставник», было решено положить принцип «книга + компьютер»: учебным материалом была особенным образом организованная книга, а компьютер для достижении требуемой степени усвоения материала управлял подачей материала и заданием упражнений и пояснениями на ошибочные ответы.»

Итогом проекта стала разработка программно-аппаратного комплекса “Наставник” для «Сетунь-70», ведущим разработчиком которой стал Хосе Рамиль Альварес. Для СССР “Наставник“ стал уникальной обучающей средой, со своей методологией. Однако уже на старте проекта Николай Брусенцов был уверен в том, что у системы нет серийного будущего. По воспоминаниям Альвареса, он объяснял это двумя обстоятельствами:

1. Низкая стоимость производства

2. Система не даст возможность “халтурить” ни студенту, ни преподавателю.

Испытания “Наставник“ проходил со студентами академика Николая Бахвалова, с кафедры вычислительной математики МГУ, у которого из-за незапланированной командировки мог сорваться коллоквиум по численным методам. Бахвалов создал шаблоны заданий для “Наставника”. Коллоквиум успешно прошёл без его личного участия. После это “Наставник” стал регулярно использоваться на кафедре. 

Альварес вспоминал, что во время пересдачи тестов на “Наставнике”, он и Бахвалов наблюдали, как один из студентов садился за один и тот же терминал “Сетуни-70”, полагая, что получит те же вопросы, что и в прошлый раз. Однако вопросы выбирались случайным образом, программа использовала в качестве основы для генерации случайных чисел подсчет числа нажатий на клавишах терминала всей аудитории. 

Полноценная эксплуатация “Наставник“ началась в 1974 году, для этого в МГУ был оборудован компьютерный класс на базе «Сетуни-70», к ней были подключены 27 терминалов. Система ограниченно использовалась для изучение курса численного анализа и была рассчитана на 150 студентов. В дальнейшем был реализован курс обучения языку Фортран.

От эксперимента к забвению

Троичные компьютеры, несмотря на свои технические преимущества, были постепенно забыты в пользу двоичных систем. Причиной забвения стала сложность создания надежных устройств, работающих с тремя состояниями. Как известно, транзисторы, использующиеся в логических схемах, либо полностью закрыты, либо полностью открыты. 

 Элементы “Сетуни“ трехфазные феррит-диодные логические элементы сложно поддавались миниатюризации. Для 1970-х, когда в СССР выпускалось худо-бедно достаточное количество транзисторов, выглядели громоздкими и малоэффективными. Преимущества троичных вычислений не могли дать тот прирост вычислительной мощности, который позволяли получить транзисторные компьютеры с двоичной логикой. 

Создание новых полупроводников, которые могли бы надежно работать в трех состояниях, требовало бы разработки принципиально иной элементной базы и, очевидно, привело бы к огромным ресурсным затратам. При этом “Сетунь” была уникальной с точки зрения надёжности системой. По данным Брусенцова и Альвареса: 

“Опытный образец машины за 17 лет эксплуатации в ВЦ МГУ, после замены на первом году трех элементов с дефектными деталями, не потребовал никакого ремонта внутренних устройств и был уничтожен в состоянии полной работоспособности. Серийные машины устойчиво функционировали в различных климатических зонах от Одессы и Ашхабада до Якутска и Красноярска при отсутствии какого-либо сервиса и запчастей.” 

Ещё одной проблемой развития троичных компьютеров и причиной забвения “Сетуни” стала совместимость с устройствами “двоичного мира”. Троичные системы должны были бы поддерживать нетривиальные и сложные операции преобразования, а это предполагает рост их сложности и стоимости, а также ставит под вопрос эффективность использования троичной логики. 

“Сетунь” попала в уникальный период, когда дефицит элементной базу сыграл на руку авторам смелой технической идеи и способствовал выделению ресурсов на её разработку. Несмотря на то, что позже «Сетунь» был заменен на более традиционные двоичные компьютеры, его стоимость была в 2,5 раза ниже, что подчеркивает потенциальную экономическую эффективность троичных систем. 

Немного о принципах работы троичных компьютеров

Функция двоичный_поиск(массив, ключ)
    левая == 0
    правая == длина(массив) - 1
    Пока левая <= правая
        середина == (левая + правая) / 2
        Если массив[середина] == ключ
            Вернуть середина
        Если массив[середина] < ключ
            левая == середина + 1
        Иначе
            правая == середина - 1
    Вернуть -1
Конец функции

 левая == 0
    правая == длина(массив) - 1
    Пока левая <= правая
        первая_треть == левая + (правая - левая) / 3
        вторая_треть == правая - (правая - левая) / 3
        Если массив[первая_треть] == ключ
            Вернуть первая_треть
        Если массив[вторая_треть] == ключ
            Вернуть вторая_треть
        Если ключ < массив[первая_треть]
            правая == первая_треть - 1
        Иначе если ключ > массив[вторая_треть]
            левая == вторая_треть + 1
        Иначе
            левая == первая_треть + 1
            правая == вторая_треть - 1
    Вернуть -1
Конец функции

Функция троичное_сложение(троичное_число1, троичное_число2)
    Переменные:
        перенос == 0
        результат == пустой_список
    Для i от 0 до длины_большего_числа
        сумма == троичное_число1[i] + троичное_число2[i] + перенос
        Если сумма > 1
            перенос == 1
            сумма == сумма - 3
        Иначе если сумма < -1
            перенос = -1
            сумма == сумма + 3
        Иначе
            перенос == 0
        результат.добавить(сумма)
    Если перенос != 0
        результат.добавить(перенос)
    Вернуть результат
Конец функции

Перспективы троичных вычислений

P.S.

Тема первого троичного компьютера и современных разработок в вычислений не маленькая и даже формат лонгрида не позволяет осветить её достаточно полно. Поэтому я настоятельно рекомендую источники, которые я использовал при подготовке этого поста:

Источник