
Сообщество игры «Жизнь», клеточного автомата, изобретённого Джоном Конвеем, с давних пор стремилось найти осцилляторы — стабильные конфигурации, которые повторяются с определённой периодичностью во времени — для каждого натурального числа. И вот, наконец, 21 июля 2023 года был найден осциллятор для последнего недостающего периода — 41, завершая таким образом доказательство омнипериодичности.
В этой статье я расскажу историю открытия осцилляторов для всех периодов до 42 включительно, а также про семейство осцилляторов, включающее любой период от 43 и выше.
Зарождение игры «Жизнь» и первые осцилляторы
Официальным появлением на свет игры «Жизнь» можно считать публикацию Мартина Гарднера в журнале Scientific American в 1970 году с описанием этого автомата и нескольких небольших конфигураций. В ней описываются, среди прочего простейшие стабильные конфигурации (их также можно считать осцилляторами с периодом 1), самая маленькая из которых — блок; блинкер — осциллятор с периодом 2, а по совместительству — самая маленькая неумирающая конфигурация; восьмёрка — осциллятор с периодом 8 и похожий на цифру 8; пульсар — большой (но часто встречаемый, поскольку регулярно возникает из небольших конфигураций) симметричный осциллятор с периодом 3 и, наконец, пентадекатлон — осциллятор с периодом 15, возникающий в результате эволюции конфигурации 10 клеток в ряд. Из них все были обнаружены Джоном Конвеем, кроме восьмёрки, которую нашёл Саймон Нортон.
В первые два года (1970-1971) было исследовано довольно много небольших конфигураций, что позволило обнаружить несколько новых осцилляторов. Вертушка — найденный Саймоном Нортоном осциллятор с периодом 4 — относится к классу «бильярдных столов» — конфигураций, в которых статичная часть окружает центральную зону, в которой и происходит вся движуха. Восьмиугольник 2 — осциллятор с периодом 5, найденный независимо Солом Гудманом и Артуром Табером — выглядит как восьмиугольник в одной из фаз. Тумблер — красиво «щёлкающий» туда-сюда осциллятор с периодом 14 — найден Джорджем Коллинзом.
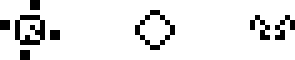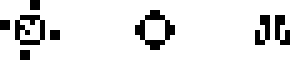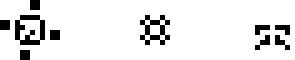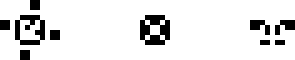
Билл Госпер исследовал движущиеся конфигурации и искал возможности их стабилизировать, то есть найти такое взаимодействие, которое предотвращает нежелательный бурный рост, погружающий всё вокруг в хаос. В результате им были обнаружены так называемые шаттлы — осцилляторы, в которых нестабильный объект перемещается из стороны в сторону и стабилизируется другими объектами (обычно статичными) по краям. Одним из них является шаттл пчелиной матки, имеющий период 30.
Кстати, если расположить две пчелиные матки определённым образом, чтобы они двигались навстречу друг другу, и поставить два блока по краям для стабилизации, то получится глайдерное ружьё Госпера — первая найденная конфигурация с неограниченным ростом:
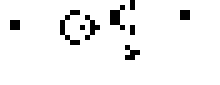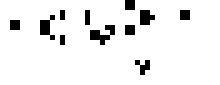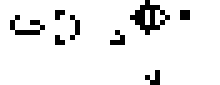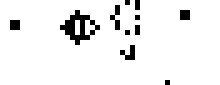
70-е и 80-е. Давид Бакинэм и Роберт Уэнрайт.
Давид Бакинэм — один из ранних энтузиастов игры «Жизнь». Основным объектом изучения у него были осцилляторы и глайдерный синтез (контролируемое столкновение глайдеров, образующее желаемую конфигурацию). Роберт Уэнрайт — математик и автор информационного бюллетеня «Lifeline», способствовавшему поддерживанию интереса к игре «Жизнь» на её ранних этапах. Какие же новые периоды были обнаружены благодаря им?
$rats и бурлоафериметр, оба найдены Давидом — экземпляры «бильярдных столов», уже чуть более сложной формы — имеют периоды 6 и 7, соответственно. Рабочая пчела и обеденный стол — примеры хасслеров, осцилляторов, в которых какой-либо объект регулярно «беспокоится» другими объектами, что позволяет поддерживать активную реакцию. В «рабочей пчеле» Давида хасслится искра (класс быстро умирающих конфигураций) с периодичностью в 9 тиков, а в «обеденном столе» Роберта 4 пожирателя (стабильная конфигурация из 7 клеток, имеющая свойство необычно хорошо подавлять другие реакции, оставаясь неизменной) по очереди «кусают» пре-улей (сам улей — стабильная конфигурация из 6 клеток, по форме похожая на пчелиную соту).

Пока что все осцилляторы были относительно маленькими. Но, что, если начать мыслить шире и использовать симметрию? Возможно, так думал Давид Бакинэм, когда строил «новыйшаттл» — осциллятор с периодом 28, в котором пре-пульсар поддерживается пожирателями (и их вариантами) с одной стороны и другими копиями пре-пульсара — с другой. Красиво, согласитесь?

Осцилляторы выше были найдены в 1972-м и 1973-м году. После этого скорость обнаружения новых периодов для осцилляторов несколько уменьшилась. До 1976-го включительно были найдено только два новых периода меньше 43: 10 и 13.
Здесь стоит пару слов сказать о систематическом именовании. Генрих Кёниг для своего каталога объектов игры «Жизнь» (был ранее доступен на сайте pentadecathlon.com) придумал способ идентификации разных объектов по систематическому имени, отражающему тип объекта. Для осцилляторов это #P#, где первое число — минимальное количество живых клеток среди всех фаз осциллятора, а второе — период. В случае, если несколько объектов имеют одинаковые имена, к ним добавляется индекс в каталоге после точки.
42P10.3, как можно судить из названия — безымянный (кроме систематического имени) осциллятор с периодом 10, относящийся к классу «бильярдных столов». p13 Бакинэма (сокращение от «period 13»), в котором активный регион держится под контролем двумя пожирателями-2
.В 1977-м и 1978-м всё тот же Бакинэм нашёл 38P11.1 (почти «бильярдный стол», но, поскольку он не полностью «закрыт», таким не считается) и гурмана — симметричный осциллятор, «гоняющий» пи-гептамино по кругу.
В 1980-м и 1983-м Бакинэм нашёл ещё пару способов сделать шаттл из пре-пульсара, добавив 29 и 26 к списку периодов.


Роберт Уэнрайт тем временем обнаружил парочку хасслеров: «Два пре-L хасслера» с периодом 16 и p36 хасслер жабы (жаба — довольно часто встречающийся осциллятор с периодом 2), в котором жаба каждые 18 тиков зеркально отражается.
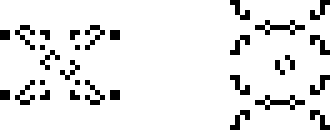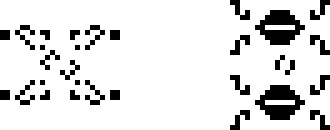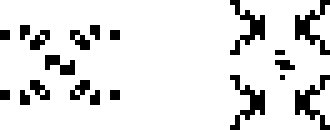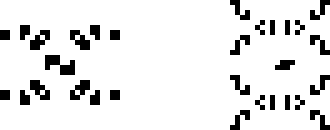
И, наконец, ещё два осциллятора Бакинэма: 117P18 и p40 шаттл B-гептамино.
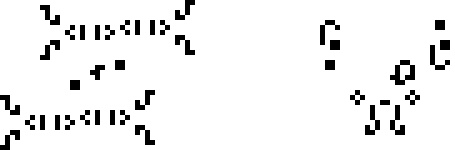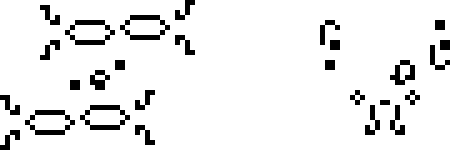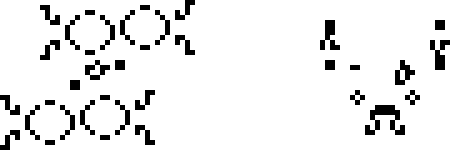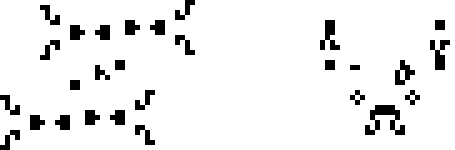
Интерлюдия: нетривиальность осцилляторов и НОК-осцилляторы
Давайте представим, что вам нужно найти осциллятор с периодом 36, а на дворе сейчас наступило лето 1980-го, осцилляторов известно не так много, и, вообще говоря, не очень-то и понятно, как можно было бы искать осциллятор с конкретным периодом. Тут бы хоть какой новый период найти — уже радость. Но тут вам в голову приходит идея — а что если взять осциллятор с периодом 4, осциллятор с периодом 9, поставить их рядом друг с другом (о!, а ещё лучше — друг на друга, чтобы их нельзя было расцепить), и обозвать это осциллятором с периодом 36 (ведь наименьшее общее кратное, НОК, 6 и 9 — это как раз 36)?
«Гениально!» — подумаете вы. «Тривиально», — скажут вам математики.
— Но почему?
— Как минимум, этот осциллятор можно разделить на два независимых, уже известных осциллятора.
— Ну, вообще-то, нельзя, я об этом уже подумал.
— Хм, действительно. Тогда будем называть осциллятор тривиальным, если нет ни одной клетки, период которой равен периоду осциллятора.
— … Я попозже приду.
Что нужно, чтобы сделать так, чтобы хоть одна клетка осциллировала с полным периодом? Желательно как-то заставить взаимодействовать осцилляторы, но так, чтобы они сами при этом не разрушились. Наверное, лучше всего для этого подойдут искрящие осцилляторы — те, которые возле краёв выбрасывают быстро умирающие кусочки. Если взять два таких осциллятора, и поставить их рядом так, чтобы их области искр пересекались или касались, то искры смогут взаимодействовать раз (или чаще) в общий период и образовывать ту самую желанную клетку (или несколько) с периодом, равным периоду осциллятора.
Вдохновившись этой идеей, вы начинаете искать искрящие осцилляторы с периодом 4 и 9. С последним всё хорошо — уже есть «закуска», найденная Марком Нимецом в 1972. Но вот с периодом 4 грустно: все осцилляторы — бильярдные столы или около того, и движущаяся часть у них внутри. Но тут Роберт Уэнрайт находит эмулятор среднего космического корабля — интересный осциллятор, выпускающий такую же искру, которую выпускает средний космический корабль (конфигурация, смещающаяся на 2 клетки вдоль кардинального направления каждые 4 тика), но без смещения. Обрадовавшись, вы стыкуете эмулятор и закуску вместе, и получается следующее:

Математики вздыхают, но соглашаются, что ваш осциллятор подходит под определение нетривиального. Но говорят, что в каком-то смысле ничего принципиально нового в нём нет, это всё ещё объединение двух других осцилляторов. И называют такие конфигурации НОК-осцилляторами (где НОК — наименьшее общее кратное).
Раньше такие конфигурации также считались тривиальными и особо не рассматривались как примеры осцилляторов нужных периодов. Сейчас консенсус сообщества состоит в том, что эти осцилляторы представляют отдельный класс нетривиальных осцилляторов.
90-е. Дин Хикерсон, Давид Эппштейн и Ноам Элкис
Дин Хикерсон — математик и энтузиаст игры «Жизнь». Написал первую программу для поиска осцилляторов, благодаря которой смог найти много маленьких осцилляторов с небольшим периодом, а также несколько крупнопериодических. Ноам Элкис — математик, привнёсший в игру «Жизнь», среди прочего, несколько новых периодов осцилляторов, и доказательство того, что максимальная плотность бесконечной стабильной конфигурации —. Давид Эппштейн — математик, профессор Калифорнийского Университета, а также автор программ для поиска осцилляторов и космических кораблей в игре «Жизнь», благодаря которым было получено внушительное количество новых объектов в этих категориях.
С появлением программ для поиска, новые осцилляторы стали появляться довольно быстро. Новые осцилляторы, но не новые периоды. Дело в том, что сложность растёт экспоненциально при увеличении желаемого периода (насколько известно автору), и на практике можно найти только осцилляторы небольших периодов. Однако, искрящие осцилляторы небольших периодов можно использовать для получения новых хасслеров.
В 1994 году были найдены 186P24 (Билл Госпер) и 134P25 (Ноам Элкис).

В 1995 году были найдены 145P20, 124P21 и p35 хасслер улья. Их открыли Ноам Элкис, Роберт Вэйнрайт и Дин Хикерсон, соответственно. Здесь уже вовсю эксплуатируются искрящие осцилляторы.

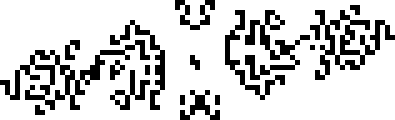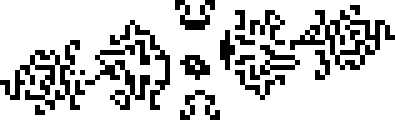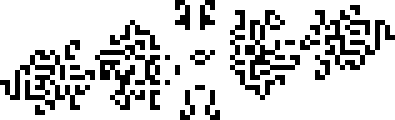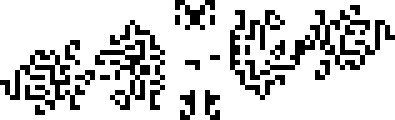
Интерлюдия 2: Открытие дорожек для Гершелей.
Гершель в игре «Жизнь» — это определённое гептамино, которое весьма часто появляется в процессе эволюции случайных конфигураций.
Мне понадобилось сгенерировать первичный бульон (так называется начальная конфигурация со случайным заполнением, как правило, 50%, часто используемая для исследования частоты появления различных конфигураций) всего 3 раза, чтобы получить красивый пример возникновения Гершеля:

Одной из особенностью Гершеля (а также его регулярно встречающегося предшественника — Б-гептамино) является его способность продвигаться вперёд в поле игры Жизнь, оставляя довольно мало следов позади себя (самый ранний из которых — это глайдер, которого можно спокойно съесть). Оказывается, если определённым образом расставить стабильные конфигурации (как правило, блоки и пожиратели, хотя встречаются варианты и поэкзотичнее) вокруг примерной зоны реакции, можно её «приручить» и заставить двигаться туда, куда мы хотим (не куда угодно, конечно, но выбор довольно большой).
Давид Бакинэм летом 1996-го года обнаружил это свойство Гершелей и сконструировал первые дорожки для них — конфигурации из статичных компонент, принимающие на свой вход Гершеля или Б-гептамино (или, в общем случае, другие активные регионы), и выдающие на выход также Гершель или Б-гептамино. Из-за того, что оба этих гептамино двигаются довольно активно, оказывается, что количество возможных стыковок таких дорожек довольно большое и позволяет направлять реакцию в произвольную сторону. В частности, можно замкнуть такую дорожку в цикл и получить осциллятор:

Открытие дорожек для Гершелей оказалось, пожалуй, самым революционным в истории игры «Жизнь». Они открыли дорогу для создания стабильных глайдерных отражателей, глайдерных дубликаторов, ружей и осцилляторов с различными периодами и различных преобразователей из глайдеров в ортогональные корабли и обратно, помимо прочего.
В частности, из дорожек для Гершелей оказалось возможным создать осциллятор с произвольным периодом больше 60. Я не буду демонстрировать в этой статье способ это сделать, так как в доказательстве омнипериодичности участвует другой, более простой механизм создания осцилляторов с произвольным периодом. В своё время, однако, это оставило всего 21 неоткрытый период.
1997-2002. Конец эпохи частых открытий.
Здесь мы увидим всего одно новое имя: Ахим Фламменкамп. Немецкий математик, проведший довольно большую перепись результатов случайных первичных бульонов. Он не открыл новых периодов, но его осциллятор позволил Элкису найти новый период.
54P17.1 — осциллятор, открытый Дином Хикерсоном. Для бильярдного стола это очень большой период. 168P22.1 — хасслер, открытый Ноамом Элкисом.
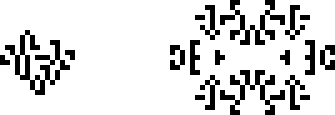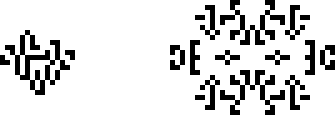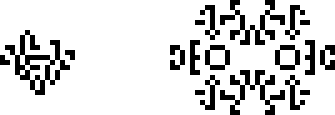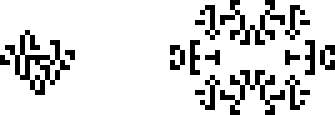
Ранее в статье упоминалось, что НОК-осцилляторы считались тривиальными. В какой-то момент отношение к ним изменилось, и в 1997 году мы видим пример открытия нового периода именно за счёт НОК-осциллятора. Ноам Элкис нашёл искрящий осциллятор с периодом 3 и поставил его рядом с осциллятором с периодом 11, найденным Ахимом Фламменкампом, получив осциллятор с периодом 33. С названием он тоже особо не заморачивался.

Сможете заметить единственную клетку, которая осциллирует с периодом 33?
Эпоху частых открытий завершают два осциллятора, найденные Элкисом в 2000 и 2002 годах, с периодами в 39 и 27, соответственно. С первым ему в этом ещё помог Давид Бакинэм.
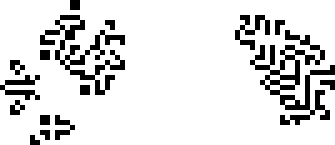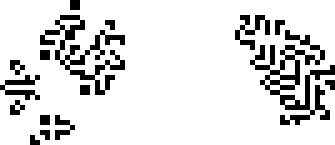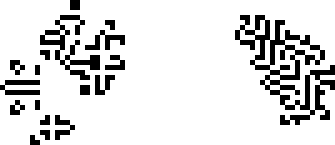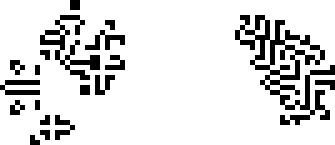
После 2002-го года мы не увидим ни одного нового периода аж до 2009-го года. Вероятно, это связано с отсутствием активного сообщества в это время.
2009 год. Начало новой эпохи.
В феврале 2009-го был зарегистрирован домен conwaylife.com. В то время на заглавной странице был только Java-апплет с эмуляцией игры «Жизнь», а также ссылки на форум и вики, которые живы и активно развиваются по сей день.
С притоком людей начали появляться и новые открытия. Николай Белюченко порадовал открытием осциллятора с периодом 37, а Маттиас Мерцених — с периодом 31.
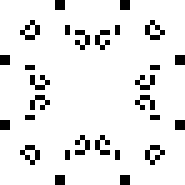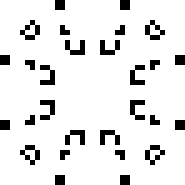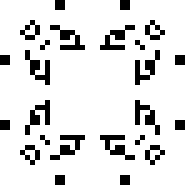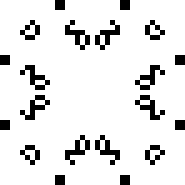
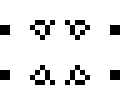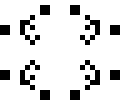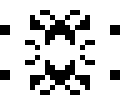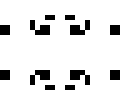
Осцилляторы с периодом 43 и выше — Снарковый цикл
В 2013 году, 25 апреля Майком Плейлом (Mike Playle) был найдена весьма значимая конфигурация — Снарк. Это — стабильный глайдерный отражатель с временем повторения 43. Это значит, что входящие глайдеры могут подаваться с любой задержкой между ними, начиная с 43 тиков, без изменений самой реакции (включая разрушительные). Открытие Снарка значительно расширило возможности инженерных конструкций в игре «Жизнь». Давайте же полюбуемся на него:
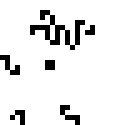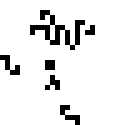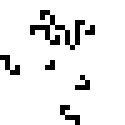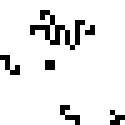
Четыре копии этого красавца могут быть расположены в углах квадрата, образуя замкнутый глайдерный цикл. Путём варьирования стороны квадрата можно изменять длину этого цикла. В частности, для любогоможно найти такое
, что произведение
:
-
Достаточно большое, чтобы Снарки не пересекались.
-
Делится на 8 (следствие того, что изменение расстояния между двумя парами Снарков на 1 меняет длину цикла на 8, и что период Снаркового цикла сам по себе имеет остаток 0 при делении на 8)
Затем, при условии, что, в этом цикле можно разместить
глайдеров, и получившаяся конфигурация будет осциллятором с периодом
. Вот пример для
:

Последние пять периодов
Итак, после открытия Снарка осталось всего 5 периодов, для которых на тот момент не было известно нетривиальных осцилляторов. Это 19, 23, 34, 38 и 41. Сообщество игры «Жизнь», конечно, занималось активным поиском осцилляторов с целью заполнить, наконец, эти пропуски. Росла вычислительная мощность компьютеров, программы для поиска дорабатывались, однако удача не улыбалась сообществу аж до 2019 года.
Давид Гильберт — осциллятор с периодом 23, найденный Лукой Оканиши на основе частичного осциллятора, найденного пользователем praosylen. Слово «частичный» означает, что конфигурация не является настоящим осциллятором, но очень близка к нему. Конкретно в данном примере, достаточно изменить всего одну клетку, чтобы начальная конфигурация совпала с результатом через 23 тика. Если зациклить визуализацию, невооружённым глазом нельзя будет даже заметить, что что-то идёт не так (у опытных энтузиастов глаз уже намётан и может заметить явные отклонения от типичного поведения конфигураций).
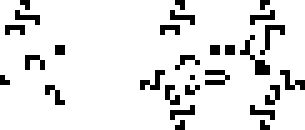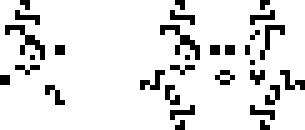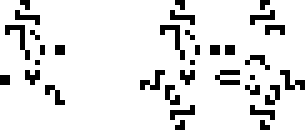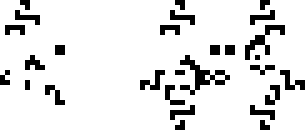
12 января 2022 года Давид Раучи нашёл осциллятор с периодом 38. Интересно, что фитиль, лежащий в основе этого осциллятора (фитиль — стабильная или периодическая линейно повторяющаяся конфигурация), был известен ещё в 2000 году. А вот катализатор стабилизирующий фитиль и состоящий из 3/4 светофора (конфигурация из 4 блинкеров) и пожирателя — не был. Вообще, этот катализатор оказался весьма универсальным и смог найти своё место в нескольких других конфигурациях. Сообщество было достаточно шокировано, что такой, казалось бы, простой катализатор не был найден так долго.

CatForce — программа, написанная Майклом Симкиным в 2015 году. Она работает, перебирая все возможные способы разместить маленькие стабильные конфигурации в ограниченной зоне и фильтруя те из них, которые приводят к восстановлению изначального состояния после реакции с активным регионом. В мае 2022-го Мичел Рилей доработал её, значительно увеличив скорость работы и добавив возможность поиска симметричных конфигураций. Это привело его к открытию 6 июля 2022 года нового (нетривиального) осциллятора с периодом 34.
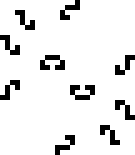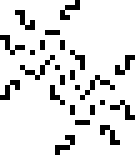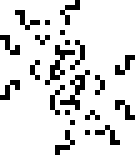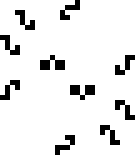
Спустя год, 14 июля 2023-го года, всё тот же Мичел Рилей, с помощью всё той же CatForce, смог найти криббэдж — осциллятор с периодом 19. Сообщество было просто в восторге. Но оставался ещё один период…
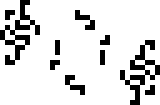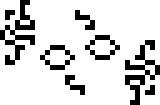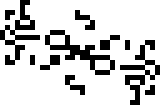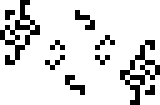
… И всего лишь неделей позже, Нико Браун обнаружил осциллятор с периодом 41. На этот раз это экземпляр зависимого цикла. В его основе лежит периодическая реакция, выпускающая глайдеры, которой, однако, нужно подкрепление в виде входящего потока глайдеров с тем же периодом. Отсюда и слово «зависимый». Совместить две таких реакции с правильным расстоянием между ними, образовав цикл с периодом 41 — уже дело техники.

Эпилог и полезные ссылки
Это было весьма длинное путешествие для сообщества, и оно, наконец, завершено. Одна из главных проблем игры «Жизнь» разрешена с утвердительным результатом. Кстати, сейчас идёт работа над статьёй, которая представит результат научному сообществу.
Сообщество игры «Жизнь» сейчас весьма активно. У нас есть форум, вики и сервер Discord (ссылки можно найти на https://conwaylife.com/). Идёт каталогизация объектов, полученных в результате поиска среди сотен квадриллионов начальных конфигураций. Строятся новые и новые инженерные конструкции, ищутся новые осцилляторы с целью минимизации размера. Стоит упомянуть и то, что активно исследуются и другие клеточные автоматы, как близкие к «Жизни», так и совсем непохожие на неё.

Недавно также была написана замечательная книга по игре «Жизнь». В ней последовательно описаны все аспекты, начиная от простейших конфигураций, и заканчивая грандиозными инженерными конструкциями, позволяющими эмулировать произвольные клеточные автоматы на бесконечном поле. В ней нет самых свежих результатов, в частности, омнипериодичности, но о них можно узнать, заглянув на вики. Кстати, книга бесплатно доступна в pdf-формате, а при желании можно заказать её печатный вариант на lulu.com. Очень рекомендую! Я сам, хоть и знал о многом из того, что описано в книге, с удовольствием её прочитал.
Спасибо за внимание!


