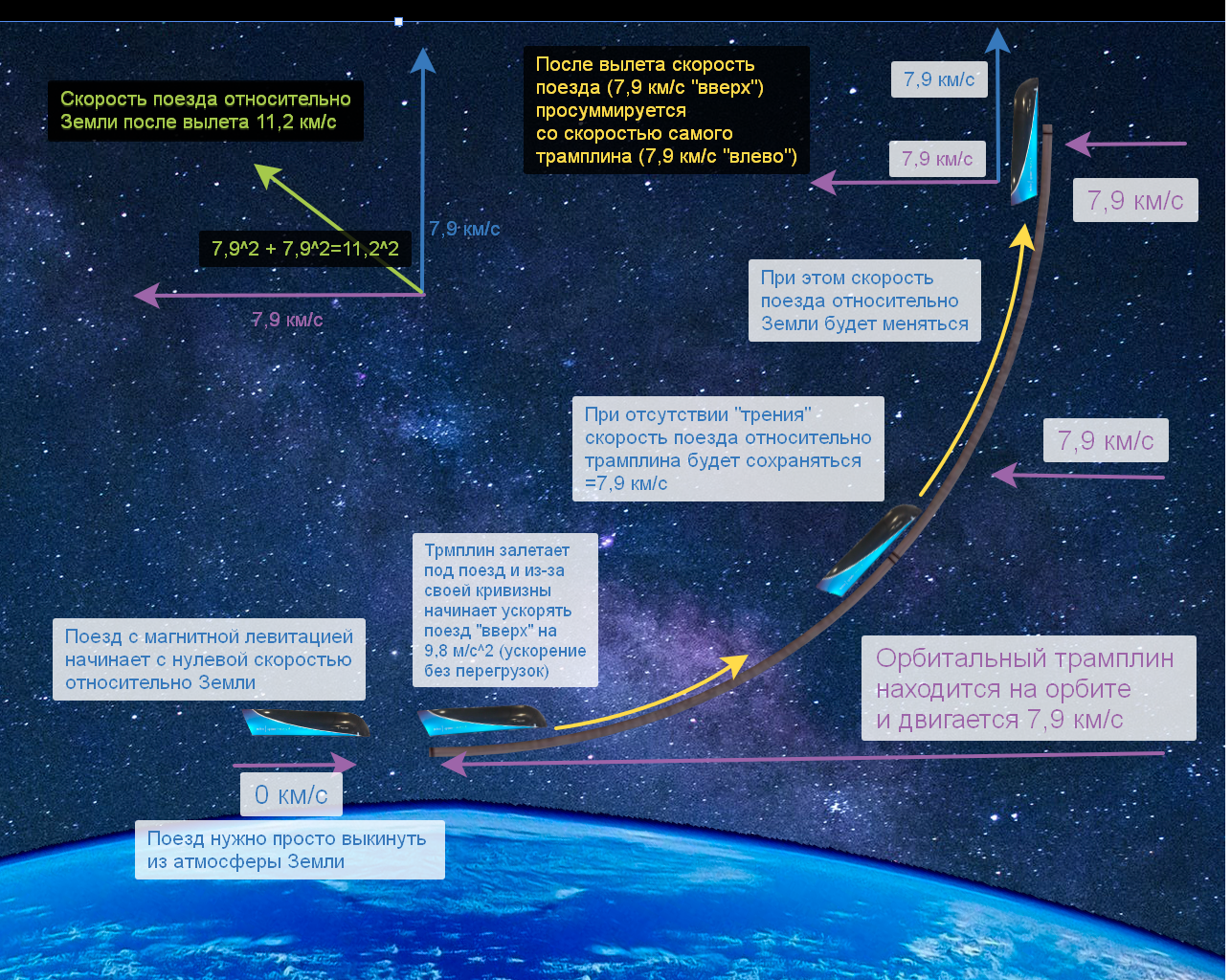
Принцип работы достаточно прост. Подбрасываем поезд на магнитной подушке вверх на высоту 400 км, для подъёма на такую высоту понадобится кинуть поезд вверх со скоростью ~1,7 км/с, если это делать с помощью обычной ракеты, то при удельном импульсе 3 500 м/с понадобится сжечь 650 кг топлива на каждую тонну полезной нагрузки, для сравнения: многоразовый Falcon 9 для вывода 1 тонны на орбиту сжигает 33 тонны топлива = в 507 раз больше.
Итак, подбрасываем поезд на высоту 400 км где он встречается с трамплином находящемся на орбите и двигающимся со скоростью 7,9 км/с. Трамплин геометрически является частью окружности (четверть в данном примере). При заезде под поезд, магниты поезда начинают отталкиваться от магнитов трамплина с ускорением 9,8 м/с, но из-за кривизны трамплина, поезд не может отлететь от трамплина, потому что, когда поезд ускоряется «вверх» на 10 м/с и поднимается на 5 метров выше — дорога тоже поднимается на 5 метров и, таким образом, поезд постоянно находится рядом с дорогой и постоянно ускоряется. При этом скорость самого поезда относительно трамплина всегда будет одинаковая, постоянные магниты по сути создают абсолютное скольжение с почти нулевым трением.
Математически, всё считается по формулам центробежной силы, как если бы мы привязали поезд верёвкой к центру и раскрутили до 7,9 км/с — центростремительную силу тут создают магниты, а центробежная сила создаётся кривизной трамплина. Кстати, это бы работало и с обычной машиной на колёсах.
Движение по такой дороге на обычной машине ничем бы не отличалось от движения по Земле, кривизна дороги будет создавать искусственную гравитацию, если для удобства восприятия не учитывать естественную гравитацию, то вы бы ощущали всё тоже самое что и при езде по Земле с гравитацией 9,8 м/с — вы бы заехали на дорогу со скоростью 7,9 км/с и выехали с дороги 7,9 км/с, с той лишь разницей, что это не вы ехали по дороге — это дорога ехала под вами.
Разумеется, речь идёт о передачи импульса (постоянные магниты создают почти абсолютно упругое столкновение, КПД больше 99,99%) — вы ускоряетесь = дорога тормозит, если вы отправляетесь только в один конец, и не собираетесь возвращаться — то вам придётся оплачивать импульс, который потеряла дорога, но… если вы просто собрались слетать на Луну на пару месяцев — то по возвращении обратно вам нужно будет тормозить и проделав всё то же самое, что и при ускорении, только в обратном порядке — вы вернёте импульс трамплину — и по сути, цена такой поездки будет около нуля.
Трамплин геометрически является четвертью круга, а если увеличить его до полукруга — то скорость вылета составит 16 км/с — это уже больше третьей космической и с такой скоростью можно лететь хоть на Юпитер, хоть на Альфа Центавру.
Вы только представьте… Вы едете на мотоцикле и обращаете свой взгляд в небеса, а вверху не просто небо — там Земля, но вы не чувствуете её притяжение — вы чувствуете силу толкающую вас в другую сторону — от Земли… И вы понимаете, что вы покидаете Землю… Может быть на пару месяцев… А может и навсегда.
Самый эффективный угол поворота — это 90 градусов, и если вы летите не на Луну, а на Марс, то вам нужен еще один трамплин — на орбите Солнца. Сначала вылетаете с орбиты Земли (11,2 км/с), и переходите на орбиту Солнца — где вас встретит второй трамплин, находящийся на точно такой же высоте как и вы (150 млн.км от Солнца) и двигающийся ровно с такой же скоростью как и вы (30 км/с) — но его орбита ретрограда — вы двигаетесь по 30 км/с лоб в лоб.
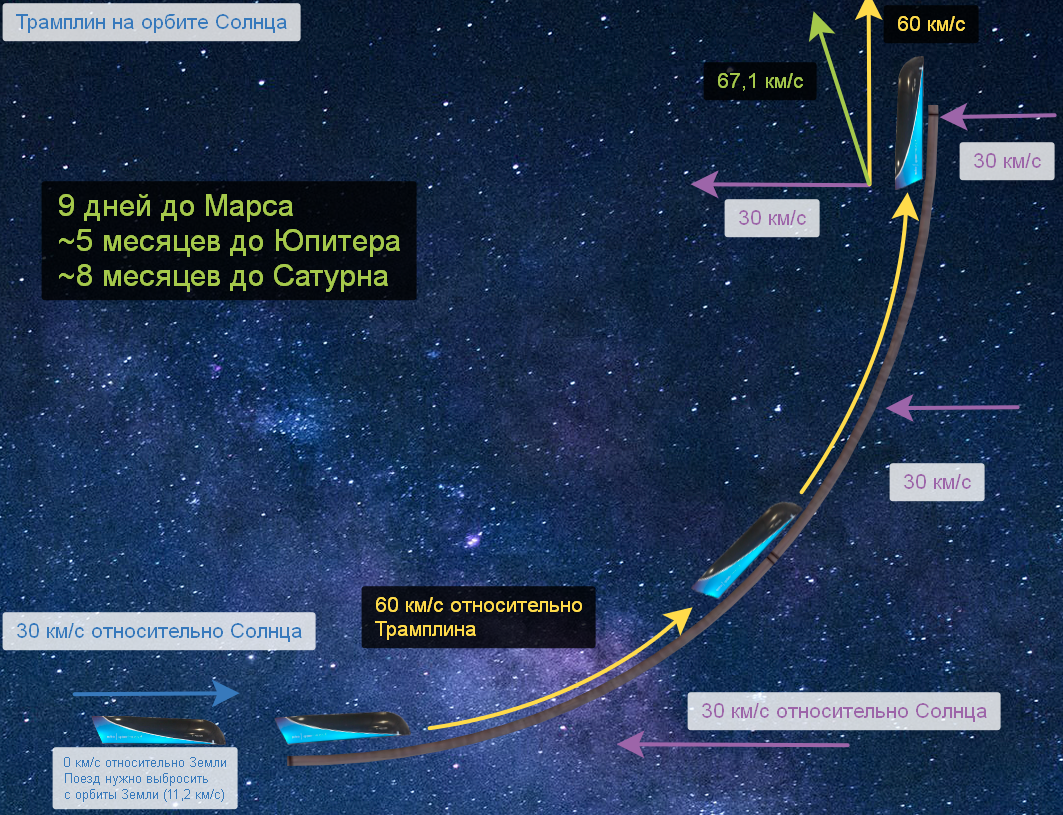
Если ускоряться без перегрузок, то радиус Солнечного трамплина составит 360 000 километров (от Земли до Луны 400 000 км), длина 565 200 км, а время поворота составит ~2,5 часа. Масса магнитов на таком трамплине будет около миллиона тонн (мировые запасы неодима около 100 миллионов тонн) — в принципе, ресурсов всей Земли хватит на постройку таких дорог около каждой планеты. А главная фишка таких дорог заключается даже не в том, что они позволяют добраться до Марса за неделю, а в просто фантастической пропускной способности — транспорт двигается по дороге со скоростью 216 000 км/ч, если мы возьмём массу транспорта 1 тонну (обычная легковушка 1,2-1,5 тонны) и представим плотный поток (на каждые 20 метров 1 машина), то за секунду дорога будет запускать по 3 000 машин, а за месяц грузовой поток составит 7,8 миллиарда тонн. Как дорога массой около миллиона тонн может ускорить за месяц 7,8 миллиарда тонн? — односторонняя никак — нужен поток в 2 стороны — либо одновременный, либо по очереди. Всего одна такая дорога сможет отправить на Марс всё население Земли за 1 месяц. Да и вообще, сегодня во всём мире на кораблях перевозят 11 миллиардов тонн грузов ЗА ГОД!!!, а дорога может поменять 7,8 млрд тонн грузов за месяц.
Из-за постоянного движения планет, круглый год такая дорога работать не сможет, стартовые окна возникают не каждый месяц, на Марс каждые 780 дней (2,16 лет), на Юпитер раз в 1,2 года (чем дальше, тем чаще). Съехать с дороги можно в любой точке, поэтому доступен огромный набор траекторий полёта и стартовые окна будут длиться по несколько месяцев.
Масса магнитов
Теперь давайте примерно прикинем массу магнитов и представим сколько нужно магнитов чтобы подвешать стоячий поезд над Землёй. Общую массу поезда возьмём 1 тонну (масса магнитов + масса всего остального = 1 тонна)
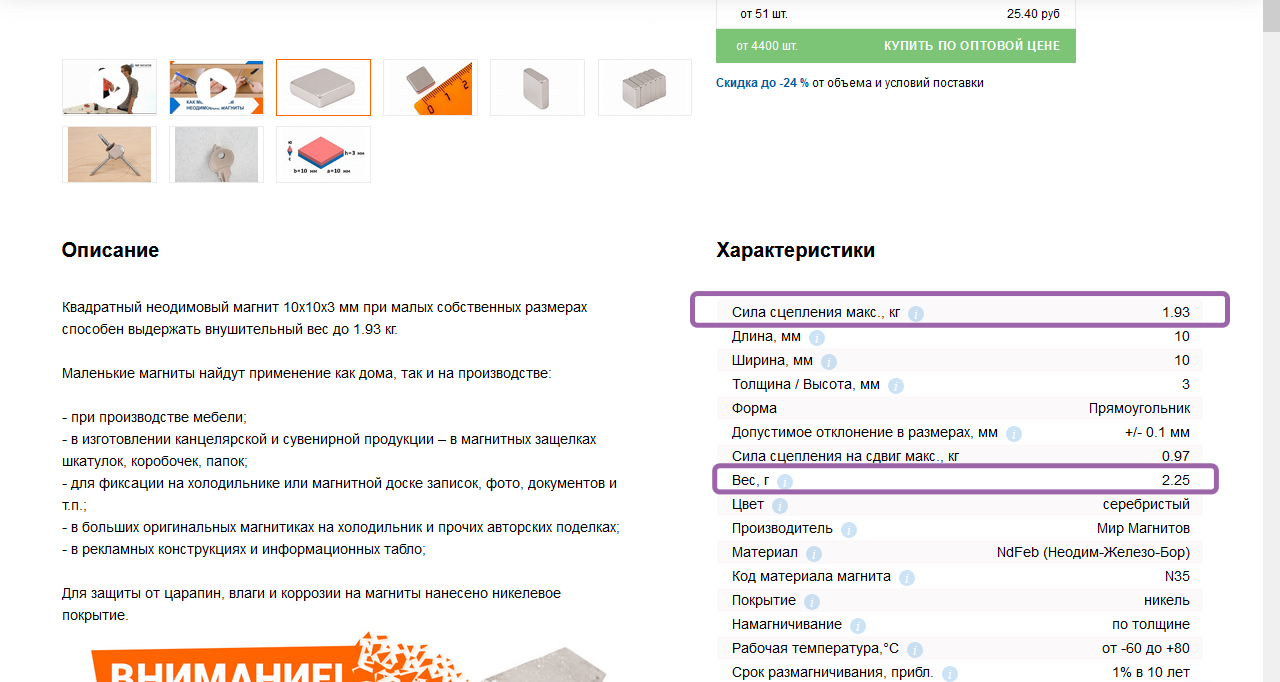
Неодимовый магнит массой 2,25 грамма может держать 1,93 килограмма при ускорении 9,8 м/с — в 857 раз больше своей массы (сила притяжения к «железу» = сила притяжения 2-х одинаковых магнитов = сила отталкивания магнитов), но это при полном соприкосновении и с нулевым зазором, при отдалении сила взаимодействия уменьшается, закон кулона говорит нам, что при увеличении расстояния в 2 раза сила уменьшается в 4 раза, хотя это для точечных зарядов и в случае с диполями по формулам всё сильно усложняется, но по результату разница небольшая.
Масса дороги
Сколько будет весить 1 метр дороги? — Зависит от длины поезда, если длина поезда будет 5 метров — то и 6 кг магнитов под поездом нужно расположить на 5 метров длины, а в каждом метре дороги будет 1,2 килограмма магнитов, но если длина поезда будет 10 метров, то эти же 6 кг магнитов нужно распределить уже на 10 метров, а в каждом метре будет уже 0,6 кг магнитов, т.е. при увеличении длины поезда (или магнитной платформы поезда) в 2 раза, масса каждого метра дороги уменьшается в 2 раза.
Если выложить вышеупомянутые магниты (10 мм каждый) в 1 линию то её длина составит 26,38 метров и каждый метр такой дороги весил бы 230 грамм, но «ехать» по одному рельсу не удобно и давайте возьмем более реалистичный вариант и разложим магниты в 5 линий и округлим длину до 5 метров. Т.е. 5 рельс на дороге и у поезда магниты тоже выстроены в 5 рядов. Итак, при длине поезда 5 метров масса дороги составит 1,2 кг на метр. Какая нагрузка будет на дорогу массой 1,2 кг на метр по которой «едет» поезд массой тонну?- Зависит от скорости с которой «едет» этот поезд, и в случае с орбитальной околоземной дорогой, скорость поезда будет составлять ~7 900 метров в секунду, если масса дороги 1,2 кг*метр, то масса 7 900 метров составит 9,5 тонн и поезд будет отталкивать от этих 9,5 тонн, ускоряясь на 9,8 м/с за секунду, т.е. при увеличении скорости — нагрузка на дорогу уменьшается, вернее общая нагрузка сохраняется — суммарно на всю дорогу действует нагрузка, как будто по ней едет поезд с ускорением 9,8 м/с, но локальная нагрузка уменьшается — поезд за секунду проходит 7 900 метров и каждый отдельный метр дороги ускоряет его на 0,0012 м/с
.
Общая масса околоземной дороги составит ~12 000 тонн — как 29 МКС (по 417 тонн), при этом масса дороги от её длины никак не зависит, если уменьшить длину дороги в 2 раза (уменьшить радиус), то увеличится и её кривизна = ускорение поезда увеличится в 2 раза = понадобится в 2 раза больше магнитов на каждый метр и масса дороги составит те же 12 000 тонн (длина уменьшается в 2 раза=плотность магнитов увеличивается в 2 раза), но при этом поезду тоже понадобится в 2 раза больше магнитов, а он в отличии от дороги короче не стал и масса магнитов у поезда увеличится в 2 раза (до 1,2% при прошлых параметрах). Т.е. от общей длины дороги — зависит масса магнитов у поезда, а от длины поезда — зависит общая масса магнитов у дороги. Поэтому с точки зрения эффективности, укорачивать дорогу смысла нет, но с точки зрения строительства — одно дело строить на орбите дорогу длиной 10 000 километров и другое дело строить дорогу длиной 2 000 км (перегрузки 5G +1G сама гравитация, о ней чуть позже, пока представим что гравитации нет).
Уменьшить массу дороги можно увеличив силу магнитов (я брал не самый сильный, да и зазор 3 мм достаточно большой), либо увеличив длину «поезда» в 2 раза до 10 метров = масса дороги 6 000 тонн и ещё уменьшить массу самого поезда в 10 раз до 100 килограмм и тогда масса дороги составит уже 600 тонн как 1,5 МКС — для грузового варианта очень не плохо, особенно с учётом максимального грузопотока, при 60 км/с было 7,8 миллиардов тонн в месяц, а при 8 км/с будет 1,04 миллиарда тонн, ещё мы уменьшили массу грузов в 10 раз — тогда 104 миллиона тонн, но в случае с Луной не нужно будет ждать стартовые окна и дорога сможет работать круглые сутки, значит 1,25 миллиарда тонн в год— по моему ни плохо для дороги массой 600 тонн (или 1200 тонн для 2-х направлений). А если строить дорогу только для грузов, то тогда и перегрузки можно увеличить хоть до 20G (масса магнитов в поезде 12%), тогда общая длина дороги составит 500 километров (~320 км радиус). Что такое 20G? — ну возьмите помидорку и поставьте на неё сверху еще 20 таких же помидорок, если за 40 секунд помидорка не деформируется — значит помидорка выдерживает 20G – очень много чего выдержит 20G на протяжении 40 секунд.
Ёмкость аккумулятора и режим ускорителя.
Дорога сама по себе является лишь аккумулятором импульса который при ускорении грузов «разряжается» = дорога теряет скорость = уменьшается высота её орбиты. И заряд этого аккумулятора равен высоте, которую может потерять дорога не влетев в атмосферу Земли. При начальной высоте 500 км и спуске до 300 км (высота орбиты МКС 400 км) «заряд» дороги получится ~1 500 000 Дж на каждый килограмм её массы, чтобы отправить 1 кг на Луну нужно 64 000 000 Дж = в 42,7 раза больше = дорога может отправить 2,3% своей массы в 1 сторону и аккумулятор как бы «разрядится», самый эффективный способ «зарядки» — это принять ровно такую же массу грузов с Луны, но это подразумевает что на Луне уже есть заводы, отели, фермы и т.п., и для начала колонизации Луны такой способ не очень подходит. (отправлять грузы с Земли на Марс и другие планеты аккумулятор тоже может, но очень сильно падает грузопоток и придётся достраивать аккумулятор до полукруга, гораздо эффективней будет сначала отправить всё что нужно на орбиту Луны, и от туда лететь на Марс на большой ракете (от Луны до Марса ~0,7 км/с)).
Чтобы превратить аккумулятор в ускоритель с нуля, для начальной колонизации Луны с нуля, когда там ничего нет — понадобится источник импульса.
Один из наилучших способов накачки аккумулятора импульсом — это ускорять его с помощью солнечного паруса. У света есть импульс и при падении+отражении света на зеркало — зеркало будет получать ускорение.

Японский солнечный парус IKAROS запущенный 3 июня 2010 года.
Сегодня, главным недостатком солнечных парусов является то, что они дают очень мало импульса и ускоряют очень долго (спутник на солнечном парусе будет «ускорятся» до Луны несколько месяцев), и наличие аккумулятора импульса частично решает эту проблему, потому что с точки зрения груза — полёт до Луны будет длится 5 дней, при этом с таким аккумулятором, получается, что солнечный парус сможет ускорять грузы с 0 км/с до 11,2 км/с (обычный солнечный парус может работать только уже находясь на орбите = двигается 8 км/с), а разгон до 8 км/с — это 97% топлива. К тому же при наличии аккумулятора срок службы солнечного паруса становится почти бесконечным.
Сколько импульса даёт солнечный парус
Продолжение следует
Постараюсь дописать следующую часть в течении недели.


