Авторская квантовая теория гравитации

3 Янв в 03:06

Данная статья продолжает изложение новых методов решения задач математики и физики, не поддававшихся решению в течении столетий.

В настоящее время Википедия считает, что квантовая гравитация — это направление исследований в теоретической физике, целью которого является квантовое описание гравитационного взаимодействия (и, в случае успеха, — объединение гравитации с остальными тремя фундаментальными взаимодействиями, описываемыми Стандартной моделью, то есть построение так называемой «теории всего»). Поэтому для подтверждения создания теории всего я просто обязан показать как выглядит закон Ньютона в квантово-релятивистской формулировке.

В предыдущей статье было указано, что наряду с пространственной решётчатой функцией (ПРФ)существует временная решётчатая функция (ВРФ). Каждая из них при разложении в ряд по степеням постоянной тонкой структуры порождает фундаментальные взаимодействия принципиально разного типа: пространственные и временные. Для получения временной решётчатой функции прямое использование идеи решётки является слишком тривиальным. Это связано с тем, что в случае пространства перемещения в решётке возможны в любом направлении, а в случае времени перемещения в решётке возможны только в одном направлении.

Поэтому в качестве «замка» на перемещения в запрещённых направлениях целесообразно использовать определение производной нормального распределения по времени, но без перехода к пределу. Пусть $\mathbb{R}\left(t\right)$ есть ВРФ на единичном интервале $\left[-T/2, T/2\right]$ при $\tau=\sigma$ и :

$\mathbb{R}\left(t\right)=\frac{1}{\tau\sqrt{2\pi}}\sum_{i=-\infty}^{\infty}\left[ \exp\left(-\frac{1}{2}\left(\frac{t+T/4-iT}{\tau}\right)^{2}\right)-\exp\left(-\frac{1}{2}\left(\frac{t-T/4-iT}{\tau}\right)^{2}\right)\right].$

Последовательно вычитая численно синусы из $\mathbb{R}\left(t\right)$ , можно показать, что её аппроксимация имеет следующий вид:

$A\left(t\right)=\sum_{k=0}^{\infty}\left(-1\right)^{k+1}a_{k} \sin\left(2\pi\left(2k+1\right)t\right).$

Для определения значений коэффициентов $a_{k}$ используем уравнений с различными значениями :

$\sum_{i=0}^{k}\left(-1\right)^{i}a_{i} \sin\left(\frac{2i+1}{2l+1}\frac{2\pi}{4}\right) = \mathbb{R}\left(\frac{1}{4\left(2l+1\right)}\right).$

Несмотря на то, что в решётчатом пространстве нет производной по времени как таковой, разработанный ещё Эйлером в 1768 году метод предиктор-корректор для задачи Коши, требуется применять и для решения вышеуказанных уравнений. Следствия этого будут обсуждены в следующих статьях.

Учитывая, что $A\left(1/4\right)$ численно равно

$2\left(\mathbb{R}_{max}\left(\tau\right)+\mathbb{R}_{min}\left(\tau\right)\right)\alpha\left(\tau\right),$

это уравнение можно записать в следующем виде:

$\alpha_{eff}\left(t,\tau\right) = -\alpha \sin\left(2\pi t\right) + \sum_{k=1}^{\infty}\left(-1\right)^{k+1}\sqrt{\left(2k+1\right)}\alpha^{2((2k+1)^{2})} \sin\left(2\pi\left(2k+1\right)t\right).$

Появление ПТС в разложении $\mathbb{R}\left(t\right)$ обусловлено периодичностью времени. Периодичность времени описывается антисимметричной функцией от . $\mathbb{R}\left(t\right)$ также является гипераналитической функцией. Наконец, следует отметить, что каждый член разложения соответствует более высокой частоте не чисто формально, а реально, т.е. каждая амплитуда умножается на квадратный корень из показателя частоты.

Таким образом, разложение $\mathbb{R}\left(t\right)$ в пространстве Фурье существует!

Квантово-релятивистская формулировка закона Кулона

Очевидно, что первый член разложения соответствует закону Кулона:

$\vec{\mathbf{F}}_{12}=-\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r_{12}^2} \cdot \frac{\vec{r}_{12}}{r_{12}},$

где — первый заряд, — второй заряд, $r_{12}$ — расстояние между зарядами.

Исходя из определения для постоянной тонкой структуры, закон Кулона можно записать в квантово-релятивистской формулировке:

$\vec{\mathbf{F}}_{12}=-\alpha \hbar c\cdot\frac{ \frac{q_1}{e } \frac{q_2}{e } } {r_{12}^2} \cdot \frac{\vec{r}_{12}}{r_{12}}.$

На мой взгляд наиболее принципиальное отличие новой формулировки состоит в переходе от размерных зарядов к их безразмерному количеству.

Квантово-релятивистская формулировка закона Ньютона

Уже в 1922 году чикагский физик Артур Лунн (Arthur C. Lunn) рассмотрел возможную связь гравитационной постоянной с постоянной тонкой структуры $\alpha$ посредством соотношени.

$\frac{G {m_e}^2}{e^2} = \frac{\alpha^{17}}{2048 \pi^6},$

где $m_{e}$ — масса электрона, — заряд электрона.

Учитывая, что в то время погрешности измерения входивших в формулу констант оставляли желать лучшего, на этот явный путь к теории всего не обратили внимания.

Пусть $m_{pa}$ есть присоединённая масса протона — космологическая константа, вводимая вместо гравитационной постоянной . Её значение можно выбрать таким образом, чтобы теоретическое значением $m_{pa}$ давало экспериментальное значение :

$G=\sqrt{3}\alpha^{18}\frac{\hbar c}{m_{pa}^{2}}.$

Полученная формула раскрывает неизвестный ранее квантово-релятивистский статус самого закона тяготения Ньютона. В этом и есть смысл априорной теории всего, основанной на уравнениях Максвелла. Дело в том, что произведение $\hbar\times c$ , входящее в $\alpha$ и , сохраняется только при одновременном преобразовании $c \rightarrow\infty$ и $\hbar\rightarrow0$ согласно принципу соответствия. Таким образом, говорить об одностороннем уточнении закона тяготения Ньютона, сделанном в общей теории относительности, оказывается в принципе неправильно.

На основе данных, приведённых ниже:

$\alpha=7.297 352 566 4(17) $\times 10^{-3}$ $\ G=6.674 08(31) \times 10^{-11}м^{3}с^{-2}кг^{-1}$ $\ c=299 792 458 м/с,$ $\hbar=1.054 571 800(13) $\times 10^{-34}$ Дж c$

(взяты из Википедии 14.03.2020), получаем:

$m_{pa}=1.68082*10^{-27} кг.$

Таким образом, значение $m_{pa}$ всего на 9 электронных масс превышает массу протона $m_{p}$ и может считаться достоверным.

Это означает, что в среднем Вселенная состоит из »очень горячего водорода». Или, что в среднем тяготение действует только на атомы как на электрические диполи, причём в момент когда они антипараллельны друг другу (см. рисунок ). Поэтому сила тяготения не экранируется. Ввиду этого в принципе существует гравитационное расщепление спектральных линий, но измерить его экспериментально вряд ли удастся.

Уточнённый закон Ньютона получает квантово-релятивистский статус:

$\vec{F}_{12}=\sqrt{3}\alpha^{18}\hbar c\frac{ \frac{M_1}{m_{pa1}}\frac{M_2}{m_{pa2}} } {r_{12}^2} \cdot \frac{\vec{r}_{12}}{r_{12}},$

где $r_{12}$ — расстояние между телами 1 и 2.

— масса тела 1,

— масса тела 2.

Таким образом, $m_{pa1}$ и $m_{pa2}$ являются поправками, которые переводят инертные массы в правильные гравитационные массы.

С другой стороны, указанные значения могут быть вычислены. В качестве примера оценки $m_{pa}$ можно считать, что эта величина включает массу протона $m_{p}$ и массу электрона $m_{e}$ . Кроме того необходимо включить поправку на разность между массой нейтрона и массой протона с коэффициентом $\delta$ — долей нейтронов на один протон, которая составляет десятые для звёзд и единицы для планет. Также надо вычесть энергию связи связанных нуклонов, которая различна для звёзд и планет.

Наконец, для звёзд надо добавить массу фотонов в звёздах (фотонам, испытывающим множество столкновений на пути от ядра звезды до её поверхности, может потребоваться около миллиона лет чтобы покинуть звезду). Однако, это задача астрофизиков.

По перпендикуляру к диполю поле равно нулю

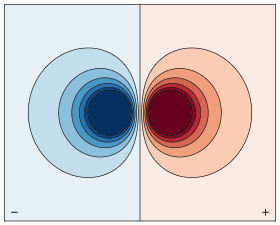
Наконец, последняя деталь «гравитационного взаимодействия» диполей в том, что они взаимодействуют направленно по оси перпендикулярной диполю. Именно это и обеспечивает отсутствие экранирования.

Источник

Авторская квантовая теория гравитации

Читайте также

Паблик ВКонтакте

Последние посты