Угол аберрации соответствует такому направлению зрительной трубы, что квант света от Источника, попавший в её входное отверстие или линзу, будет двигаться именно вдоль оси трубы по мере перемещения Приёмника и жёстко прикреплённой к нему трубы, и в конце концов будет им принят. Этот угол оказывается различным в классической и релятивистской механике. Вывод формулы релятивистской аберрации света подробно изложен, например, в статье на стр.338, но начинается он на стр.334, и естественно значительный объём там занимает вывод преобразований Лоренца.
Однако сама суть релятивистской аберрации света связана с лоренцевым сокращением масштабов Приёмника, имеет наглядную интерпретацию и вполне понятна даже школьникам. Этот же метод применялся автором для вывода формулы доплер-эффекта. Все нужные обозначения указаны на рис.1 и там все события отражены в системе отсчёта (СО) Источника. Приёмник движется вправо со скоростью V от точки B к точке C. Явление аберрации, как видно на схеме слева, состоит в том, что видимое направление на Источник будет отклонено от фактического в сторону движения Приёмника, т.е. Источник будет наблюдаться Приёмником (в СО Источника) не под углом α, а под углом γ параллельно линии AB.
На рисунке фронт первой волны (отмечен цифрой 1 в кружочке) принимается в точке B. Расположение в этот момент фронта следующей (второй) волны отмечено цифрой 2 в кружочке. Расстояние между фронтами равна длине λи волны Источника.
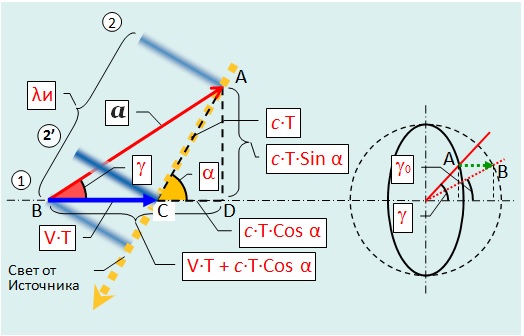
Рис.1
Приёмник примет фронт 2-й волны (отмеченной 2′ в кружочке) в точке C. Фронты перпендикулярны лучу света. От приёма 1-го фронта до приёма 2-го пройдёт время Т. Расстояния: BC = V∙T, AC = c∙T, AB = a, откуда получаем (1) и (2).
Разделив уравнение (1) на (2) получим выражение (3), откуда, разделив числитель и знаменатель на c∙T, получим искомую формулу аберрации света (4), где β = V/c. И тут угол аберрации именно таков, как и должен быть в классической механике.
Но так как в системе Источника Приёмник движется, то, следовательно, является в ней сжатым по Лоренцу вдоль траектории, как на рис.1 справа. Однако в собственной СО Приёмника этот эллипсоид будет восприниматься как сфера вследствие такого же изменения эталонов длины. В таком случае и собственный угол аберрации изменится, как показано красной пунктирной линией. Точка A пересечения лучом аберрации эллипсоида перейдёт по зелёной пунктирной стрелке в точку B пересечения им сферы. Соответственно, тангенс угла γ0 станет меньше тангенса угла γ в отношении лоренцева сокращения согласно (5). Умножая выражение в формуле классической аберрации на этот коэффициент получим искомую формулу релятивистской аберрации (6). Точно такая же формула для угла аберрации приводится в курсе теоретической физики Ландау и Лифшица, «Теория поля», §5, ф-ла (5,5). Но там она выведена посредством пересчёта координат ИСО движущейся в 4-х мерном абстрактном пространстве Минковского. А здесь вывод проведён согласно евклидовой геометрии в ньютоновом пространстве и реальная физика релятивизма видна явно в явлении лоренцева сокращения движущихся тел.
Вид звёздного неба из субсветовой ракеты
Интересно феномены теории относительности (ТО) проиллюстрировать картинкой звёздного неба, которую в иллюминаторы увидела бы команда звездолёта при скорости близкой к световой. Звёзды условно считаются неподвижными. Описание того, что будет видно из звездолёта при скорости 0,8660254 световой опубликовано проф. С.М.Рытовым, но практически без формул, в статье. Можно убедиться, что для этой скорости его и мои расчёты совпадают. Отмечу, что азимуты в статье Рытова считаются не от направления движения ракеты к цели, а в обратном порядке. Эти же вопросы рассматриваются в лекциях Фейнмана.
В данной статье приводится наглядный вывод всех необходимых формул и графиков в широком диапазоне скоростей, включая и 0,866. Задачу будем решать в системе отсчёта Источника света. Наблюдатель (изображён смайликом) движется налево со скоростью V и принимает свет от неподвижных Источников, находящихся под разными углами α (азимутами) относительно его вектора скорости.
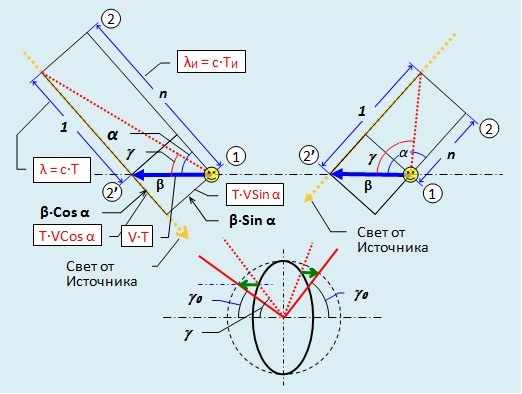
Рис.2
На левом верхнем чертеже рис.2 свет принимается от звёзд с азимутами менее 90°. Позиция, когда был принят фронт первой волны отмечена цифрой 1 в кружочке. Расположение в этот момент фронта следующей (второй) волны отмечено цифрой 2 в кружочке. Расстояние между фронтами, т.е. длина «λи» волны Источника указана рядом красным текстом в рамке, где «Ти» длительность периода волны. Приёмник примет фронт 2-й волны в позиции отмеченной 2′ в кружочке. Фронты перпендикулярны лучу света. От приёма 1-го фронта до приёма 2-го пройдёт время Т, а длина принятой волны λ=с∙Т. Все эти отношения изображены на рисунке красным шрифтом в рамках. Угол аберрации обозначен γ, а луч аберрации изображён красной пунктирной линией. Мы перейдём к безразмерным координатам, разделив все длины на с∙Т. Тогда скорость звездолёта выразится отношением V/c = β. А «λи» следует заменить на n = λи / λ = Ти / Т.
На правом верхнем чертеже рис.2 показана схема при приёме света от звёзд в задней полусфере относительно звездолёта уже в безразмерных величинах. Формулы (7) и (8) следуют непосредственно из чертежа. Как известно, отношения между замедленным собственным временем Т0 в системе движущегося Наблюдателя и временем процессов Т в системе Источника выражаются формулой (9). Применяя её к (8) получаем (10). Поскольку в любой СО скорость света численно одинакова, для Источника и для Наблюдателя длина волны света и период связаны формулами (11). Подставляя их в (10) получим (12).
На рис.2 угол аберрации γ показан в системе Источника. А в системе Наблюдателя ему соответствует угол γ0, который вычисляется по ранее выведенной формуле (6).
Для построения зависимости угла аберрации и доплеровского сдвига от скорости звездолёта нам понадобятся формулы (6) и (12).
Для сравнения покажем на рис.3, как эти графики выглядят без релятивизма, например, для звуковых волн, где «с» просто скорость звука. Видим, что минимальный угол аберрации равен половине исходного азимута, а минимальная длина принятой спереди волны равна половине излученной. Так и должно быть.
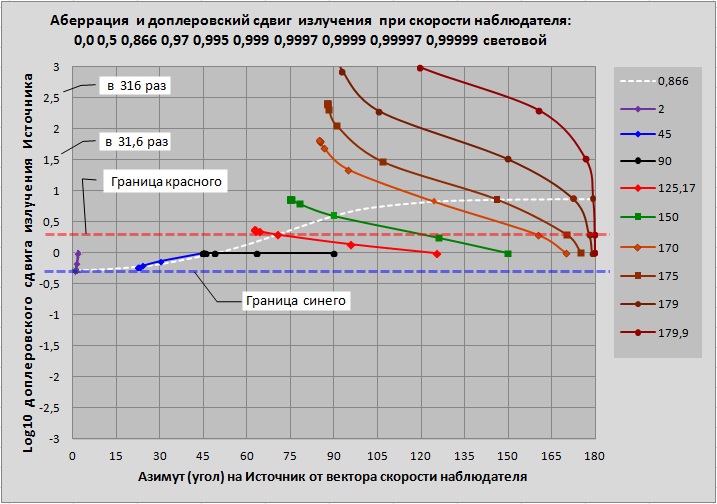
Рис.3
Графики с релятивистскими поправками показаны на рис.4. Белая штриховая кривая соединяет точки соответствующие скорости 0,866 световой.
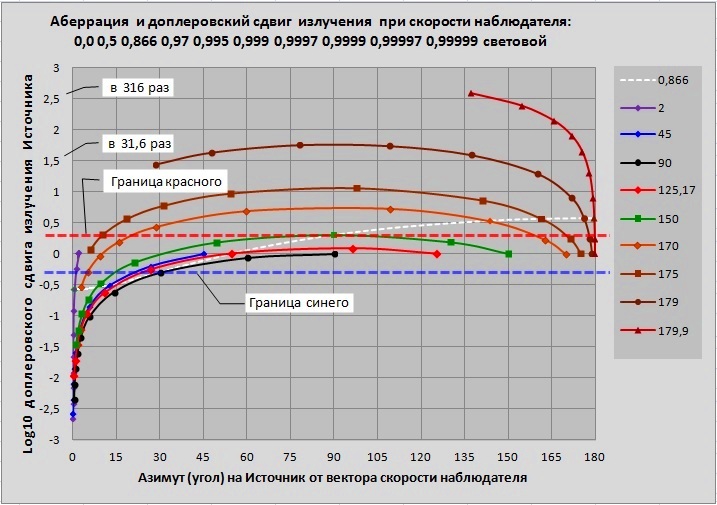
Рис.4
Итак, что же увидит звездолётчик при скоростях близких к световой?
Звёзды в передней полусфере уже при «небольшой» скорости звездолёта посинеют, а из задней полусферы покраснеют, и даже выйдут за пределы видимого диапазона, отмеченного «границами синего и красного». Но с ростом скорости, все звёзды со всего небосклона соберутся в колечко прямо по курсу и будут двигаться к его центру по мере ускорения звездолёта. И в этом колечке опять станут видимы звёзды из задней полусферы небосклона. Внешние края колечка будут окрашены в красные, а внутренние преимущественно в синие цвета. В центре будет тёмное пятно, так как там спектры всех звёзд перейдут в область невидимого ультрафиолета.
Впрочем, возможно станут видимыми участки их спектра инфракрасного излучения. В боковые иллюминаторы возможно станут наблюдаемы расположенные позади объекты излучающие в рентгеновском диапазоне волн. В общем, прямо по курсу звездолётчики увидят картинку похожую на рис.5.
Рис.5
Фотографии субсветового объекта
Чтобы избежать смазывания картинки и искажений формы при фотографировании объекта важно, чтобы он не успел существенно переместиться за время выдержки. Для субсветового объекта это означает, что свет от любых точек объекта за время выдержки должен проходить расстояние существенно меньшее деталей объекта. И значит лучи несущие изображение всех точек объекта должны одновременно попасть в объектив за время выдержки. В идеале, лучи с изображением от точек А, Б и В исходного объекта должны находиться в пределах одного волнового фронта, обозначенного цифрой 3 на рис.6.I.
Для этого свет от точки Б должен отправиться в момент, когда она находилась в точке Г, чтобы оказаться в одном волновом фронте (3 в кружочке) одновременно с изображением от точки А. Чтобы одновременно сюда попал и свет от точки В, он должен был отправиться, когда она находилась в точке Е. Таким образом видимое изображение реального объекта АБВ будет образовано точками АГЕ. Нас интересует изменение визуальной длины L’ объекта относительно его реальной длины L или собственной длины L0 и угол φ наклона элементов перпендикулярных движению в плоскости образованной векторами оси зрения и скорости.
Рис.6
Из чертежа на рис.6.I очевидно:
Таким образом, исходный объект с размерами L0 и h0 в собственных координатах, связанных с реальными размерами L и h соотношением (16) и h = h0 и приведенный на рис.6.III (белый), на снимке будет выглядеть в соответствии с формулами (17) и (20) как там же красный. Графики функций угла φ (подписаны «Угл») из формулы (20) и отношения L’/L0 из формулы (17) показаны на рис.7 для скоростей объекта 0,5 0,866 0,95 и 0,99 относительно световой.
Рис.7
Следует иметь в виду, что по оси абсцисс отложен угол ϑ = (180-α°) характеризующий направление зрения на встречный объект. На рис.6.II показано, что для объекта следующего прямолинейно на расстоянии S от наблюдателя, угловой размер длины объекта L видимого под углом ϑ будет, вследствие перспективы, сжат пропорционально sin ϑ, а расстояние до объекта будет в 1/sin ϑ больше, чем S, когда он будет виден в зените (или по траверсу), так что визуально размер объекта будет во столько же раз меньше, а в итоге в (sin ϑ)² раз. Именно такие размеры длины объекта отражают кривые «Прп» относительно видимой собственной длины объекта, когда бы он неподвижно находился в зените на той же траектории. В зените же (или по траверсу) движущийся объект имеет видимую длину соответственно его лоренцеву сокращению.
Кривая «Прп 0» соответствует длинам объекта, если бы он неподвижно находился в точках траектории соответствующих азимутам наблюдения. Обратим внимание, что передняя сторона объекта (фас) будет видна только при азимутах меньших, чем при которых соответствующая кривая «Угл» пересекает линию «Фас». При бо́льших углах, вследствие скоса фасада назад, он будет заслонён нижней (или ближайшей к наблюдателю) стороной объекта. Например, в направлении по траверсу (или в зените) у движущихся объектов в рассматриваемом диапазоне скоростей (0,5–0,99) углы φ наклона переднего фасада назад лежат в диапазоне от 25° до 45°, но этого не будет видно. Зато с азимута 90° и далее становится видна задняя сторона объекта. Сначала без деталей, так как несущие изображение лучи скользят вдоль стенки, а затем и с деталями видимыми под данным азимутом, но видимое изображение задних перпендикулярных поверхностей будет растянуто (в плоскости траектории и наблюдателя) в 1/cos φ раз относительно размера у неподвижного объекта в том же месте.
