
Современные города с высоты птичьего полета напоминают клетчатый плед, с множеством пересекающихся улиц, переулков, проспектов, аллей и бульваров. Каждый из этих элементов градостроения имеет свое название, направление и какие-то примечательные особенности, позволяющие нам лучше ориентироваться в урбанистском муравейнике. Самым коротким путем между точками А и В, естественно, является прямая, но в городской среде это не всегда реализуемый вариант. Тогда возникает вопрос — каким маршрутом нужно идти, чтобы быстрее добраться до места назначения? Ученые из Массачусетского технологического института (США) установили, что человеческий мозг, в отличие от GPS-навигатора, плохо справляется с расчетами кратчайшего пути. Это часто приводит к тому, что человек выбирает путь, направление которого указывает в сторону точки назначения, даже если сам путь оказывается длиннее. Какие данные удалось собрать в ходе исследования, какой алгоритм лежит в основе такой странной работы мозга, и чем его можно объяснить? Ответы на эти вопросы мы найдем в докладе ученых. Пошли Поехали.
Основа исследования
Часто можно наблюдать довольно забавную картину: новый район, уложены красивые тротуары, по бокам зеленеют газоны, цветут клумбы. Одним словом — красота. Но, то тут, то там виднеются вытоптанные дорожки через газон. С одной стороны в этом есть логика, ибо «новый» маршрут, созданный жильцами, короче того, что создавался градостроителями. С другой стороны, порой такие срезы настолько малы, что экономия времени в случае их использования варьируется в пределах нескольких секунд.
Еще одним любопытным наблюдением является то, как мы иногда выбираем путь к месту, где ранее не были. Мы заранее изучаем карту и видим, что место назначения расположено, допустим, на вершине своеобразного прямоугольного треугольника. Однако кратчайший путь (гипотенуза) пролегает через дворы, а там и площадки, и бюветы, и парковки с сотнями машин, и какие-то лавки с овощами. Посему мы выбираем более длинный маршрут по катетам, зато без полосы препятствий.
Конечно, далеко не все люди так делают, но некоторые все же предпочитают ходить по длинному, но понятному пути, нежели петлять дворами и закоулками, так как они могут по их же словам «заблудиться в трех соснах» (буквально).
Хотя планирование пути человека может по большей степени быть оптимальным, все же наблюдаются систематические отклонения от кратчайшего пути. Почему так происходит, ученые прошлого так и не смогли понять. Авторы рассматриваемого нами сегодня исследования предположили, что подобные отклонения возникают из-за вычислительного механизма мозга, являющего общим для всех людей. Если гипотеза верна, значит этот процесс можно структурировать, вычислить все его составляющие, и сформировать универсальный алгоритм.
Для любого исследования подобного характера необходимы данные, и чем больше — тем лучше. Однако в лабораторных условиях люди часто полагаются на принцип приблизительной (ограниченной) рациональности, согласно которому люди используют приблизительные эвристики* планирования для максимизации своих целей, ограничивая при этом субъективные затраты. Другими словами, в процессе принятия решения человек испытывает ряд трудностей, связанных с когнитивными ограничениями, нехваткой времени и/или ресурсов. В результате принятые решения нельзя назвать полностью рациональными.
Эвристики* — в данном контексте это мысленные сокращения, облегчающие когнитивную нагрузку при принятии решения (например, метод проб и ошибок).
В «полевых» условиях подобные затраты могут быть сочетанием умственных и физических усилий. Например, умственные затраты на планирование маршрута связаны с физическими затратами на перемещение. Ранее уже проводили исследования данного феномена, однако методика их проведения, а также малая выборка данных не дали полного понимания того, как именно человек выбирает маршрут.
В данном же труде ученые собрали данные о передвижении 14380 пешеходов из Бостона и Сан-Франциско, что дало в результате 552478 пешеходных путей. Ученые также отмечают, что большинство полученных маршрутов отличалось от предлагаемых Google Maps, что указывает на минимальное вмешательство, вносимое траекториями, сгенерированными не человеком, а машиной.
Результаты исследования
Первым делом была проведена оценка путей на основе расстояния. В первой аппроксимации рассматривался способ формализовать стоимость пути как равную его расстоянию:

где P — путь между исходной точкой и местом назначения, который состоит из череды сегментов улиц S1, S2 и т.д., а li обозначает пешее расстояние одного сегмента Si.
Данная модель отражает мотивацию человека сокращать свой путь, что является центральным элементом планирования маршрута. Однако некоторые исследования показали, что люди часто отклоняются от кратчайшего пути, несмотря на его выгодность.
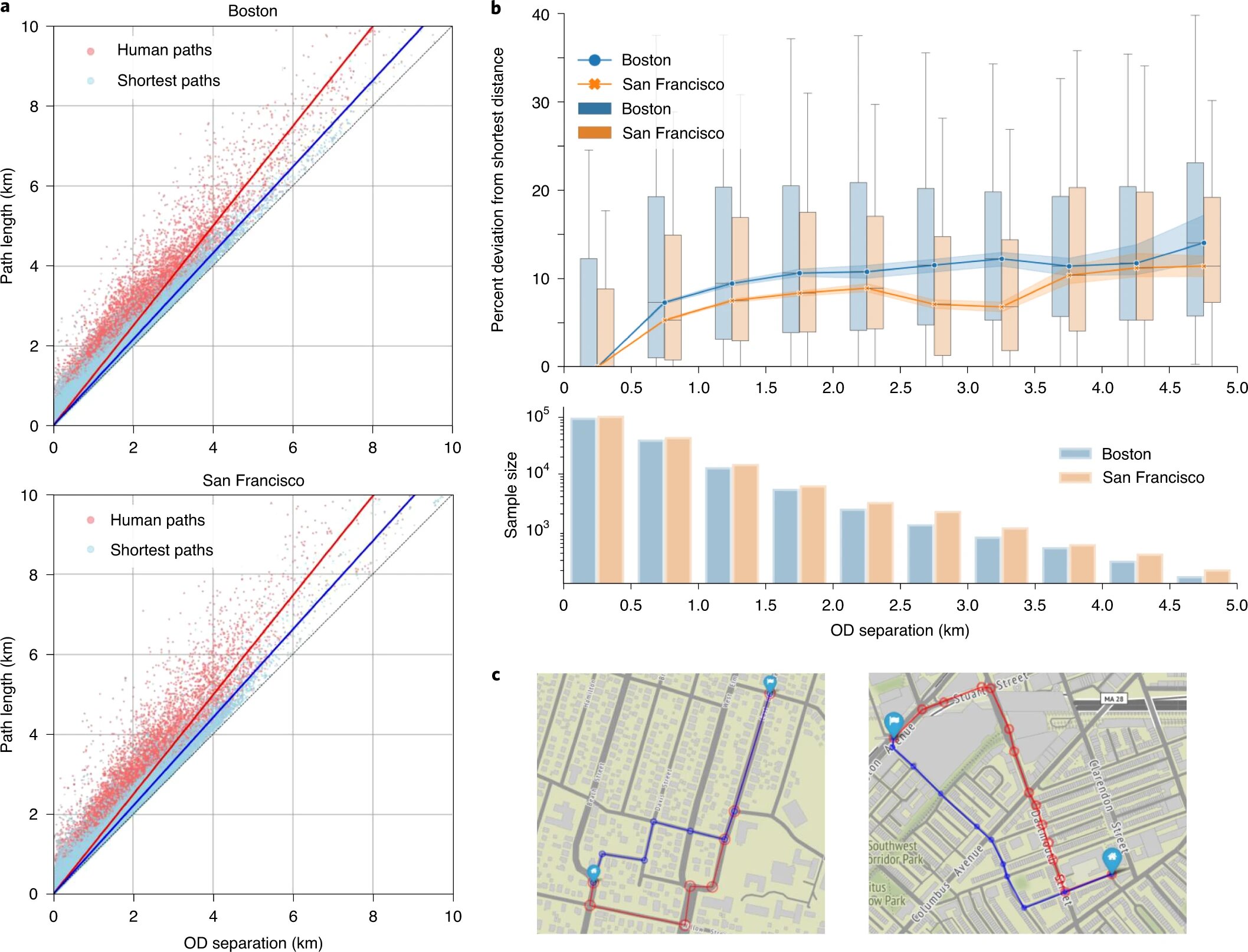
Изображение №1
На графике 1a видно, что пути из набора данных всегда были длиннее, чем пути с кратчайшим расстоянием, рассчитанным с помощью стандартного алгоритма Дейкстры.
Тенденция отклоняться от кратчайшего пути увеличивается с увеличением расстояния между исходной точкой и пунктом назначения (1b), что может быть связано с возрастающей сложностью оценки относительно более длинных путей в соответствии с принципом ограниченной рациональности. Любопытно, что большая доля отклонений наблюдается на маршрутах в 1 км, затем отклонения становятся реже.
Наблюдаемое возрастающее отклонение от кратчайшего пути может возникать из-за неуверенности человека в длине участков улицы, что приводит к накоплению ошибок с течением времени. Формально этот процесс можно описать следующим образом:

где функция стоимости c(li) получается путем применения логнормально распределенного случайного шума к исходной длине li участка улицы.
Использование логнормального распределения для моделирования неопределенности при оценке длины улицы мотивировано законом Вебера-Фехнера*.
Закон Вебера-Фехнера* — интенсивность ощущения чего-либо прямо пропорциональна логарифму интенсивности раздражителя.
Количество сегментов улиц в функции стоимости имеет тенденцию к увеличению с увеличением евклидова расстояния, разделяющего исходную и конечную точки маршрута. Следовательно, отклонение от кратчайшего расстояния имеет тенденцию накапливаться по мере увеличения расстояния между исходной точкой и пунктом назначения, что и наблюдается при анализе данных.
Ученые отмечают, что разработанная модель предсказывает, что выбор пути будет симметричным, т.е. доступные пути ранжируются в одном и том же порядке предпочтения независимо от направления движения, что может не соответствовать действительности.
Асимметрия навигации была продемонстрирована в лабораторных условиях в ходе предыдущих исследований. Теория навигации по прямой видимости предсказывает асимметричные маршруты и предполагает, что люди движутся по прямой линии обзора в желаемом направлении и, когда их обзор затруднен, устанавливают новую линию.
Эмпирические данные в области нейробиологии и психологии также предполагают, что нейронные и ментальные репрезентации пространства и направления могут приводить к асимметрии (к примеру, основанная на ориентирах навигация).
Ярким примером асимметрии пути является неодинаковая оценка расстояния от дома до парковки и от парковки до дома. Другими словами, оценка меняется в зависимости от того, где находится исходная точка пути, и где находится место назначения («What Do Misestimations and Asymmetries in Spatial Judgment Indicate About Spatial Representation?»).
Если асимметричные маршруты присутствуют в маршрутах испытуемых (чьи данные используются в исследовании), они будут искажать стохастическую модель минимизации расстояния, являющуюся основным фактором, влияющим на формирование пешеходных путей.
Чтобы проверить наличие/отсутствие асимметрии, ученые сначала проверили выбор асимметричных путей у одного человека, неоднократно посещающего любые два места в любом порядке. Если такая асимметрия на индивидуальном уровне присутствует, она может возникнуть из-за когнитивной эвристики стоимости, используемой для оценки траекторий, которая зависит от направления, или из-за стохастичности оценки расстояния с последующим запоминанием запланированного маршрута.
Затем, чтобы устранить неоднозначность этих двух сценариев, была выполнена проверка асимметрии в повторяющихся путях, сгруппированных по разным пешеходам. Такая асимметрия указала бы на постоянную планирования пути, которая не может быть объяснена стохастической оценкой, и, следовательно, может быть отнесена к общей эвристике стоимости, зависящей от направления.
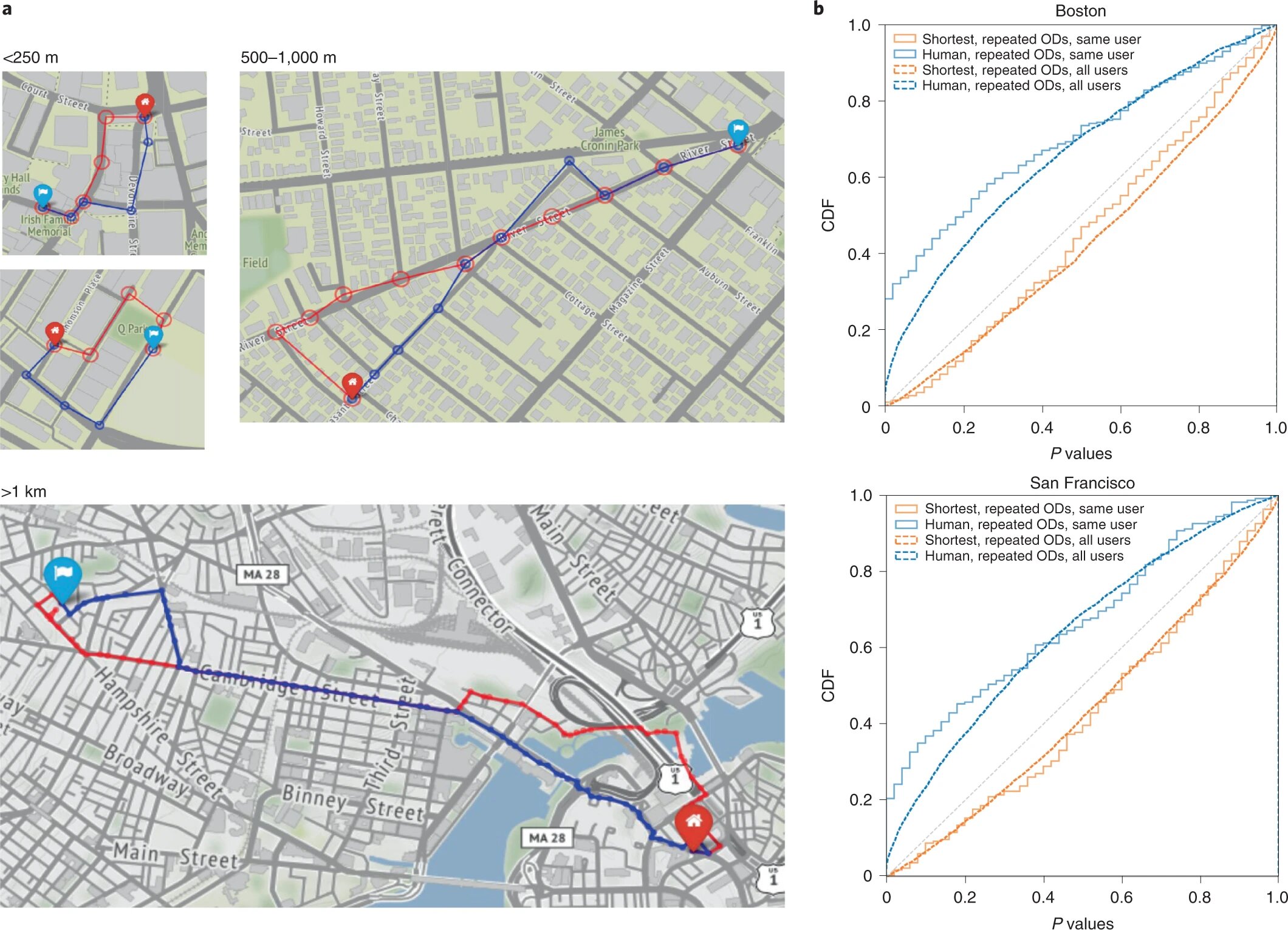
Изображение №2
На изображениях выше показаны результаты статистических тестов асимметрии на индивидуальном и на совокупном уровне. Результаты этих тестов показывают наличие асимметрии на обоих уровнях. Из этого следует, что асимметрия является постоянной составляющей пешей навигации в условиях города.
Дополнительным объяснением асимметрии навигации человека может быть теория «начального прямого сегмента» маршрута, выдвинутая Бейленсоном в его труде «The initial segment strategy: A heuristic for route selection».
Если человек действительно предпочитает в начале своего пути выбирать прямой участок маршрута, то последние будут длиннее, чем в случае с кратчайшим вариантом пути. Однако в реальности же начальный сегмент пути оказался короче, чем в кратчайшем маршруте (судя по данным). Следовательно, данная теория не может служить объяснением асимметрии.
Учитывая это, авторы исследования выдвинули собственную теорию, основанную на векторах, которые часто наблюдаются в навигации диких животных. Созданная векторная модель навигации отражена в стоимости выбранного пути, зависящей от углового отклонения участка улицы по отношению к пункту назначения:
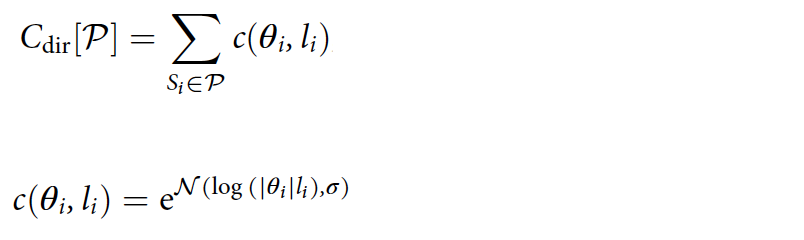
где θi∈[−π, π] представляет собой угол между касательной к пути на участке улицы Si и прямой линией до пункта назначения (изображение №3).
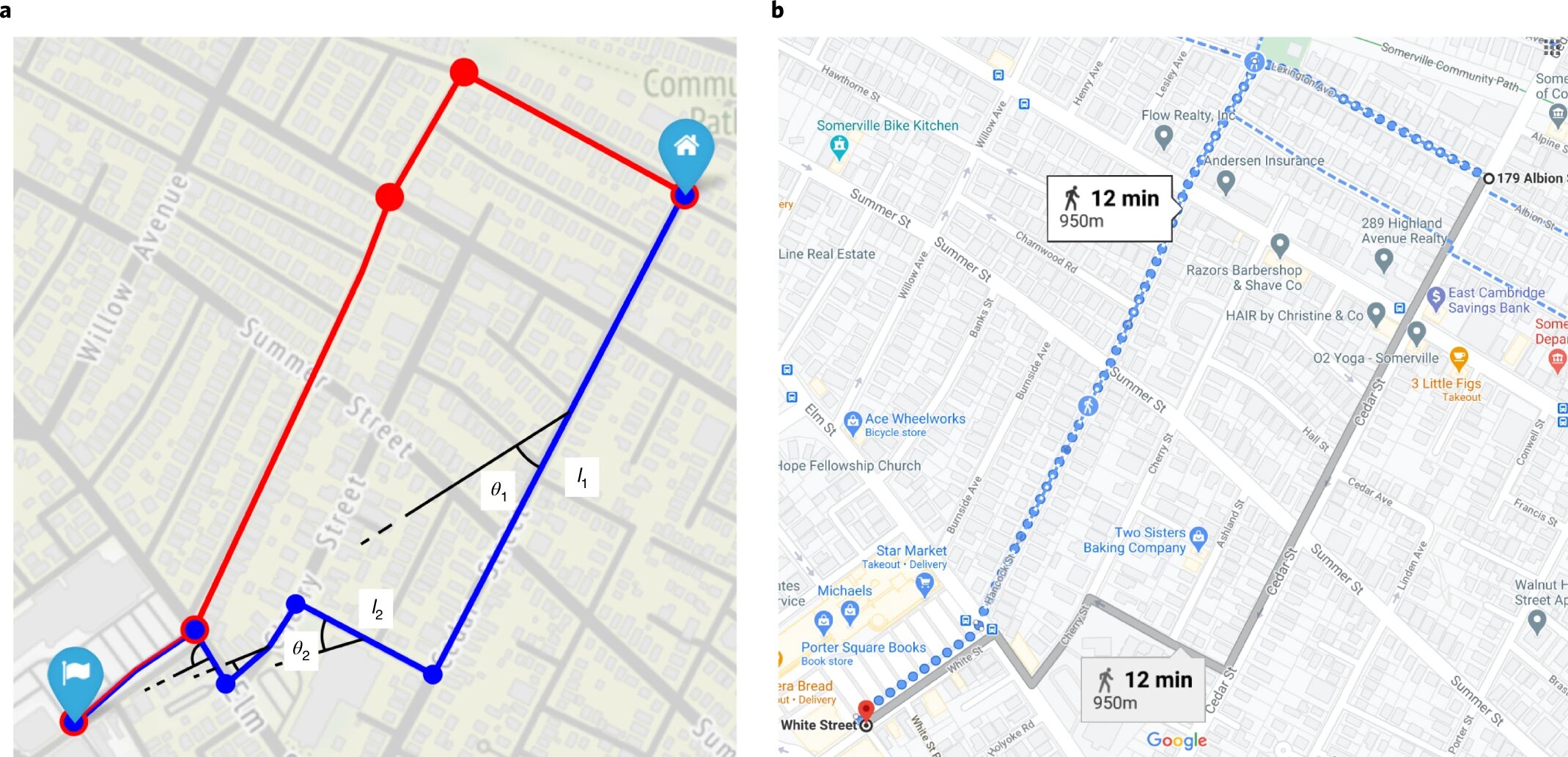
Изображение №3
В примере на 3a модель минимизации расстояния, использующая уравнение №1, больше склоняется к синему маршруту (для которого Σli = 935 м), а не красному (Σli = 938 м).
Но вот векторная модель предпочитает так называемый самый точный путь, то есть путь который более точно указывает на пункт назначения. В таком случае красный маршрут (Σ∣θi∣li = 400 м) преобладает над синим (Σ∣θi∣li = 516 м).
Поскольку угловые отклонения сегментов улиц в этой модели зависят от направления, оценка стоимости пути может измениться, если его направление поменять местами. Следовательно, векторная навигация может объяснить асимметрию, наблюдаемую в собранных данных.
Итого имеется две модели, описывающие процесс выбора пути: модель минимизации расстояния и векторная модель. Чтобы проверить, какая из них преобладает в реальных случаях ученые провели сравнительный анализ.
Все маршруты были сгруппированы по значениям расстояний между исходной точкой и пунктом назначения с шагом в 50 метров. Далее была проведена оценка наиболее вероятных параметров для минимизации расстояния и для векторной навигации в каждом из сегментов. Также была измерена доля путей в каждом сегменте, для которых векторная модель имела более высокую точечную вероятность, чем модель стохастической минимизации. Значение выше 50% означают более высокую вероятность того, что задействована именно векторная модель.
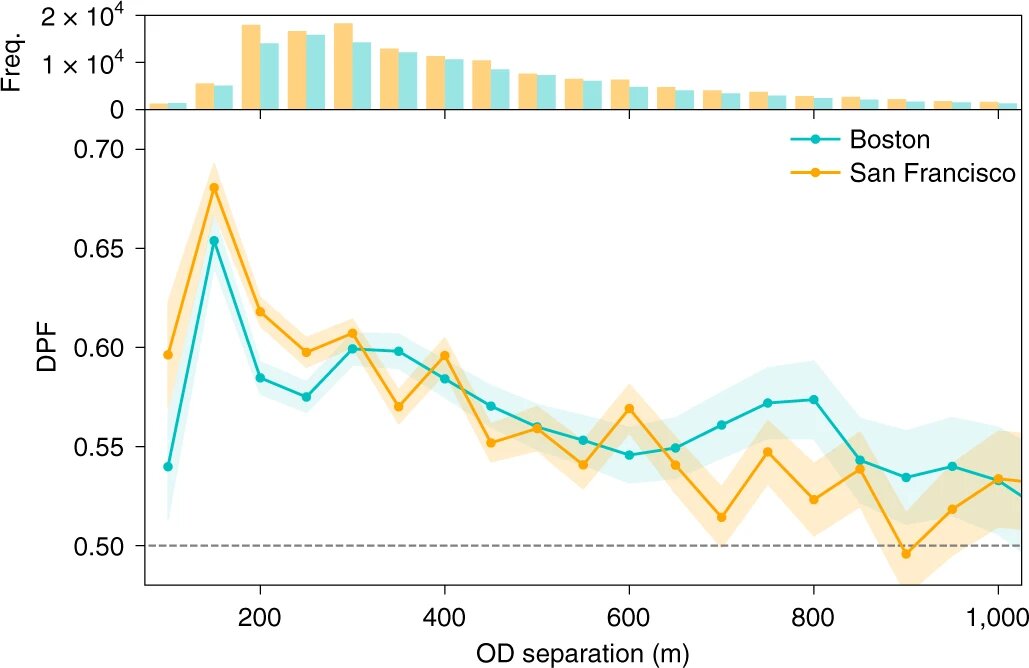
Изображение №4
На графике выше видно, что для и в Бостоне, и в Сан-Франциско преобладала векторная модель. Это свидетельствует о наличии некоего метакогнитивного умственного вычислительного процесса, который в ходе определения оптимального маршрута пытается сбалансировать умственные и физические затраты на его преодоление.
По мере увеличения длины запланированного пути люди, вероятно, переходят от относительно простой стратегии оптимизации направления к оптимизации расстояния для экономии физических усилий и времени в пути.
Для более подробного ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
В данном труде ученые провели анализ того, как человек выбирает оптимальный для себя маршрут при пешем перемещении по городу. Если исключить помощь карт и электронных навигаторов, то результаты выглядят достаточно любопытно. Анализ маршрутов более 14000 человек показал, что людям крайне сложно действовать по принципу «кратчайшего пути». Вместо этого нам свойственно выбирать тот маршрут, который более точно указывает в сторону пункта назначения, посему модель, объясняющая это, и была названа векторной.
В случае с векторной моделью человек выбирает маршрут, который оказывается длиннее того, который предложил бы навигатор. Вероятным объяснением этого нелогичного (на первый взгляд) решения является достижение баланса между умственными и физическими затратами. Другими словами, мозг тратит меньше сил на вычисление идеального маршрута, посему и возникает более длинный путь, чтобы сохранить энергетический запас на другие мыслительные задачи.
Дополнительным фактором поддержки векторной модели являются исследования, показывающие, что активность мозга (особенно в гиппокампе), связанная с навигацией, основана на вычислении векторов. Подобная тактика сильно отличается от той, что можно наблюдать в работе машинных навигаторов, обладающих доступом к картам. Вполне логично, что в мозге нет детальной карты местности с указанием названий всех улиц, их длин, примечательных мест и т.д. Посему мозгу необходимо было адаптироваться.
Грубо говоря, вам нужно дойти до точки В, вы знаете, что она где-то на востоке (или справа, кому как угодно). Даже если путь, предполагающий поворот на запад, короче, мозг предпочтет идти по пути, который векторно указывает на пункт назначения, т.е. на восток.
Данное исследование лишний раз показывает насколько сложен мозг человека, и как сильно его принципы работы отличаются от принципов работы вычислительной техники. Наш мозг часто вынужден идти на компромиссы с самим собой, чтобы мы могли достичь своей цели. Порой его решения кажутся нелогичными или неэффективными, особенно в сравнении с электронными эквивалентами. Однако несовершенность — это именно то, что делает нас людьми.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. 🙂
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?


