Действенная технология SAT-решателей может сработать с печально известной гипотезой Коллатца. Однако шансы на это не слишком велики.

В последние несколько лет Марийн Хиюл использовал технологию компьютеризированных поисков доказательств под названием «SAT-решатель» (SAT от «satisfiability», то есть, «удовлетворяемость»), чтобы покорить впечатляющий список математических задач. Пифагоровы тройки в 2016 году, число Шура 5 в 2017, а недавно и гипотеза Келлера в седьмом измерении, о чём мы не так давно писали в статье «Компьютерный поиск помог разобраться с 90-летней математической задачей«.
Однако теперь Хиюл, специалист по информатике из университета Карнеги-Меллона нацелился на ещё более амбициозную цель: гипотеза Коллатца, которую многие считают наиболее сложной из открытых задач в математике (и при этом, возможно, наиболее простой по формулировке). Другие математики, узнавая от меня о том, что Хиюл делает такую попытку, относились к этому с недоверием.
«Не вижу, как можно решить эту задачу полностью при помощи SAT-решателя», — сказал Томас Хейлс из Питтсбургского университета, ведущий специалист в области компьютерных доказательств. Эта технология, по сути, помогает математикам решать задачи – у некоторых из которых бывает бесконечное количество вариантов – превращая их в дискретные, конечные задачи.
Однако Хейлс, как и другие, опасался недооценить Хиюла. «Он очень хорошо умеет находить хитроумные способы формулировать задачи на языке SAT. У него это прекрасно получается».
Скотт Ааронсон из Техасского университета в Остине, совместо с Хиюлом работающий над гипотезой Коллатца, добавил: «Марийн – это человек с молотом, то есть, с SAT-решателем, и, вероятно, наиболее достойный носитель этого молота во всём мире. И он пробует применять его практически ко всему». Но лишь время покажет, получится ли у него превратить гипотезу Коллатца в гвоздь.
Решение по методу SAT требует переформулировки задач на понятном компьютерам языке, использующем пропозициональную логику, а потом подключения компьютеров, которые решают, есть ли способ сделать эти высказывания истинными. Вот простой пример.
Допустим, вы – родитель, пытающийся организовать присмотр за ребёнком. Одна из ваших нянь может работать всю неделю, кроме вторника и четверга. Другая – кроме вторника и пятницы. Третья – кроме четверга и пятницы. Вам нужно, чтобы с ребёнком сидели во вторник, четверг и пятницу. Можно ли этого добиться?
Один из способов проверить это – превратить ограничения нянь в формулу, и скормить её в SAT-решатель. Программа поищет способ так распределить дни между нянями, чтобы формула оказалась истинной, или «удовлетворяемой» – то есть, так, чтобы вы получили три нужных вам дня. В случае успеха такой способ будет существовать.
К сожалению, не сразу бывает понятно, как переформулировать многие из важнейших математических вопросов на язык SAT. Но иногда их можно перефразировать в виде вопросов, проверяемых на удовлетворяемость, неожиданными способами.
«Сложно предсказать, когда задачу можно будет свести к огромному, но конечному вычислению», — сказал Ааронсон.
Гипотеза Коллатца – один из тех вопросов в математике, которые сначала вообще не кажутся похожими на задачу с нянями. Она предлагает следующее: взять любое число (целое, ненулевое). Если оно нечётное, умножить его на 3 и добавить 1. Если чётное, поделить на 2. В итоге вы получите новое число. Примените к нему те же правила, и продолжайте. Гипотеза предсказывает, что вне зависимости от стартового числа, вы в итоге получите 1, после чего застрянете в цикле: 1, 4, 2, 1.
И, несмотря на то, что с этой гипотезой работают почти 100 лет, математики не приблизились к её доказательству.
Но это не остановило Хиюла. В 2018 они с Аронсоном – в то время будучи коллегами по университету – получили грант от Национального научного фонда на применение SAT-решателя к гипотезе Коллатца.
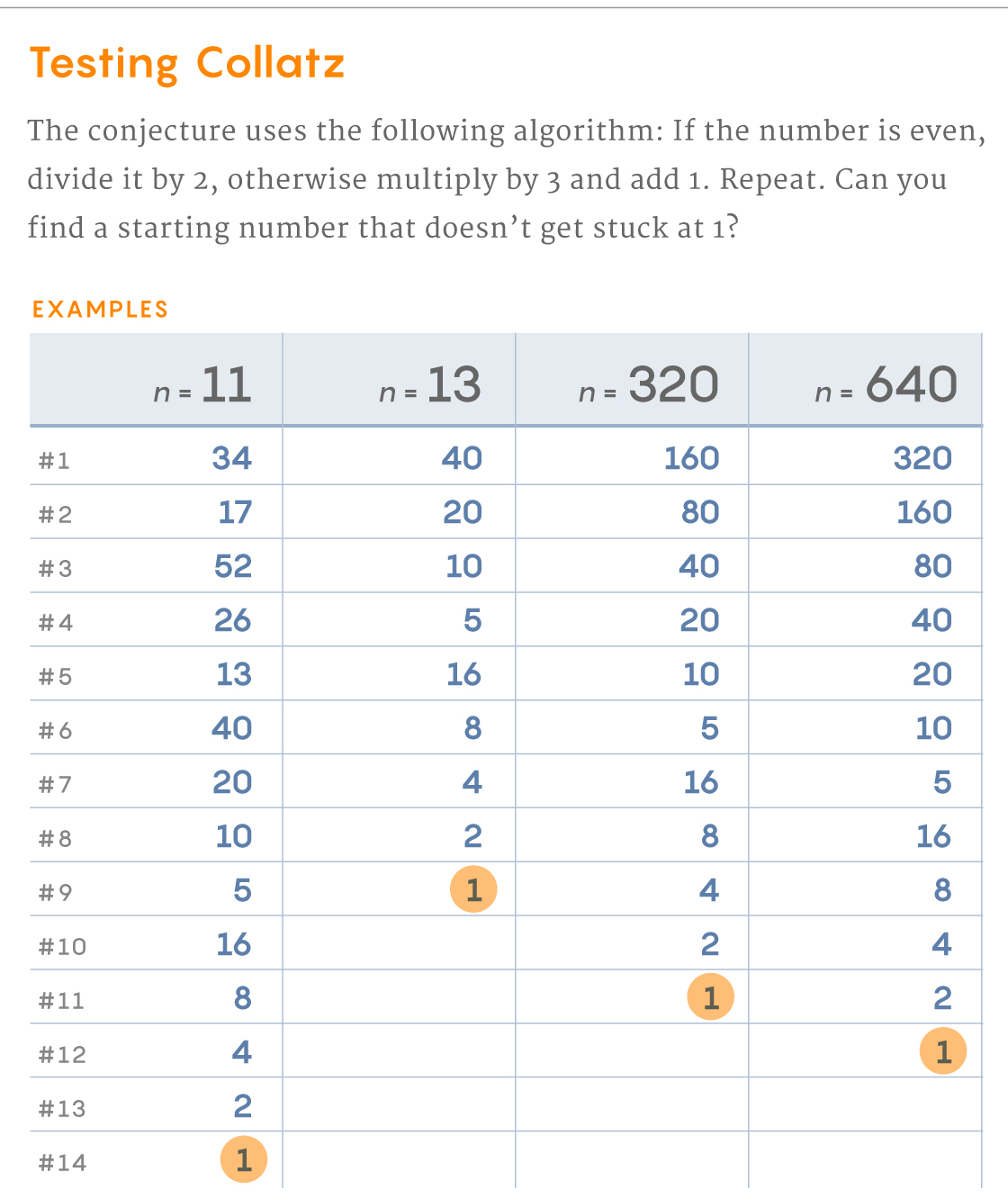
Возьмите любое число. Если оно нечётное, умножить его на 3 и добавить 1. Если чётное, поделить на 2. В итоге вы получите новое число. Примените к нему те же правила, и продолжайте. Найдёте ли вы число, которое не приводит к 1? Можете попробовать самостоятельно.
Для начала Ааронсон, специалист по информатике, придумал альтернативную формулировку гипотезы Коллатца, т.н. «систему правил подстановки», с которой компьютерам было проще работать.
В системе правил подстановки вы работаете с набором символов, например, с буквами А, В и С. Вы используете их для формирования последовательностей: ACACBACB. Также у вас есть правила для преобразования этих последовательностей. Одно правило может говорить о том, что встречая АС, вы заменяете его на ВС. Другое может заменять ВС на ААА. Можно задать любое количество правил, определяющих любые преобразования.
Специалистам по информатике в основном нужно знать, всегда ли данная СП заканчивает работу. То есть, вне зависимости от того, с какой строки начинать, и в каком порядке применять правила, верно ли то, что строка в итоге превратится в состояние, в котором уже нельзя будет применить ни одного правила?
Ааронсон придумал СП с семью символами и 11 правилами, аналогичную гипотезе Коллатца. Если они смогут доказать, что его СП всегда заканчивает работу, они тем самым докажут, что гипотеза верна.
Чтобы превратить гипотезу Коллатца в задачу для SAT-решателя, Ааронсону и Хиюлу нужно было сделать ещё один шаг, связанный с матрицами, или массивами чисел. Им нужно было назначить уникальную матрицу каждому символу их СП. Такой подход – распространённый способ поисков доказательства того, что СП заканчивает работу – позволил бы им рассуждать о преобразованиях чисел через перемножение матриц. Семь матриц, обозначающих семь символов с СП должны были удовлетворять целому набору ограничений, отражающих соответствие 11 правил друг другу.
«Сначала вы пробуете подобрать матрицы, удовлетворяющие этим ограничениям, — сказал Эмре Йолчу, аспирант из университета Карнеги-Меллона, работающий над этой задачей с Хиюлом. – Если у вас получается, вы доказываете, что выполнение останавливается», и, следовательно, что гипотеза Коллатца верна.
На вопрос существования матриц, удовлетворяющих этим ограничениям как раз может ответить SAT-решатель. Ааронсон и Хиюл сначала запустили SAT-решатель на небольших матрицах 2х2. Рабочих вариантов они не нашли. Затем они попробовали матрицы 3х3. И снова безрезультатно. Они продолжали увеличивать размер матриц в надежде, что нужные найдутся.
Однако такой подход не может развиваться бесконечно, поскольку сложность поисков подходящих матриц растёт экспоненциально с ростом их размера. Хиюл предполагает, что современные компьютеры просто не справятся с матрицами размером более 12х12.
«Когда матрицы станут слишком сложными, вы не сможете решить задачу», — сказал он.
Хиюл всё ещё работает над оптимизацией поиска, пытаясь сделать его более эффективным, чтобы SAT-решатель мог проверять матрицы всё большего и большего размера. Они с коллегами работают над статьёй, подводящей итоги их текущим открытиям, но у них почти кончились идеи, и им, вероятно, вскоре придётся сдаться – по крайней мере, на какое-то время.
Ведь притягательность SAT-решателя состоит в том, что если бы у вас только получилось понять, как проверить ещё один случай, позвонить ещё одной няне, продлить поиски хоть ненадолго, вы, вероятно, могли бы найти искомое. В этом смысле главным преимуществом Хиюла может быть не его опыт работы с SAT-решателями, а его любовь к погоне за результатом.
«Я просто оптимист, — сказал он. – Я часто чувствую, что мне повезёт, поэтому я просто пытаюсь и смотрю, насколько далеко мне удаётся продвинуться».


