
Продолжение. Первая часть здесь.
Решение задачи
Отношение к полетам на Луну стало меняться в конце 1953 года, когда руководитель отдела прикладной математики Математического института АН СССР Мстислав Келдыш вызвал к себе аспиранта Всеволода Егорова и поручил ему просчитать траектории перелета на Луну. Причем как можно ближе к реальности. Когда Егоров спросил его о сроках, Келдыш ответил: «Побыстрее. Результаты нужны уже сегодня».
Отдел был создан изначально для расчета термоядерной боеголовки. Потом Келдыш получит «Героя соцтруда» за эту работу. Но как раз в 1953 году его выделили в отдельную организацию. Это позволило Келдышу более широко варьировать задачи, которые он мог ставить перед своими сотрудниками и аспирантами. Благо, кроме расчета термоядерных боеприпасов и ядерных реакторов, институт также решал вопросы по баллистическому обеспечению полета ракет, помогая ракетчикам решать на первый взгляд малозначительные, но для на самом деле важные задачи вроде оценки гарантийных запасов топлива.
Также хотел бы отметить, что коллектив тогда был как очень сильный, так и очень молодой. Сотрудников в воспоминаниях часто называли «мальчиками Келдыша». И не удивительно, он практически полностью сформировался в 1952-1955 годах из студентов близких курсов мехмата МГУ. В результате практически всем в этом коллективе было от 20 до 30 лет. Если выделить только коллектив, что занимался ракетно-космическими проблемами, то старше 30 лет было всего два человека: Собственно, Мстислав Келдыш и Дмитрий Охоцимский.
Коллектив был молодой. Космос будоражил кровь, а задачи, не решенные за столетия, казались легкими и понятными. Кроме всего прочего, как раз в 1953 году Егоров также организовал в институте постоянный семинар, посвященный космосу.
В результате, согласно статьям, Егоров в 1953-1955 годах успешно решил «плоскую» задачу полета на Луну, а в 1956-1957 — пространственную.
Конечно, вряд ли он бы справился за такое короткое время, если бы Келдыш не передал в его распоряжение так называемую специализированную цифровую машину – СЦМ. Собственно, уже сам этот факт весьма примечателен, так как начало 50-х – это заря цифровой техники. В частности, наша первая ЭВМ МЭСМ официально была запущенна в регулярную эксплуатацию только 25 декабря 1951 года. Но любые специалисты понимали, что подобную задачу без ЭВМ не решить.
Здесь было бы очень уместно поставить фотографию этой ЭВМ. Но, увы, я ее так и не нашел. Хорошо еще, что ее характеристики были указанны в статье посвященной облету Луны. Быстродействие ~ 100 операций в секунду, с оперативной памятью 64 ячейки, постоянная память на магнитных барабанах. Современный поиск по сайтам позволяет также сказать, что ее разработала СКБ-245, а в ее разработке принимал участие, в начале 1952 года, Малиновский.
Хотя, возможно, и в этих характеристиках кроется ответ, почему ее передали на расчет траекторий полета к Луне и почему сейчас ее так сложно найти.
Просто 100 операций в секунду — это и по тем временам слабый результат. Например, у БЭСМ-1 была скорость 8 000-10 000 операций в секунду, с оперативной памятью 2047 ячейки, а у Стрелы-1 – 2000 операций в секунду, оперативная память 2048 слов.
Серьезные ЭВМ стали решать серьезные задачи, а вот такие середнячки были переданы для решения разных дополнительных задач, а потом и вовсе забыты.
Но в любом случае, ЭВМ тогда были на острие технологий, требовались для решения многих проблем, и передача ЭВМ на такую задачу говорит о многом.
Серебряные лауреаты
Хронологически работа Егорова была, действительно, первой. Причем, что особенно важно, это было не просто теоретическое исследование. Именно благодаря этой работе проложили свой путь к нашему естественному спутнику «Луна-1», «Луна-2» и «Луна-3» в 1959 году.
Но, как часто бывает, близкие идеи приходят разным людям приблизительно в одно время. Так и здесь: в рамках 50-х годов задача о полете к Луне была решена еще несколькими людьми.
В СССР это был профессор Глеб Чеботарев. Тогда он работал (а в 1964 году стал его директором) в Институте теоретической астрономии АН СССР. Это был специализированный институт, созданный для изучения небесной механики. Точного текста его работы у меня, увы, нет; судя по упоминаниям в других материалах, он тогда рассмотрел несколько частных случаев. Но его работа все равно интересна, так как ЭВМ у него, скорее всего, не было. Впрочем, также возможно, что в его распоряжении были специализированные электромеханические дифференциальные анализаторы. Тогда они использовались для подобных целей.
Так как работа Егорова тогда была «закрытой», а Чеботарев, напротив, работал в совершенно открытом гражданском институте, то работа последнего в 1955-1957 стала куда более известной. О ней писали в научно-популярной литературе, а впоследствии утверждали, что именно она повлияла на траекторию «Луны-3» и многое другое.
Например, когда в США после запуска спутника бросились анализировать советские СМИ, там решили, что СССР ведет аж три разных проекта, связанных с полетом на Луну. Причем первый проект ведет профессор Чеботарев, а второй аспирант Егоров. Вот статья по этому поводу:
andreyplumer.livejournal.com/227077.html
Так ситуация обстояла в СССР, но и в США шли работы над полетами к Луне.
США
Первая ласточка точного математического исследования была в 1956 году. В начале этого года Роберт Бурхем из «RAND corporation» предложил использовать разрабатываемую тогда ракету «Тор-Айбл» для лунной миссии. 28 мая 1956 года был выпущен секретный отчет «Общий отчет о носителе лунных зондов». В нем рассматривались возможности запуска к Луне при помощи РН «Атлас». Занятно, но этого отчета на сайте «RANDcorporation» нет до сих пор. Зато есть два следующих, от июня 1956 года. Собственно, именно эта организация в 1956-1958 занималась лунными траекториями, пока после создания НАСА это не было поручено JPL. И именно они детально проработали идею лунных спутников, которые впоследствии превратились в первые зонды «Пионер».
Также нужно упомянуть Эрике Краффта (1917-1984). Он был одним из специалистов, работавших во время Второй Мировой в Пенемюнде. Как и многие другие немецкие специалисты, он потом попал в США. Краффт больше всего известен, как автор РБ «Центавр». Но он проводил и очень серьезные теоретические исследования. Его многотомник «Космический полет» в 60-х годах выпустили и у нас. Считается, что он не участвовал в программе «Аполлон» только потому, что в свое время разругался с фон Брауном. Так вот он тоже в период 1955-1957 г. явно получил доступ к ЭВМ и проанализировал многие особенности «лунных» траекторий. Также он один из тех немногих людей, кто был похоронен в космосе.
Так что же стало понятно при помощи ЭВМ?
Для начала, стал очевиден весьма неожиданный факт: никакого захвата Луной для объекта, запущенного с Земли, в сфере ее действия быть не может. По крайней мере, на первом витке. Скорости пролета внутри сферы Луны оказались больше местной параболической. Другими словами, аппарат, запущенный к Луне, может либо попасть в Луну, либо пролететь мимо нее с гиперболической (относительно Луны) скоростью, после чего либо вернуться к Земле, либо стать спутником Солнца.
Второй факт касался анализа возможных траекторий полета. Посмотрите на схему
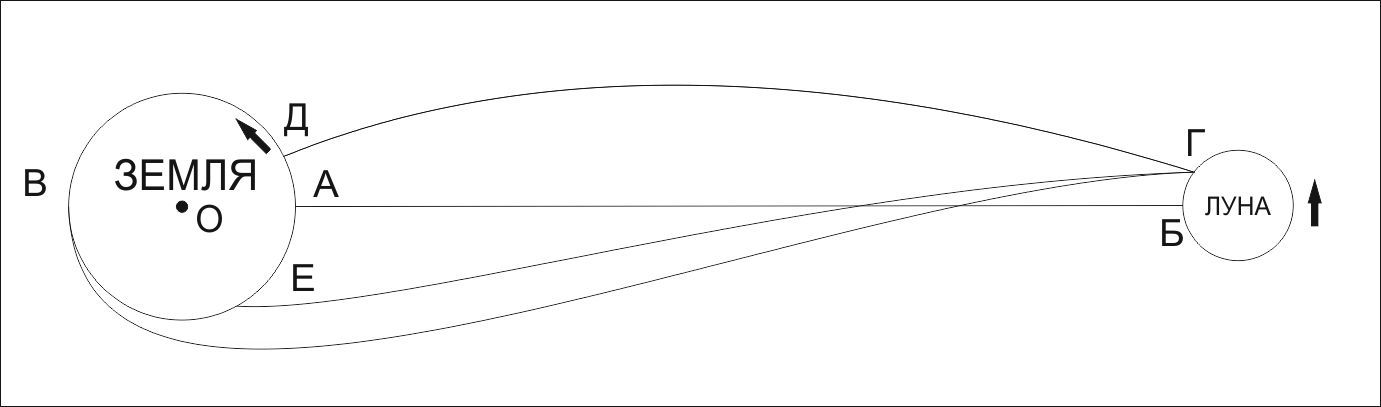
Это условный вид сверху на плоскость движения Луны. Стрелками обозначены вращение Земли вокруг своей оси (О) и орбитальное движение Луны. Теоретически все указанные траектории перелета возможны. В том числе и прямой перелет АБ, при достаточной скорости. Вот только он самый неоптимальный из всех. Самая энергетически выгодная траектория на схеме – это ВГ. Просто потому, что она максимально использует вращение Земли. Ведь угловая скорость вращения Земли не так и мала. На экваторе она составляет 460 м/с. В плоскости Луны несколько меньше. Но все равно, 300-400 м/с – совсем не лишняя добавка в начальную скорость, так как при полете к Луне даже десятки метров в секунду порой меняют картину полета. Для примера опять можно вспомнить «схему» Жюля Верна. По расчетам Гарсе, самая минимально возможная скорость полета к Луне, при достаточно серьезном допущении, составляет 11051 м/с. При этом вторая космическая скорость (то есть скорость, при которой снаряд улетит бесконечно далеко) при тех условиях составляла бы 11 188 м/с. Разность всего 137 м/с.
Если перевести сказанное выше на язык математики, то более оптимальная траектория – это та, у которой больше угол между точкой старта, центром Земли и направлением на Луну. То есть угол ВОА на схеме.
Выше рассмотрена так называемая плоская задача полета к Луне. То есть та задача, которая рассматривает перелеты в плоскости движения Луны. Так как она требует несколько более простых расчетов, то она была решена первой. Причем сразу после решения стало очевидно, что шансов на реальный полет внутри плоскости орбиты Луны достаточно мало. Просто потому, что для этого нужно, чтобы космодром находились на этой самой плоскости. При этом плоскость Луны меняет наклон к земному экватору с 18 градусов 18 минут до 28 градусов 36 минут с периодом 18,6 года.
Но любой космодром, расположенный на территории СССР, будет гарантировано вне плоскости орбиты Луны. Значит, придется лететь за пределами ее плоскости. Опять же, с точки зрения математики, для этого нужно, чтобы плоскость движения аппарата просто пересекала в нужной точке плоскость движения Луны.
Ниже, для примера, схема перелета станции «Луна-2»
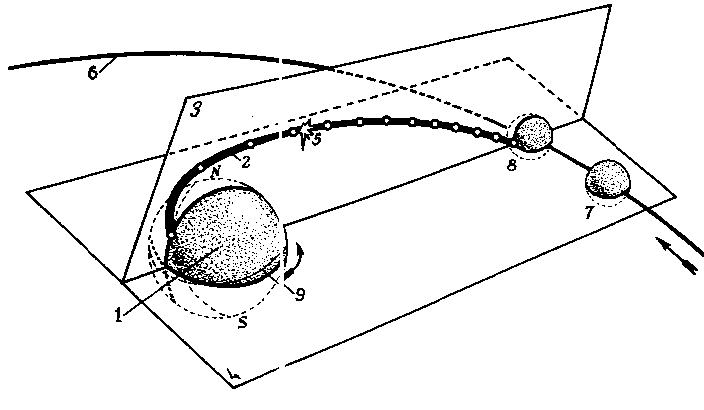
Как часто бывает, такая схема имела свои проблемы. В частности, она более требовательная к энергетике. Но, что хуже всего, при прямом перелете самый оптимальный фазовый угол просто не достижим.
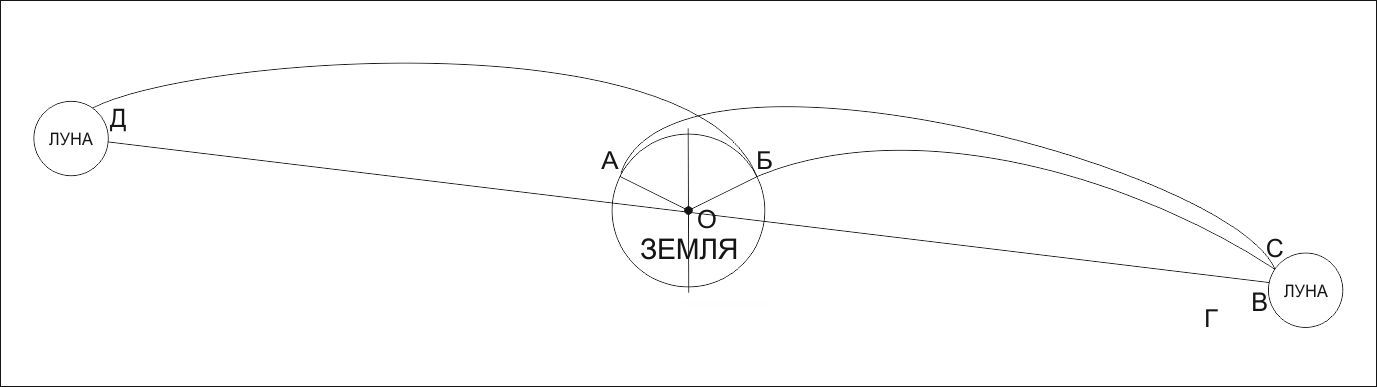
Вот схема. Для ее упрощения была выбрана полярная орбита корабля на пути к Луне, а сечение рисунка проходит через ось вращения Земли и плоскость орбиты Луны. Так вот предположим, что космодром располагается на широте АБ. Теоретически летать можно и по кривой БС, но благодаря вращению Земли всегда можно подгадать момент запуска под кривую АС. Вот только, увы, как можно видеть, даже в этом случае фазовый угол АОВ далек от оптимального. Более того, так как Луна с вращается вокруг Земли с периодом примерно 28 дней, в некоторые моменты ее расположение позволяет летать только по кривой БД. И энергетически кривые АС и БД очень сильно отличаются.
Например, согласно баллистическому отчету, подготовленному к полету «Луны-3», при запуске 4-6 октября 1959 года весовые потери в нагрузке относительно идеального случая были всего 6-26 кг. А вот при запуске 17-19 октября потери составили уже 418-444 кг. В случае «Луны-3» (запуск 4 октября 1959 года), суммарный вес всей полезной нагрузки составил 435 кг. Так что в определенные дни третья ступень «семерки» могла бы не вывести к Луне даже саму себя. Другими словами, оптимальная дата старта в этом методе – раз в месяц.
Еще более неприятный нюанс заключался в том, что, как уже сказано выше, угол между плоскостью вращения Луны и земным экватором постоянно меняется, с периодом в 18 лет. И при таком перелете самые оптимальные даты старта будут только раз в 18 лет.
Достаточно занятен тот факт, что как раз 1959 год был самым «плохим» для запуска с Байконура и благоприятным для запуска с мыса Канаверал. Но так как у нас тогда были достаточно мощные ракеты, этот факт остался практически незамеченным.
Также при расчете подобных орбит оказалось, что нужно учитывать еще и влияние Солнца, а не только Луны. Уже при первых расчетах стала очевидна важность наклона орбиты. А также то, почему орбиты всех планет находятся примерно в одной плоскости (плоскость эклиптики). Просто только данные орбиты стабильны. Например, Лидов провел такой расчет. Представим, что Луна находится на орбите с тем же размером большой полуоси, эксцентриситетом, периодом обращения и т. д., только под наклоном 90 градусов к плоскости движения Земли. И что тогда с ней будет? Оказалось, что она очень и очень скоро упадет на Землю. Всего через 55 месяцев. Этот результат тогда очень и очень удивил как астрономов, так и математиков. Но уже в 1959-1960 году «Луна-3» подтвердила правоту расчетов, упав на Землю под действием данного эффекта.
Именно по таким траекториям летали к Луне в 1958-1960 годах. Но достаточно быстро был предложен новый метод, который одновременно позволял максимизировать полезную нагрузку, причем при любой широте космодрома, и сильно уменьшить время ожидания стартового окна. Если при прямом «пушечном» перелете нужно было ждать 18 лет, а при прямом запуске с космодрома окно открывалось раз в месяц, то при новом методе можно было запускать ракеты хоть каждый день. Даже два раза в день.
Причем с точки зрения математики он очень прост. Нужно просто не пытаться сразу при старте с Земли выйти на траекторию полета к Луне. Можно сначала выйти на орбиту Земли, дождаться, когда фазовый угол станет оптимальным, после чего уже отправиться к Луне.

Вот схема. Точка А – момент запуска. АБ – выход на низкую орбиту спутника Земли. БВ – свободный полет по орбите. И в точке В переход на траекторию полета к Луне. Видно, что угол ВОС идеальный, а значит метод обеспечивает максимум полезной нагрузки. Собственно, сейчас именно так и летают практически все аппараты к Луне.
Этот метод у нас предложил Энеев. И он был детально разработан в конце 1959 года.
Несмотря на свою красоту с точки зрения математики, он требовал достаточно сложных технических решений. Нужно было разработать ракетный блок, который мог стартовать в невесомости, вакууме и после десятков минут свободного полета по орбите Земли. Причем все это время он должен был сохранять строго определенную ориентацию.
Чтобы аккуратно донести важность метода до ракетчиков, был даже разработан небольшой план. Вот как вспоминает ту историю Платонов:
Доклад по новой схеме полета должен был вести Охоцимский применительно к стартам к Венере и Марсу.
«Дмитрий Евгеньевич блестяще, и по-своему, решил проблему постепенного внедрения в сознание С.П. Королева и главных конструкторов понимания неотвратимости требуемых конструкторских разработок. К совещанию у Келдыша был подготовлен плакат с большим количеством (около 8-ми) просчитанных „плохих“ вариантов полетов к Венере и Марсу с негодными весами полезного груза этих вариантов и в конце — с двумя приемлемыми вариантами отмеченными звездочкой. Надо сказать, что плакат этот был выполнен в чисто академическом стиле — черной тушью на полу выпрямленном и так загибающимся листе ватмана, что эти „хорошие“ варианты, отмеченные звездочкой, были сидящим в мягких креслах „главным“ даже не очень видны.
Дмитрий Евгеньевич не был бы самим собой, если бы он сразу перешел к двум последним вариантам. Вместо этого он стал по очереди, один за другим, подробно описывать сверху вниз все просчитанные краевые задачи и объяснять все баллистические недостатки непрерывного способа разгона КА. В принципе присутствующим все стало понятным уже после разбора второго из вариантов, и где-то в середине рассказа о третьем, уж очень не подходящем варианте полета, Сергей Павлович спросил: „Дмитрий Евгеньевич! А что у Вас там внизу, со звездочкой?“ на что получил очень вежливый ответ: „Сергей Павлович, я об этом скажу обязательно чуть позже“, и рассказ обстоятельств очередного варианта продолжился. Спустя еще один или два варианта ситуация повторилась, повторилась она и в третий раз. На этот раз Сергей Павлович уже не просил, а очень раздражено (он просто взорвался) потребовал: „Дмитрий Евгеньевич! Да скажите, наконец, что у Вас там внизу, со звездочкой“?». Атмосфера весьма накалилась, и в наступившей тишине раздался тихий и спокойный голос Мстислава Всеволодовича: «Дмитрий Евгеньевич! Ну, выполните же, пожалуйста, просьбу Сергея Павловича!» Последовал подробный рассказ о «звездочке». И тогда после некоторого молчания произошло подробное обсуждение, и было принято чисто эпохальное решение -звездочку делать!»
И снова нужно уточнить один момент. До сих пор время от времени возникают идеи о сборке лунных миссий на орбите Земли (например, на МКС). Во многом это – наследие идей 50-х годов (Вернера фон Брауна и прочих), которые оценивали такой полет, еще толком не зная особенности лунных траекторий. Либо, как вариант, говорят о запуске лунных станций на орбиту Земли попутным грузом, с последующим запуском к Луне. Как можно видеть, запуск на первом витке к Луне возможен только при очень аккуратном фазировании плоскости орбиты спутника Земли с траекторией перелета к Луне. Практически нет шансов, что орбита, предназначенная для другого аппарата, позволит сделать это. Значит, нужно ожидать на орбите нужного момента времени. С учетом траектории Луны, подобное окно открывается только два раза в месяц. А с учетом требований по освещенности Луны – даже раз в месяц. Более того, подобное окно может оказаться тоже не оптимальным, так как вполне может случиться, что в момент совпадения плоскостей станция окажется не в требуемой точке В, а в Б или вообще с другой стороны Земли. А это очень сильно изменит фазовый угол и увеличит энергетику.
В результате, требуемый момент старта можно будет ожидать в течении нескольких месяцев. И необходимо, чтобы аппарат был рассчитан на подобные режимы работы. При том, что до Луны, по сути, лететь всего несколько дней.
Другими словами, запуск к Луне с произвольной орбиты спутника Земли совсем не лучшее решение. Конечно, если на орбите Земли ждет буксир с ЯРД или ЭРД, который может компенсировать многие ошибки при выведении, этот вариант допустим. 🙂 Но во всех других случаях лучше стартовать с Земли.
Что-то вроде послесловия
Я уверен, что очерк выше достаточно точно описывает подход, который был в то время к полетам на Луну. Для этого пришлось проанализировать много документов на разных языках, и общая картина была именно такой. До 50-х годов большая часть авторов оценивала полет именно по схеме Жюля Верна. А после 50-х годов все уже начали ссылаться на расчеты вышеприведенных авторов. Но все-таки. Ведь постановка задачи была известна и до 50-х. Были известны численные методы решения дифференциальных уравнений, существовали самые разные приборы для ускорения вычислений. От арифмометров до специализированных дифференциальных вычислителей. Значит, теоретически мог быть и человек, который решил положить годы своей жизни на подобные вычисления. И узнал правду о подобных полетах задолго до появления ЭВМ. Вот только был ли он в реальности?
Очень может быть. История, как обычно, куда сложнее чем сначала представляется.
Читая статью Фридриха Цандера «Теория межпланетных путешествий» 1922-1925 года из вот этого сборника, я заметил достаточно занятную сноску под словами «Аппарат, предоставленный самому себе, опишет сложную кривую», посвященными траектории облета Луны.
«Эти кривые отчасти исследованы Стрёмгреном в Копенгагене механической квадратурой. Его исследования длятся уже 12 лет».
Так как нет слов «Прим. редактора» — это явно примечание Цандера от тех лет.
Речь про шведско-датского астронома Сванте Стрёмгрена (1870-1947). Он был профессором астрономии в Копенгагенском университете и директором Копенгагенской обсерватории.
Увы, каких-либо подобных его трудов я так и не нашел. Только скромные упоминания в других работах. Возможно, если он и сделал подобную работу, то не опубликовал. Может, издать ее помешала война, а потом смерть. Ну, или опубликовал в совершенно неизвестном журнале. В любом случае, следует признать, что если работа и была, то никак не повлияла на представления тех лет о полетах на Луну.
Собственно этот материал написан на базе моей книге посвященной Луне. И я очень благодарен
lozga и Zelenyikot за поддержку. Если понравилось, постараюсь опубликовать на этом ресурсе посты по поводу посадки на Луну и по разным частным вопросам.
Источник


