С Земли на Луну. История и математика. Часть 1

Если уходить в историю изучения траекторий полета с Земли на Луну, то необходимо вернуться на полтора века назад, в 1865 год, когда был опубликован новый роман Жюля Верна «С Земли на Луну прямым путём за 97 часов 20 минут». Конечно, это была далеко не первая книга, в которой описывался подобный перелет, но это был первый роман, в котором автор решил подойти к описанию путешествия с научных позиций.

Причем уровень подготовки данного текста особенно хорошо понятен сейчас, так как впервые не просто было показано космическое путешествие, но и детально проанализированы все нюансы, порой весьма мелкие. Сейчас роман любят критиковать за те ошибки, что допустил автор. Но при таком объеме работы было бы удивительно, если бы там вообще не было ошибок! И сейчас куда больше поражают не его ошибки, а то, в чем он оказался прав. Например, по своей идее системы очистки кислорода как на снаряде Колумбиады, так и на космическом корабле «Союз» очень похожи. Только у Жюля Верна был гидроксид натрия, а сейчас применяют гидроксид лития.

Еще более интересны те моменты, в которых он оказался прав, несмотря на неверные предпосылки. Например, Перельман его критиковал за то, что он привел ошибочные данные по времени перелета с Земли на Луну и даже вынес их в название романа. Математик провел более точные расчеты по указанному методу, получив цифру порядка шести суток, на двое суток больше, чем в романе. И его расчеты, в рамках этого метода, действительно были правильными. Только за четверо суток долететь до Луны действительно можно (собственно, многие аппараты достигали Луны примерно за это время), а вот за шесть суток уже нельзя.Метод расчетов был выбран фантастом неправильно, а цифра получилась верная!

Еще, например, вскоре после выхода романа «Вокруг Луны» многие сомневались в возможности подобной траектории близкого облета Луны под действием только гравитационных сил. Лишь в начале ХХ века, при оценке орбит в системах двойных звезд, действительно была показана возможность существования подобных орбит. Вот что писал английский журнал «Знание» в начале ХХ века в статье «Астрономия у Жюля Верна»:

«Кривая, описанная снарядом Ж. Верна, дает повод к весьма интересным вопросам. Она начинается и кончается на Земле и представляет собою замкнутую орбиту снаряда. Такую орбиту должна описывать частица, выброшенная с Земли и подверженная действию только силы земного тяготения. Но под одновременным действием Земли и Луны форма орбиты, очевидно, должна измениться. Это было указано впервые, кажется, Бюрро, исследовавшим различные относящиеся сюда частные случаи. Джордж Дарвин также исследовал подобные случаи. Но лишь недавно была дана общая теория этого вопроса профессором Ф. Р. Мультоном, который доказал существование подобных орбит и нашел необходимые начальные условия их существования. Жюль Верн надолго предвосхитил все эти исследования, и надо, конечно, поставить ему в заслугу убедительную разработку этого вопроса».

Другими словами, задачи, которые попытался решить тогда Жюль Верн, были не просто на переднем крае науки – они часто ставили вопросы, на которые наука тогда не могла дать ответа.

Впрочем, не нужно забывать, что все это он делал не один. При написании всех своих книг автор старался обратиться к специалистам в какой-либо области. Согласно его дневникам, расчеты для перелета с Земли на Луну провел его кузен Анри Гарсе (1815-1871), преподаватель математики в лицее Наполеона (сейчас лицей Генриха IV). Кстати, здесь можете посмотреть его книгу на французском языке, посвященную Космографии Leçons nouvelles de Cosmographie (1854). И его расчеты были достаточно точны. Например, здесь я по данным, приведенным в книге, вычислял точную дату старта экипажа Колумбиады.

Henri Garcet (1815–1871)

Впрочем, мы бы, возможно, так и не узнали про его расчеты, если бы Жюль Верн не поместил их в самое начало книги «Вокруг Луны», использовав их в беседе экипажа снаряда Колумбиады. Пишут, что читатели газеты «Дебаты» от 7 ноября 1869 года были буквально поражены, увидев сложные математические вычисления — в этой газете началась публикация романа.

Вот как была описана математическая модель перелета устами Мишеля Ардана и Барбикена:

— А знаешь, Барбикен, о чем я думал всю ночь?
— О чем? — спросил председатель.
— Я все думал о наших кембриджских друзьях. Ты, конечно, заметил, что я ни черта не смыслю в математике. Так вот: я никак не могу понять, каким образом наши ученые в обсерватории могли вычислить скорость, которую должен иметь снаряд, чтобы долететь до Луны.
— Ты хочешь сказать, — перебил Барбикен, — до той нейтральной точки, где силы земного и лунного притяжения одинаковы, потому что с этой точки, которая находится почти на девяти десятых всего расстояния между обеими планетами, снаряд полетит на Луну сам собой, вследствие собственной тяжести.
— Ну да, именно это я и имел в виду, — сказал Мишель.- Но как же все-таки они вычислили эту скорость?
— Ничего нет легче.
— А ты сумел бы сам провести это вычисление?
…
— Да, дорогой друг. Приняв в расчет все известные условия задачи:
расстояние от центра Земли до центра Луны, радиус Земли, массу Земли, массу Луны, я могу с точностью установить начальную скорость нашего снаряда, и при этом с помощью самой простой формулы.
— Какая же это формула?
— А вот увидишь. Но только я не стану вычеркивать кривой, описанной нашим снарядом между Луной и Землей, учитывая их относительное движение вокруг Солнца. Предположим, что обе планеты неподвижны. Этого будет совершенно достаточно.
— Почему же?
— Потому что именно так решаются задачи, называемые «задачами трех тел», интегральный же метод для решения таких задач еще недостаточно разработан.

Через некоторое время была выведена и формула, которая была представлена читателям:

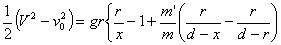
где r-радиус Земли, -расстояние между центрами Земли и Луны, х- расстояние ядра от Земли.V₀ — начальная скорость ядра. V- скорость на расстоянии х.

А перелет выглядел так

Здесь я хотел отметить, что эта формула при указанных начальных данных действительно верна. И действительно точно отображает гравитационное воздействие Земли и Луны на аппарат в любой момент времени. Её достаточно легко вывести исходя из закона сохранения энергии.

Так в чем же дело? Проблема в том, что она не учитывает динамики системы. Луна же вращается вокруг Земли со скоростью около 1 км/с. Именно в этом заключается проблема данной задачи. В результате, при попытке перелета по указанной выше схеме, когда станция подлетит к нейтральной точке между Землей и Луной, она вовсе не будет захвачена полем Луны, так как последняя улетит от снаряда со скоростью километр в секунду, и снаряд начнет падать на Землю. Но тогда была надежда, что захват аппарата Луной все-таки произойдет, и подобная схема в первом приближении точно показывает динамику перелета. С легкой руки Жюля Верна подобный метод расчета полета вскоре стал очень популярным. Его стали использовать не только в художественных книжках, но и в серьезных научных работах.

Нужно отметить, что тогда астрономы как раз понимали важность учета динамики. Да и дифференциальные уравнения, учитывающие как гравитацию, так и динамику, тогда могли легко составить. Вот только также никак не удавалось найти простое их решение. Собственно, как сейчас хорошо понятно, задача трех тел не имеет общего аналитического решения.Задачу можно было решить только численно, что означало очень и очень большое количество рутинных вычислений, на которые можно было потратить месяцы или даже годы жизни. На момент опубликования романа подобную задачу решали численным методом всего два раза. Причем первая попытка была более чем за сто лет до публикации романа, в 1759 году.

Известно, что Эдмунд Галлей, составляя каталог комет, заметил, что у нескольких комет, появившихся на небе в разное время, очень похожие параметры. Сверив их, он решил, что это может быть одна и та же комета. Потом ее назовут его именем. Комета Галлея появлялась на небосводе в 1531, 1607 и 1682 годах. То есть период обращения был 75-76 лет, а следующее появление ученый спрогнозировал на 1758 год. И все было бы замечательно, если бы не одно «но»: в расчетное время комета на небе так и не объявилась.

Тогда французский математик Клео решил рассчитать ее траекторию как можно точнее. В том числе, с учетом возмущений ее траектории за счет притяжений Юпитера и Сатурна. Это был очень утомительный и долгий труд, хотя он делал эту работу не один: ему помогали астроном Ж.Лаланд и математик мадам Лепот. Оказалось, что разница с предыдущими оценками периода обращения кометы составляет 618 дней, и она прибудет к своему перигелию 13 апреля 1759 года. С возможной ошибкой на месяц. Оценка оказалась очень точна: комета прошла свой перигелий 12 марта. Это была как победа математиков, так и очень хорошее подтверждение законов Ньютона.

Про этот расчет Лаланд после писал: «Шесть месяцев мы вычисляли с утра и до ночи, иногда даже не отрываясь от еды, и следствием этого было то, что я расстроил свое здоровье на все остальные дни своей жизни. Помощь госпожи Лепот была такова, что без нее мы никогда не осмелились бы предпринять этот громадный труд, состоявший из вычислений расстояния кометы от двух планет — Юпитера и Сатурна — для каждого градуса небесной сферы в течении 150 лет».

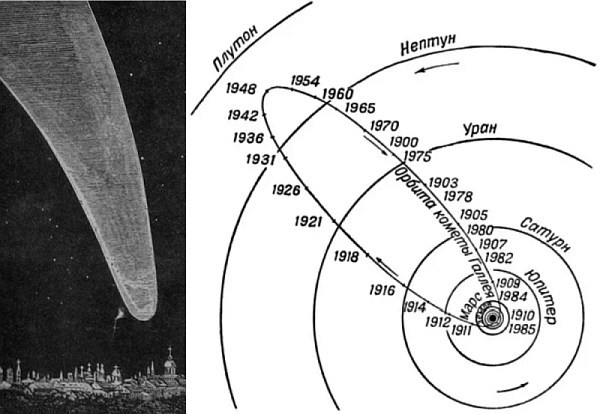
Можно посмотреть траекторию кометы Галлея относительно орбит планет

Второй раз подобный метод был применен в 1829 году, опять при расчете траектории кометы Галлея. Оценки дали дату возвращения кометы к Солнцу –15 ноября 1835 года. Комета вернулась 16 ноября, опоздав всего на сутки.

В результате, подобный численный метод доказал свою точность. Но по приведенной выше истории хорошо видно, насколько большая и утомительная работа при этом требовалась. Полгода работы трех математиков ушло на вычисление всего одной траектории с хорошо известными начальными параметрами! А ведь для вычисления траекторий перелета с Земли на Луну нужно было оценить десятки, если не сотни траекторий, с разными начальными параметрами. Иначе никак нельзя получить, скажем, точную скорость, дату старта, характеристики траектории, возможные погрешности, параметры полета станции рядом с Луной и т. д. На это уже могли уйти годы жизни. То есть данный вариант решения считался очень сложным. Особенно для задачи, не имеющей тогда особого практического смысла.

При этом, также тогда была уверенность, что можно найти аналитическое решение задачи трех тел. Хотя бы позволяющее, в первом приближении, оценить параметры перелета.

И метод, предложенный Жюлем Верном, казалось, давал ответ на этот вопрос. Ведь математически, в рамках начальных допущений, он был безупречен. Да, он не учитывал динамику, но тогда многие ожидали, что такое допущение нормально, и реальная траектория движения снаряда с Земли на Луну будет выглядеть как-то так.

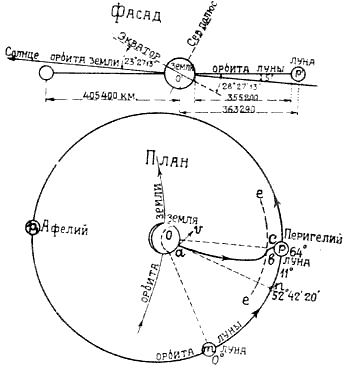
Расчет из книги «Космические корабли. (Межпланетные сообщения в фантазиях романистов)» 1928 год

И математическая красота вкупе с большой популярностью романа сыграла злую шутку: по данному методу оценивали перелет практически все пионеры космонавтики – Годдард, Штернфельд, Оберт, Макс Валье и многие другие. Иногда, крайне редко, также оценивали не прямой перелет, а по эллипсу спутника Земли. Но и в этом методе были свои недочеты. Например, и там многие почему-то были уверены, что для достижения Луны достаточно попасть в сферу ее действия; дальше, мол, притяжение Луны должно сделать все остальное. Хотя, как было сказано выше, возможность облета в задаче трех тел уже была доказана.

Хорошей иллюстрацией будет статья Вернера фон Брауна в еженедельнике от 18 октября 1952 года.В ней фон Браун рассказал, как, по его мнению, будет выглядеть экспедиция на Луну.

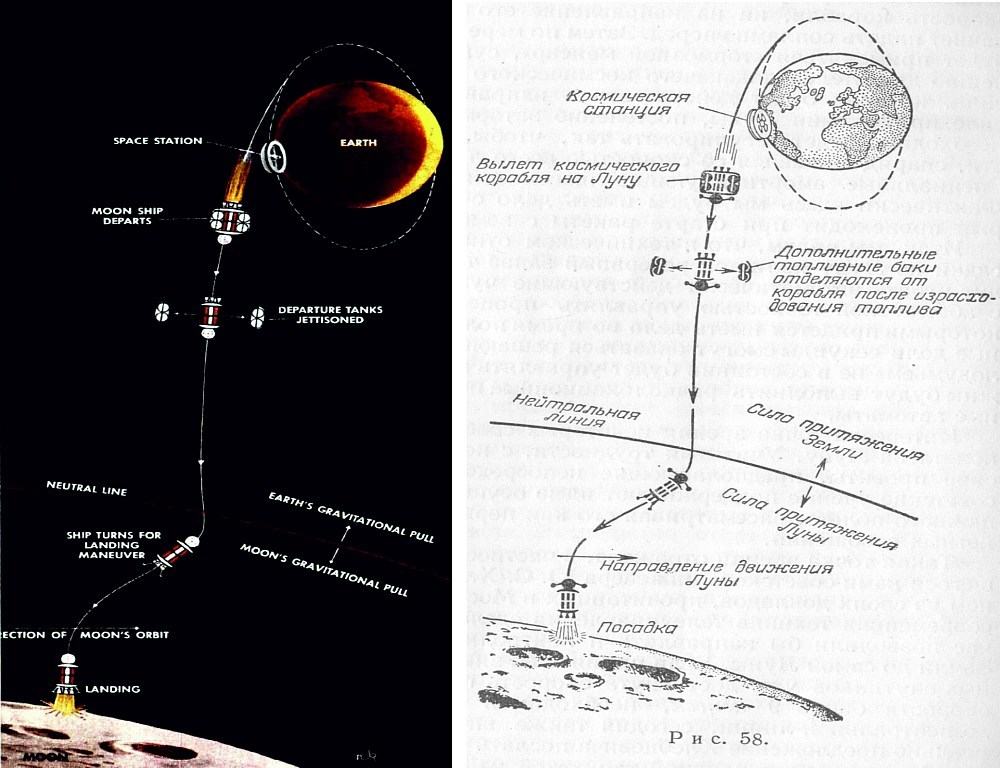
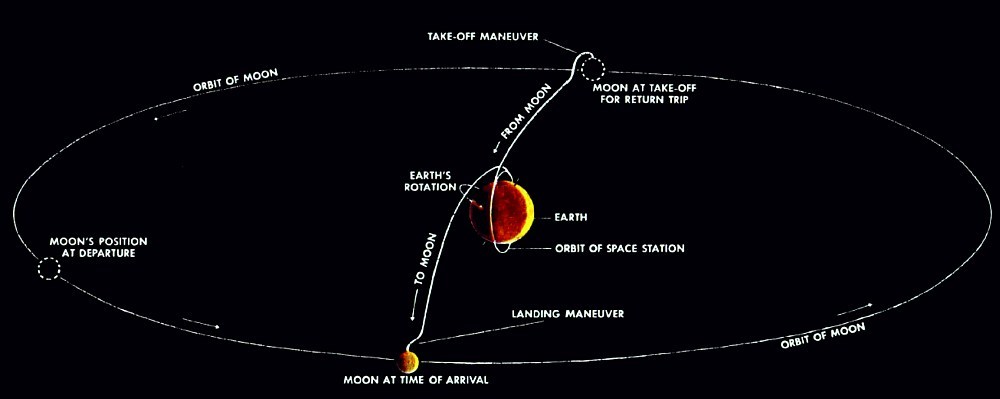
Саму статью можно скачать здесь

По иллюстрации хорошо видно, что там представлена именно схема Жюля Верна: сначала достижение нейтрального района между Землей и Луной, впоследствии – падение на Луну под действием ее притяжения. Пушка давно заменена на ракету, но основной принцип остался неизменным. Хотя прошла почти сотня лет после опубликования романа.

Но вскоре подход к перелетам с Земли на Луну стал меняться. В том числе, благодаря развитию электронно-вычислительных машин.

Продолжение следует.