Недавно радужные раскраски помогли провести новое доказательство. И они уже не в первый раз оказываются полезными.
Цветовое кодирование латинского квадрата и его графа может многое о них рассказать
Недавно мы рассказывали о новом доказательстве гипотезы Рингеля. Часть доказательства была связана с использованием радужных раскрасок, особого способа цветового кодирования для визуализации информации. Однако подобные раскраски довольно давно используются математиками для облегчения решения загадок, и сейчас эту технику пытаются применить к задаче, связанной с предыдущей.
Гипотеза Рингеля – это задача из области комбинаторики, связанная с построением графов – точек (вершин), соединённых линиями (рёбрами). Она предсказывает наличие особого взаимоотношения между крупными графами определённого типа с 2n + 1 вершиной и пропорционально меньшими графами с n + 1 вершиной.
Начнём, к примеру, с 11 вершин. Соединим каждую вершину со всеми остальными, чтобы получить т.н. полный граф. Далее, возьмём шесть вершин из имеющихся, и соединим их, как нам заблагорассудится, только чтобы у нас не получилось замкнутых петель. Таким образом мы получим т.н. «дерево».

Примеры полных графов и деревьев
Гипотеза Рингеля говорит, что копиями любого дерева можно идеально покрыть, или замостить, все рёбра соответствующего полного графа – так, как одинаковыми плитками можно замостить пол кухни.

Как и с кухонным полом, для успеха необходимо подобрать правильное расположение первой плитки. Три математика, придумавшие доказательство, закодировали цветом ребра полного графа на основе расстояния между вершинами, чтобы найти это расположение.
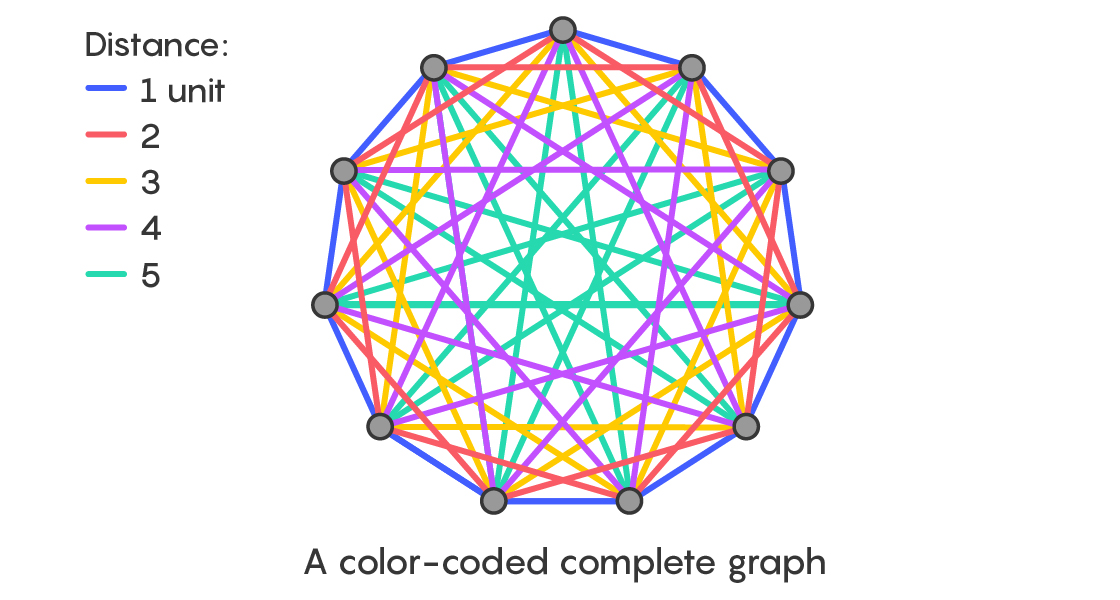
Затем они попытались расположить дерево внутри полного графа так, что оно покрывало по одному ребру каждого цвета. Показав, что такое «радужное» расположение возможно в любом случае, они доказали, что идеальное замощение, предсказанное Рингелем, работает всегда.
Однако такая техника радужной раскраски не первый раз пришла на помощь.
В XVIII веке Леонард Эйлер заинтересовался чем-то вроде судоку для детей. Возьмём квадрат 3х3 клеточки. Эйлер заполнил его так, чтобы в каждой строке и каждом столбце находились числа от 1 до 3, ни разу не повторяясь. Подобная головоломка называется латинским квадратом. У закономерностей и техник, открытых Эйлером и другими математиками при изучении латинских квадратов, есть связь со многими различными областями математики.
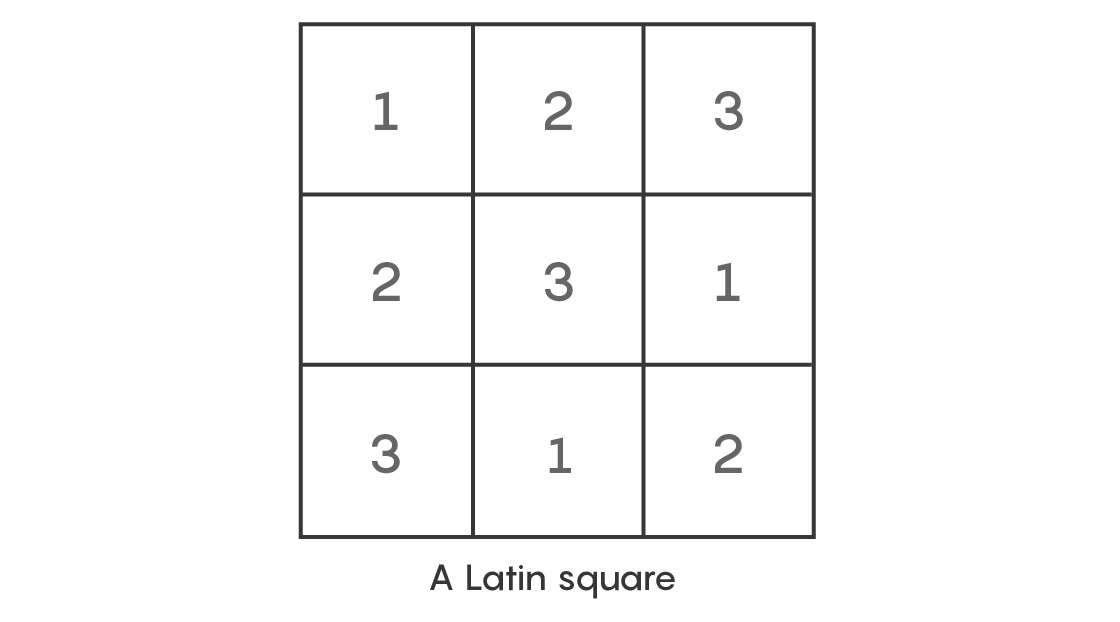
Затем Эйлер задался вопросом: можно ли выбрать три клеточки, по одной из каждого столбца и каждой строки, так, чтобы числа в них не повторялись? Допустим, можно выбрать клетку из первого столбца первой строки, содержащую 1, клетку из второй строки второго столбца, содержащую 3, и из третьей строки третьего столбца, содержащей 2. Итак, мы выбрали три клетки, каждая из которых принадлежит разным строкам и столбцам, и содержит своё число – 1, 3, 2. Такой набор клеток называется трансверсальным.
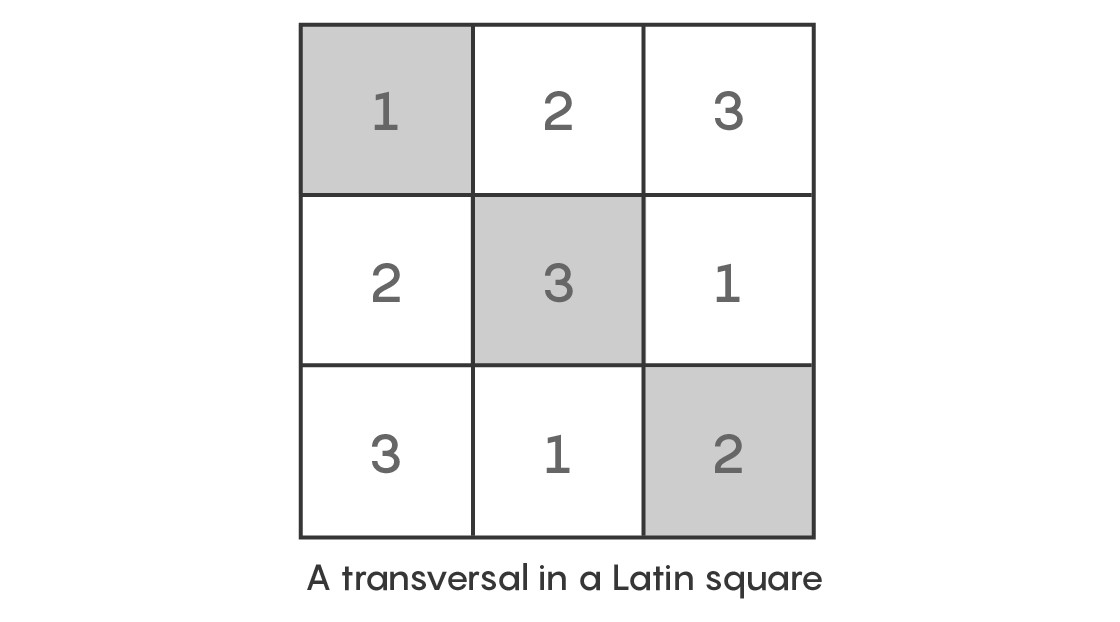
Эйлер хотел знать, можно ли поделить всю сетку 3х3 (или квадратную сетку любого размера) целиком на трансверсальные множества, так, чтобы в каждом множестве было по одному числу с каждой строки и каждого столбца. То есть, в случае квадрата 3х3 хотелось бы надеяться на то, что мы сможем найти три различных трансверсальных множества, покрывающие вместе все клетки квадрата.
В итоге математики обнаружили, что один из способов исследовать этот вопрос – превратить квадрат в граф. Для этого нарисуем слева три вершины, обозначающие три столбца. Потом нарисуем справа три вершины, обозначающие строки. Нарисуем рёбра, соединяющие каждую вершину справа с каждой вершиной слева. Каждое ребро, будучи комбинацией определённой строки и столбца, представляет одну из девяти клеточек. К примеру, ребро между верхней правой вершиной и верхней левой вершиной соответствует клетке первой строки первого столбца (верхняя левая клетка латинского квадрата).

Теперь достанем цветные карандаши и закодируем цветами рёбра в соответствии с тем, какие числа квадрата они обозначают. Допустим, синим мы раскрасим линии, обозначающие 1, красным – 2, жёлтым – 3. Если в левой верхней клетке стоит 1, тогда ребро между верхними вершинами будет синим.

Посмотрим на цвета рёбер. Можно ли выбрать три ребра каждого из трёх цветов так, чтобы они начинались и заканчивались в разных вершинах? Такой набор называется радужным соответствием. Если найти его, станет понятно, что в соответствующем латинском квадрате имеется трансверсаль. Более того, если найти три разных радужных соответствия, станет ясно, что весь латинский квадрат состоит из трансверсалей.

Радужные раскраски помогали исследователям изучать задачи в прошлом, а также стали ключевым элементом нового доказательства гипотезы Рингеля. Они также играют роль в ещё более сложной задаче, гипотезе грациозной разметки.
Чтобы понять, в чём суть задачи, для начала начертите шесть вершин, а потом соедините их так, чтобы получилось дерево. Назначьте каждой вершине номер любым способом. Затем разметьте каждое ребро разницей между номерами вершин, которые оно соединяет. То есть, к примеру, если ребро соединяет вершины 6 и 2, то мы помечаем это ребро числом 4.
Ваша цель – сделать так, чтобы метки рёбер шли последовательно, и их номера не повторялись. В данном случае – 1, 2, 3, 4, 5. Если вы сможете так сделать, тогда для вашего дерева будет существовать грациозная разметка.

В 1960-х Герхард Рингель – тот самый, что выдвинул гипотезу – и Антон Коциг, вместе предположили, что любое дерево, вне зависимости от количества рёбер или формы, можно разметить грациозно.
Гипотеза грациозной разметки подразумевает гипотезу Рингеля – то есть, если верна первая гипотеза, то верна и гипотеза Рингеля. Чтобы понять это, вернёмся к грациозно размеченному дереву из шести вершин и полному графу из 11 вершин. Распределим эти 11 вершин по окружности и пронумеруем их от 1 до 11. Теперь разместим копию дерева на полном графе так, чтобы метки вершин совпадали: вершина 5 дерева наложится на вершину 5 полного графа, и так далее. Такое размещение оказывается радужной копией грациозно размеченного дерева.
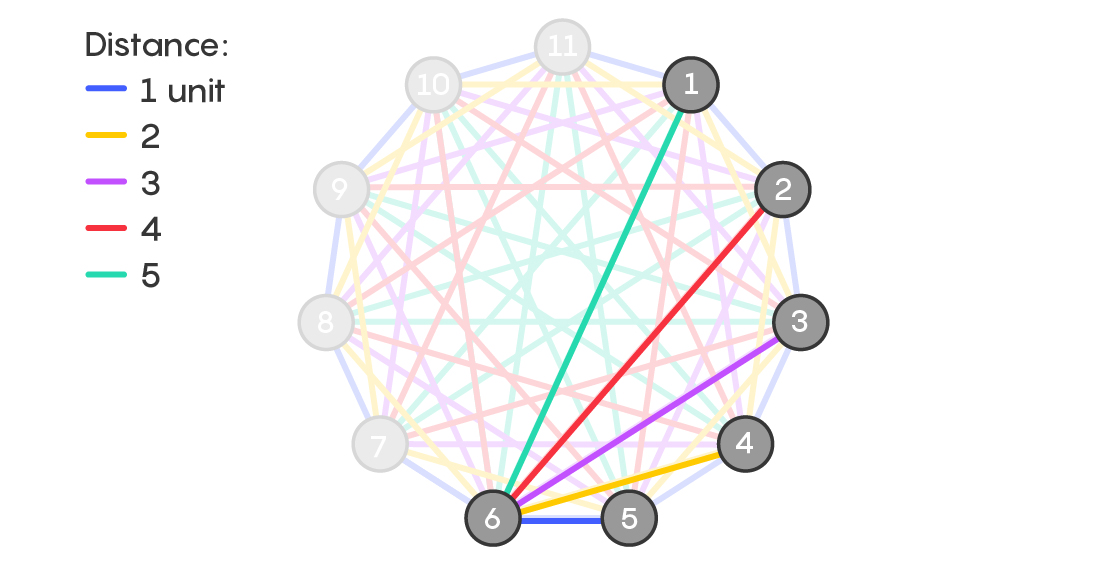
Так что если вы знаете, что деревья с количеством вершин n + 1 всегда можно грациозно разметить, тогда вы знаете, что их всегда можно разместить внутри соответствующего полного графа с 2n + 1 вершин так, чтобы получить радужную копию дерева. И такое размещение как раз будет ровно той позицией, с которой нужно начинать процесс замощения Рингеля.
«Если вы найдёте грациозную разметку, я смогу рассказать вам, как найти вашу радужную копию», — сказал Бенни Судаков из Швейцарского федерального технологического института, один из трёх авторов доказательства гипотезы Рингеля.
Конечно, математики в итоге смогли доказать истинность гипотезы Рингеля без необходимости доказывать гипотезу о грациозной разметке, оставив этот вопрос без ответа.
«Грациозная разметка – вопрос сам по себе привлекательный и красивый, и до сих пор остаётся открытым», — сказал Судаков.
Однако методы, позволившие прийти к доказательству гипотезы Рингеля, вероятно, можно применить и к грациозной разметке – и математики с нетерпением хотят узнать, насколько далеко эти методы могут их завести.

