Самые распространённые элементы во Вселенной — это водород (около 73%) и гелий (около 25%), поэтому двух- и трёхатомные молекулы, которые формируются из них — это в количественном отношении самые главные молекулы для всей вселенской астрохимии. В этом посте мы взглянем на них с точки зрения квантовой химии. Все, кому не безразличны электроны и их жизнь, как говорится, велком под кат 🙂
Введение
Космос велик. Страшно велик. Вы просто не поверите, насколько умопомрачительно он велик. К примеру, вы сетуете, как далеко от вас аптека — но по сравнению с космосом это сущая чепуха. [1] И в космосе у нас не так уж много настоящего вещества, того, из которого мы сами и состоим: положительно заряженных ядер и отрицательно заряженных электронов. В общем, наша (барионная) материя, по современным оценкам в рамках модели ΛCDM, составляет около 5% всего что есть во Вселенной, а всё остальное — это чёрная магия Тёмные Энергия и Материя. [2]

Из этих 5% всего, что мы можем видеть во Вселенной (во всяком случае прямым образом), больше всего и по массе и по количеству, составляют атомы водорода и гелия. Например, в нашем Солнце, вокруг которого вращается наш Голубой Шарик, около 73% водорода, и около 25% гелия, а всё остальное — это, как говорят астрономы, всякие металлы. [3] И такой состав более-менее отражает состав всей Вселенной.
И естественно, при таком составе нашей Вселенной, глупо думать, что всякие органические молекулы составляют достаточно заметный процент от всего сущего. Ведь если мы возьмём наугад один атом в произвольном месте Вселенной, он с вероятностью около 3/4 окажется атомом водорода, с вероятностью около 1/4 — атомом гелия, и с гораздо меньшей вероятностью — ещё чем-то другим (углеродом, азотом, кислородом, железом, и т.д.). А для образования молекул, нам нужно чтобы встретились два атома, поэтому больше всего молекул (в первом приближении) будет образовываться таких, которые состоят только из ядер водорода, потом, из водорода и гелия, и потом из гелия и гелия. Количество электронов при этом может меняться, т.к. атомы во Вселенной не обязательно имеют достаточное количество электронов, чтобы называться этими самыми атомами. Так что самыми главными молекулами во Вселенной, по версии этого текста, я нареку катион1 H2+, молекулу водорода H2, анион2 H2—, катион HHe+, и нейтральные комплексы (почему это не молекулы, мы поговорим дальше) HHe и He2. На самом деле, мы выкидываем ещё важные штуки, типа катиона H3+, но он чуть более сложный, и заслуживает отдельного разговора.
На самом деле заголовок и космическое вступление — это уловка, (мискузи). В этой статье мы будем говорить в первую очередь о том, как они устроены, и почему они так устроены. Ну и немного поговорим о том, как эти молекулы формируются в космосе, и как их в космосе находят.
Истинная причина написания этого текста
Причина проста: я делал лекцию о методе молекулярных орбиталей, и мне понадобились данные о корреляции порядка связи с различными данными. Такой информации полно во всяких книгах по общей химии, но выбор молекул для иллюстрации какой-то рандомный, а данные непонятно откуда получены. Поэтому, в соответствии с лозунгом: хочешь что-то хорошее найти, делай это сам, я взял любимый квантово-химический пакет, рабочий кластер, и за час посчитал всё, что мне было нужно. И этим я и хотел поделиться, авось кому ещё нужно.
2 orbitals 1 (or few) electron
Молекула, или ион — это просто сборище ядер и электронов, которые удерживаются вместе, и никуда не разбегаются. Атомы водорода и гелия — это элементы первого периода, и как мы помним из школьной химии, это означает, что у них активна для образования связей только одна орбиталь, 1s, на которой могут сидеть два электрона, один со спином вверх (↑), другой со спином вниз (↓). И для того, чтобы образовать стабильную электронную конфигурацию, этим атомам нужно где-то заполучить эти самые два электрона на свою 1s, а иначе у нас вместо довольного и счастливого атома будет похотливый и ненасытныйщенный радикал, который будет искать где-бы добыть ещё один электрон.
Если у нас нейтральный атом водорода, то в его ядре находится всего один протон, поэтому заряд у него (в единицах модуля заряда электрона) составляет Z=+1, поэтому у нейтрального атома водорода есть всего один электрон на 1s орбитали, и он несчастлив сам по себе, ему нужен где-то ещё один электрон, и именно поэтому основная форма существования водорода — это двухатомная молекула H2, в котором электроны делятся своими электронами, образуя ковалентную связь. А у гелия же всё замечательно. Его порядковый номер в Таблице Менделеева — это два, в честь двух протонов в его ядре, поэтому нейтральный гелий имеет заполненную первую электронную оболочку, что делает его счастливым и химически нейтральным атомом инертного газа, которому никто не нужен.
Как же формируется ковалентная связь? Об этом я писал подробно в двух (уже весьма старых) постах на Хабре: раз и два. Но вкратце напомню (подробнее можно почитать в [4,5]): каждый атом водорода/гелия имеет свою 1s орбиталь со своей энергией, которая пропорциональна —Z (где Z — заряд ядра), соответственно, у гелия (Z=2) 1s орбиталь находится ниже по энергии, чем у водорода (Z=1), поскольку последний притягивает электрон к себе в два раза сильнее, из-за чего его в два раза сложнее отодрать, чем от водорода.
Орбиталь сама по себе — это квантовое состояние, распределение всех положений, в которых может пребывать электрон, находясь около ядра. И когда у нас подходят два атома, допустим, A и B, достаточно близко друг к другу (под A и B могут скрываться как H так и He), электрон может двигаться в 1s состоянии вокруг первого ядра A, обозначим это квантовое состояние через кет-вектор |1sA⟩, а может двигаться в 1s состоянии вокруг второго ядра B, т.е. в |1sB⟩. Но ещё он может находиться в любых суперпозициях этих двух, т.н. базисных, состояний (как тот самый котэ Шрёдингера). Суперпозицию мы можем записать как сумму базисных состояний с произвольными коэффициентами
здесь cA и cB — это любые комплексные числа, такие что |cA|2+|cB|2=1 (в нулевом приближении). Причём случаи когда атом находится в состояниях |1sA⟩ или |1sB⟩ — это всего-лишь частные случаи этой записи (|ψ⟩), cA=1, cB=0, и cA=0, cB=1, соответственно.

И фишка в том, что если мы возьмём два атома, поставим их на не очень большое расстояние, и попробуем найти, в каком состоянии |ψ⟩ выгоднее всего энергетически находиться электрону (для этого нужно решить стационарное уравнение Шрёдингера), то окажется, что выгоднее всего быть в суперпозиции. Если два ядра у нас одинаковы, то, электрону, очевидно, нет разницы, около какого из ядер находиться, поэтому |cA|2=|cB|2=1/2. У нас получаются возможны два состояния, где орбитали каждого из атомов суммируются:
и где из одной вычитается другая:
Поскольку 1s-орбитали по форме похожи на шарики, то в первом случае (|ψ+⟩) получится, что электрон находится с большей вероятностью между двумя ядрами. В результате, он будет одновременно притягиваться к каждому из ядер, а заодно уменьшать отталкивание этих двух положительно заряженных частиц друг от друга, из-за чего получится выигрыш в энергии, относительно того, если бы атом находился около только одного из ядер. Такое состояние называется связывающей молекулярной орбиталью (МО). Название такое, поскольку это квантовое состояние соответствует тому, что электрон будет связывать два ядра, и именно это и есть источник химической связи. А молекулярная орбиталь — это именно потому что это то же самое распределение, квантовое состояние, только уже не для одного одинокого атома, а для целой молекулы. Второе состояние, |ψ—⟩, тоже является возможным, оно будет выше по энергии, чем |1sA⟩ и |1sB⟩. Причина та же: вычитание одной орбитали из другой, уменьшает вероятность нахождение электрона между ядрами, что приводит к тому, что те начинают отталкиваться ещё сильнее, в результате чего молекула разваливается. Поэтому аналогично |ψ+⟩, состояние |ψ—⟩ называется антисвязывающей (или разрыхляющей) молекулярной орбиталью (МО).
В случае же, если атомы A и B разного типа (что для нас означает только HHe), то очевидно более заряженное ядро (т.е. гелий) будет притягивать электрон сильнее, чем менее заряженное (т.е. водород), поэтому коэффициент |cHe|>|cH|, но в целом у нас будут те же две новые орбитали, связывающая и разрыхляющая МО, устроенные по тому же принципу (сумма и разность атомных орбиталей, соответственно).
Всё, устройство электронной оболочки самых главных молекул во Вселенной весьма простое. Дальше, если у нас имеется больше, чем один электрон, эти электроны заполняют связывающую и разрыхляющую орбиталь в соответствии с теми самыми правилами заполнения, которые мы учили в школе. На каждой орбитали может быть только два электрона, которые должны отличаться направлением спина. Заполняются орбитали в порядке возрастания энергии: сначала первые два электрона садятся на связывающую МО, а потом вторые возможные два — на разрыхляющую МО. В результате у нас будут получаться разные частицы. Как же понять, насколько они будут крепко связаны? Для этого можно посмотреть на величину порядка связи (или ПС). ПС — это просто разность числа электронов на связывающей МО (Nсв) и количества электронов на разрыхляющей МО (Nраз), делённое пополам:
Корреляция этой формулы с реальностью такая: чем больше электронов на связывающей орбитали, тем сильнее связь, чем больше на разрыхляющей — тем слабее. Ну и для образования одной ковалентной связи нам нужно два электрона, поэтому делим на двойку.
Вопрос который встаёт, когда мы говорим об образовавшейся молекуле: какое у нас будет расстояние между атомами, и что это за расстояние то такое? Собственно, у нас есть ядро A, это нечто размера порядка 10-15 метра, и ещё ядро B такого же порядка размеров. А молекула сама, на несколько порядков больше, 10-10—10-9 метра. Поэтому в реалиях молекулы, что ядра, что электроны мы можем считать маленькими точками. И вот о расстоянии между двумя точками, ядрами A и B мы и начинаем говорить при упоминании размера молекул (обозначим его буквой r). Когда мы думаем об образовании химических связей, мы по-сути говорим об энергии (E), которая будет зависеть от этого самого межатомного расстояния r., т.е. E=E(r). Энергия же эта собой будет являть сумму четырёх слагаемых:
-
энергии кулоновского отталкивания ядер друг от друга,
-
энергии кулоновского притяжения электронов к ядрам,
-
энергии кулоновского отталкивания электронов друг от друга (если электронов у нас больше одного),
-
и кинетической энергии электронов, т.к. электроны, маленькие квантовые частицы, на месте стоять не будут.
И для ядер, эта энергия будет являться потенциальной энергией, создаваемой движением электронов. Если мы построим эту E(r), для двухатомной молекулы она будет выглядеть как-то так:
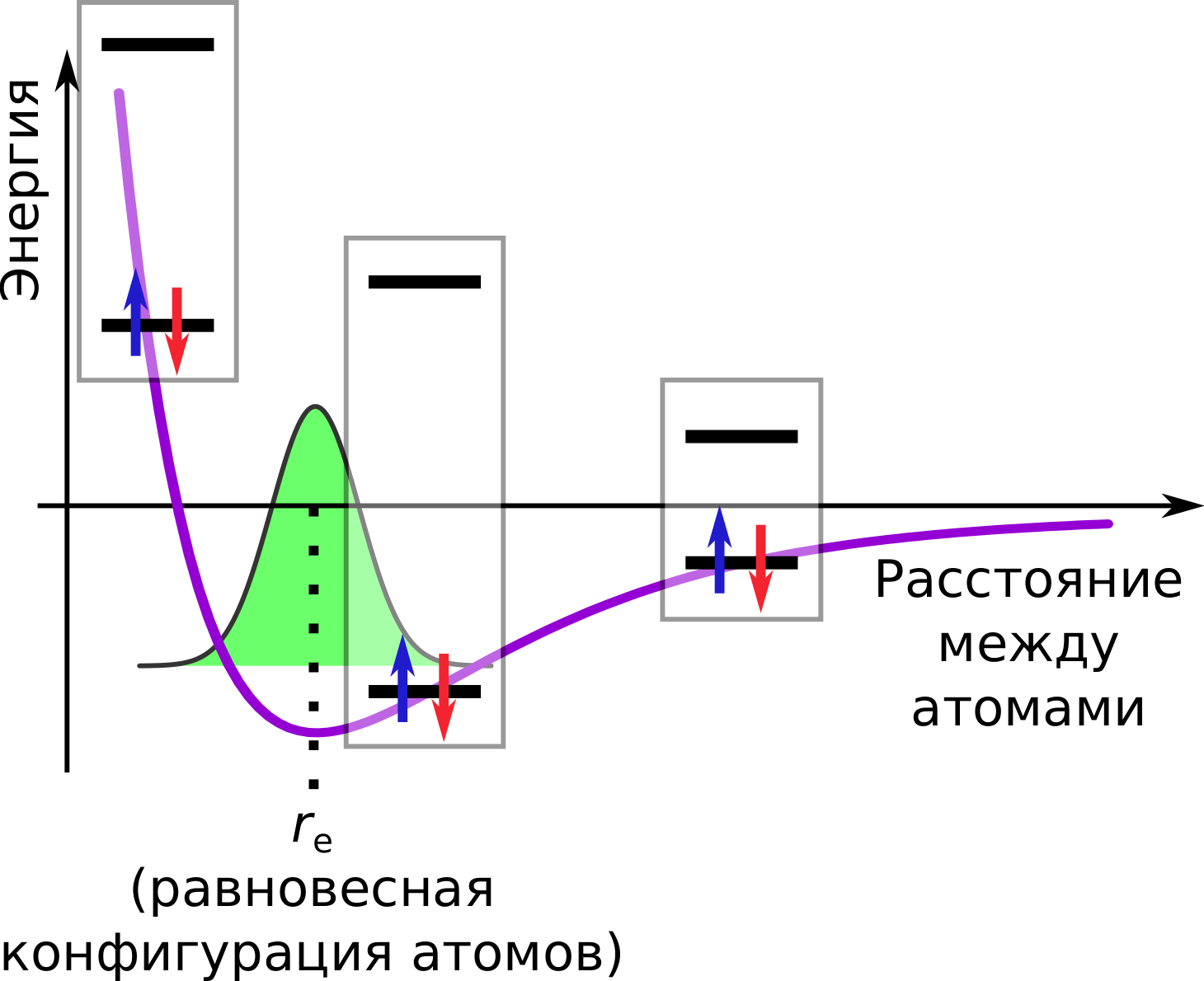
Справа (при больших r) потенциальная энергия стремится к какому-то значению, эта горизонтальная асимптота является энергией диссоциации (развала) молекулы AB на два атома, A и B. Слева, при r идущему к нулю у нас вертикальная асимптота, это кулоновское отталкивание двух положительно заряженных ядер. Если мы слишком близко приближаем ядра друг к другу, электронам становится банально мало места между ядрами, поэтому они меньше защищают их от отталкивания, поэтому и связывающая и разрыхляющая орбитали оказываются в целом уже не между ядрами, а вокруг обоих ядер одновременно. И вот между этими двумя асимптотами, у нас может быть (а может и не быть) минимум энергии. Расстояние re, соответствующее минимуму потенциальной энергии E называется равновесным расстоянием, и это расстояние и подразумевается когда мы говорим о размере молекулы. Конечно же, ядра тоже являются квантовыми частицами, поэтому находиться только в минимуме они не могут из-за того же принципа неопределённости Гейзенберга, поэтому они всё равно колеблются около равновесного расстояния туда-сюда, но тем не менее, далеко от этого расстояния они в среднем не уходят.
Оценить прочность молекулы AB мы можем посчитав выигрыш по энергии, который мы получаем в сравнении со случаем, когда у нас имеются два отдельных атома, A и B. На графике этот выигрыш выглядит очень просто: горизонтальная потенциальной энергии асимптота справа — это и есть сумма энергий отдельных атомов (EA и EB), т.е. E(r→∞)=EA+EB. Поэтому выигрыш энергии это просто
Если эту энергию сообщить молекуле AB (ядрам), то она развалится (или диссоциирует) на атомы A и B, поэтому De называется равновесной энергии диссоциации двухатомной молекулы.
Т.е. каждую двухатомную молекулу мы можем себе характеризовать в нулевом приближении двумя числами: равновесным межатомным расстоянием re, и её равновесной энергией диссоциации De, или какими-то аналогичными величинами.
Какими ещё аналогичными величинами?
Например, экспериментально проще определить эти же самые величины, где отсчёт идёт от усреднённого основного колебательного состояния ядер. Усреднённое таким образом межатомное расстояние зовётся r0, а отсчитанная от энергии нулевых колебаний энергия диссоциации обозначается как D0. Об этом я тоже писал, в своём первом посте на Хабре.
И эти две характеристики должны как-то коррелировать с ПС. По-идее, если у нас есть два атома, и мы меняем число электронов у этой частицы, то чем больше будет ПС, тем крепче связь, а значит re будет меньше, а De — больше. Но сожалению, это теоретическое предположение мы не можем проверить или без эксперимента, или без зубодробительной вычислительной квантовой механики, моделирующей молекулу из первых принципов. Поэтому…
Квантовая химия спешит на помощь
Раздел, моделирующий молекулы из первых принципов зовётся квантовой химией. По счастью, всё, что нам нужно, зашито в различные квантово-химические пакеты, и мой любимый — это Orca [6,7]. Скачать его бесплатно (для академического использования) можно с их форума [7], после простой и незамысловатой регистрации.
Для расчёта, помимо софта и выбора системы, придётся ещё выбрать т.н. приближение расчёта. Состоит приближение из двух частей: метод и базис. В детали я вдаваться не хочу (т.к. это огромная и сложная тема), но кратко попробую пояснить. Базис, по-сути — это численное представление орбиталей, их можно себе вообразить как набор атомных орбиталей, и чем больше их у нас есть в описании, тем точнее мы можем всё считать. В нашем случае я использовал экстраполяционную схему, основанную на расчётах в базисах cc-pVTZ/cc-pVQZ, или же просто развесистый базис aug-cc-pV6Z. С методом всё немного хитрее. Для систем с одним электроном (H2+) много думать не надо: они решаются точно вариационным методом (что можно получить в Орке, затребовав расчёт по методу Хартри-Фока). Если же электронов много, для точных вычислений приходится возиться с т.н. электронной корреляцией. Эта мифологическая сущность, по-сути, являет собой учёт сложных танцев, которые должны совершать электроны в попытке избежать друг друга при своих сложных передвижениях. И вот одним из самых точных методов учёта электронной корреляции является метод связанных кластеров, CCSD(T), называемый ещё «золотым стандартом квантовой химии». Что скрывается за ранее описанным, это большой и сложный вопрос, поэтому я просто оставлю это здесь.
Собственно, сами входные файлы для расчётов в Orca
Квантово-химические пакеты — это обычно числодробилки, не обременённые каким-либо GUI. Поэтому с юзером они общаются только при помощи командной строки и т.н. входных файлов (в простонародье, инпутов) — текстовых файлов, в которых даётся
-
информация о системе, которую нужно посчитать (какие атомы, где находятся, какой у них заряд, мультиплетность, и прочее),
-
информация о том, что нужно посчитать (энергию, найти равновесную геометрию, или что-то более сложное, типа разных спектров) и каким образом (те самые метод и базис),
-
часто там содержится технические аспекты расчёта (настройки распараллеливания, требование памяти у системы, и прочее),
-
ну и всё остальное что может понадобиться.
Orca — один из наиболее юзер-френдли квантово-химических пакетов, поэтому простейший файл для расчёта энергии атома гелия в хорошем приближении выглядит так:
! CCSD(T) Extrapolate(3/4) nori VeryTightSCF
%pal
nprocs 1 # number of processes in parallel execution
end
%maxcore 10000
* xyz 0 1
He 0.0 0.0 0.0
*Строки, начинающиеся с ! — это выбор метода и его настройки. CCSD(T) это тот самый метод связанных кластеров, Extrapolate(3/4) — это схема экстраполяции на базисах cc-pVTZ/cc-pVQZ, NoRI — это отключение ускорялки расчёта, методов разложения единицы, а VeryTightSCF — требование для повышенной точности нахождения электронной структуры в методе Хартри-Фока.
%pal — это секция для распараллеливания. У гелия одна электронная пара, а Орка не умеет параллелить CCSD(T) в больше процессов, чем число электронных пар. Поэтому nprocs 1 по-сути отключает параллельные вычисления для гелия. %maxcore — это число требуемой памяти на 1 процесс в мегабайтах. В данном случае хотим 10 гигов. Ну а *xyz — это собственно координаты молекулы. Цифры 0 и 1 — это соответственно заряд и мультиплетность частицы (у нас незаряженный синглет), а остальное — это просто декартовы координаты наших атомов в формате «<символ элемента>
Для получения кривых диссоциации нам нужно получить много точек, сделать скан. Такое можно провернуть при помощи такого вот инпута (для димера He2):
! CCSD(T) Extrapolate(3/4) nori VeryTightSCF
%pal
nprocs 2 # number of processes in parallel execution
end
%paras
x= 0.5,4.0,20
end
%maxcore 10000
* xyz 0 1
He 0.0 0.0 0.0
He {x} 0.0 0.0
*Тут мы просто сканируем значения параметра x в диапазоне от 0.5 до 4 Å, всего 20 точек. Для частиц с одним электроном CCSD(T) не начнёт работать, поэтому там просто заменяем это кодовое слово на флюгергехаймер HF (Хартри-Фок), а экстраполяционную схему на очень развесистый базис, например aug-cc-pV6Z.
И всё, дальше команда в *nix-овой системе:
[путь до экзешника]/orca [имя инпута] > [файл куда сохранятся результаты] &
отправляет нас в увлекательное ожидание окончания вычислений. А пока можно выпить чаю.
В результате работы компьютера, можно получить собственно, все интересующие нас параметры. Для начала, мы можем нарисовать все эти самые кривые потенциальной энергии для разных молекул, вот они какие красивые:
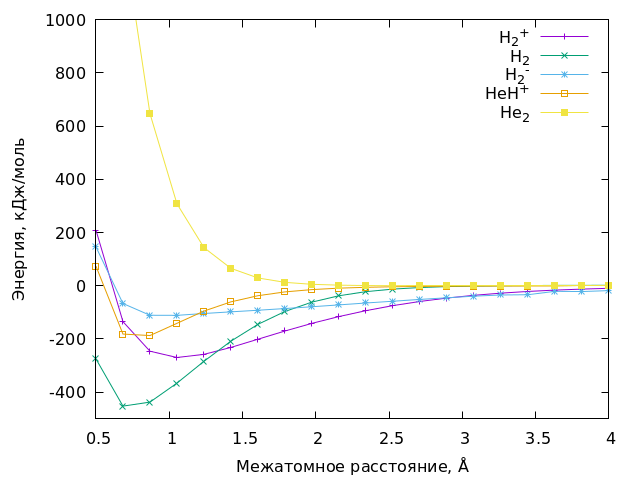
В качестве точки 0 для энергии на графике в каждом случае берётся энергия соответствующих изолированных атомов, например HeH+ разваливается на He и H+. (поскольку гелий держится за свои электроны крепче, чем водород), поэтому точкой отсчёта для иона HeH+ будет сумма энергий He и H+.
В результате мы можем посмотреть на корреляцию ПС с равновесными межатомными расстояниями молекул и их энергиями диссоциации. Собственно, они приведены в таблице ниже. В ней мы видим схемы того, как сидят электроны на связывающей и на разрыхляющей МО (МО и МО*, соответственно), а также получающиеся порядки связей (ПС), и равновесные расстояния (re) и энергии диссоциации (De).
|
|
H2+ |
H2 |
H2— |
HeH+ |
He2+ |
He2 |
|
МО* |
|
|
↑ |
|
↑ |
↑↓ |
|
МО |
↑ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
|
ПС |
1/2 |
1 |
1/2 |
1 |
1/2 |
0 |
|
re, Å |
1.10 |
0.75 |
1.03 |
0.77 |
1.08 |
3.26 |
|
De, кДж/моль |
295 |
463 |
96 |
203 |
233 |
0.04 |
Как мы видим, у всех частиц с половинчатым ПС (H2+, H2—, He2+) мы наблюдаем расстояния одного порядка (1-1.1 Å), в то время как для ПС=1 (H2 и HeH+) расстояние у нас порядка 0.7-0.8 Å. С энергиями диссоциации такого точного тренда по всем молекулам мы не видим, из-за большего числа факторов влияющих на эту величину. Но тем не менее, попарно, тенденция сохраняется: если у одной частицы ПС меньше, чем у другой, то и De тоже будет меньше.
В димере без химической связи (He2 с ПС=0) согласно тенденции у нас наблюдается совсем большое межатомное расстояние, 3.3 Å, и практически нулевая энергия диссоциации. Но тем не менее, минимум на кривой потенциальной энергии у нас всё равно присутствует. Причина его появления чуть более сложная, и виноваты в нём межмолекулярные слабые силы (ещё их называют Ван-дер-Ваальсовыми). О них можно почитать, например, тут: [8].
Почему так сложно сделать молекулу в Космосе?
Ну вроде кажется, почему бы просто всем атомам водорода, коих у нас так много в космосе летает, взять да и не соединиться друг с другом попарно, чтобы летать выгодно в виде молекул? Этому мешает очень много причин. Разберём их на примере образования молекул водорода по реакции H+H→H2.
Первая причина это ты весьма проста: Вселенная невероятно велика, и даже в тех регионах, где плотность газа выше (например, в газовых облаках, из которых потом образуются звёзды) вероятность одинокому атому встретить второй такой же одинокий атом, весьма мала.
Потом, если у нас есть два водорода, то при столкновении нам нужно, чтобы спины электронов были направленны в правильную (противоположную) сторону, т.к. если будут сталкиваться два водорода со спином вверх, то два этих электрона не смогут сесть на одну орбиталь из-за принципа запрета Паули (у электронов должно отличаться хотя бы одно квантовое число), в результате чего один электрон сядет на связывающую орбиталь, а второй на разрыхляющую, из-за чего химическая связь не сможет образоваться (ПС=(1-1)/2=0).
Ну и последняя, но не менее главная: при столкновении двух атомов у нас имеется избыток кинетической энергии, который нужно куда-то девать. Наша Вселенная живёт с очень строгой бухгалтерией, живущей по понятиям законам сохранения. И главный из этих законов — это закон сохранения энергии. Если у нас есть два атома, то у нас должна сохраняться полная энергия этой системы, которая состоит из кинетической энергии движения ядер (T) и потенциальной энергии, на которые мы уже насмотрелись в этом посте (E(r)). И если у нас эта суммарная энергия T+E превышает энергию диссоциации, то никакой молекулы у нас не образуется: два атома просто столкнутся, оттолкнутся друг от друга, и разлетятся навсегда в разные стороны. Так что для образования молекулы, когда атомы останутся рядом, эти атомы должны изначально не иметь кинетической столкновения энергии, например, лететь параллельно, и тогда когда-то они наконец когда-то далеко в будущем они притянутся друг к другу. Или же новообразованная почти-молекула может «сбросить» избыток кинетической энергии куда-то, чтобы образовалась молекула. По-сути, изначально у нас при столкновении имеется очень горячая система, и для охлаждения нам требуется нечто, куда сбрасывается избыток тепла. Таких вариантов у нас по-сути два: почти молекула может излучить фотон, или же столкнуться с третьим телом (атомом или молекулой), чтобы отдать ему избыток своей энергии. И тот и тот вариант на самом деле тоже не так уж вероятны.
Поэтому перемножая вероятности всех этих последовательных событий, мы понимаем, что каждая образованная в Космосе молекула — это невероятная случайность.
Как ищут молекулы в Космосе?
Естественно, можно полететь в космос, запихать туда сложную аппаратуру, типа масс-спектрометров, и увидеть все вещества, которые там есть, но пока что мы далеко из нашей солнечной системы такие приборы не смогли вывезти. Так как же узнать о том, что находится очень-очень-очень далеко от нас?
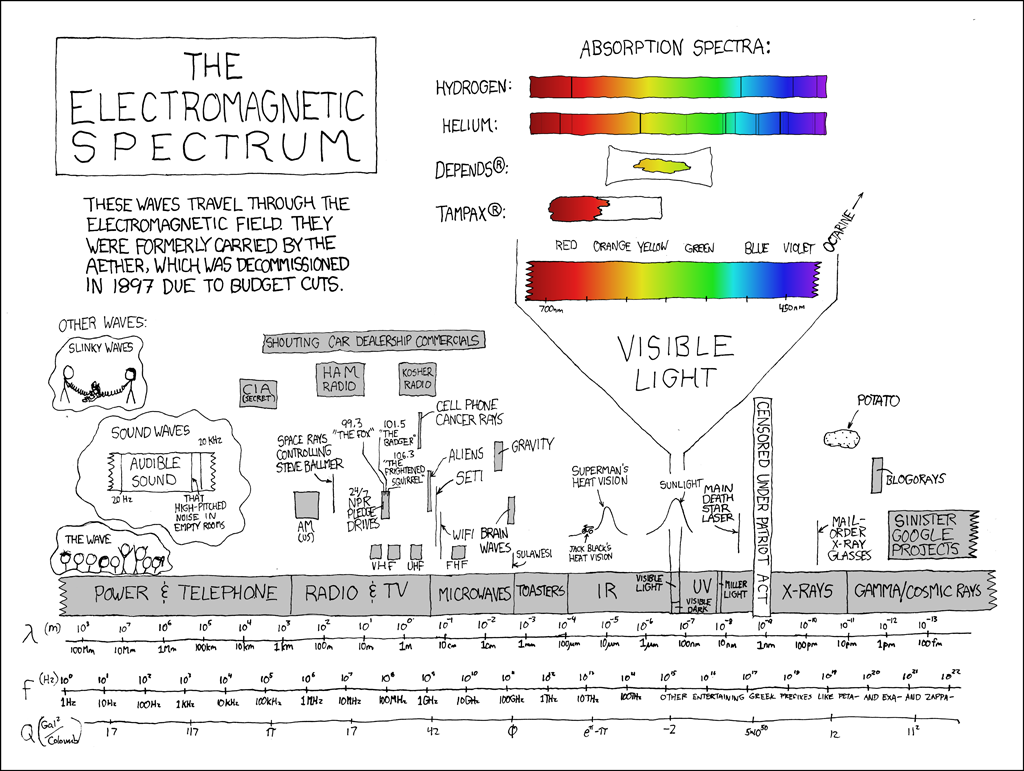
Ответ прост: спектроскопически, т.е. через электромагнитное излучение, которое приходит к нам из космоса. Например, как мы можем увидеть тот же водород или гелий в Солнце? Можно буквально взять призму и пустить через неё солнечный луч, в результате мы увидим, что в получающейся радуге будут тёмные полоски:
![Примерно так и выглядит линейчатый спектр Солнца, взято с [9], https://xkcd.com/1733/. Примерно так и выглядит линейчатый спектр Солнца, взято с [9], https://xkcd.com/1733/.](https://habrastorage.org/getpro/habr/upload_files/2f0/07d/268/2f007d2689e5f71dfac3099190dd9b43.png)
Горячий солнечный свет идёт через атомы, которые летают вокруг, и эти атомы поглощают излучение: происходит возбуждение электрона с одной орбитали на другую, в результате чего поглощается фотон определённой длины волны, и интенсивность света на этой длине волны падает. А поскольку для разных атомов орбитали имеют разные энергии, то эти полоски уникальным образом характеризуют соответствующие вещества.
Но электромагнитный спектр безграничен, поэтому для молекул в основном используется не видимый свет, а другие диапазоны: инфракрасный (ИК), микроволновый (МВ) и радио. Дело в том, что вращение молекул и их колебания гораздо более характеристично связаны со структурой молекул, и энергии соответствующих колебательных и вращательных переходов лежат в этих диапазонах частот. Конечно, не все молекулы можно так увидеть (в частности молекулярный водород фиг так поймаешь), но для новых молекул это гораздо лучше подходит. Например, недавно HeH+ нашли именно в терагерцовом диапазоне (это на границе ИК и МВ). [10]

Коснёмся немного и инструментария, которым ловят эти молекулы. ИК исследует в первую очередь колебания молекул, и это очень сложный диапазон для исследования на Земной поверхности… Дело в том, что в атмосфере нашей (кто б мог подумать) много всяких молекул, вода, углекислый газ, угарный газ и всякое такое. Поэтому когда ИК свет далёких галактик пронзает нашу атмосферу, эти самые компоненты сжирают его, и ничего дельного мы не видим. Поэтому для хорошего обзора ИК надо подниматься как можно выше, в горы, или, например, на самолёте. Для последнего у NASA есть ИК обсерватория SOFIA, сделанная на базе Boing-747. А для ещё лучшего отсутствия атмосферы, можно вообще улететь в космос! Spitzer, Herschel, WISE, ну и конечно же недавно запущенный Телескоп Джеймса Уэбба, они и предназначены для работы в том самом диапазоне.

Для радиоволн, микроволн и миллиметровых волн, дело на земной поверхности обстоит лучше: земная атмосфера имеет несколько окон «прозрачности», где компоненты атмосферы не так сильно портят космический сигнал. Поэтому с земли в космос вглядываются антенны различных радиотелескопов: РАТАН-600, Green Bank Telescope, ALMA, ну и не так давно это делал Аресибо.
Заключение
Рождение, жизнь (и смерть) молекул в космосе — это сложная и до сих пор до конца не изученная история. Очень много тайн нас ещё ждёт, например, то откуда и как взялись ходящие, говорящие и пишущие макромолекулярные системы, построенные на основе углеродных полимеров. Для этого мы отправляем к астероидам и другим планетам всякие сложные спутники и марсоходы, смотрим в небо в телескопы. Но для того, чтобы облегчить работу экспериментаторов, иногда приходится взять компьютер, вооружиться законами квантовой механики, да обсчитать какие-то молекулярные процессы, просто чтобы лучше взглянуть на них изнутри.
З.Ы. (рекламное)
Тем, кто изучает квантовую механику, и тем, кто хочет знать больше о том, как моделировать молекулы и понимать, что вообще там происходит на расстояниях порядка нанометров, я рекомендую недавно вышедшую в издательстве URSS книгу:
В ней много всякого интересного и полезного. Доступна она как в мягкой, так и твёрдой обложках.
З.З.Ы.: дополнительные материалы
Сырые данные с потенциальными энергиями (авось кому пригодится).
Здесь я дам сырые данные + скрипт, использованные для построения графика выше. Данные в формате <межатомное расстояние в Å> <энергия в Хартри>.
Ион H2+ в приближении HF/aug-cc-pV6Z:
0.50000000 -0.42034935
0.68421053 -0.55130244
0.86842105 -0.59360500
1.05263158 -0.60262958
1.23684211 -0.59809068
1.42105263 -0.58812825
1.60526316 -0.57641373
1.78947368 -0.56468245
1.97368421 -0.55375849
2.15789474 -0.54400899
2.34210526 -0.53555884
2.52631579 -0.52839968
2.71052632 -0.52244921
2.89473684 -0.51758554
3.07894737 -0.51366880
3.26315789 -0.51055575
3.44736842 -0.50810960
3.63157895 -0.50620627
3.81578947 -0.50473756
4.00000000 -0.50361181 Молекула H2 в приближении CCSD(T)/(3/4), 3/4 — это экстраполяция к полному базису на основе расчётов в базисах cc-pVTZ и cc-pVQZ:
0.50000000 -1.10460178
0.68421053 -1.17216571
0.86842105 -1.16643241
1.05263158 -1.13925734
1.23684211 -1.10801544
1.42105263 -1.07919981
1.60526316 -1.05522533
1.78947368 -1.03671598
1.97368421 -1.02335326
2.15789474 -1.01427530
2.34210526 -1.00840934
2.52631579 -1.00475562
2.71052632 -1.00253574
2.89473684 -1.00120795
3.07894737 -1.00041962
3.26315789 -0.99995105
3.44736842 -0.99967015
3.63157895 -0.99949992
3.81578947 -0.99939692
4.00000000 -0.99933615 Ион H2— в приближении CCSD(T)/(3/4):
0.50000000 -0.95512493
0.68421053 -1.03613322
0.86842105 -1.05297068
1.05263158 -1.05310619
1.23684211 -1.05049257
1.42105263 -1.04809555
1.60526316 -1.04583415
1.78947368 -1.04341314
1.97368421 -1.04081008
2.15789474 -1.03813033
2.34210526 -1.03545854
2.52631579 -1.03284171
2.71052632 -1.03033204
2.89473684 -1.02799670
3.07894737 -1.02565166
3.26315789 -1.02397490
3.44736842 -1.02354481
3.63157895 -1.01880709
3.81578947 -1.01910085
4.00000000 -1.01773954 Ион HHe+ в приближении CCSD(T)/(3/4):
0.50000000 -2.87567798
0.68421053 -2.97287701
0.86842105 -2.97499496
1.05263158 -2.95752599
1.23684211 -2.93997067
1.42105263 -2.92680218
1.60526316 -2.91805761
1.78947368 -2.91260851
1.97368421 -2.90928536
2.15789474 -2.90725113
2.34210526 -2.90600533
2.52631579 -2.90524905
2.71052632 -2.90479043
2.89473684 -2.90450687
3.07894737 -2.90432469
3.26315789 -2.90420212
3.44736842 -2.90411602
3.63157895 -2.90405342
3.81578947 -2.90400671
4.00000000 -2.90397117 Кластер He2 в приближении CCSD(T)/(3/4):
0.50000000 -4.78641295
0.68421053 -5.30204572
0.86842105 -5.56133624
1.05263158 -5.69041382
1.23684211 -5.75300095
1.42105263 -5.78268287
1.60526316 -5.79647854
1.78947368 -5.80275753
1.97368421 -5.80555626
2.15789474 -5.80678044
2.34210526 -5.80730495
2.52631579 -5.80752168
2.71052632 -5.80760591
2.89473684 -5.80763555
3.07894737 -5.80764378
3.26315789 -5.80764405
3.44736842 -5.80764170
3.63157895 -5.80763885
3.81578947 -5.80763627
4.00000000 -5.80763416 А вот и скрипт для Gnuplot. В нём мы вычитаем из абсолютных энергий каждой из молекул (отсчитывается от энергий стоящих ядер и электронов, находящихся на бесконечности) абсолютные энергии атомов, на которые она распадается:
set terminal pngcairo
set output "x2_pes_curve.png"
set xlabel "Межатомное расстояние, Å"
set ylabel "Энергия, кДж/моль"
Ha2kJmol=2625.5002
set xrange [0.5:4]
set yrange [-500.:1000.0]
# энергии атомов/ионов, на которые диссоциирует молекула
EHplus = 0.0
EH = -0.5
EHminus = -0.510794617778
EHeplus = -2.0
EHe = -2.90381370537
plot 'h2+.dat' u 1:(Ha2kJmol*($2-EH-EHplus)) w lp title "H_2^+",\
'h2.dat' u 1:(Ha2kJmol*($2-EH-EH)) w lp title "H_2",\
'h2-.dat' u 1:(Ha2kJmol*($2-EH-EHminus)) w lp title "H_2^-",\
'heh+.dat' u 1:(Ha2kJmol*($2-EHe-EHplus)) w lp title "HeH^+",\
'he2.dat' u 1:(Ha2kJmol*($2-EHe-EHe)) w lp title "He_2"-
1 — катион = положительно-заряженный ион
-
2 — анион = отрицательно-заряженный ион
Список литературы
-
Дуглас Адамс, Автостопом по Галактике. Ресторан «У конца Вселенной»
-
J. Chem. Phys. 152, 224108 (2020); https://doi.org/10.1063/5.0004608
-
Nature 568, 357–359 (2019); https://doi.org/10.1038/s41586-019-1090-x


