Что же это, чёрт возьми, такое, как работают нули-единицы, и кто и зачем это вообще придумал.
Начинаю серию статей с простым объяснением всяких фундаментальных вещей с иллюстрациями. Школьнику, которого учитель информатики заставляет переводить числа туда-сюда, а он вообще не врубается, что происходит. Дизайнеру, который не знает, что значит цвет #FFDD00. Тем, кто всё знает, но не против ещё раз укрепить модель.
В статье всё замаскировано под исторические события. Это фикция, я не знаю историю, поэтому придумал свою, чтобы было проще рассказывать.
Жил-был древний человек.

И были у него овцы.

И решил он однажды посчитать, сколько у него овец. Но считать ещё не умел.
Древний человек придумал оставлять засечки на камне. Одна засечка — одна овца. Когда рождается овца, человек рисовал засечку, когда умирала — стирал.
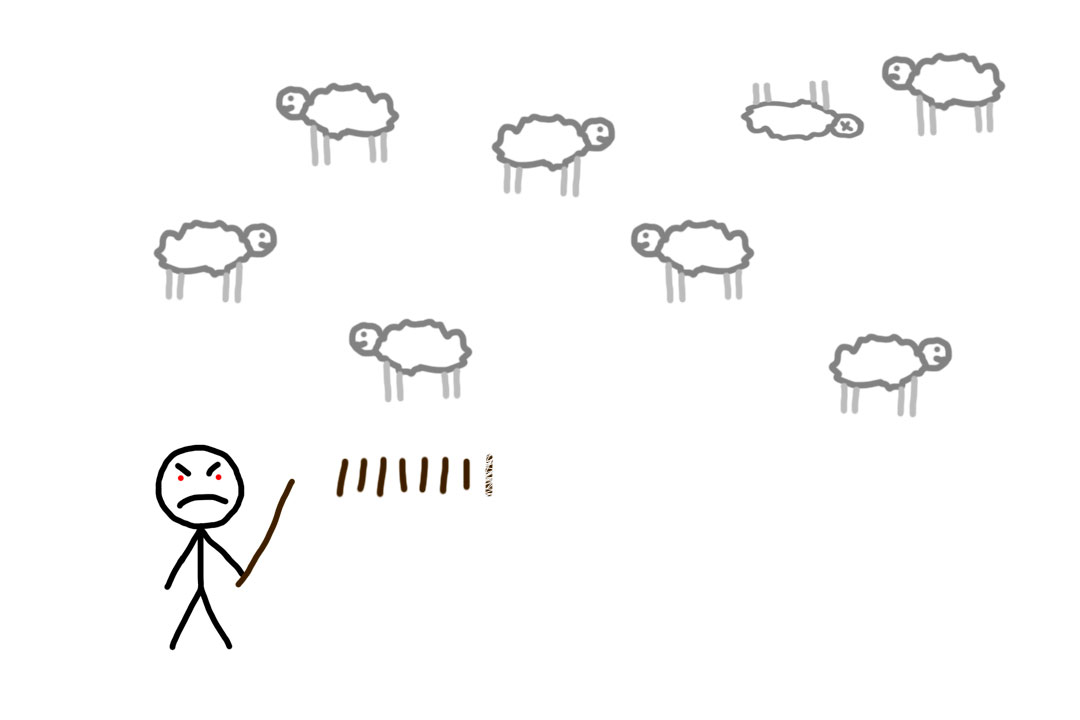
И жил так прекрасно древний человек, пока не поумнел и не решил узнать что-нибудь об окружающем его мире. И захотел он посчитать количество звёзд на небе — тем же способом.

И умер.
Это, конечно, такой естественный отбор был. Человек должен с копьём на кабана охотиться, а не звёзды считать.
Потом были древние римляне. Их было много, поэтому, очевидно, были те, кто поумнее, и все остальные. Последние охотились на кабана с копьём, а умные считали добычу и столкнулись с той же проблемой, что и древний человек.

И они подумали: «а давайте нарисуем ещё больше разных закорючек, и они будут кратко обозначать большие числа».
И придумали, что эти закорючки будут такими:
V = IIIII,
X = VV,
L = XXXXX,
C = LL,
D = CCCCC,
M = DD.
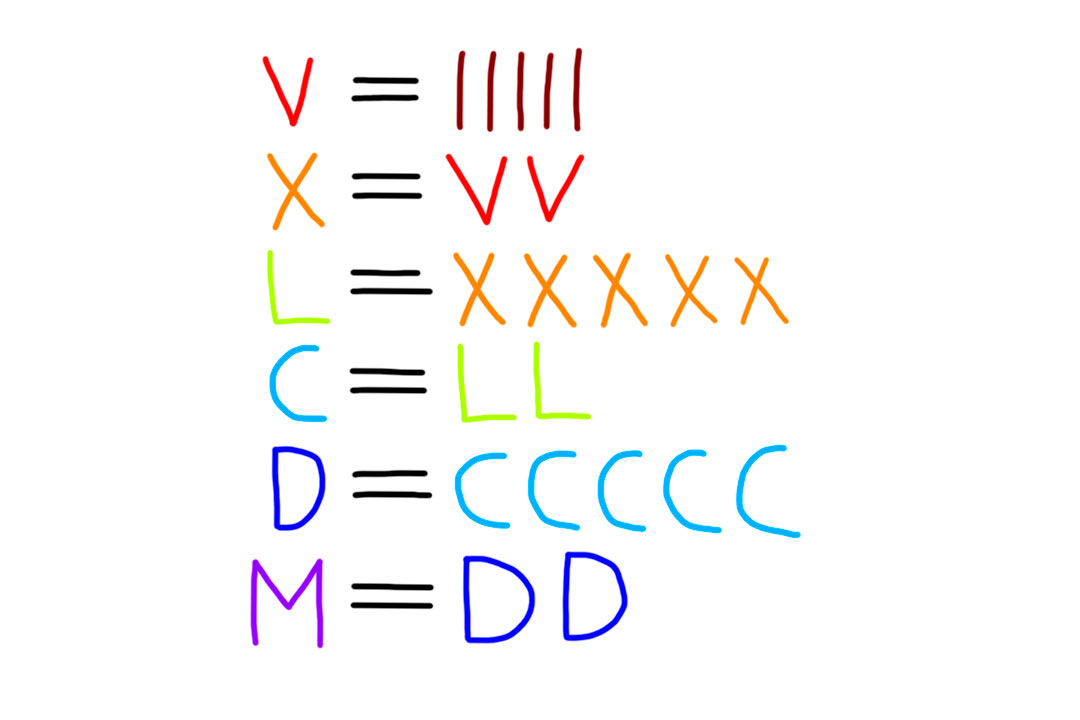
Ещё они придумали хитрые правила, чтобы, например, вместо VIIII писать IX, но для простоты повествования мы про эти правила забудем.
И смогли римляне посчитать, что средняя продолжительность жизни — лет L, а звёзд на небе видно примерно MMD. Им этого хватало.
Но время шло, и человечеству понадобилось записывать всё большие числа. Латинского алфавита, чтобы придумать ещё больше обозначений, не хватило бы, да и не очень это было удобно.
И нашёлся один умный человек, который придумал такую сложную и непонятную систему, что я не удивлюсь, если его за это потом сожгли.

Заметьте, что во всех предыдущих способах записи закорючки (цифры), стоящие рядом, просто складываются. Если древний человек написал II, это значит «I засечка и ещё I засечка». Если римлянин написал VII, это значит буквально IIIII + I + I, то есть IIIIIII.
Умный человек (горе ему) придумал вот что:
-
Пусть у нас будет сколько-то закорючек, например, X (здесь и дальше X — римская цифра, а не «неизвестное»). Позвал знакомого араба, сказал ему: «придумай мне X закорючек». Араб почесал репу и нарисовал: 0123456789.

-
Пусть 0 означает «ничего», а каждая следующая цифра сама по себе означает число, больше предыдущего на 1.
А дальше вообще отвал башки.
-
Пусть чем раньше в числе стоит цифра, тем большую «значимость» она имеет. Если цифра стоит в конце, она значит ровно столько, сколько написано. Если она на втором месте с конца, её собственное значение умножается на X. Если на третьем месте, то умножается на X и ещё раз на X, и так далее.
Например, если написано 456, то это значит не 4 + 5 + 6, а
4 * X * X + 5 * X + 6.
И понял умный человек, что цифра X ему больше особо и не нужна, потому что X — это 1 * X + 0, а значит записывается в новой системе как «10».
Ещё раз хочу обратить ваше внимание, насколько это неочевидная система — почему нужно ещё умножать цифры на что-то? почему нельзя просто, чтобы 4 значило 4? почему 4 в числе 456 обозначает 400? Но мы с вами выросли на этой системе, поэтому принимаем её за данность.
Таким образом, запись 456 означает 4 * 10 * 10 + 5 * 10 + 6. Какой-то другой умный человек придумал степени, и стало можно вместо 10 * 10 писать 10 ^ 2, вместо 10 * 10 * 10 писать 10 ^ 3 и так далее.

Немного терминологии, чтобы привязать знания к реальности.
-
Система счисления — это способ записывать количество какими-то чёрточками. Способ подсчёта овец древним человеком — система счисления. Запись чисел с помощью V, X и M римлянами — система счисления. Новый и прогрессивный способ, придуманный умным человеком, — тоже.
-
Непозиционная система счисления — та, где от положения цифры её значение не меняется. Древний человек придумал именно такую систему — I всегда значит I.
-
Позиционная система счисления — та, где, наоборот, положение цифры влияет на её значение. Такую систему изобрёл умный человек. Например, в числе 456 цифра 4 означает 400, а в числе 546 — всего 40.
-
Основание системы счисления — общее количество закорючек (цифр) в ней. Умный человек придумал систему счисления с основанием X (в этой системе, в свою очередь, X записывается как 10).
-
Разряд — положение цифры в числе.
Что будет, если изменить основание системы счисления, например, на 2?
В целом, то же самое, только: — цифры остались всего две — можем придумать любые, но для удобства обычно берут символы из нашей системы счисления. Например, у нас будут цифры 0 и 1. — возводить в степень мы будем уже не 10, а 2.
Переведём число 1010 из системы счисления с основанием 2 (то есть, из двоичной системы счисления) в нашу, десятичную. Чтобы не было путаницы, основание системы счисления обычно записывают после числа в нижнем регистре.
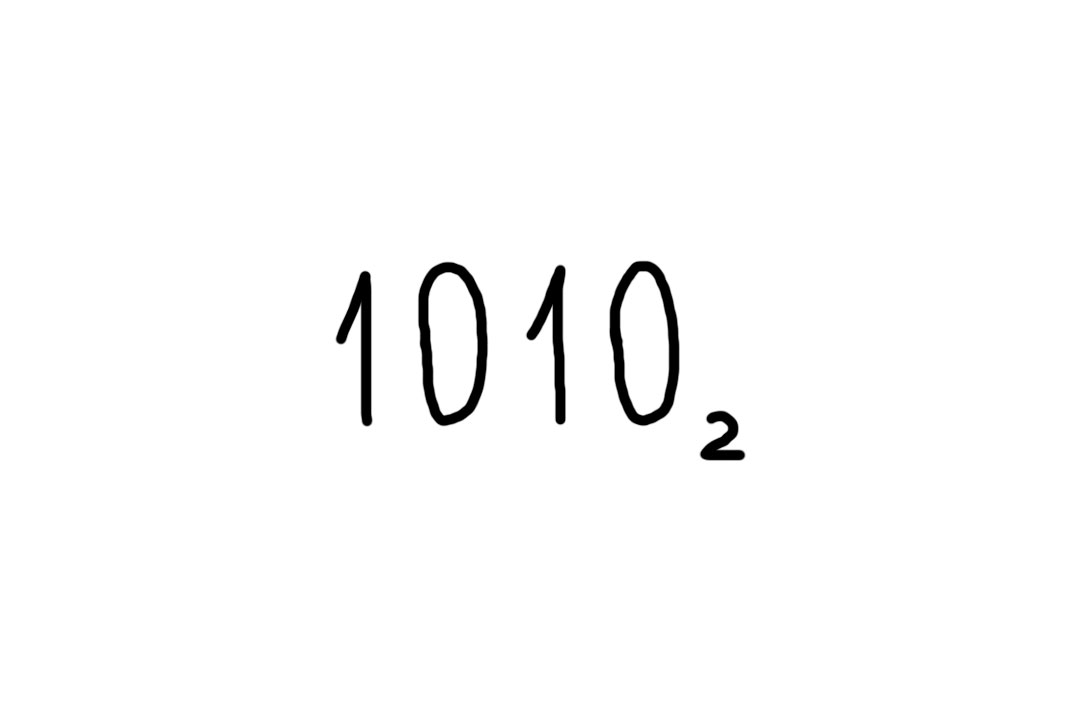
Пронумеруем разряды справа налево, начиная с нуля.
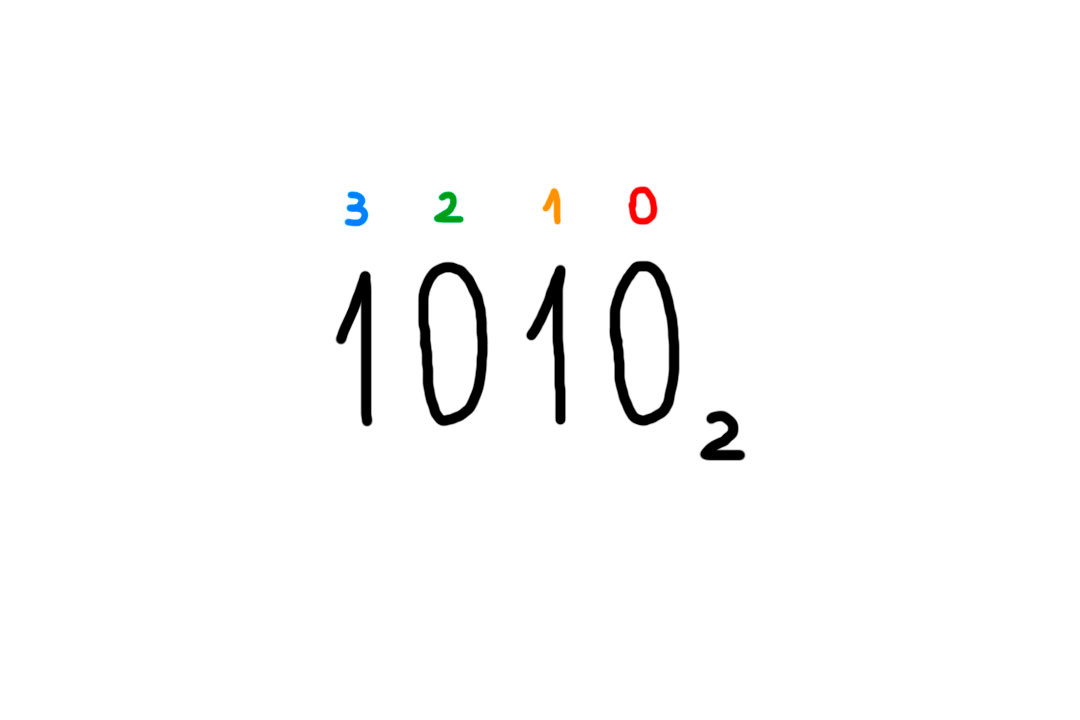
Тогда:
1010 = 0 * 2^0 + 1 * 2^1 + 0 * 2^2 + 1 * 2^3 = 0 + 2 + 0 + 8 = 10.
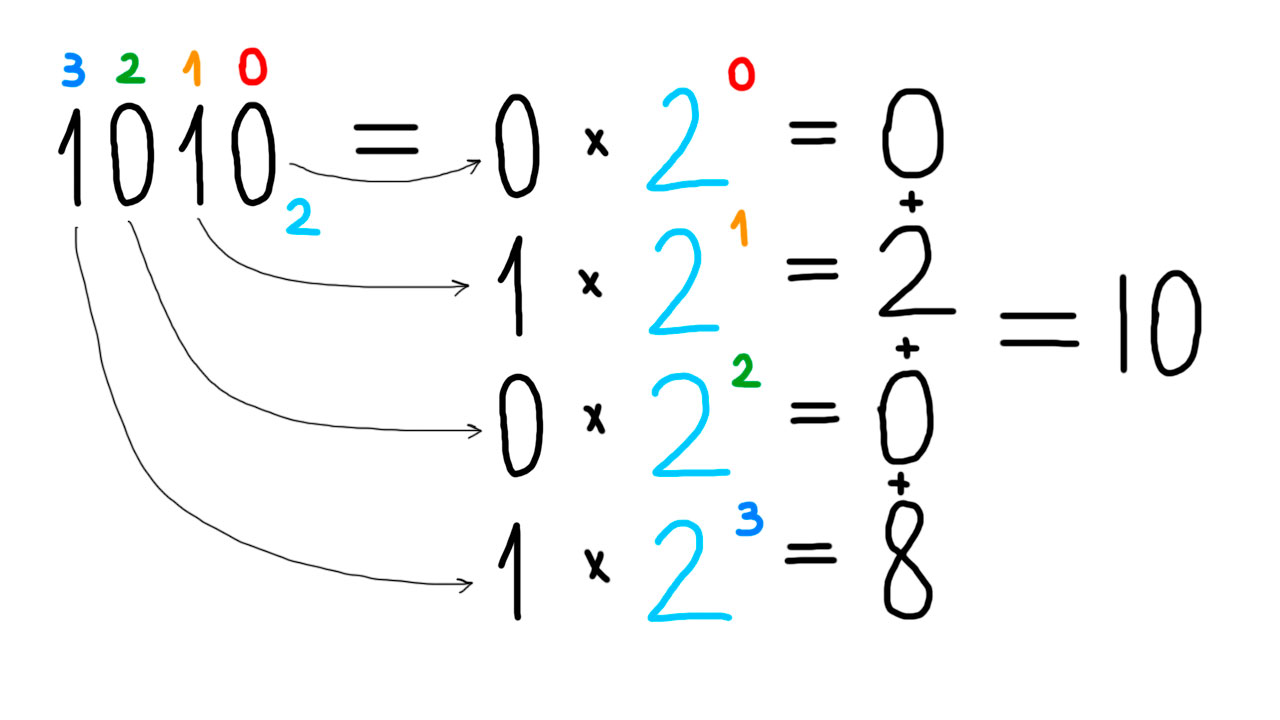
Выходит, 1010 в двоичной системе счисления обозначает такое же количество, какое 10 — в нашей, десятичной.
Двоичная система удобна, потому что в ней достаточно иметь всего две возможные позиции в каждом из разрядов — «ток течёт» или «ток не течёт», «палец загнут» или «палец выпрямлен».
Например, загибая пальцы рук, можно посчитать от 00000 00000 до 11111 11111, если принять левый мизинец за старший разряд, а правый мизинец — за младший, нулевой. Получается, в переводе на десятичную систему счисления на пальцах можно посчитать от нуля до 1023.
Первое, на что я хочу обратить внимание, — основание системы счисления в этой же системе всегда записывается как «10». В двоичной системе счисления число 2 записывается как «10», потому что 1 * 2 + 0 = 2. В шестнадцатеричной системе счисления число 16 записывается как «10», потому что 1 * 16 + 0 = 16. Ну вы поняли.
В связи с этим есть мем:

Инопланетянин говорит, что камней «10», потому что использует систему счисления с основанием 4 по-нашему. В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.
Кстати, про шестнадцатеричную систему счисления. Десять привычных нам цифр уже есть, а где ещё шесть взять? Да давайте просто возьмём ещё шесть букв. После 9 идёт A, потом B, потом C, D, E, F, и только потом — 10. Получается, что последние цифробуквы шестнадцатеричной системы счисления переводятся в десятичную так:
A = 10,
B = 11,
C = 12,
D = 13,
E = 14,
F = 15.
И последнее на сегодня — для дизайнеров. Что означает запись #FFDD00 для цвета? Наверняка вы знаете, что каждый пиксель на экране состоит из трёх лампочек — красного, зелёного и синего цвета, а все остальные цвета получаются смешиванием этих трёх в разной пропорции.
Каждая из лампочек может светить с условной яркостью от 0 до 255. #FFDD00 — это три числа: FF, DD и 00, где каждое число обозначает яркость каждой лампочки.
FF = 15 * 16 + 15 = 255.
DD = 13 * 16 + 13 = 221.
00 = 0.
Получается, красная лампочка включена на все 255, зелёная на 221, а синяя полностью выключена.

#FFFFFF — все лампочки горят на максимум и дают белый цвет. #000000 — все выключены, чёрный цвет.
Вот так, короче.
Следующая статья будет (наверное) про то, что такое, чёрт возьми, электричество, сила тока, чем она отличается от напряжения, что такое заряд, сопротивление и потенциал.
Подписывайтесь на меня в Твиттере: https://twitter.com/adam_arutyunov
А ещё есть канал — «Адам Арутюнов поднимается до мидла». В нём — вы не поверите. t.me/cdarr


