Первая часть теории Коллатца

28.04.2023

Аннотация

Эта первая статья из цикла «Доказательство гипотезы Коллатца», и на сегодняшний день единственная статья (в мире), раскрывающая истинную природу гипотезы Коллатца.
В этой статье автор подробно разбирает алгоритм гипотезы Коллатца, его структуру, свойства и особенности.

Ключевые слова: гипотеза Коллатца, алгоритм, рекурсия, шаг рекурсии, рекурсивный спуск, рекурсивный подъем.

§ 1. Постановка вопроса

Гипотеза Коллатца – это одна из нерешенных проблем математики. Получила широкую известность благодаря простоте формулировки.

Берём любое натуральное число ; Если оно чётное, разделим его на 2, а если нечетное, то умножаем на 3 и прибавляем 1 (получаем 3n+1); Над полученным числом выполняем те же самые действия, и так далее.

Какое бы начальное число мы ни взяли, рано или поздно мы получим единицу, – так гласит гипотеза. И надо это доказать.

§2. Введение

В математических кругах уже давно ходят легенды о недоказуемости этой задачи. Так, например, американский математик J. Lagarias вспоминает:
«В 1960-м более месяца весь Йельский университет безрезультатно трудился над проблемой 3n+1. Это было что-то невероятное. Такая же участь постигла и исследователей Чикагского университета, когда я сообщил им об этой задаче. Ходила шутка, что 3n+1 – это заговор советских ученых против США, чтобы снизить научный потенциал Америки и замедлить наши исследования в других областях.»

В 2007 г. математики S. Kurtz и J. Simon пришли к выводу, что в такой постановке вопроса задача 3n+1 не доказуема.
В 2010 г. Американское математическое сообщество выпустило сборник «Безграничный вызов для математики: 3x+1». Эта книга рассказывает о неудачных попытках найти решение для 3n+1.

Несмотря на всё это, автор, Михаил Мартынов, нашел в себе силы и раскрыл истинную суть гипотезы Коллатца. Поэтому данная статья является (на сегодняшний день) прорывом в области изучения и показывает, что гипотеза Коллатца – это всего лишь часть алгоритма. Для доказательства гипотезы Коллатца нам нужно перейти к совсем другой задаче.

§3. Полная версия алгоритма

Гипотеза выполняет действия 3n+1 и n / 2, тогда обратные действия: $\frac {n–1}{3}$ и * 2.
Сформулируем это так: Возьмем любое натуральное число ; Если оно нечетное, тогда умножаем на 2. Если чётное, тогда отнимем из него единицу ; Если результат деления $\frac {n–1}{3}$ будет целый, тогда это будет следующее число; Если нет, то умножаем на 2; И вообще, всегда умножаем на 2 для порождения всё новых и новых веток.

Посмотрим на последовательности по данной схеме:

1, 2, 4, 1
1, 2, 4, 8, 16, 5
1, 2, 4, 8, 16, 5, 10, 3
1, 2, 4, 8, 16, 5, 10, 20, 40, 13
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 7
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 7, 14, 28, 9
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 44, 88, 29, 58, 19

Обратим внимание, что это обычные последовательности Коллатца, только они развернуты в обратном направлении. Распишем всё это более подробно.

Выполним преобразование для 1:
Число 1. Умножаем на 2. Получаем 2.

Выполним преобразование для 2:
Число 2. Умножаем на 2. Получаем 4.

Выполним преобразование для 4:
Число 4. $\frac {4–1}{3} = 1$
Число 4. Умножаем на 2. Получаем 8.

Выполним преобразование для 8:
Число 8. Умножаем на 2. Получаем 16.

Выполним преобразование для 16:
Число 16. $\frac {16–1}{3} = 5$
Число 16. Умножаем на 2. Получаем 32.

Итак, мы на пороге первой развилки! 1, 2, 4, 8, 16 – здесь у нас развилка на 5 и 32.

Зайдем на развилку 5:
1, 2, 4, 8, 16, 5, 10 – здесь у нас снова развилка на 3 и 20.
1, 2, 4, 8, 16, 5, 10, 3, …
1, 2, 4, 8, 16, 5, 10, 20, …

Вернемся к числу 32:
1, 2, 4, 8, 16, 32, 64 – здесь у нас снова развилка на 21 и 128.
1, 2, 4, 8, 16, 32, 64, 21, …
1, 2, 4, 8, 16, 32, 64, 128, …

На этом остановимся.
Алгоритм, который мы только что описали – это рекурсия. Алгоритм воспроизводит действия $\frac {n–1}{3}$ , но только в обратном порядке. Таким образом, – это развернутая в обратном направлении рекурсия от рекурсии $\frac {n–1}{3}$ . Именно этим и обусловлен тот факт, что , повторяя зеркальные действия $\frac {n–1}{3}$ , спускается к единице.

Другими словами, рекурсия $\frac {n–1}{3}$ создала для нас дерево чисел. Рекурсия еще не знает, что это за дерево, но шагая по нему обречена спуститься до 1:

§4. Первые выводы

Во-первых, такой вид рекурсии в математике называется возвратная рекурсия или рекурсия пробега (см. книгу С.Клини, Введение в метаматематику, [гл. IX, §46]).
Во-вторых, как очевидно, рекурсия начинается с 1. Единица – прародитель всех веток.
В-третьих, спуск к единице для каждого числа происходит по своей уникальной ветке.
В-четвертых, единица не может иметь другого прародителя, кроме самого себя, потому что $\frac {n–1}{3}$ и дают для единицы – единицу (цикл 1, 4, 2, 1).
В-пятых, гипотеза Коллатца – это алгоритм, образованный от алгоритма $\frac {n–1}{3}$ , и поэтому сохраняющий все его свойства.

§5. Чётные числа

Шаг рекурсии $\frac {n–1}{3}$ кажется нам невероятно сложным из-за наличия чётных чисел. Но влияют ли они на рекурсию?
Давайте посмотрим на шаг рекурсии:

1
1, 2
1, 2, 4
1, 2, 4, 1
1, 2, 4, 8, 16
1, 2, 4, 8, 16, 5
1, 2, 4, 8, 16, 32
1, 2, 4, 8, 16, 5, 10
1, 2, 4, 8, 16, 5, 10, 3
1, 2, 4, 8, 16, 5, 10, 20, 40
1, 2, 4, 8, 16, 5, 10, 20, 40, 13
…

Применим бесконечное умножение на 2, и продолжим каждую последовательность:

Складывается впечатление, что чётные числа выполняют роль связующих между нечетными числами, а сам шаг основан только на нечетных.
Давайте это проверим.

§6. Нечётные числа

Пусть – нечетное число, тогда, чтобы двигаться вперед по правилу $\frac {n–1}{3}$ , мы должны:

Умножить *2, потому что – нечетное число.
Предположим, после находится нечетное число . Тогда справедливо равенство: $\frac {2n–1}{3} = x$
Получаем $x = \frac {2n–1}{3}$
Результат $\frac {2n}{3} – \frac {1}{3}$ будет целым только в том случае, если n ≡ 2 mod(3).

Тогда для n ≡ 1 mod(3) удвоим количество чётных чисел:

Умножаем на 2, и снова на 2.
Предположим, после находится нечетное число . Тогда справедливо равенство: $\frac {4n–1}{3} = x$
Получаем $x = \frac {4n–1}{3}$
Результат $\frac {4n}{3} – \frac {1}{3}$ всегда будет целый для n ≡ 1 mod(3).

§7. Хвост рекурсии

Обратим внимание, что получив на любом шаге нечетное число вида n ≡ 0 mod(3), мы не сможем продолжить генерацию чисел $\frac {2n–1}{3}$ , или $\frac {4n–1}{3}$ , или $\frac {8n–1}{3}$ , или $\frac {16n–1}{3},$ или любой другой степени двойки .
Потому что если n ≡ 0 mod(3), то решение уравнения $(\frac {2^kn}{3} – \frac {1}{3})$ сводится к виду: $2^kz – \frac {1}{3}$ . Оно не имеет целочисленного решения.
Числа вида n ≡ 0 mod(3) мы будем называть хвостом рекурсии.

§8. Особая связь ()

Алгоритм $\frac {n–1}{3}$ подразумевает постоянное умножение на 2.
Чтобы мы ни делали, мы всегда умножаем на 2. Именно в этом кроется ответ на вопрос, почему все нечетные числа в последовательностях Коллатца отделены друг от друга чётными.
В таком случае возникает ситуация, когда нечетное число может дать нам сразу две ветки нечетных чисел (как на рисунке выше). Т.е. нечетное число «раздваивается» на два нечетных числа.

Первый случай

Как мы уже выяснили, если существует такое нечетное число n ≡ 2 mod(3), то из этого следует, что также существует нечетное число $x = \frac {2n–1}{3}$ .
Но если мы умножим на 8, то обязательно будет существовать число: $y = \frac {8n–1}{3}$ . Потому что любое число n ≡ 2 mod(3) можно представить как , тогда уравнение $y = \frac {8n–1}{3}$ сводится к решению:

$y = \frac{8(3k–1)–1}{3} = \frac{24k–9}{3}=8k–3$ , что, конечно, имеет целочисленное решение.

Есть ли связь между полученными таким образом числами: и ?

$x = \frac {2n–1}{3}, \; \; n = \frac {3x+1}{2}$

$y = \frac {8n–1}{3}, \; \; n = \frac {3y+1}{8}$

$\frac {3x+1}{2} = \frac {3y+1}{8}$

Да, связь есть.
Другими словами, из нечетного числа n ≡ 2 mod(3) мы можем получить сразу два числа, число $x = \frac {2n–1}{3}$ и число

Второй случай

Как мы уже выяснили, если существует такое нечетное число n ≡ 1 mod(3), то из этого следует, что также существует и нечетное число $x = \frac {4n–1}{3}$ .
Но если мы умножим на 16, то обязательно будет существовать число: $y = \frac {16n–1}{3}$ . Потому что любое число n ≡ 1 mod(3) можно представить как , тогда уравнение $y = \frac {16n–1}{3}$ сводится к решению:

$y = \frac{16(3k–2)–1}{3} = \frac{48k–33}{3}=16k–11$ , что, конечно, имеет целочисленное решение.

Есть ли связь между полученными таким образом числами: и ?

$x = \frac {4n–1}{3}, \; \; \; n = \frac {3x+1}{4}$

$y = \frac {16n–1}{3}, \; \; n = \frac {3y+1}{16}$

$\frac {3x+1}{4} = \frac {3y+1}{16}$

Да, связь есть.
Другими словами, из нечетного числа n ≡ 1 mod(3) мы можем получить сразу два числа, число $x = \frac {4n–1}{3}$ и число

Таким образом мы установили шаг рекурсии между всеми нечетными числами:

$\frac{2n–1}{3}$ для случая n ≡ 2 mod(3),

$\frac{4n–1}{3}$ для случая n ≡ 1 mod(3),

для случая n ≡ 0 mod(3),
и постоянное применение к уже полученным числам .

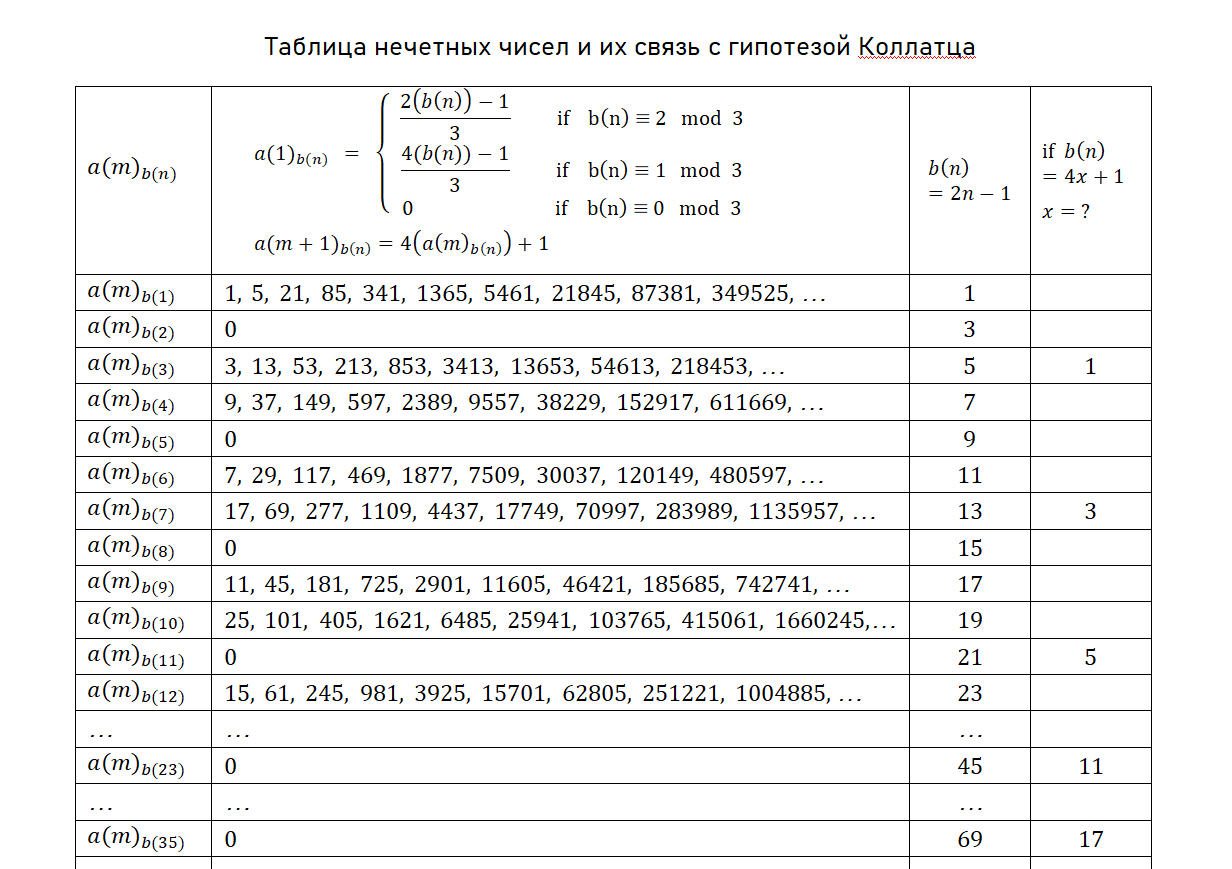
§9. Новый алгоритм

Мы выкинули все чётные числа из рекурсии, и упростили алгоритм до применения всего лишь трех правил $\frac{2n–1}{3}$ , $\frac{4n–1}{3}$ и . Распишем всё это более подробно.

Итерация №1.
Число 1. n ≡ 1 mod(3), применяем $\frac{4n–1}{3}, \quad \frac {4–1}{3} = 1.$
Число 1. 4n+1 = 5.

Итерация №2.
Число 5. n ≡ 2 mod(3), применяем $\frac{2n–1}{3}, \quad \frac {10–1}{3} = 3.$
Число 5. 4n+1 = 21.

Итерация №3.
Число 3. n ≡ 0 mod(3), хвост рекурсии.
Число 3. 4n+1 = 13.

Итерация №4.
Число 13. n ≡ 1 mod(3), применяем $\frac{4n–1}{3}, \quad \frac {52–1}{3} = 17.$
Число 13. 4n+1 = 53.

Итерация №5.
Число 17. n ≡ 2 mod(3), применяем $\frac{2n–1}{3}, \quad \frac {34–1}{3} = 11.$
Число 17. 4n+1 = 69.

Итерация №6.
Число 11. n ≡ 2 mod(3), применяем $\frac{2n–1}{3}, \quad \frac {22–1}{3} = 7.$
Число 11. 4n+1 = 45.

Итерация №7.
Число 7. n ≡ 1 mod(3), применяем $\frac{4n–1}{3}, \quad \frac {28–1}{3} = 9.$
Число 7. 4n+1 = 29.

и т.д.

§10. Как получить число 27?

С точки зрения рекурсии $\frac {n–1}{3}$ ей без разницы какое число связано с каким.
С точки зрения людей, они любят придумывать аномалии.

Для того чтобы получить число 27 нам нужно просто запустить рекурсию из единицы и прогуляться по следующей ветке:

1 $\rightarrow$ 5 $\rightarrow$ 3 $\rightarrow$ 13 $\rightarrow$ 53 $\rightarrow$ 35 $\rightarrow$ 23 $\rightarrow$ 15 $\rightarrow$ 61 $\rightarrow$ 81 $\rightarrow$ 325 $\rightarrow$ 433 $\rightarrow$ 577 $\rightarrow$ 769 $\rightarrow$ 3077 $\rightarrow$ 2051 $\rightarrow$ 1367 $\rightarrow$ 911 $\rightarrow$ 607 $\rightarrow$ 2429 $\rightarrow$ 1619 $\rightarrow$ 1079 $\rightarrow$ 719 $\rightarrow$ 479 $\rightarrow$ 319 $\rightarrow$ 425 $\rightarrow$ 283 $\rightarrow$ 377 $\rightarrow$ 251 $\rightarrow$ 167 $\rightarrow$ 111 $\rightarrow$ 445 $\rightarrow$ 593 $\rightarrow$ 395 $\rightarrow$ 263 $\rightarrow$ 175 $\rightarrow$ 233 $\rightarrow$ 155 $\rightarrow$ 103 $\rightarrow$ 137 $\rightarrow$ 91 $\rightarrow$ 121 $\rightarrow$ 161 $\rightarrow$ 107 $\rightarrow$ 71 $\rightarrow$ 47 $\rightarrow$ 31 $\rightarrow$ 41 $\rightarrow$ 27.

§11. Реализация рекурсии на компьютере

Рекурсия является простейшей, с точки зрения реализации. Для генерации новых чисел нужно рекурсивно выполнять следующий кусок кода, начиная с единицы:

Процедура ПрименитьПравила(n)
    
	Если (n % 3 = 1) Тогда
		ПервоеЧисло = (4*n - 1)/3;
		ВтороеЧисло = 4*n + 1;
	КонецЕсли;
	
	Если (n % 3 = 2) Тогда
		ПервоеЧисло = (2*n - 1)/3;
		ВтороеЧисло = 4*n + 1;
	КонецЕсли;

	Если (n % 3 = 0) Тогда
		ПервоеЧисло = 0; // хвост рекурсии
		ВтороеЧисло = 4*n + 1;
	КонецЕсли;
	
	ДобавитьНовоеЗначениеВТаблицу(ПервоеЧисло);
	ДобавитьНовоеЗначениеВТаблицу(ВтороеЧисло);
	
КонецПроцедуры

Для покрытия интервала от [1 … 100] требуется 500 итераций.
Для покрытия интервала от [1 … 1000] требуется 25000 итераций.
Для покрытия интервала от [1 … 10000] требуется 1 млн. итераций.

С уважением,
Автор статьи: Михаил Мартынов

Источник