
Сколько бы самолетов человек ни создал, истинными покорителями неба все равно останутся птицы. Человек «прикоснулся» к облакам всего лишь пару сотен лет тому назад, в то время как птицы на протяжении тысяч лет рассекают небеса. И секрет их заключается в долгой и скрупулезной эволюции, которая должна была учесть все аспекты, тем или иным образом влияющие не только на саму возможность летать, но и на качество полета. Глядя в небо, особенно безоблачное, кажется, там царит тишь да гладь. Однако множество воздушных потоков, которые меняют свое направление и скорость, создают ряд трудностей, с которыми птицы должны справляться. Наблюдая за полетом птицы, можно увидеть и продолжительное планирование без едино взмаха, и фигуры высшего пилотажа. Ученые из университета Британской Колумбии (Канада) и Мичиганского университета (США) установили, что птицы способны переходить от устойчивого полета к неустойчивому (и обратно) посредством изменения морфологии своих крыльев. Как именно происходит такой переход, чем он контролируется, и как полученные данные можно применить в авиастроении? Ответы на эти вопросы мы найдем в докладе ученых. Полетели. Поехали.
Основа исследования
Прежде всего стоит прояснить некоторые аспекты, связанные со стабильным (устойчивым) и нестабильным (неустойчивым) режимами полета. В первом случае птица просто планирует по воздуху, не совершая каких-то особенных телодвижений. Во втором — движения есть, при этом они зависят как от внешних факторов (скорость и направление воздушного потока), так и от внутренних (аэродинамические и инерционные свойства самой птицы).
Чтобы совершать свои удивительные маневры, которые регулируются специфическими для птиц уравнениями движения, птицы в нужный момент меняют форму крыльев. Для решения этих уравнений требуется информация об аэродинамических и инерционных характеристиках птицы. Как отмечают ученые, аэродинамика птиц не обделена вниманием со стороны научного сообщества, чего нельзя сказать об инерционных свойствах, таких как центр тяжести* и момент инерции*.
Центр тяжести* — точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю.
Момент инерции* — мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.
В рассматриваемом нами сегодня труде ученые использовали аналитический метод определения инерционных характеристик 22 видов птиц по всему диапазону сгибания и разгибания локтя и запястья. Было обнаружено, что трансформация крыльев позволяет птицам существенно изменять инерцию крена и рыскания, но оказывает минимальное влияние на положение центра тяжести. С добавлением инерционных характеристик была получена новая метрика маневренности по тангажу и проведена оценка статической устойчивости по тангажу. В результате было обнаружено, что диапазоны маневренности и статического запаса* уменьшаются по мере увеличения массы тела.
Статический запас* — понятие, используемое для характеристики статической продольной устойчивости и управляемости самолета, ракеты или (в данном случае) птицы.
Полученные в ходе данные говорят о том, что с точки зрения эволюции не было уклона в сторону устойчивого или неустойчивого полета, а был уклон в сторону развития способности перехода между этими двумя состояниями. Также результаты анализа позволили создать более полную картину маневренности птиц и характеристик, влияющих на нее.
Ученые отмечают, что на данный момент нет теории, которая могла бы полностью пояснить все аспекты маневренности птиц. Так получается не из-за отсутствия физического понимания, ибо маневренность можно в широком смысле определить как способность птицы изменять величину и направление вектора своей скорости. Подобно сопоставимым беспилотным летательным аппаратам, динамика полета птицы и, следовательно, ее маневренность диктуются ее основными уравнениями движения.
Например, динамика самолета зависит как минимум от шести уравнений, трех поступательных и трех вращательных, которые можно вывести из второго закона Ньютона и его вращательного аналога:

где v — вектор скорости, а ω — вектор угловой скорости.
Эти уравнения можно комбинировать для определения ускорения летательного аппарата (поступательное: dv/dt; вращательное: dω/dt), но для этого требуется знание как аэродинамически обоснованных внешних сил (F) и моментов (M), так и инерционных характеристик, включая массу (m) и тензор момента инерции (I). Проблема в том, что именно инерционные характеристики птиц на данный момент изучены плохо.
Таким образом, маневренность птиц в полете часто оценивают экспериментально, отслеживая особей для измерения ускорений во время наблюдаемых маневров. Но такие наблюдения не позволяют оценить максимальные маневренные возможности птицы. Для определения этих характеристик требуется надежная и общая основа для маневренности, эквивалентная уравнениям маневренности для самолетов. Получение обобщающих данных еще более осложняется тем, что аэродинамические и инерционные характеристики существенно различаются внутри и между видами и даже динамически у одной и той же птицы в зависимости от обстоятельств.
Например, птицы могут инициировать маневры, трансформируясь, то есть изменяя ориентацию и форму своих крыльев, тела и хвоста. Опять же, чтобы приблизиться к полному пониманию маневренности птиц, был сделан заметный и оправданный акцент на определении аэродинамических характеристик птицы в полете. Но инерционные свойства (1а) опять остались в стороне. Посему авторы рассматриваемого нами сегодня труда и решили исправить этот недочет своих предшественников.
Результаты исследования
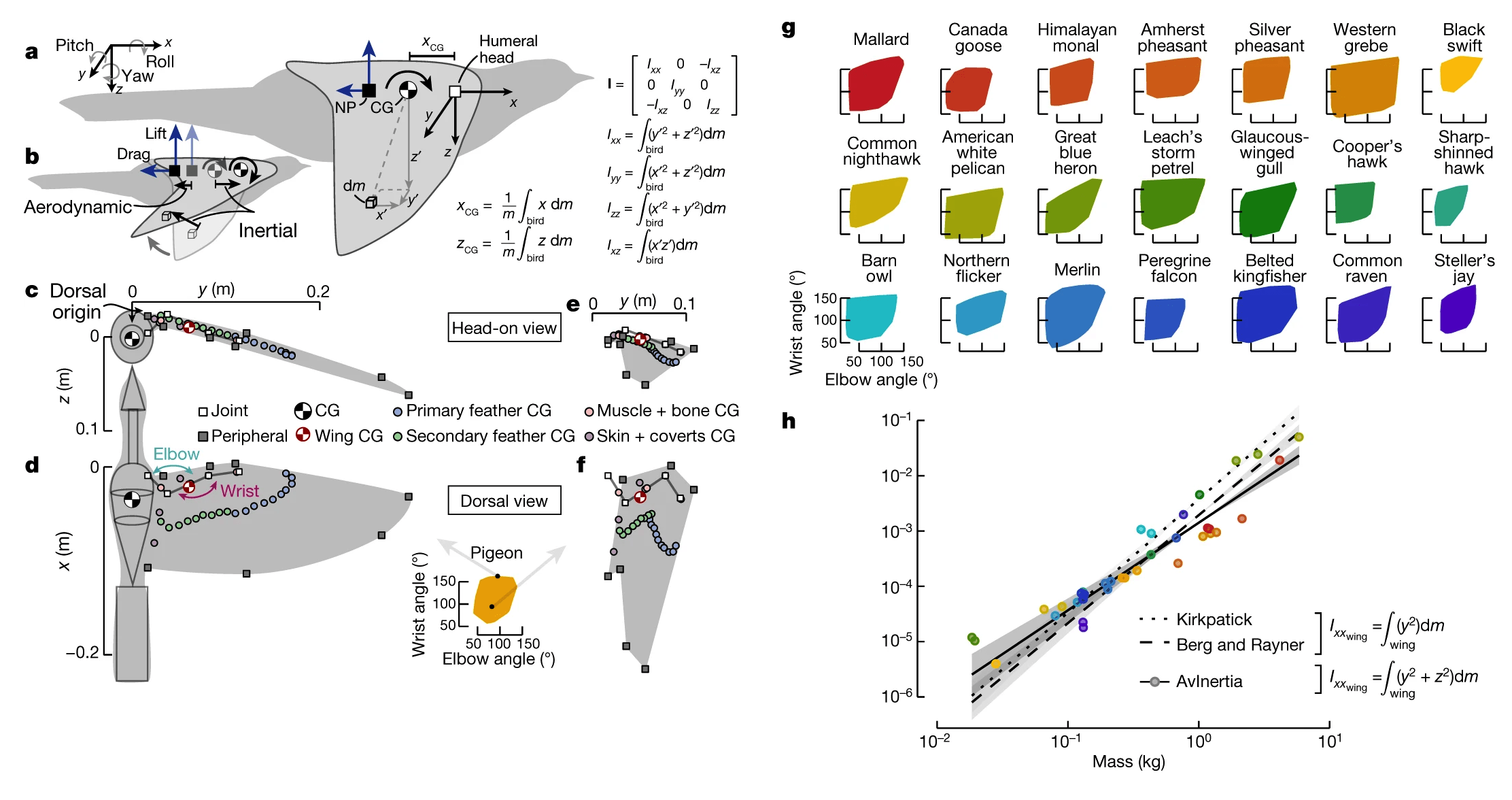
Изображение №1
Еще одна проблема при решении уравнений движения летящей птицы заключается в том, как правильно сформулировать уравнения. Например, уравнения можно упростить, определив начало координат в центре тяжести (1а), что эквивалентно центру масс в постоянном гравитационном поле.
Если центр тяжести существенно перемещается относительно тела, для правильного отражения динамики полета требуются дополнительные члены в уравнениях. Физическое изменение морфологии птицы смещает центр тяжести, но неизвестно, насколько центр тяжести перемещается по мере изменения формы птицы. Кроме того, морфинг (трансформация) также влияет на инерцию вращения, количественно определяемую моментом массы тензора инерции* (I) относительно начала координат (1a и 1b).
Тензор инерции* — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с угловой скоростью.
Эта симметричная матрица описывает распределение массы тела, где диагональные элементы количественно определяют распределение относительно основных осей (Ixx — крен; Iyy — тангаж и Izz — рыскание), а внедиагональные элементы количественно определяют распределение в трех основных геометрических плоскостях (только Ixz отличен от нуля для симметричных конфигураций).
Рыскание* — угловые движения объекта относительно вертикальной оси.
Крен* — поворот объекта вокруг его продольной оси.
Тангаж* — угловое движение объекта относительно главной (горизонтальной) поперечной оси.
Далее были рассчитаны центр тяжести и I, чтобы оценить ее маневренность через призму подвижности и статической устойчивости. Подвижность включает в себя способность птицы выполнять линейные ускорения (осевая маневренность) и угловые ускорения (торсионная маневренность) и зависит как от центра тяжести, так и от I. Напротив, статическая устойчивость относится к первоначальной тенденции вернуться к равновесию после возмущения.
Статическая устойчивость была количественно определена по тангажу с помощью статического запаса, который представляет собой расстояние между центром тяжести и нейтральной точкой (1а). Если нейтральная точка находится за центром тяжести, статический запас будет положительным и, следовательно, стабильным. Часто устойчивость обратно пропорциональна маневренности, так как иногда необходимы большие маневренные силы и моменты для преодоления стабилизирующих сил и моментов.
Чтобы определить, как изменяются инерционные характеристики во время морфинга крыла, ученые разработали общий аналитический метод для количественной оценки центра тяжести и I любой летающей птицы. После чего использовали сравнительный анализ для исследования 22 видов птиц (2a).
В первую очередь были измерены геометрические и массовые свойства тел, а также оценены диапазоны разгибания и сгибания локтя и запястья (1g). Ученые объясняют, что особое внимание морфингу крыльев было уделено, потому что предыдущие исследования показали, что этот диапазон движения (ROM от range of motion) обеспечивает существенное смещение нейтральной точки. Исследуемый ROM определяет физическую способность птицы регулировать свои инерционные характеристики и включает в себя конфигурации крыльев, отличные от тех, которые, вероятно, используются в полете.
Дополнительно был разработан пакет инструментов с открытым исходным кодом (Avinertia), который моделирует птиц как составную структуру простых геометрических объектов и использует морфологические данные для расчета центра тяжести и I для любой птицы с любой конфигурацией крыла (1c—1f). Данная методология была подтверждена предыдущими статическими измерениями крыла (1h).

Изображение №2
Получив подтвержденные результаты, ученые первым делом проверили влияние ROM локтей и запястий на центр тяжести птицы, когда ее крылья удерживаются симметрично. Было обнаружено, что ROM оказывает минимальное влияние на положение центра тяжести (2b).
Максимальные смещения по оси x и оси z (xCG и zCG) составили: 3% или 2.0 см — Ardea herodias (большая голубая цапля); 2% или 0.7 см — Tyto alba (сипуха). Несмотря на небольшую величину, разгибание запястья постоянно сдвигало xCG вперед (P < 0.002), а угол запястья объяснял большую дисперсию данных, приводящую к высокому размеру эффекта, количественно определяемому частичным η2*. Было установлено, что частичный η2 был больше 0.34 для всех видов (2e).
Частичный η2* — способ измерения размера эффекта различных переменных в моделях ANOVA (дисперсионный анализ). Он измеряет долю дисперсии, объясняемую данной переменной, в общей дисперсии, оставшейся после учета дисперсии, объясняемой другими переменными в модели.
Точно так же разгибание локтя имело тенденцию смещать xCG вперед, но величина его эффекта различалась у разных видов. Разгибание локтя и запястья преимущественно смещало zCG дорсально, но величина и размер эффекта варьировались. Также ученые подчеркивают, что не смогли бы отличить логарифмически преобразованное среднее положение xCG или zCG от ожидаемого, если бы птицы были просто масштабированы с сохранением всех шкал длины (2f).
Незначительный эффект, вызванный локтем и запястьем, наталкивает на вопрос, не отразится ли это также и на движении плечевого сустава. Для получения консервативной оценки было выдвинуто предположение, что крылья могут вращаться вокруг головки плечевой кости на 90° вперед, назад, вверх и вниз (прозрачные квадраты на 2b). Это показало, что максимальные сдвиги ΔxCG и ΔzCG составляли 18% (10.9 см) для большой голубой цапли, что примерно в шесть раз больше, чем при изменении только локтя и запястья. Таким большим смещением центра тяжести нельзя пренебречь при составлении уравнений движения. Но у других видов птиц ситуация была кардинально иная. К примеру, у Chrysolophus amherstiae (алмазный фазан) смещение при движении плечевого сустава было незначительное (1%, т.е. 1.4 см).
Тем не менее во всем диапазоне таксонов была обнаружена значительная положительная связь между xCG из-за движения плеча и отношением максимального размаха крыльев к длине тела (2d). Эта тенденция предполагает, что правильное моделирование динамики полета для птиц с крыльями, значительно превышающими длину их тела, потребует оценки ожидаемого смещения центра тяжести, чтобы проверить, является ли фиксированный центр тяжести правильным предположением.
Хоть центр тяжести всей птицы целиком и определяет ее симметричную динамику полета, параметры только крыльев могут дать представление об асимметричных конфигурациях. Было обнаружено, что ROM локтя и запястья вызывает смещение центра тяжести крыла вдоль оси yCGwing от 10% у Cypseloides niger (черный американский стриж) до 27% у Pelecanus erythrorhynchos (американский белый пеликан) и 28% у Aechmophorus occidentalis (западноамериканская поганка) (2c).
Смещение центра тяжести в значительной степени было вызвано разгибанием локтя (P <0.001, частичный η2 > 0.51; 2e), тогда как влияние запястья различалось у разных видов. В отличие от предыдущего исследования, в данном труде не было обнаружено, что логарифмически преобразованное среднее yCGwing отличается от изометрических ожиданий (2g).
Стоит отметить, что центр тяжести играет решающее значение в формировании основных уравнений, описывающих маневренность птиц, но вот решение этих уравнений зависит еще и от ротационной инерции.

Изображение №3
Было установлено, что инерция вращения птицы, как и центр тяжести, изометрически масштабируется с массой тела (3a). Однако разгибание локтя запястья обеспечивает более чем 11-кратное увеличение Ixx (большая голубая цапля) и 3-кратное увеличение Izz (цапля и сипуха) (3c). Эта способность была в значительной степени обусловлена разгибанием локтя (3b), что оказало значительное влияние как на Ixx (частичный η2 > 0.23) и Izz (частичный η2 > 0.45). На абсолютные значения Iyy и Ixz минимально влияло разгибание сустава, а величина эффекта существенно различалась у разных видов (3b).
Далее был рассчитан вклад каждой основной части тела в общую инерцию вращения для птиц с крыльями, максимально разогнутыми в локтях и запястьях (3d—3f). Поскольку крылья были вытянуты вдоль оси y, это отражает приблизительно наименьший их вклад в Iyy, но наибольший в Ixx. Процентный вклад каждой части тела существенно различался у разных видов, но, как и ожидалось, крылья отвечали за большую часть этого вклада по отношению к Ixx. Эти результаты показывают, что ROM локтя и запястья обеспечивает значительный инерционный контроль по осям крена и рыскания (Ixx, Izz), но в меньшей степени по оси тангажа (Iyy).
Затем ученые проверили, можно ли использовать инерционные характеристики для оценки маневренности птицы.
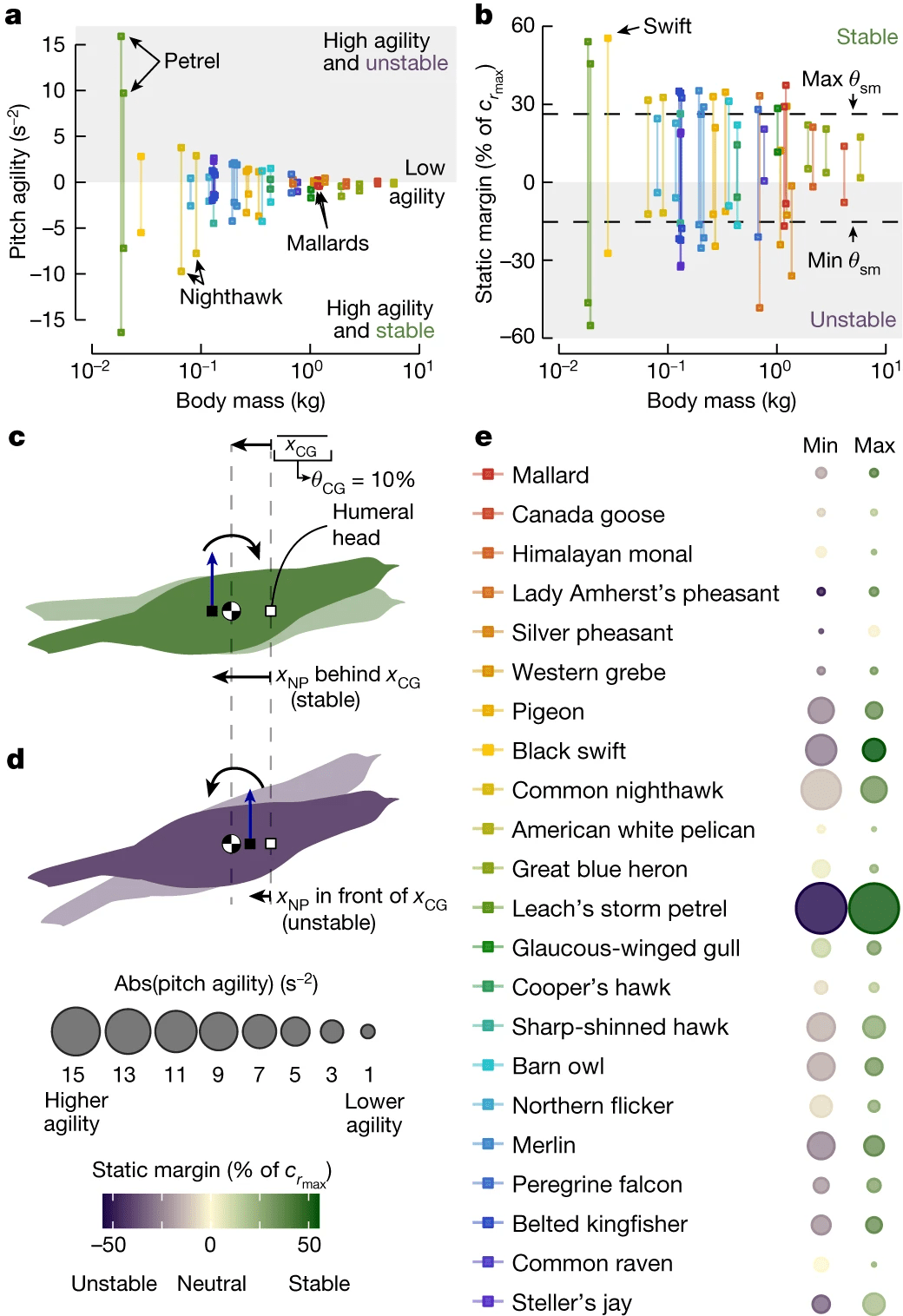
Изображение №4
В первую очередь была использована модель аэродинамики жесткого крыла чайки, чтобы получить оценку нейтральной точки и, следовательно, статический запас для каждой конфигурации. Вызвано это решение тем, что и инерция, и аэродинамика являются основополагающими для динамики полета. В результате была получена основная метрика маневренности по тангажу, которая пропорциональна угловому ускорению вокруг оси y из-за изменения угла направления полета.
Анализ показал, что диапазон маневренности по тангажу уменьшается по мере увеличения массы тела, что и ожидалось, поскольку скорость полета и размер тела положительно зависят от массы (4a). Эти результаты дополнительно обусловлены статическим запасом, диапазон которого также уменьшается по мере увеличения массы (4b).
Для ученых было важно не только понять основные принципы маневренности летающих птиц, но и выяснить эволюционные корни этой способности. Для этого они использовали статический запас, потому что он одновременно является компонентом показателя маневренности по тангажу и определяет статическую устойчивость летящей птицы.
В результате были определены конфигурации с максимальным и минимальным статическим запасом для каждой особи. Затем было рассчитано среднее значение каждого признака для каждого вида (4b).
Это позволило установить, что 4 вида были полностью «стабильны», один вид был полностью «нестабилен», а 17 видов обладали способностью переключаться между стабильным и нестабильным полетом (4b и 4e).
Ранее предполагалось, что современные птицы склонны к стабильному полету. Результаты исследования говорят о том, что эволюционное давление может сохранять способность переключаться между стабильными и нестабильными конфигурациями. Сгибание и разгибание локтя и запястья сами по себе дают птицам возможность переключаться между этими режимами. Однако пока неизвестно, когда и при каких обстоятельствах птица будет это делать.
Суть в том, что динамическое переключение между стабильным и нестабильным режимами, вероятно, требует существенно разных алгоритмов управления, и, таким образом, переключение между этими режимами потребует сложной системы управления полетом. Сохраняя способность перемещать нейтральную точку крыла и корпуса перед центром тяжести, птицы могут достичь равновесного, хотя и нестабильного, состояния полета.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
В рассмотренном нами сегодня труде ученые уделили внимание полету птиц, которые в зависимости от условий демонстрируют два режима полета: стабильный (планирование) и нестабильный (маневрирование). Особое внимание было уделено крыльям, а также способности птиц менять их конфигурацию, т.е. трансформировать путем изменения положения той или иной части крыла.
Результаты труда показывают, что ROM (диапазон движения) локтя и запястья имеют небольшое влияние на положение центра тяжести и инерцию по тангажу, но оказывают существенное влияние на инерцию крена и рыскания.
Птиц, конечно, много, и ученые понимают, что существует множество отличий как между видами, так и между особями одного вида. Однако одного только ROM запястья и локтя достаточен для переключения между стабильным и нестабильным полетом у 17 из 22 исследованных видов птиц.
Кроме того, эволюционный анализ показывает, что фенотипический оптимальный максимальный и минимальный статический запас поддерживает способность к переходу между стабильным и нестабильным полетом, что указывает на необходимость сложной системы управления полетом.
Данный труд, по словам его авторов, является еще одним важным шагом для более полного понимания и количественного описания полета и маневренности летающих птиц. Что, в свою очередь, позволит применить полученные данные в авиастроении и разработке более эффективных беспилотных летательных аппаратов, которые смогут менять свою конфигурацию динамически в зависимости от условий окружающей среды.
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?





