[Перевод] Загадочные структуры объединяют математику и природу

В городе Куэрнавака в Мексике «шпионская» сеть повышает эффективность автобусного парка. В результате расписание отбытия автобусов везде соответствует шаблону «универсальности»

В 1999 году, сидя на автобусной остановке в городе Куэрнавака в Мексике, чешский физик Петр Шеба [Petr Šeba] заметил людей, дававших водителю автобуса кусочки бумаги в обмен на деньги. Он обнаружил, что это было не проявление организованной преступности, но другая «теневая» торговля: каждый водитель платил «шпиону», отмечавшему, когда предыдущий автобус отошёл от остановки. Если он отошёл недавно, то водитель этого автобуса замедлялся, чтобы на следующей остановке успели собраться пассажиры. Если тот автобус отошёл уже давно, водитель ускорялся, чтобы его не обогнали другие автобусы. Такая система максимизировала прибыль водителей. Что и дало Шебе идею.

«Мы подумали, что наблюдаем ситуацию, чем-то напоминающую хаотические квантовые системы», пояснил соавтор Шебы, Милан Крбалек [Milan Krbálek].

После нескольких неудачных попыток пообщаться со «шпионами», Шеба попросил своего студента объяснить тем, что он не был из налоговой или из мафии. Он – просто безумный учёный, меняющий текилу на их данные. И люди отдали ему свои записи. Когда исследователи построили графики тысяч времён отхода автобусов, их подозрения подтвердились. Взаимодействие между водителями приводило к распределению промежутков между отходами транспорта, совпадающему со структурой некоторых экспериментов по квантовой физике.

«Я думал о том, что нечто подобное может появиться, но я удивился, увидев такое точное совпадение»,- сказал Шеба.

У субатомных частиц мало общего с децентрализованной автобусной системой. Но за годы, прошедшие с открытия странных квантовых взаимодействий, те же структуры данных появлялись в других, не связанных с ними ситуациях. Учёные считают, что это распространённое явление, известное, как «универсальность», происходит из-за математической связи явлений, и помогает им моделировать сложные системы, от интернета до климата планеты.

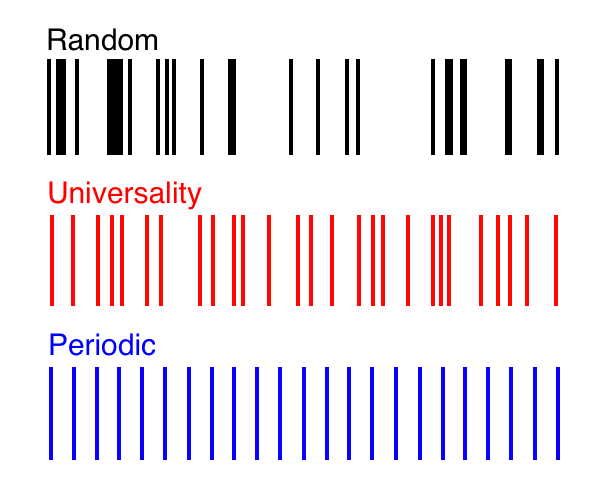
Красный график представляет собой идеальный баланс между случайностью и периодичностью, известный, как универсальность. Он наблюдается в спектрах многих сложных систем с корреляцией. В этом спектре математическая корреляционная функция даёт точную вероятность наличия двух линий на заданном расстоянии друг от друга

Такая структура впервые нашлась в природе в 1950-х годах в энергетическом спектре уранового ядра, монстра с сотнями движущихся частей, колеблющихся и растягивающихся бесконечным числом способов, и выдающих бесконечную последовательность уровней энергии. В 1972 специалист по теории чисел Хью Монтгомери наблюдал её в нулях дзета-функции Римана, математического объекта, связанного с распределением простых чисел. В 2000 Крбалек и Шеба обнаружили её в графике отхода автобусов в Куэрнаваке. А недавно она появилась в спектральных измерениях композитных материалов, таких, как морской лёд и человеческая костная ткань, и в динамике сигналов модели Эрдёша-Реньи, упрощённой версии интернета.

У каждой из этих систем есть спектр – последовательность-штрихкод, представляющая такие данные, как уровни энергии, нули дзеты, время отхода автобусов или скорость сигналов. Одинаковые структуры появляются во всём спектре. Распределение данных выглядит случайным, но при этом соседние линии «отталкиваются» друг от друга, что приводит к определённой регулярности промежутков. Точный баланс между хаосом и порядком, определяемый формулой, также появляется в чисто математических задачах: он определяет расстояние между собственными значениями матрицы, заполненной случайными числами.

«Почему так много физических систем ведут себя наподобие случайных матриц, остаётся загадкой»,- говорит Хорнг Тзер Яо, математик из Гарвардского университета. «Но за последние три года мы совершили очень важный шаг для понимания этого».

Для исследования феномена универсальности в случайных матрицах учёные немного разобрались в том, почему он появляется везде, и как его можно использовать. В ворохе новых работ Яо и другие математики описали много новых типов случайных матриц, подчиняющихся нескольким числовым распределениям и правилам симметрии. К примеру, числа для столбцов и строк матриц можно брать с кривой нормального распределения возможных значений, или можно заполнить её значениями 1 и -1. Верхняя правая и нижняя левая части матрицы могут зеркально отображать друг друга, а могут и не отображать. И вне зависимости от их характеристик, случайные матрицы демонстрируют те же самые хаотичные, но регулярные спектры в распределении их собственных значений. Поэтому математики и назвали это явление «универсальностью».

«Выглядит, как закон природы»,- говорит Ван Ву, математик из Йельского университета, доказавший вместе с Теренсом Тао из Калифорнийского университета в Лос-Анджелесе универсальность для широкого класса случайных матриц.

Считается, что универсальность появляется в очень сложных системах, состоящих из многих частей, тесно взаимодействующих друг с другом для создания спектра. Конфигурация появляется в спектре случайной матрицы, например, оттого, что все элементы матрицы используются при вычислении этого спектра. Но случайные матрицы, по словам Ву – это просто «игрушечные системы», они достаточно простые для изучения, и достаточно богатые для моделирования реальных систем. Универсальность распространена гораздо больше. Гипотеза Вигнера (названная в честь Юджина Вигнера, фиизка, открывшего универсальность в спектре атомов), предполагает, что все сложные системы с корреляцией обладают универсальностью, от кристаллической решётки до интернета.

Чем сложнее система, тем сильнее в ней проявляется универсальность, говорит Ласло Эрдёш из Мюнхенского университета, один из коллег Яо по работе. «Вы верим, что универсальность – это типичное поведение».

Во многих простых системах отдельные компоненты могут слишком сильно влиять на общий результат работы, что меняет вид спектра. У более крупных систем нет доминирования ни одного отдельного компонента. «Получается, будто есть комната с большим количеством людей, решающих что-то сделать, и личность одного из них не так важна»,- говорит Ву.

Математики используют случайные матрицы для изучения и предсказания некоторых свойств интернета, например, размера типичного компьютерного кластера

Когда система демонстрирует универсальность, это служит гарантией того, что она сложная и внутри неё есть достаточно корреляции для того, чтобы её можно было интерпретировать как случайную матрицу. «Это значит, что для её моделирования можно использовать случайную матрицу»,- говорит Ву. «Вы можете подсчитывать другие параметры модели на основе матрицы и использовать их для предсказания поведения этой системы».

Эта техника позволяет учёным понимать структуру и эволюцию интернета. Некоторые свойства этой огромной компьютерной сети, такие, как типичный размер кластера компьютеров, можно довольно точно оценить через измеряемые свойства соответствующей случайной матрицы. «Люди интересуются кластерами и их расположением, и это часто обусловлено практическими целями, такими, например, как реклама», говорит Ву.

Схожие технологии могут привести к улучшениям моделей изменений климата. Учёные обнаружили, что наличие универсальности, схожих с энергетическим спектром, в материале, говорит о сильной связанности его частей, и, как следствие, о хорошей проводимости жидкостей, электричества или тепла. И обратно, отсутствие универсальности может говорить о разреженности материала и его изолирующих свойствах. В новой работе, представленной на математической конференции в Сан-Диего, Кен Голден, математик из Университета Юты, и его студент, Бен Мёрфи, использовали это различие для предсказания показателей проводимости тепла и потоков жидкостей в морском льде, как на микроскопическом уровне, так и у арктических полыней, присутствующих на территориях, простирающихся на тысячи километров.

Спектральное измерение мозаики растаявших полыней, сфотографированной с вертолёта, или данные по морскому льду, полученные из пробы, показывают состояние каждой из этих систем. «Поток жидкости через морской лёд управляет очень важными процессами, которые необходимо понять, чтобы разобраться в работе климатической системы,- говорит Голден. – Переходы в статистике собственных решений представляют новый, математически строгий подход к включению морского льда в климатические модели».

Тот же трюк может привести к созданию простого теста на остеопороз. Голден, Мёрфи и их коллеги обнаружили, что спектр плотной, здоровой кости, обладает универсальностью, в то время, как спектр пористой – нет.

Арктические полыньи отличаются универсальностью в случае наличия у них достаточной связанности

«Мы работаем с системами, „частицы“ которых могут быть миллиметрового или километрового размера,- говорит Мёрфи про компоненты систем. – Удивительно, что одна и та же математика описывает их все».

Причина, по которой реальные системы обладают схожим со случайной матрицей поведением, возможно, проще всего понять в случае ядра тяжёлого атома. Все квантовые системы, включая атомы, работают по правилам математики, особенно с участием матриц. «Это суть квантовой механики,- говорит Фриман Дайсон, в прошлом физик-математик, помогавший разрабатывать теорию случайных матриц в 1960-х и 1970-х в Принстонском институте перспективных разработок. – Каждая квантовая система описывается матрицей, представляющей её общую энергию, и собственные решения матрицы – это энергетические уровни квантовой системы».

Матрицы простых атомов, водорода и гелия, могут быть подсчитаны точно, и полученные собственные решения с удивительной точностью совпадают с измеренными энергетическими уровнями атомов. Но матрицы более сложных систем, таких, как ядро урана, становятся слишком «колючими», чтобы «ухватить» их. По Дайсону, из-за этого такие ядра и можно сравнить со случайной матрицей. Многие взаимодействия внутри урана – элементы неизвестной матрицы – настолько сложны, что их смесь даёт шум, как множество наложенных звуков. В результате, неизвестная матрица, управляющая ядром, ведёт себя, как матрица со случайными числами, и их спектр обладает универсальностью.

У таких, не связанных между собой полыней, нет универсальности, их спектр случаен

Учёные ещё не выработали интуитивного понимания того, почему сложные системы демонстрируют именно эту, а не другую случайно/периодическую последовательность. «Нам это известно только из расчётов»,- говорит Ву. Другая загадка – их связь с дзета-функцией Римана, у которой универсальность проявляется в спектре нулей. Эти нули тесно связаны с распределением простых чисел – несокращаемых целых чисел, из которых состоят все остальные. Математики давно ищут описание распределения простых чисел по числовой прямой от 1 до бесконечности, и универсальность даёт им ключ. Некоторые считают, что за дзета-функцией Римана может стоять матрица, достаточно сложная и связная для обладания универсальностью. Открытие такой матрицы оказало бы «сильное влияние» на понимание распределения простых чисел, как сказал Пол Бургад [Paul Bourgade], математик из Гарварда.

Возможно, что объяснение скрыто ещё глубже. «Может оказаться, что в центре универсальности Вигнера и дзета-функции лежит не матрица, а некая пока ещё не открытая математическая структура,- говорит Эрдёш. – Матрицы Вигнера и дзета-функции могут оказаться разными представлениями этой структуры».

Многие математики ищут ответ без гарантии наличия такового. «Никто не представлял, что автобусы в Куэрнаваке станут таким примером. Никто не представлял, что нули дзета-функции будут другим примером,- говорит Дайсон. – Прелесть науки в её непредсказуемости, и поэтому всё полезное появляется из сюрпризов».