«Это легко. Берём метрику Шварцшильда, ищем символы Кристоффеля, вычисляем их производную, записываем геодезическое уравнение, меняем некоторые декартовы координаты (чтобы не страдать), получаем большое многострочное ОДУ — и решаем его. Примерно так».

Теперь ясно, что чёрные дыры меня засосали. Они бесконечно увлекательны. В прошлый раз я разбирался с визуализацией геометрии Шварцшильда. Меня поглотила проблема точного представления, как кривизна такого пространства-времени влияет на внешний вид неба (поскольку фотоны из удалённых источников движутся вдоль геодезических линий, изогнутых чёрной дырой) для создания интерактивного моделирования. Вот результат (работает в браузере). Хитрость в максимально возможном предрасчёте отклонения световых лучей. Всё работает более-менее нормально, но конечно, такая симуляция далека от идеала, потому что в реальности там не производится никакой трассировки (для неспециалистов: восстановление назад во времени местонахождения световых лучей, падающих в камеру).

Мой новый проект исправляет этот недостаток, отказавшись от эффективности/интерактивности самым простым образом: это рейтрейсер чисто на CPU. Трассировка выполняется максимально точно и максимально долго. Рендеринг изображения вверху занял 15 5 минут (спасибо, RK4) на моём ноутбуке.

Здесь нет какого-то улучшения по сравнению с аналогичными работами. Просто мне действительно нравится этим заниматься. Я пишу эту статью, чтобы поделиться не только результатами, как изображение выше (тем более, что у других получилось лучше), но и процессом создания этих изображений, с обсуждением/объяснением физики и реализации. В идеале, это может вдохновить или стать руководством для людей с похожими интересами.

Свежие рендеры ищите по тегу starless на tumlr.

Немного псевдо-римановой оптики

Тень

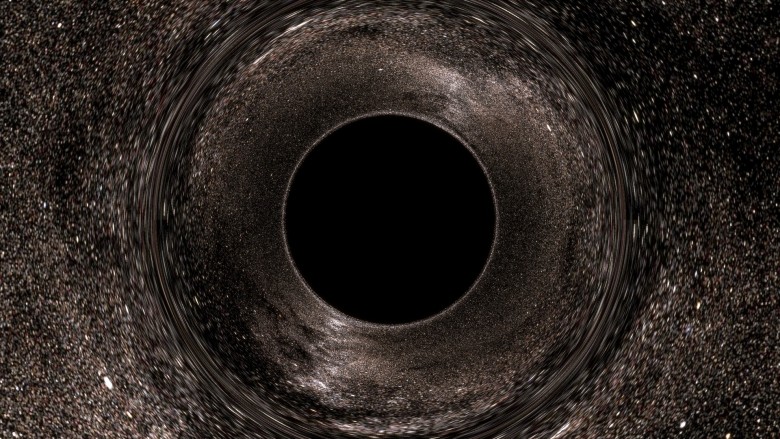
Если вы уже опробовали мой апплет, то знакомы с такой картинкой:

На ней хорошо выделяются главные особенности: чёрный диск и странное кольцо искажений.

В дискуссиях часто обращают внимание: неправильно говорить, что чёрный диск — это горизонт событий. На самом деле неправильно говорить, что область изображения является объектом. Это изображение объекта. Действительно, есть траектории, которые при отслеживании от вашего глаза до источника окажутся в горизонте событий (ГС). Это чёрные пиксели, поскольку ни один фотон не может пройти по этой траектории от чёрной дыры (ЧД) до вашего глаза. Таким образом, этот чёрный диск очень чётко представляет собой изображение горизонта событий, в том смысле, что если вы нарисуете (в далёком прошлом) что-то прямо над горизонтом, то внешние наблюдатели смогут увидеть его прямо на этом чёрном диске (мы фактически выполним этот эксперимент позже). В некоторых публикациях этот чёрный регион также называют «тенью» ЧД.

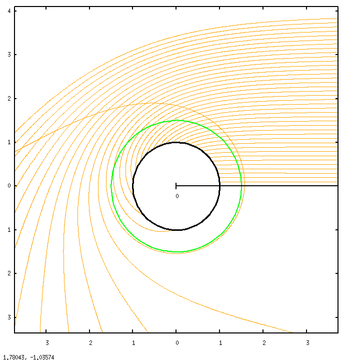
Однако интересно отметить, что это одновременно и изображение фотонной сферы (ФС). График gnuplot вверху изображает геодезию входящих фотонов из бесконечности (глядя на ЧД издалека при зуммировании) вместе с ГС (чёрный) и ФС (зелёный). Радиус фотонной сферы в 1,5 раза больше, чем радиус горизонта событий (в геометрии Шварцшильда) и здесь разрешены круговые орбиты фотонов вокруг ЧД (хотя и неустойчивые). На графике некоторые лучи падают в небытие, а другие рассеиваются (и, таким образом, оказываются на другой точке небесной сферы). Видно, что у поглощаемых лучей параметр воздействия менее ~2,5 радиусов. Это очевидный радиус чёрного диска, и он значительно больше, чем ГС и ФС.

В любом случае, важен такой факт:

Световой луч, свободно падающий в фотонную сферу, также достигнет горизонта событий.

Это означает, что изображение фотонной сферы включено в изображение горизонта событий. Но поскольку ГС явно находится внутри ФС, изображение первого также должно быть подмножеством последнего. Тогда два изображения должны совпадать.

Почему мы проверяем, что чёрный диск также является изображением ФС? Потому что это означает, что край чёрного диска заполнен фотонами, которые скользят по фотонной сфере. Пиксель сразу за пределами чёрного диска соответствует фотону, который (при трассировке обратно) спирально падает в фотонную сферу, всё ближе и ближе к неустойчивой круговой орбите, закручиваясь много раз (чем ближе вы смотрите, тем быстрее он закручивается), а затем по спирали выскакивает — поскольку орбита неустойчива — и убегает в бесконечность.

Такое поведение вызовет интересный оптический эффект, похожий на сепаратрису в динамической системе. Теоретически, если луч запущен точно по краю, он будет вечно закручиваться в спираль, всё ближе и ближе к круговой орбите фотонной сферы.

Влияние на небесную сферу

Не будем заостряться на этой теме, потому что ей посвящён прошлый апплет, и он даёт гораздо лучшее представление об искажениях на небе (включая опцию UV grid для более чётких искажений).

Только пару слов о кольце Эйнштейна. Гравитационная линза оптически различима, потому что представляет собой изображение единственной точки, которая находится прямо напротив наблюдателя. Кольцо образуется при таком угле обзора, когда лучи от наблюдателя искривляются параллельно. Наружные лучи искривляются недостаточно сильно и остаются расходящимися; внутри же искривляются слишком сильно, сходятся и в реальности могут даже пойти назад или по кругу, как мы видели.

Но подумайте вот о чём: если подойти достаточно близко к чёрному диску, световые лучи могут сделать один круг, а затем уйти параллельно. Там мы должны увидеть вторичное кольцо Эйнштейна. По сути, могут быть кольца любого порядка (любое количество обмоток). Также между ними должны быть «нечётные» кольца, где лучи света изгибаются параллельно, но направлены в сторону зрителя. Эта бесконечная серия колец существует, но она абсолютно невидима на нашем изображении (на самом деле, на большинстве таких изображений), поскольку находится слишком близко к краю диска.

Искажение горизонта событий

На этой новой картинке кое-что изменилось. Прежде всего, она сделана в лучшем разрешении и с фильтрацией фона, чтобы сделать его более различимым. Затем я зуммировал изображение на ЧД (не приближаясь, мы по-прежнему находимся на расстоянии ~10 радиусов от неё, просто зум). Но самое главное, я нарисовал сетку на горизонте.

Горизонт — это «просто сфера». Технически, он не является стандартной римановой сферой с пространственной метрикой. Горизонт светоподобный! Это красочный способ сказать, что он распространяется со скоростью света. Однако в координатах Шварцшильда это всё ещё поверхность $\$inline\$r=1\$inline\$$, и мы можем использовать $\$inline\$phi\$inline\$$ и $\$inline\$theta\$inline\$$ как долготу и широту. Таким образом, можно каноническим способом нанести координатную сетку. Вы видите её на изображении.

Сетка позволяет увидеть особый эффект, который можно вывести, если проанализировать график рассеяния/поглощения фотонов выше:

Вся поверхность горизонта видна одновременно из любой точки.

Это очень интересно. Когда вы смотрите на неподвижную сферу в стандартном плоском пространстве-времени, то видите не более 50% её поверхности в любой момент времени (если приблизиться, то меньше 50% из-за перспективы). А вот горизонт виден полностью одновременно как чёрный диск: обратите внимание, в частности, на Северный и Южный полюсы. Тем не менее, хотя вся поверхность помещается на чёрный диск, она не покрывает его целиком: если зуммировать на край, вы увидите, что изображение ГС заканчивается до конца тени. Вы найдёте кольцо, расположенное очень близко к внешнему краю, но не до конца. Это изображение точки напротив наблюдателя и оно определяет границы этого «первого» изображения ГС внутри. Так что же находится между этим кольцом и фактическим краем? Я ещё не сгенерировал зуммированную картинку, но там ещё одно целое изображение горизонта событий. А потом ещё одно, и ещё одно, до бесконечности. Там бесконечные концентрические изображения всего горизонта, сжатого в тени. (Большое спасибо /u/xXxDeAThANgEL99xXx за указание на этот феномен, которой я пропустил).

Добавление аккреционного диска

Какой же современный рендеринг ЧД обойдётся без аккреционного диска? Хотя это явно спорный вопрос, действительно ли «Интерстеллар» Нолана доступен для наблюдения, не говоря уже о точности, но мы точно должны поблагодарить блокбастер за популяризацию конкретного искажения аккреционного диска. Здесь у нас бесконечно тонкий, плоский, горизонтальный аккреционный диск, простирающийся от фотонной сферы (хотя это очень нереалистично, потому что орбиты ниже $\$inline\$3r\_S\$inline\$$ неустойчивы, о чём говорится ниже) до 4 радиусов, раскрашенный в бело-синюю клетку. С такой окраской очевидно, что мы столкнулись с ещё одним случаем, когда одновременно видно 100% поверхности объекта.

Для этого изображения я переместил наблюдателя чуть повыше, чтобы взглянуть на диск немного сверху. Вы видите изображения двух граней диска: верхней и нижней. Изображение изгибается дугой над тенью ЧД, потому что луч, направленный прямо над чёрной дырой, наклоняется вниз, чтобы встретиться с верхней поверхностью диска за дырой, напротив наблюдателя.

Это также объясняет само существование нижнего изображения: лучи, идущие под ЧД, искривляются к нижней поверхности диска, которая позади ЧД. Если присмотреться, изображение распространяется по всей тени, но в верхней части оно намного тоньше. Это соответствует световым лучам, которые идут выше ЧД, делают почти полный круг вокруг дыры и ударяются в нижнюю поверхность перед диском.

Конечно, легко сделать вывод, что существует бесконечный ряд изображений аккреционных дисков, которые очень быстро истончаются по мере приближения к краю. Изображение следующего порядка уже очень тонкое, едва видно в нижней части края.

GIF’ки по-прежнему актуальны

В этой судорожной анимации я включаю/выключаю отклонение света (формально Шварцшильд/Минковский), чтобы прояснить некоторые моменты, о которых мы говорили.

Эти две странные гифки созданы по просьбам читателей. В первой наблюдатель кружит вокруг чёрной дыры на расстоянии в 10 радиусов. Это не следует понимать как фактическую орбиту, поскольку в реальности нет аберрации при движении по орбите. Здесь серия стационарных снимков ЧД из нескольких точек, где наблюдатель перемещается с места на место между кадрами; это «адиабатическая» орбита, если хотите.

И стерео тоже ещё актуально

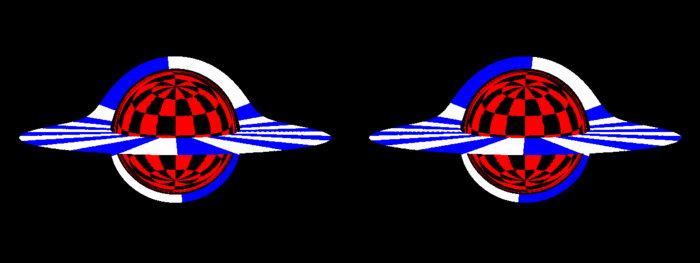
Интересно, что тень выглядит довольно плоской.

Хватит науки

Хватит с нас информативных картинок в стиле 90-х в низком разрешении с ядовитыми цветами. Вот несколько «попсовых» рендеров (нажмите для полного размера).

Это изображение сгенерировал пользователь /п/dfzxh с четырёхкратной избыточной выборкой

Более крупный план

Увеличенное изображение кольца

Культовый эффект «кольца света» при взгляде с экваториальной плоскости

Если скачать программу, то это текущая сцена по умолчанию

Гораздо более широкий диск

Ну да, ничего особенного. Здесь нет художественной работы, просто рендеры из программы. Давайте временно вернёмся к науке: третье изображение, которое как будто не имеет никакого смысла, на самом деле очень ценное. Это увеличенная область между верхним краем чёрного диска и основным изображением аккреционного диска. Наблюдатель находится на внешнем краю самого аккреционного диска и зуммирует картинку. Цель была в том, чтобы изобразить как можно больше колец разного порядка. Видны три порядка: более светлая зона в верхней части — это только нижний край первого изображения верхней дальней поверхности диска. Полоса внизу, под спокойным морем растянувшихся звёзд, является верхней частью изображения нижней передней части диска. В самом низу — тонкая линия света шириной не более пикселя, приклеенная к чёрному диску фотонной сферы. Это в основном третье изображение: снова верхняя дальняя поверхность, но после того, как свет завершил дополнительный оборот вокруг чёрной дыры. Слитые с ним, но всё более тонкие изображения — кольца более высокого порядка. Хорошо, это тоже достойно тега

:

Здесь бесконечные изображения и верхней, и нижней поверхности аккреционного диска, и все они показывают всю поверхность диска одновременно. Более того, кроме самого первого, эти изображения не проходят ни перед черным диском, ни друг перед другом, а потому являются «концентрическими».

Чудесно.

Принимаю запросы на рендеринг
Заинтересованы в конкретной визуализации, но не готовы пройти через трудности установки программы и рендеринга самостоятельно? Просто напишите мне Reddit или по почте. Рендеринг 1080p на моём ноутбуке занимает не более 10-20 минут.

Реалистичный аккреционный диск

Аккреционный диск в рендерах довольно мультяшный. Это просто диск с дурацкой текстурой. Что происходит, когда в визуальный облик диска включается реальная физика? Что происходит, если учесть красное смещение от орбитального движения, например?

Популярной моделью аккреционного диска является бесконечно тонкий диск вещества на почти круговой орбите. Он начинается с ISCO (самая внутренняя устойчивая круговая орбита, $\$inline\$3r\_s\$inline\$$) с температурным профилем по степенному закону $\$inline\$(T\; sim\; r^\{-a\}\$inline\$$. Я буду использовать очень простой вариант:

$\$\$display\$\$T\; sim\; r^\{-3/4\}\$\$display\$\$$

что определённо ненормально в общей теории относительности для реалистичных жидкостей, но здесь так (в любом случае, разницу вы не заметите).

Теперь свободным параметром является общая шкала для температур, например, температура в ISCO. Эта температура огромна для большинства чёрных дыр. Мы говорим о сотнях миллионов Кельвинов; трудно представить себе какой-либо человеческий артефакт, который сумел бы существовать, подвергаясь воздействию излучения диска (пик в рентгеновском излучении) на таких температурах, не говоря уже о фотосъёмке. Так что нам явно надо снизить температуру. Очевидно, сверхмассивные чёрные дыры холоднее, но недостаточно. Нужно снизиться до 10 000 К в ISCO, чтобы мы могли хоть что-то увидеть. Это очень неточно, но это всё, что я могу сделать.

Следует задать два вопроса. Первый: какого цвета чёрное тело при такой температуре? Второй: насколько оно яркое? Формально ответ на эти два вопроса находится в скалярном произведении функций, описывающих каналы R, G, B со спектром чёрного тела. На практике используются некоторые приближения.

Для цвета вполне точна и эффективна эта формула Таннера Хелланда, но она включает в себя многочисленные условия, которые невыполнимы с моей трассировкой лучей (подробнее см. ниже). Самый быстрый способ — использовать простую текстуру:

Эта текстура — одна из многих полезных штучек в подборке Митчелла Чарити «Какого цвета чёрное тело?». Для справки, оно соответствует точке белого Е (whitepoint E).

Шкала показывает цвет чёрного тела при температуре от 1000 K до 30 000 K, более высоким температурам соответствует примерно такой же оттенок синего. Поскольку между температурами существует огромная разница в яркости, эта текстура не может передать и не передаёт яркость; скорее, она нормализует цвета. Наша задача — вычислить относительную яркость и применить её. Для этого подходит аналитическая формула. Если предположить, что видимый спектр очень узкий, то общая видимая интенсивность пропорциональна спектру самого чёрного тела:

$\$\$display\$\$frac\{1\}\{lambda^5\}\; frac\{1\}\{\; exp(\; frac\{hc\}\{lambda\; k\_B\; T\})\; —\; 1\; \}\$\$display\$\$$

где я избавился от глупых общих констант (мы всё равно собираемся масштабировать яркость, чтобы что-то увидеть). Можно просто вставить $\$inline\$lambda\$inline\$$ примерно для видимого диапазона спектра, и мы получим, что яркость пропорциональна температуре по такой формуле:

$\$\$display\$\$(\; e^\; \{\; frac\{29622.4\; text\{K\}\}\{T\}\; \}\; —\; 1\; )^\{-1\}\$\$display\$\$$

Это достаточно просто. В качестве проверки отметим, что относительная интенсивность быстро падает до нуля при приближении T к нулю, и практически не изменяется, когда T уходит в бесконечность.

Красное смещение

Мы обсуждали орбитальные скорости в геометрии Шварцшильда в описании апплета. Для вычисления красного смещения используется формула красного смещения из СТО:

$\$\$display\$\$(1+z)\_text\{Doppler\}\; =\; frac\{\; 1\; —\; beta\; cos(theta)\; \}\; \{sqrt\{1-beta^2\}\; \}\$\$display\$\$$

Где as $\$inline\$cos(theta)\$inline\$$ — косинус угла между направлением луча, испускаемого диском, и локальной скоростью диска, вычисленный в локальной инерциальной системе координат Шварцшильда. Формула верна в данном контексте благодаря принципу эквивалентности.

Её необходимо умножить на коэффициент гравитационного красного смещения:

$\$\$display\$\$(1+z)\_text\{Gravitational\}\; =\; (1\; —\; r^\{-1\})^\{-1/2\}\$\$display\$\$$

этот коэффицент не зависит от траектории светового луча, а только от радиуса излучения, поскольку геометрия Шварцшильда является стационарной.

Это также означает, что вклад позиции наблюдателя в гравитационное красное смещение постоянен по всему полю зрения. Всё наше изображение имеет постоянное общее синее смещение, потому что мы находимся глубоко в ЧД. Поэтому данный эффект даёт только слабый оттенок, который можно игнорировать.

Мы также пренебрегаем красным смещением от движения наблюдателя, потому что наш наблюдатель стационарен в геометрии Шварцшильда. Вот итоговый результат:

Как видите, бóльшая часть диска полностью белая из-за максимальной яркости в цветовых каналах. Если опустить эти каналов до диапазона 0,0−1,0, то внешние части диска станут бледными или чёрными. Рост яркости слишком велик, чтобы его увидеть и оценить. Я попытался проявить эффект с помощью постобработки, чтобы самые яркие части показали переход цветов, но этого вряд ли достаточно.

Довольно запутанная картина. Вот изображение без учёта яркости, где можно оценить цвета:

У этих картинок меньшее разрешение, потому что они очень долго рендерятся на моём ноутбуке (квадратные корни — это плохо, дети).

В любом случае, этот рендер в тысячу раз менее зрелищный, чем другие (в основном, потому что внутренний край диска уже достаточно далеко от ГС, так что что линзирование слишком велико), но рендер хотя бы точен. Если вы найдёте чёрную дыру с температурой 10 000 K и хорошие солнцезащитные очки, то увидите именно это.

Ещё один снимок с близкого расстояния. Я неестественно поднял насыщенность для красоты:

Пишем рейтрейсер чёрной дыры

Исходник на Github

Есть очень большая и очевидная разница между оптикой чёрных дыр и численным интегратором, который выдаёт красивые обои для рабочего стола с разрешением 1080p. В прошлый раз я не публиковал свои рассуждения, а просто поднял большой и грязный репозиторий git. Сейчас хочу объяснить немного подробнее, а также постараюсь поддерживать код в более аккуратном виде и с комментариями.

Мой трассировщик не создавался хорошим, мощным, быстрым. В первую очередь я хотел, чтобы его было легко настраивать, чтобы он сам был простым, так что люди могли бы получить вдохновение и увидеть потенциал для улучшения: даже его несовершенство может подтолкнуть к тому, что кто-то решит написать собственный вариант. Вот краткий обзор алгоритмов и их реализации.

«Магический» потенциал

Итак, общая теория относительности, всё понятно. Это легко. Берём метрику Шварцшильда, ищем символы Кристоффеля, вычисляем их производную, записываем геодезическое уравнение, меняем некоторые декартовы координаты, чтобы избежать бесконечных страданий, получаем огромное многострочное ОДУ, решаем его. Примерно так.

Просто шучу. Конечно, есть одна хитрость.

Если помните, в прошлый раз я вывел следующее уравнение для орбиты безмассовой частицы в её орбитальной плоскости в геометрии Шварцшильда ($\$inline\$u=1/r\$inline\$$):

$\$\$display\$\$u»(phi)\; +\; u\; =\; frac\{3\}\{2\}\; u^3\$\$display\$\$$

Хитрость в том, чтобы увидеть здесь формулу Бине. Для обладающей массой ньютоновской частицы в ньютоновском потенциале поля центральных сил:

$\$\$display\$\$frac\{d^2\}\{dt^2\}\; vec\; x\; =\; frac\{1\}\{m\}\; F(r)\$\$display\$\$$

тогда частица, очевидно, будет двигаться в своей орбитальной плоскости и соответствует формуле Бине для $\$inline\$u(phi)\$inline\$$:

$\$\$display\$\$u»\; +\; u\; =\; —\; frac\{1\}\{m\; h^2\; u^2\}\; F(u)\$\$display\$\$$

Где $\$inline\$frac\{d\}\{dphi\}\$inline\$$ — простое число, $\$inline\$m\$inline\$$ — масса, а $\$inline\$h\$inline\$$ — угловой момент на единицу массы. Это уравнение для орбиты, а не уравнение движения. Оно ничего не говорит о $\$inline\$u(t)\$inline\$$ или $\$inline\$phi(t)\$inline\$$, только показывает отношение между $\$inline\$u\$inline\$$ и $\$inline\$phi\$inline\$$.

Давайте остановимся на минутку, чтобы обдумать, что мы на самом деле получили. Уравнение говорит, что если представить гипотетическую механическую систему из частицы под действием определённой центральной силы, то её траектория будет решением формулы Бине. Затем механическая система становится инструментом вычисления формулы.

Именно это я предлагаю здесь. Мы указали $\$inline\$m=1\$inline\$$ и взяли (нефизическую, какую угодно) простую систему из точечной частицы в этом конкретном силовом поле:

$\$\$display\$\$vec\; F(r)\; =\; —\; frac\{3\}\{2\}\; h^2\; frac\{hat\; r\}\{r^5\}\$\$display\$\$$

где $\$inline\$h\$inline\$$ — некоторая константа, а уже численно решить уравнение очень просто. Тогда решение $\$inline\$vec\; x\; (T)\$inline\$$, где $\$inline\$T\$inline\$$ — абстрактная временная координата для этой системы, на самом деле является параметризацией единственного решения для соответствующего уравнения Бине, которое в точности является геодезическим уравнением.

Поэтому мы решаем ньютоновское уравнение в декартовых координатах, что вообще самое простое (я решил использовать метод Рунге — Кутты, чтобы появилась возможность увеличить размер шага и уменьшить время рендеринга, но в будущем пользователь сможет выбрать иной метод решения). Тогда мы получаем просто фактическую светоподобную геодезию, где $\$inline\$T\$inline\$$ — параметр, идущий вдоль неё (в отличие и от шварцшильдовского $\$inline\$t\$inline\$$, и от нормального времени, которого не существует).

Это намного лучше предыдущего метода, который работал с полярными координатами в плоскости орбиты. Здесь вычисления производятся очень эффективно.

Трассировка лучей в numpy

Если посмотреть на исходники, вы увидите скрипт на Python. Ужас! Зачем писать трассировку лучей на Python? Все знают, как медленно выполняются циклы в Python, что всегда (почти) ставит крест на работе. Дело в том, что мы производим вычисления в numpy — и параллельно. Вот почему эта программа не сможет постепенно выводить на экране уже отрисованные части: она рендерит всё одновременно.

Первым делом создаём массив начальных условий. Например, массив (numPixel, 3) с векторами для всех пикселей изображения (numPixel — ширина изображения × высота изображения). Тогда вычисление каждого луча сводится к массивам типа (numPixel, ...). Поскольку операции с массивами в numpy выполняются очень быстро, и здесь всё статически типизировано (надеюсь, прямо сейчас я не говорю ничего глупого), то должно рассчитываться достаточно быстро. Может, это не C, но всё равно быстро. В то же время, у нас есть гибкость и ясность Python.

Этот метод ужасен для стандартной трассировки лучей, где у объектов диффузные, отражающие, преломляющие части и важно учитывать условия освещения. Например, выборочное отражение частей массива лучей — настоящий кошмар; отслеживание булевых значений или индексов циклов требует многочисленных масок, а циклы нельзя разбить. Но здесь другой случай: все объекты в нашей сцене только излучают свет: небо, раскалённый диск аккреции, чёрный как смоль горизонт событий и яркая пыль. На них не влияет падающий свет, и сам свет тоже спокойно проходит через них, разве что снизив интенсивность. Это приводит нас к алгоритму определения цвета:

Смешивание цветов

Это легко: просто нужно смешать все объекты между нами и источником луча с их соответствующими альфа-значениями, и разместить друг над другом, где самый дальний будет внизу. Инициализируем цветной буфер с альфа-прозрачным чёрным цветом, затем при пересечении с объектом обновляем буфер, смешивая цвет из объекта под нашим цветовым буфером. Такие же шаги выполняем для пыли (используем профиль плотности $\$inline\$r^\{-2\}\$inline\$$) и продолжаем итерации до конца. Обратите внимание, что альфа-канал работает и как Z-буфер, поскольку объект перестаёт вносить свой вклад после того, как луч пересёк непрозрачный объект (который таким образом установил альфа-значение буфера в 1,0).

Очевидный недостаток этого метода в том, что нельзя остановить трассировку луча после его расчёта, потому что он является частью массива, где продолжается трассировка других лучей. Например, после столкновения с горизонтом лучи продолжают беспорядочно блуждать после того, как попали в сингулярность — можете посмотреть, что происходит, если явно отключить объект горизонта. Алгоритм альфа-смешивания гарантирует, что они не повлияют на итоговое изображение, но эти лучи всё равно нагружают CPU.