Что такое музыка с точки зрения математики? Что такое «ля» или «ми»? То, как именно звуки образуются, хорошо понятно на гитаре.
Звук «ми» (свободное звучание 1-й струны), звук «ля» (1-я струна зажатая на 5 ладу). «Ми» — это 440 Гц. Что значит 440 Гц? Это 440 раз колеблется струна в секунду. Звук «ми» на 5 полутонов ниже, чем звук «ля» (зажатый на 5 ладу).

Еще на 7 полутонов ниже я получу снова «ми», т.е. октаву. Почему и свободное звучание первой струны и звучание струны, зажатой на 12 ладу, называется одинаковым словом «ми»?

Нам кажется, что играется одна и также нота. Дело в том, что длина струны этой точкой («ми» на 12 ладу) делится ровно пополам:
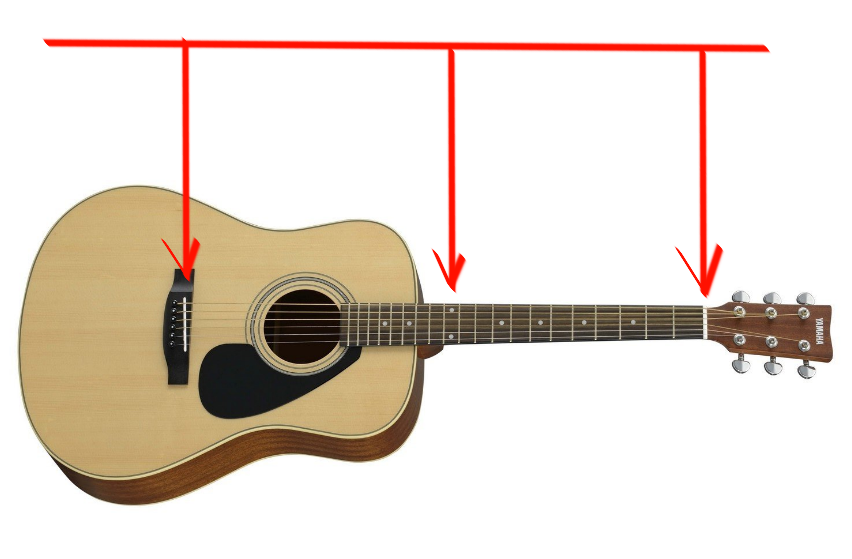
Это означает, что колебания этого остатка струны, по законам физики, будут в два раза более частые, чем колебания полной струны.
Каждый раз, когда я отступаю по струне, и зажимаю ее на следующем ладу (деление, обозначенное на грифе перпендикулярной чертой), звук поднимается на один полутон, как говорят музыканты.
Заметьте, что лады на грифе разной ширины. Они постепенно сужаются.Потому, что чтобы поднять частоту на один полутон, надо уменьшить длину струны в некоторое количество раз.
На что я намекаю, акцентируя внимание на том, что что-то «на» переводится во что-то «в»? Математики сказали бы, что есть единственная (в некоторых условиях) функция, где + переходит в х (умножить). И функция эта называется логарифм.
Это означает, что наши уши, укорачивание струны и поднятие звука в какое-то количество раз, воспринимают, как поднятие на один полутон. То есть каждый лад укорачивает струну в одно и тоже количество раз, а наши уши говорят, что мы поднимаемся на один полутон, доходя до ноты «ми» и получая октаву. Наши органы слуха устроены логарифмически.
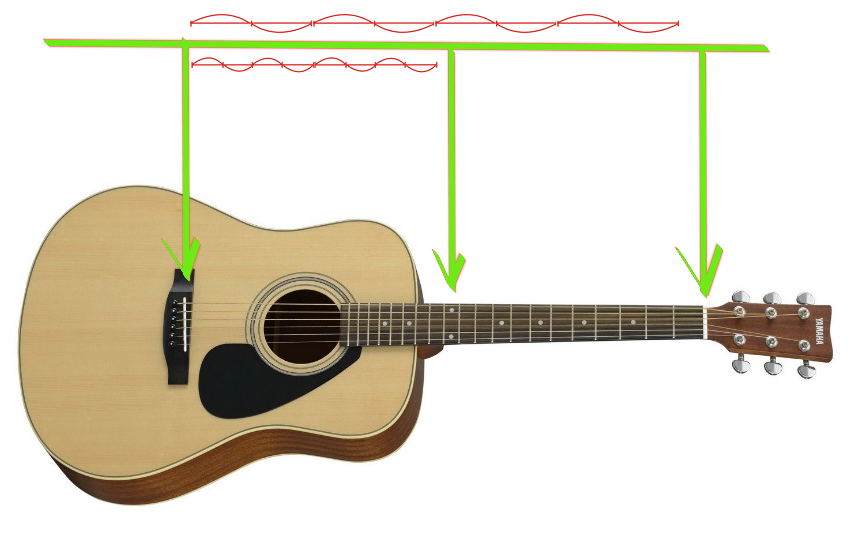
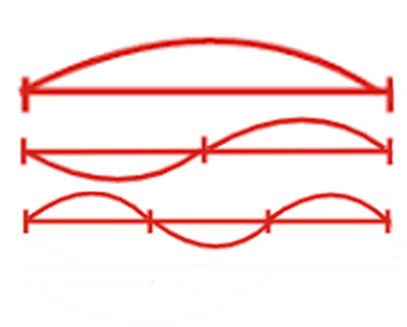
Мы говорим, что «ми» и «ми» отличаются в два раза, это видно по звучанию. Верхняя дуга — колебание полное. Когда мы зажимаем ее посередине, струна начинает колебаться, как на графике посередине.
Почему звуки похожи? Дело в том, что вместе с основным колебанием струны, на самом деле происходит колебание той же самой струны, во всех частотах, где длина колебательного участка обратно пропорциональная частоте.
Соответственно, если длина уменьшается в целое количество раз, то можно услышать соответствующую обертонику. Соответствующий обертон реализуем данной струной. Если данная струна колеблется частично зафиксировавшись в этих двух точках (нижний график), то ее тон будет в три раза более высокий.
Увеличение частоты в два раза воспринимается слухом, как та же самая нота. Все обертоны, которые мы делим в несколько раз, т.е. любое деление половинного отрезка, является и автоматическим делением и большого отрезка. И только некоторые деления большого отрезка не укладываются в схеме деления половинного.
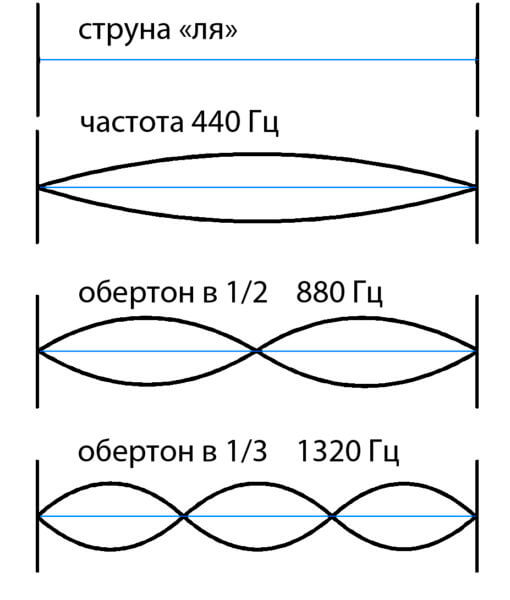
Если мы берем четные верхние звучания для длинной струны, то они будут верхними звучаниями и для струны, укороченной в два раза. И абсолютно любое укороченное звучание короткой струны, будет звучанием и для длинной. Потому мы и чувствуем, что все, что мы слышим совпадает в этих точках, и воспринимаем как одну ноту.
Еще интереснее, что есть ноты, идущие через несколько полутонов, и они воспринимаются ушами как созвучие, аккорд, что-то приятное для слуха, не режущее наш слух. Что это за ноты?
Если взять 7 полутонов, взять ноту «ля» и поднять звучание на 7 полутонов, до следующей «ми», то такие две ноты будут звучать хорошо.
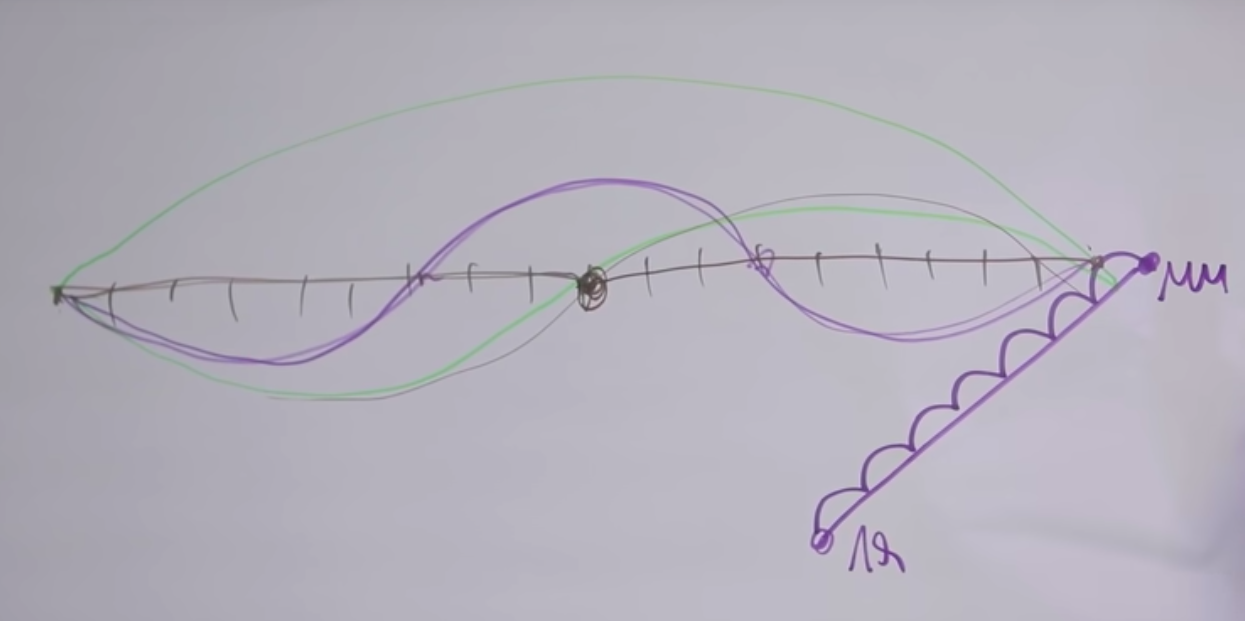
Если отступить еще на 5 полутонов вверх, то будет уже более высокая «ля» следующей октавы. Почему-то этот интервал тоже звучит для нас приятно. Давайте в этом всем разберемся.
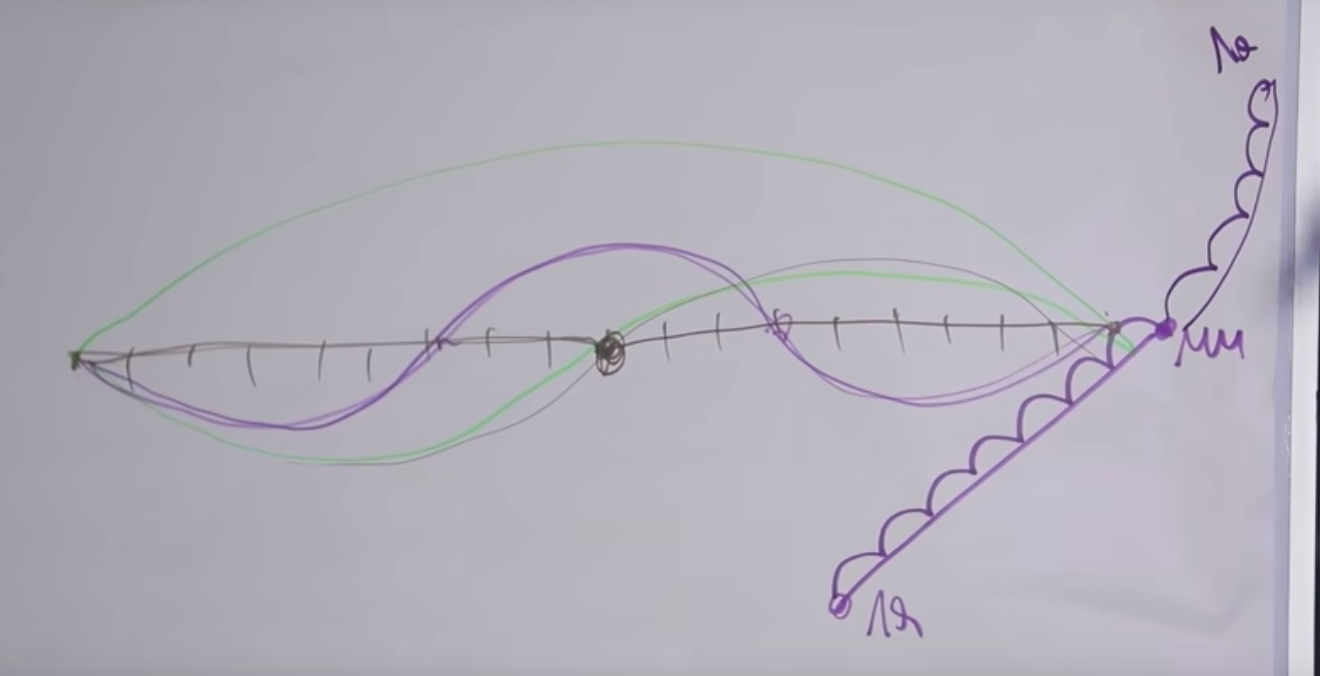
Прежде всего, если поднятие на 1 полутон, это увеличение частоты колебаний в какое-то количество раз, то обозначим его как х. Если нужно поднять еще на 1 полутон, то уже будет х*х, то есть x2. Если я поднял на 12 полутонов (x12), то это должно быть поднятием ровно в 2 раза. Мы получаем уравнение х12=2.
По этому увеличение на 1 полутон означает сокращение струны в х=12√2, или, что тоже самое, поднятие частоты звука, в 12√2.
А при чем тут «ля» и «ми»? Почему 7 полутонов звучит мелодично? Давайте возведем степень:
Что в этом числе такого приятного, хорошего?
Когда-то в древности изобрели темперированные клавиры, точную запись музыки. На гитаре это очень хорошо видно, у фортепиано это тоже можно найти, оно внутри прячется, если заглянуть, можно увидеть струны.
Так вот, это число — очень близко к числу 3/2. Если вычислять на калькуляторе, буде очень большая точность. Это значит, что «ми» приблизительно выше, чем предыдущая «ля» в 1,5 раза. Т.е. подъем на 7 тонов эквивалентен тому, что мы поднимаемся на 3/2 раза, из этого получается, что у нас очень много верхних обертонов совпадает.
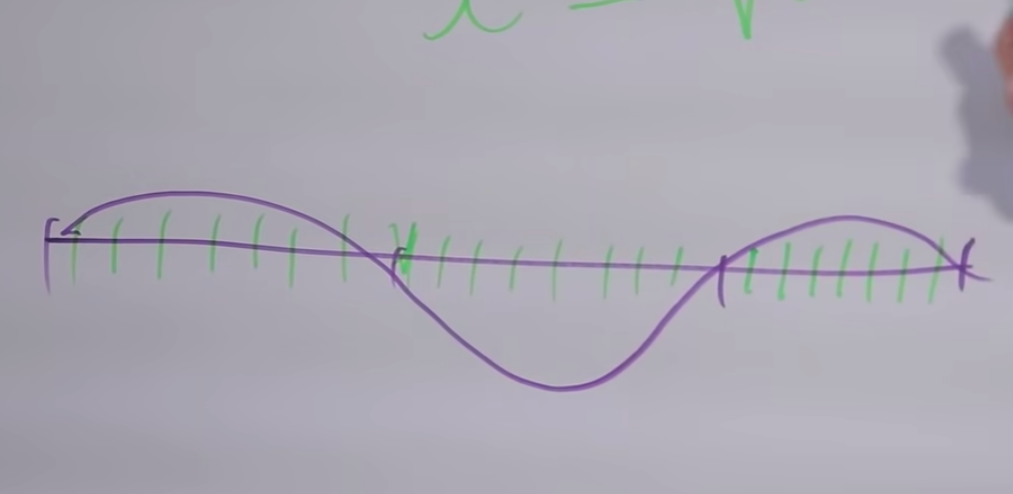
Потому что любое деление на целое число малого отрезка, будет делением на целое число всего отрезка. И, соответственно, деление исходного отреза на количество кусков, кратное трем, будет и делением малого отрезка (⅓), и ⅔ тоже. Когда мы оставили ⅔ от длины, т.е. подняли частоту в 3/2, это мы примерно поднялись на 7 полутонов, у нас будет много общих обертонов, это будет приятное созвучие.
Оставшиеся 4/3 — это как раз 5 оставшихся полутонов, 3/2 х 4/3 =2, как раз октава. Чему соответствует формула х71243. Значение очень близкое к 4/3, но не 100%, т.к. Это число является иррациональным, не записывается никакой дробью, его нельзя записать как целое число делить на целое число.
Я слушал, что в Индии есть инструмент (ситар), в котором на 19 частей делится октава, т.е. у них полутон = 1/19 октавы, 19х2.

И уже с огромной точностью х121932что означает, если на таком индийском инструменте отступить на 12 из 19 отрезков, то в этом созвучии будет больше совпадающих обертонов, и этом интервал звучит как бальзам на уши.
Про музыку и математику много чего интересного можно сказать. В частности, мажорным аккорд воспринимается, если к любой начальной ноте прибавить сначала 4 полутона, а потом 3, т.е. 0 — 4 — 3. А минорным, если в начале прибавлять 3, а потом 4, т.е. 0 — 3 — 4. Первая и последняя из трех нот аккорда, будет «одинаковая», она как раз отличается на 7 полутонов, а вот средний звук будет создавать наше восприятие созвучия, и настраивать на минорным или мажорный лад.
Казалось бы, музыка и математика, что может быть общего? А общего так много, что математики и музыканты часто общаются, более того математики легко понимают музыкантов, так сказать, схватывают с полутона.
Несколько полезных ссылок:


