Математика опционов или модель Блэка-Шоулза

13.04.2021

Всеобщий интерес к модели Блэка-Шоулза (далее — БШ) вызван тем, что в свое время ее авторы произвели революцию сфере оценки справедливой стоимости опционов и иных производных финансовых инструментов. В дальнейшем они получили Нобелевскую премию за свои открытия, а выведенная ими аналитическая формула, стала пожалуй, самой фундаментальной и известной в мире финансов.

Не меньший интерес модель БШ вызывает с точки зрения низкоуровневого математического и теоретико-вероятностного анализа. В статье подробно рассмотрен процесс обоснования опорных и ключевых принципов модели БШ, а также в процессе доказательств выводится аналитическая формула, которая используется для оценки справедливой стоимости опционов.

Базовые понятия

Опцион — договор, по которому покупатель опциона получает право, но не обязательство, совершить покупку или продажу данного актива по заранее оговорённой цене, которая называется ценой исполнения или страйк.

Для целей дальнейшего анализа такой финансовый инструмент наиболее точно представим в виде функции, которая описывает выплаты по опциону в момент экспирации контракта. Для более простого и интуитивного понимания, будем рассматривать опцион типа Call, функция выплат по которому выглядит следующим образом.

где, цена базового актива, цена страйк.

С практической точки зрения, функция предполагает получение выгоды покупателем опциона в случае, если цена базового активапревысит цену страйк x_s и которая будет совпадать с разностью [x-x_s] . В противном случае, держатель опциона получит убыток равный, уплаченной премии за приобретение опционного контракта.

Понятие справедливой стоимости наглядно иллюстрируется тем, что в момент заключения сделки ни одна из сторон не должна находится в преимущественном положении. Такая расстановка сил окажется возможной только в том случае, если стоимость опциона будет равна ожидаемой прибыли по нему. Иначе говоря, мы будем готовы заплатить за опцион ровно столько, сколько сможем на нем заработать (в среднем).

Исходя из вышесказанного, логичным становится исследование функции C= max(x - x_s; 0) , как случайного процесса, зависящего от цены базового активаи времени , поскольку данная функция будет определять получаемую по опциону прибыль в конкретный момент времени, а следовательно и его справедливую стоимость.

Уравнение БШ в частных производных

Чтобы продвинутся в направлении вывода формулы БШ необходимо обратиться к лемме Ито, позволяющей найти дифференциал функции, аргументом, которой является стохастический процесс. При этом необходимо знать стохастическое уравнение самого аргумента, являющегося случайным процессом.

Проанализируем применимость леммы Ито для нашего конкретного случая.

В самом деле, функция выплат C= max(x - x_s; 0) в качестве аргумента содержит случайный процесс x(t) . В силу того, что процесс x(t) является ценой базового актива, то наиболее логично допустить его описание дифференциальным уравнением логарифмического случайного блуждания: dx = xrdt + xsigma delta W *. В итоге получим две компоненты, требуемые для применения леммы Ито.

Подставив имеющиеся у нас данные в формулу Ито получим соотношение представленное ниже:

$dC = left(frac{partial C}{partial t} + xrfrac{partial C}{partial x} + frac{sigma^2}{2} frac{partial ^2 C}{partial x^2}right)dt + xsigmafrac{partial C}{partial x} delta W qquad (1)$

Нашему взору предстанет очень сложное дифференциальное стохастическое уравнение, которое имеет мало перспектив интегрирования в таком виде. Для упрощения уравнения (1) , требуется в первую очередь избавится от стохастической составляющей. Сделать это возможно путем формирования дельта-нейтрального портфеля.

$Pi = frac{partial C}{partial x} cdot x - C(x, t) qquad (2)$

где, $Delta = frac{partial C}{partial x}$ — дельта опциона или первая производная по .

Далее полагаем, что дельта опциона практически не меняется с изменением, таким образом Delta = const и дифференциальная форма дельта-нейтрального портфеля имеет следующий вид: d Pi = Delta cdot dx - dC . Заметим, чтонам известно, как логарифмическое случайное блуждание *, аберем из соотношения (1) . В итоге получаем:

$d Pi = Delta(xrdt + xsigma delta W) - left [ left(frac{partial C}{partial t} + xrfrac{partial C}{partial x} + frac{sigma^2}{2} frac{partial ^2 C}{partial x^2}right)dt + xsigmafrac{partial C}{partial x} delta W right ] qquad (3)$

Если не забыть, что $Delta = frac{partial C}{partial x}$ и раскрыть скобки, то стохастическая составляющая $xsigmafrac{partial C}{partial x} delta W$ сократится и останется:

$d Pi = - left [frac{partial C}{partial t} + frac{sigma^2}{2} frac{partial ^2 C}{partial x^2}right]dt qquad (4)$

Дифференциальное уравнение выглядит уже вполне пригодно, однако требуется провести еще несколько преобразований. Заменяем переменнуюна tau , как tau = T-t , где период. Обе переменные определяют срок до экспирации опциона, однако в случаенаш срок увеличивается, а после замены на tau , срок будет сокращаться. На уровне производных, осуществленная замена приведет к следующему тождеству: $frac{partial C}{partial t } = - frac{partial C}{partial tau }$ .

Опираясь на принципы B,S - рынка можно перейти к новому равенству: d Pi = Pi rdt , гдебезрисковая ставка. Левую часть этого равенства заменяем соотношением (4) , а вместов правой части уравнения подставляем формулу (2) .

$frac{partial C}{partial tau }dt - frac{sigma^2}{2} frac{partial ^2 C}{partial x^2}dt =left( frac{partial C}{partial x} cdot x - C(x, t) right ) rdt$

Раскроем скобки, разделим обе части наи получим уравнение БШ в частных производных:

$frac{partial C}{partial tau } + rC = frac{sigma^2 x^2}{2} frac{partial ^2 C}{partial x^2} + rxfrac{partial C}{partial x } qquad (5)$

Сведение уравнения БШ к уравнению теплопроводности

Получив дифференциальное уравнение БШ, вопрос о поиске его решения остается актуальным. Забегая вперед, окажется, что такое уравнение можно свести к дифференциальному уравнению теплопроводности, решение которого хорошо известно.

Процесс получения уравнения теплопроводности из уравнения БШ носит чисто аналитический характер. Преобразования начинаются с замены y = ln x . Делается это для того чтобы избавится от функцийи x^2 , которые стоят при первой и второй производных соответственно.

Переходя к новой переменной, дифференцируем по правилу сложной функции, после чегои x^2 сокращаются, а уравнение приобретает следующий вид:

$frac{partial C}{partial tau } + rC = frac{sigma^2}{2} frac{partial ^2 C}{partial y^2} + Rfrac{partial C}{partial y } qquad (6)$

где $R = r - frac{sigma^2}{2}$

Подробнее

Находим первую производную по, при условии

$frac{partial C}{partial x} = frac{partial C}{partial y} cdot frac{dy}{dx} = frac{partial C}{partial y} cdot frac{1}{x}$

Вторую производную по, при условии

$frac{partial ^2 C}{partial x^2} =left ( frac{partial C}{partial y} cdot frac{dy}{dx}right )_x '= (frac{partial C}{partial y})_x 'cdot frac{dy}{dx} + frac{partial C}{partial y} cdot (frac{dy}{dx})_x' = left( (frac{partial C}{partial y})_y' cdot y'right ) cdot y'+ frac{partial C}{partial y} cdot y'' =$ $= left( frac{partial^2 C}{partial y^2} frac{1}{x}right ) frac{1}{x} - frac{partial C}{partial y} frac{1}{x^2} = frac{1}{x^2}left ( frac{partial^2 C}{partial y^2} - frac{partial C}{partial y}right )$

Избавляемся оти

$frac{partial C}{partial tau } + rC = frac{sigma^2 x^2}{2} cdot frac{1}{x^2}left ( frac{partial^2 C}{partial y^2} - frac{partial C}{partial y}right ) + rx cdot frac{1}{x} frac{partial C}{partial y} Leftrightarrow frac{partial C}{partial tau } + rC = frac{sigma^2}{2} left( frac{partial ^2 C}{partial y^2} -frac{partial C}{partial y } right )+ rfrac{partial C}{partial y }$

Проводим дальнейшие преобразования для приведения к виду уравнения

$frac{partial C}{partial tau } + rC = frac{sigma^2}{2} left( frac{partial ^2 C}{partial y^2} -frac{partial C}{partial y } right )+ rfrac{partial C}{partial y } Rightarrow_1 frac{partial C}{partial tau } + rC = frac{sigma^2}{2} frac{partial ^2 C}{partial y^2} - frac{sigma^2}{2} frac{partial C}{partial y } + rfrac{partial C}{partial y } Rightarrow_2$ $frac{partial C}{partial tau } + rC = frac{sigma^2}{2} frac{partial ^2 C}{partial y^2} + (r - frac{sigma^2}{2}) frac{partial C}{partial y } Rightarrow_3 frac{partial C}{partial tau } + rC = frac{sigma^2}{2} frac{partial ^2 C}{partial y^2} + Rfrac{partial C}{partial y }$

где $R = r - frac{sigma^2}{2}$

Следующее преобразование намного менее приятное, однако в пару шагов приводит нас к уравнению теплопроводности. Для этого проводим замену: $C(e^y, tau) = e^{alpha y + beta tau} cdot U(y, tau)$ , а далее подбираем коэффициенты alpha и beta так, чтобы ряд членов уравнения взаимно сократились и мы получили искомое уравнение теплопроводности, представленное ниже:

$frac{partial U}{partial tau } = frac{sigma^2}{2} frac{partial ^2 U}{partial y^2} qquad (7)$

Подробнее

Подставляем $Ue^{alpha y + beta tau}$ вместо функциив исходное уравнение

$left (U e^{alpha y + beta tau} right )_tau ' + rUe^{alpha y + beta tau} = frac{sigma^2}{2} left (U e^{alpha y + beta tau} right )_{yy} '' + Rleft (U e^{alpha y + beta tau} right )_y ' qquad (*)$

Находим частную производную по

$left (U e^{alpha y + beta tau} right )_tau ' = frac{partial U}{partial tau} cdot e^{alpha y + beta tau} + U cdot left ( e^{alpha y + beta tau} right )_tau ' = frac{partial U}{partial tau} cdot e^{alpha y + beta tau} + beta U cdot e^{alpha y + beta tau}$

Находим первую частную производную по

$left (U e^{alpha y + beta tau} right )_y ' = frac{partial U}{partial y} cdot e^{alpha y + beta tau} + U cdot left ( e^{alpha y + beta tau} right )_y ' = frac{partial U}{partial y} cdot e^{alpha y + beta tau} + alpha U cdot e^{alpha y + beta tau}$

Вторую частную производную по

$left( { frac{partial U}{partial y}} cdot e^{alpha y + beta tau} + alpha U cdot e^{alpha y + beta tau} right)_y '= left( { frac{partial U}{partial y}} cdot e^{alpha y + beta tau} right)_y' + left (alpha U cdot e^{alpha y + beta tau} right )_y' =$ $left( { frac{partial^2 U}{partial y^2}}e^{alpha y + beta tau} + alpha frac{partial U}{partial y} e^{alpha y + beta tau} right) + left ( alpha frac{partial U}{partial y} e^{alpha y + beta tau} + alpha^2 U e^{alpha y + beta tau}right ) =$ $e^{alpha y + beta tau} left( frac{partial^2 U}{partial y^2} + 2alpha frac{partial U}{partial y} + alpha^2 U right)$

Подставляем найденные производные в уравнениеи делим обе части на $e^{alpha y + beta tau}$

$frac{partial U}{partial tau} + beta U + rU = frac{sigma^2}{2}left( frac{partial^2 U}{partial y^2} + 2alpha frac{partial U}{partial y} + alpha^2 U right) + Rleft ( frac{partial U}{partial y} + aU right )$

Теперь положим $alpha = -frac{R}{sigma^2}$ , а $beta = -(r + frac{R^2}{2 sigma^2})$ , тогда получим следующее уравнение:

$frac{partial U}{partial tau} - (r + frac{1}{2}frac{R^2}{sigma^2}) U + rU = frac{sigma^2}{2}left( frac{partial^2 U}{partial y^2} - frac {2R}{sigma^2} frac{partial U}{partial y} + frac{R^2}{sigma^4} U right) + Rleft ( frac{partial U}{partial y} - frac{R}{ sigma^2}U right )$

Раскроем скобки и приведем подобные слагаемые

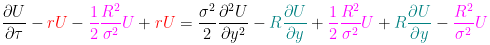
В итоге останется соотношение, которое является уравнением тепловодности

$frac{partial U}{partial tau } = frac{sigma^2}{2} frac{partial ^2 U}{partial y^2}$

Частным решением уравнения (7) является гауссиана:

$P(y, tau, y_0) = frac{1}{sigma sqrt{2 pi tau }} cdot exp(-frac{(y-y_0)^2}{2sigma^2 tau}) qquad (8)$

Это проверяется непосредственно путем вычисления частных производных (P)_tau ' , $(P)_{yy} ''$ и подстановки их в уравнение (7) .

Проверка решения

Для удобства введем следующее обозначение:

$e^{*} = exp(-frac{(y-y_0)^2}{2sigma^2 tau})$

Далее найдем частную производную по:

$frac{partial P}{partial tau} = left (frac{1}{sigma sqrt{2 pi tau }} right )_ tau ' cdot e^{*} + frac{1}{sigma sqrt{2 pi tau }} cdot left (exp(-frac{(y-y_0)^2}{2sigma^2 tau}) right )_tau ' =$ $- frac{1}{2sigma tau sqrt{2pi tau}} cdot e^{*} + frac{1}{sigma sqrt{2pi tau}}cdot e^{*} cdot frac{(y-y_0)^2}{2sigma^2 tau^2} = e^{*} left (frac{(y-y_0)^2}{2 sigma^3 tau^2 sqrt{2pi tau}} - frac{1}{2sigma tau sqrt{2pi tau}} right )$

Затем найдем первую и вторую производную по:

$frac{partial P}{partial y} = frac{1}{sigma sqrt{2pi tau}} cdot (e^{*})_y' = - frac{1}{sigma sqrt{2pi tau}} cdot e^{*} cdot frac{(y-y_0)}{ sigma^2 tau} Rightarrow$ $frac{partial^2 P}{partial y^2} = left (- frac{1}{sigma sqrt{2pi tau}} cdot e^{*} cdot frac{(y-y_0)}{sigma^2 tau} right )_y' = left (- frac{1}{sigma^3 tau sqrt{2pi tau}} cdot left ( e^{*} cdot (y-y_0) right ) right )_y' =$ $- frac{1}{sigma^3 tau sqrt{2pi tau}} cdot left[left( e^{*} cdot (-frac{(y-y_0)}{sigma^2 tau}) cdot (y-y_0) right ) + e^{*} cdot 1right] = e^{*} cdot left (frac{(y-y_0)^2}{sigma^5 tau^2 sqrt{2pi tau}} - frac{1}{sigma^3 tau sqrt{2pi tau}} right )$

Подставим обе найденные производные в уравнение (7) и сократим на e^* . В итоге получаем тождество:

$frac{(y-y_0)^2}{2 sigma^3 tau^2 sqrt{2pi tau}} - frac{1}{2sigma tau sqrt{2pi tau}} = frac{sigma^2}{2}left (frac{(y-y_0)^2}{sigma^5 tau^2 sqrt{2pi tau}} - frac{1}{sigma^3 tau sqrt{2pi tau}} right )$

Значит гауссиана (8) в самом деле является частным решением нашего уравнения теплопроводности.

В виду линейности уравнения теплопроводности, для любой непрерывной функции u(s) интеграл:

$int_ {-infty}^{+infty} u(s) P(y, tau, s)ds,$

зависящий от параметрови tau , будет также решением уравнения (7) , на самом деле — общим решением. Итак, общее решение уравнения (7) имеет вид:

$U(y, tau) = int_{-infty}^{+infty} u(s) P(y, tau, s)ds =frac{1}{sigma sqrt{2 pi tau }} int_{-infty}^{+infty} u(s) cdot exp left(-frac{(y-s)^2}{2sigma^2 tau}right)ds qquad (9)$

Вычисление начальных условий

Для получения окончательного решения по формуле (9) следует найти функцию u(s) . Мы намереваемся доказать, что u(y) = U(y;0) для любой точки. Короткий путь — воспользоваться тем, что при tau mapsto 0 гауссиана переходит в дельта-функцию Дирака delta (y-s) и тогда:

$U(y; 0) = int _{-infty}^{+infty}u(s) delta (y-s)ds = u(y)$

Объясним это подробнее путем применения первой теоремы о среднем: если функция f(x) непрерывна на отрезке [a;b] , и при этом функция g(x) не меняет знак и является интегрируемой, тогда существует такое число c in[a,b] , что:

$int_{a}^{b} f(x)g(x) dx = f(c) int_{a}^{b}g(x)dx$

Зададимся произвольно малым tau mapsto 0 «хвосты» $int_{-infty}^{y- varepsilon }, int_{y-varepsilon }^{+infty}$ могут быть сделаны сколь угодно малыми и тогда:

$U(y, tau) approx int_{y- varepsilon}^{y+ varepsilon} u(s) P(y, tau, s)ds$

Далее воспользуемся выше сформулированной теоремой о среднем и найдем d in [y-varepsilon; y+varepsilon ] такое, что

$int_{y- varepsilon}^{y+ varepsilon} u(s) P(y, tau, s)ds = u(d) int_{y- varepsilon}^{y+ varepsilon} P(y, tau, s)ds.$

Так как, $lim_{tau mapsto 0} int_{y- varepsilon}^{y+ varepsilon} P(y, tau, s)ds = 1$ , то $u(d) int_{y- varepsilon}^{y+ varepsilon} P(y, tau, s)ds approx u(d)$ . В силу того, что, получаем d mapsto y . Окончательно имеем:

Следовательно,

$u(y) = U(y;0) = e^{-alpha y}cdot C(e^{y}; 0) = e^{-alpha y} cdot max (e^y -x_s;0)$

Аналитическая формула БШ

Так как, max (e^y -x_s;0)=0 при условии y < ln x_s , то интеграл в правой части (9) сводится к виду:

$U(y, tau) = int_{ln x_s}^{+infty} (e^s - x_s)frac{e^{-alpha s}}{sigma sqrt{2 pi tau}} expleft(-frac{(y-s)^2}{2 sigma^2 tau}right)ds qquad (10)$

Дальнейшее интегрирование соотношения (10) позволяет найти функцию U(y;tau) , которая соотносится с функцией стоимости опциона, как $C(e^y, tau) = e^{alpha y + beta tau} cdot U(y, tau)$ . Следовательно, нахождение решенияавтоматически позволит найти функцию.

Решение сводится к разделению интеграла (10) на разность двух интегралов и приведению их к функции нормированного нормального распределения.

После процесса интегрирования, представленного ниже получим анализируемую нами функцию Блэка-Шоулза:

$C = x_0F left [ frac{ln(xe^{rtau} / x_s)}{sigma sqrt{tau}} + frac{sigma sqrt{tau}}{2} right ] - x_se^{-rtau}F left [ frac{ln(xe^{rtau} / x_s)}{sigma sqrt{tau}} - frac{sigma sqrt{tau}}{2} right ]$

где, функция нормированного нормального распределения,волатильность за единичный период.

Подробное решение

Осуществим необходимые замены, пересчитаем пределы интегрирования и вычислим дифференциал новой функции для соотношения:

$z = frac{(s-y)}{ sigma sqrt{tau}}; qquad s = zsigma sqrt{tau} + y qquad$ $z(ln x_s) = frac{ln x_s - y}{sigma sqrt{tau}} =: gamma text{ - новый нижний предел}$ $dz = left (frac{(s-y)}{2 sigma sqrt{tau}} right )' ds Rightarrow dz = frac{ds}{sigma sqrt{tau}} Rightarrow ds = sigma sqrt{tau}dz$

Переписываем интеграл с учетом ряда замен в новом виде:

$U(y, tau) =int_{gamma }^{+infty}left (e^{(1-alpha)(sqrt{tau} sigma z + y)} - x_s e^{-alpha(y + sqrt{tau}sigma z)} right ) frac{e^{-frac{z^2}{2}}}{sigma sqrt{2 pi tau}} sqrt{tau }sigma dz =$ $frac{1}{sqrt{2 pi }} int_{gamma }^{+infty}left (e^{(1-alpha)(sqrt{tau} sigma z + y) -frac{z^2}{2} } - x_s e^{-alpha(y + sqrt{tau}sigma z)-frac{z^2}{2}} right ) dz$

Далее представим имеющийся у нас интеграл в виде разности интегралов:

$U(y, tau) =frac{1}{sqrt{2 pi }}left [ int_{gamma }^{+infty}e^{(1-alpha)(sqrt{tau} sigma z + y)-frac{z^2}{2}} dz -int_{gamma }^{+infty} x_s e^{-alpha(y + sqrt{tau}sigma z)-frac{z^2}{2}} dz right ]$

Выделим полный квадрат в показателях экспонент и обозначим красным цветом члены, которые не зависят от переменной интегрирования.

Вынесем из под знака интеграла, выделенные красным цветом сомножители, после чего под интегралами, останутся функции, представимые в виде $e^{-frac{v^2}{2}}$ , а значит отмеченные синим выражения будут легко сводится к нормированному нормальному распределению.

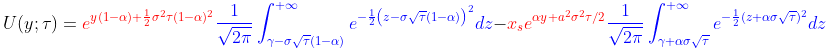
Обратим внимание на то, что в стандартном виде интеграл нормального распределения в качестве нижнего предела интегрирования содержит, а верхним пределом является аргумент функции. Следовательно, в нашем случае необходимо поменять местами пределы интегрирования. Для этого воспользуемся свойствами функции нормального распределения:

$frac{1}{sqrt{2 pi }} int_{gamma}^{+infty} e^{-frac{z^2}{2}}dz= F(-gamma) qquad (*)$

Также постараемся сделать нашу запись более компактной, для этого выше и далее обозначаем функцию нормального распределения через, а ее аргументы заменим буквой. В силу того, функция нормального распределения содержит в качестве аргументов разные выражения, будем различать их, каки. В итоге получим следующую запись:

где, $d_1 = -left(gamma - sigmasqrt{tau}(1-alpha)right)$ , а $d_2 =- left( gamma +alpha sigma sqrt{tau} right)$ , с учетом минусов от *.

Теперь требуется провести обратные замены для аргументови, а также для сомножителей, которые выделены красным цветом. Вспоминаем, какие замены нами осуществлялись:

$gamma =frac{ln x_s - y}{sigma sqrt{tau}} ; qquad alpha = -frac{R}{sigma^2}; qquad R = r -frac{sigma^2}{2};qquad y = ln x.$

После обратных замен аргументыив окончательном виде выглядят следующим образом:

$d_1 = frac{ln(xe^{rtau} / x_s)}{sigma sqrt{tau}} + frac{sigma sqrt{tau}}{2};qquad d_2 = frac{ln(xe^{rtau} / x_s)}{sigma sqrt{tau}} - frac{sigma sqrt{tau}}{2}.$

Остается решить вопрос с громоздкими сомножителями, которые стоят перед функциями нормального распределения. Так как мы ищем решение для цены опциона, то вспоминая замену, сделанную для сведения к уравнению теплопроводности $C(e^y, tau) = e^{alpha y + beta tau} cdot U(y, tau)$ , понимаем, что соотношение ** надо умножить на $e^{alpha y + beta tau}$ .

При умножении складываем показатели экспонент и приступаем к проведению обратных замен. В итоге окажется, что $e^{alpha y + beta tau} cdot e^{y(1-alpha ) + frac{1}{2} sigma^2 tau (1-alpha)^2}$ превратится в, а от $e^{alpha y + beta tau} cdot e^{{alpha y+ a^2sigma^2 tau /2 }}$ останется только $e^{-r tau}$ . Таким образом, итоговая формула БШ будет иметь следующий вид:

Список использованных источников

Степанов С.С. «Стохастический мир», 2009 г. — 376 с.
Пискунов Н.С. Дифференциальное и интегральное исчисление для вузов. Часть 2, глава ХХ. 1985 г. — 560 с.
Вентцель Е.С. Овчаров Л.А. Теория вероятностей и ее инженерные приложения. — М., ACADEMA, 2003. — 480 с.
Жуленев С.В. «Финансовая математика. Введение в классическую теорию. Часть 2.», 2012 г. — 419 с.
Ширяев А.Н. «Основы стохастической финансовой математики. Том 1. Факты. Модели», 1998 — 512 с.