Продолжаю цикл статей, в котором публикую наработки к занятиям математического кружка. Это не учебник и не решебник, а пример жанра, который, в своё время был назван математическими этюдами. В моём случае источником тем являются либо интересные вопросы ребят, либо мои провокации в виде «дурацких» вопросов, на которые очень хочется ответить стандартными фразами типа: «По определению.», «Так сложилось исторически.» или «Не задавайте глупых вопросов!».
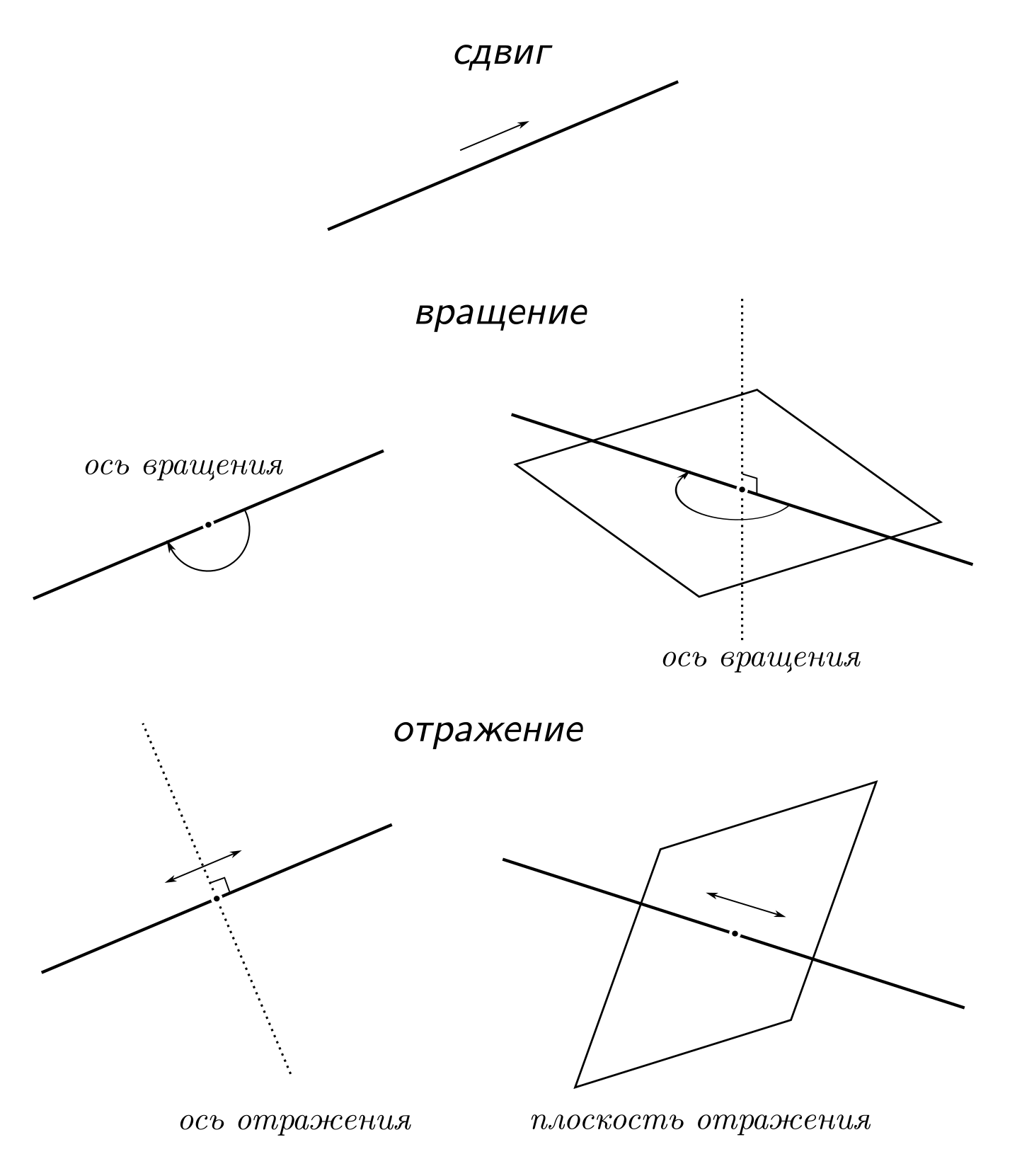
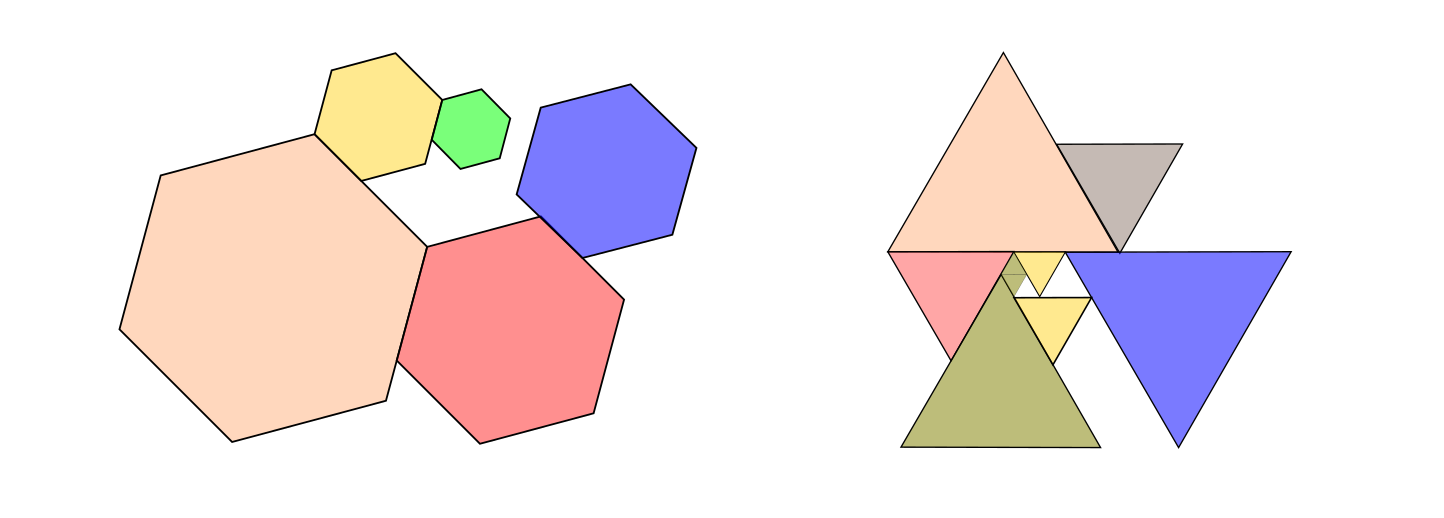
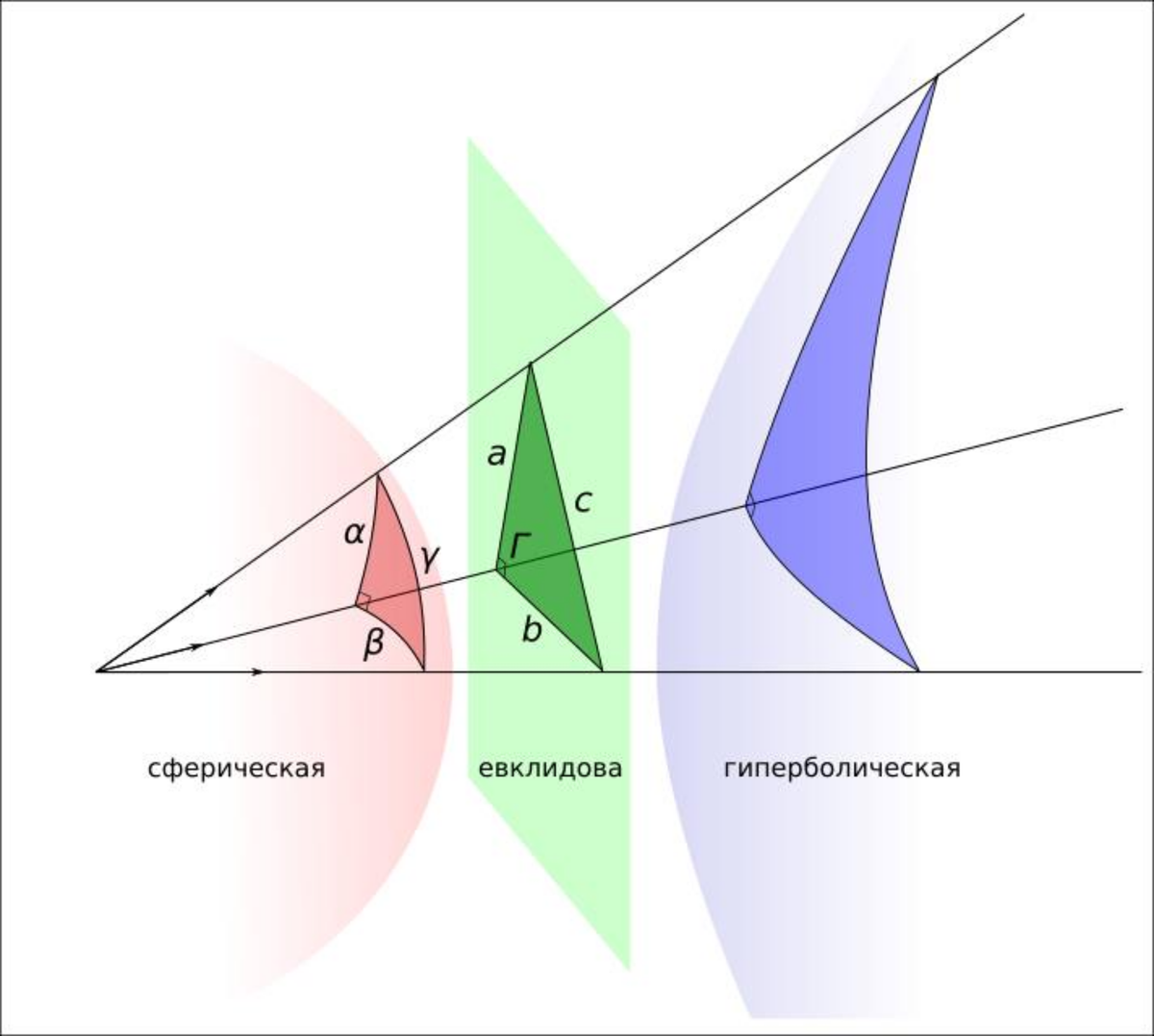
Эта статья посвящена такому вопросу: «Что делает особенным прямой угол, он же 90°, он же π/2?» После некоторой дискуссии удалось выделить с десяток ответов: Прямой угол тесно связан с понятиями «вертикаль» и «горизонталь», естественными в мире, где существенную роль играет гравитация. С горизонтальной поверхности (перпендикулярной вертикали) ничего не соскальзывает и не скатывается. Наконец, ребята совершенно справедливо связали это с устойчивостью конструкций. Прямоугольники и параллелепипеды позволяет просто компактно и достаточно экономно упаковывать на плоскости и пространстве однотипные объекты. Тут в качестве аргументов выдвигается мебель и всевозможные коробки. Под прямым углом пересекаются декартовы координатные оси и в двух и трёх измерениях. Теорема Пифагора работает именно для прямоугольных треугольников. Если освещать площадку под прямым углом к ней (вдоль нормали), то поток света окажется больше, чем для любого другого угла. Проекция (условно говоря, тень) всякого отрезка на какую-либо прямую обращается в ноль, если угол между ними прямой. Только для перпендикулярных прямых вертикальные и смежные углы, ими образуемые, равны между собой. Расстояние от всякой точки до какой-либо прямой минимально в направлении, перпендикулярном к этой прямой. Всякая касательная к окружности перпендикулярна радиусу, проходящему через точку касания. Биссектриса развёрнутого угла перпендикулярна его сторонам. Я хочу выделить одно свойство, про которое можно было бы сказать вольным парафразом Толкиена: «Одно, чтоб править всеми, Оно главнее всех, Оно соберёт всех вместе, И заключит в себе.» (В оригинале: «И заключит во тьме», но так как я убеждён, что знания — это свет, я решил от тьмы избавиться). А дальше, выделив это свойство, мы попробуем вывести из него все прочие. Такой своеобразный bootstrapping — не заложение основ математики или какая‑то педагогическая методика. Это упражнение в связывании между собой разных аспектов, в складывании элементов математической мозаики, и в «подвешивании» дерева рассуждений за различные узлы. В первую очередь, конечно же, для удовольствия. Здесь имеются в виду «Начала» Евклида — одна из самых читаемых книг в истории. В самом начале этого труда, в книге первой, в первой главе, определение прямого угла дано под номером 10: Когда же прямая, восстановленная на прямой, образует рядом углы, равные между собой, то каждый из равных углов есть прямой, а восставленная прямая называется перпендикуляром к той, на которой она восставлена. Кроме того, среди знаменитых пяти евклидовых постулатов, четвёртым числится такой: [Предположим] что все прямые углы равны между собой. Получается, в качестве основного свойства прямого угла, Евклид приводит свойство, которое мы уже упомянули под номером 7. Но он на этом не останавливается, а считает необходимым предположить ещё, что прямые углы получаются одинаковыми при любых обстоятельствах. И в этом видится не столько свойство углов, сколько свойство прямых. В математике есть ряд концепций, которые, с одной стороны, понятны и доступны кому угодно, а с другой, ведут к очень глубоким и общим выводам, правда, совсем не очевидными, и порой, очень сложными путями. Одна из таких концепций — симметрия. В школе мы знакомимся с этим понятием симметрии (зеркальная, центральная и т. д.), но почти их не используем, разве что, на олимпиадах. На первых двух курсах физического факультета НГУ, где я учился, всё чаще и чаще стала появляться фраза: «из соображений симметрии», позволяющая легко решить сложную задачу. И, вдруг, на третьем курсе появилась теория групп, и все прочие дисциплины: теория поля, уравнения математической физики, аналитическая механика и квантовая механика, перешли на язык симметрии и групп. Он позволил связать воедино всё, что изучалось прежде, и говоря на этом языке, преподаватели могли выражать такие вещи, от которых у меня, как у студента, появлялись мурашки восторга. Симметрия позволила увидеть и понять теорему Стокса, а вместе с ней «устройство» законов Кулона и Ньютона, знакомых со школы; теорема Нёттер связала симметрии с законами сохранения в физике; группы симметрий сферических функций объяснили периодический закон Д. И. Менделеева и устройство таблицы элементов; другие группы привели в порядок «зоопарк» элементарных частиц; группы, образуемые движениями прямой, круга и плоскости привели к более полному пониманию что такое число. Симметрия, конечно же, не единственная фундаментальная концепция, но она такая понятная и такая красивая! Поэтому я сформулирую базовое свойство прямого угла так: Всякая ось симметрии всякой прямой перпендикулярна этой прямой (образует прямой угол). Я не хочу сказать, что это свойство «главное» или наиболее фундаментальное. Оно мне нравится тем, что его легко понять и проверить, а также тем, что оно опирается на одно из красивейших и наиболее универсальных понятий современной математики — симметрию. Симметрия — это свойство объекта сохранять какие-то свои характеристики при некотором преобразовании. Среди всевозможных преобразований в евклидовой геометрии выделяются изометрии: преобразования, сохраняющие все расстояния и углы. Существует три вида изометрии: сдвиг, поворот и отражение. Первые два, не меняющие ориентации фигур, называются движениями. Прямая имеет симметрии связанные со всеми изометриями. Она совпадает сама с собой и при сдвиге вдоль неё (трансляционая симметрия), и при повороте вокруг произвольной точки на развернутый угол (вращательная симметрия), и при отражении (зеркальная симметрия). При сдвиге ни одна точка не остаётся на месте. При повороте на плоскости, неподвижной остаётся одна точка, а в пространстве — прямая, называемые осью вращения. Неподвижные точки при отражении принадлежат прямой (оси отражения) на плоскости, или плоскости отражения в пространстве. Таким образом, свойство: «всякая ось симметрии всякой прямой перпендикулярна ей» включает все случаи и ось вращения, и ось отражения. Из неподвижности оси отражения и совпадения прямой при отражении, незамедлительно следует определение данное Евклидом: угол между прямой и осью симметрии и смежный ему должны быть равны, поскольку лучи, образующие оба эти угла при этом преобразовании совпадают с самими собой. Нам неважно какая это прямая, неважно в пространстве какой размерности мы её рассматриваем, неважно через какую точку на прямой проходит ось, в любом случае угол между прямой и её осью симметрии всегда один и тот же. Таким образом группа симметрии прямой говорит нам, что предположение Евклида о том, что все прямые углы равны справедливо. Симметричными могут быть не только геометрические фигуры. Само отношение между двумя прямыми: «прямая Из этого соображения следует вывод: две перпендикулярные прямые имеют кроме зеркальной симметрии, вращательную симметрию четвёртого порядка. Это обстоятельство позволяет очень точно построить прямой угол с помощью приёмов оригами: достаточно сложить вдвое лист бумаги, согнув его в любом направлении, а затем сложить его ещё раз так, чтобы первая складка наложилась сама на себя. Теперь мы можем понять почему задачу упаковки пространства мы предпочитаем решать именно с помощью прямых углов. Вращательная симметрия четвёртого порядка приводит к тому, что многоугольник, образуемый отрезками, подходящими друг к другу под прямыми углами, будет иметь четыре вершины, а вращательная симметрия второго порядка, присущая прямой, гарантирует попарную параллельность сторон многоугольника. Попарная параллельность это большой плюс при упаковке, так как добавление одного прямоугольного объекта к другому с любой стороны не изменяет основных направлений сторон получившегося многоугольника. Более того, все внешние углы будут равны или кратны внутренним и упаковку можно будет продолжить. Даже если прямоугольники будут различными, все они сохранят ориентировку сторон и равенство углов. Замощения любыми другими фигурами приводят к большему разнообразию углов и ориентаций. Правильные шестиугольники, как известно, тоже неплохо замощают плоскость, однако промежутки между ними правильными шестиугольниками заполнить уже не получится. А вот треугольники с этой задачей справляются не хуже прямоугольников. А всё потому, что линейным преобразованием (скашиванием) можно замощение прямоугольниками превратить в замощение параллелограммами, а потом их уже можно разбить на треугольники. Но делать коробки в форме треугольных пирамид разного размера не удобно из-за гравитации: всё будет скатываться и разъезжаться. Но об этом поговорим чуть позже. Напомню ещё раз: в основе евклидовой геометрии лежат изометрии — преобразования, сохраняющие расстояния между точками. Какой бы смысл мы ни вкладывали в понятие расстояния, для него должно выполняться правило треугольника. Это правило можно вольно толковать так: длина ломаной кривой не может быть меньше длины отрезка, соединяющего её концы. Рассмотрим прямую и две точки, одну на прямой ( Отражение сохраняет все расстояния, значит Расстояние От одной единственной точки можно перейти к кратчайшему расстоянию между двумя непересекающимися прямыми на плоскости или в пространстве, а также к кратчайшему расстоянию между точкой и плоскостью. Во всех этих случаях, кратчайшими будут расстояния, измеряемые вдоль осей симметрии получающихся систем (двух непересекающихся прямых в пространстве, точки и плоскости). Окружность — одна из самых симметричных фигур, имеющая бесконечное число осей отражения и бесконечное число вращательных симметрий. Одно из определений окружности, которое мне очень по душе — это геометрическое место точек плоскости, переходящее само в себя при произвольном повороте относительно одной выделенной точки или оси. Такое определение работает и в пространстве, и даже за пределами евклидовой геометрии, например, на сфере. Но кроме вращательной симметрии, окружность имеет и симметрию отражения, причём, как и у прямой, осей отражения у неё бесконечно много. Все оси отражения окружности проходят через её центр (поскольку они должны переходить друг в друга при повороте). Значит, радиусы и диаметры окружности принадлежат её осям отражения. Каждая такая ось пересекает окружность в двух точках, и через каждую такую точку можно провести линию, симметричную, относительно оси — касательную к окружности. Касательная имеет с окружностью одну общую точку и обладает той же симметрией отражения, что и окружность (по построению), отсюда делаем общий вывод: любая касательная к окружности перпендикулярна своей оси симметрии, а следовательно, и принадлежащему ей радиусу. Это объясняет почему при вращении дохлой крысы на верёвочке, мгновенное перемещение (и скорость) крысы будет всегда перпендикулярно радиусу вращения. К такому же выводу можно прийти, вычисляя производные от радиус-вектора, как это делается в механике, но приведённые тут рассуждения полезны для интуитивного понимания кругового движения. Рассматривая в пространстве все возможные повороты окружности и касательной к ней вокруг их общей оси симметрии, мы из окружности получим сферу, а из касательной — плоскость, касающуюся сферы. Так мы приходим к выводу, что любая прямая, принадлежащая касательной плоскости, перпендикулярна радиусу сферы. Как жители поверхности сферы, любое направление, принадлежащее касательной плоскости мы называем горизонтальным, а направление вдоль оси симметрии сферы — вертикальным. Математики называют эти направления тангенциальным и нормальным. Тут стоит заметить, что касательная плоскость к сфере, которой принадлежат горизонтальные линии, не содержит в себе линию горизонта, которая лежит на самой сфере и является линией пересечения конуса касающегося сферы с вершиной в точке наблюдения. Так что горизонт всегда оказывается несколько ниже горизонтальной, то есть, касательной плоскости. Притяжение идеальной шарообразной планеты приводит к тому, что направление силы тяжести на её поверхности будет всегда направлено к центру шара, вдоль её радиуса. Это направление мы договорились считать вертикальным и оно будет нормально горизонтальной площадке. А что с телами иной формы, или с системами тел? Тут нам простой геометрией уже не обойтись, и нужно обратиться к теории поля и привлечь несколько более сложное понятие: эквипотенциальную поверхность. Представьте себе, как из системы точек выходят, возможно, изгибаясь силовые линии. Вдоль них будет направлена сила притяжения в любой заданной точке пространства. Если мы окружим эту систему точек жидким океаном, то уровень воды постарается выровняться таким образом, чтобы любое перемещение вдоль его поверхности было всегда перпендикулярно силовым линиям. В любой точке на поверхности такого океана мы легко можем сказать где вертикальное, а где горизонтальное направления. Это и есть эквипотенциальная поверхность. Поверхность нашей Земли не является эквипотенциальной, хоть и очень близка к ней. На ней есть горы, холмы и впадины, отклоняющиеся от эквипотенциали, которые «держатся» на прочности горных пород. По этой причине строителям и геодезистам приходится искать горизонталь в каждой отдельной точке Земли инструментально. Но если мы её отыскали, скажем, пузырьковым уровнем, то можем быть вполне уверены в том, что ровно в этом месте сила тяжести направлена нормально к горизонтально расположенному уровню. Эквипотенциальные поверхности для сложных конфигураций масс, конечно же уже строятся не из соображений симметрии. Координаты любой точки на плоскости можно определить, проведя две произвольные координатные прямые, имеющие единственную общую точку, совпадающую с началами координат на обеих прямых. Угол между этими прямыми и длина их единичных отрезков могут быть произвольными, лишь бы они были отличны от нуля. Любые две нетривиальные оси позволяют однозначно указать координаты любой точки плоскости, так что перпендикулярность осей для координатного метода не критична. Однако линейно растягивая пространство вдоль одной из этих осей, мы неизбежно изменим наклон другой и координатная система изменится. И только если одна ось будет осью симметрии другой (и, как мы понимаем, наоборот) растяжения и сжатия одной из них никак не изменит другой: ни её направления, ни длины единичного отрезка. Эти две координатные системы оказываются линейно независимыми или ортогональными. В таких системах смена единиц измерения производится простым умножением координат на число, без необходимости компенсировать взаимные искажения осей поворотом или скашиванием. Об ортогональности мы подробно поговорим в следующем разделе, а пока заметим, что предыдущие рассуждения относились к прямолинейным координатам, и основывались на группе симметрии прямой. При использовании симметрии окружностей, мы получим полярные координаты, в которых координатные линии: концентрические окружности и радиальные лучи всюду пересекаются так, что касательные к окружностям оказываются перпендикулярны лучам. Так что полярные координаты являются криволинейной ортогональной координатной системой. Если симметрия рассматриваемых задач оказывается более сложной, есть возможность перейти к иным ортогональным криволинейным координатам: эллиптическим, параболическим, сферическим и прочим. Некоторые из них показаны на рисунке: Такие координатные системы используют в математической физике, в теории поля, в теории упругости и других разделах математики и физики, в которых исследуются функции, областью определения которых является всё пространство. Во всех этих случаях выбор и построение системы координат определяется симметрией пространства или решаемой задачи. Полярные координаты отражают симметрию окружности или цилиндра; параболические — симметрию прямолинейного луча (кончика иглы, тонкой антенны или края тонкой плоской пластины); биполярные координаты — симметрию тора; эллиптические — симметрию тонкого круглого диска в трёхмерном пространстве. Во всех приведённых системах координатные кривые во всех точках пересечения имеют перпендикулярные касательные. Это приводит к тому, что локально (в малой окрестности неособых точек) ортогональные системы неотличимы от привычных нам прямоугольных координат. Это становятся по-настоящему удобным для вычисления расстояний и площадей, а также для определения дифференциальных операторов, так что становится возможным описывать сложные поля линейными дифференциальными уравнениями для криволинейных задач. Пора, наконец, серьёзно поговорить о том что же мы имеем в виду, говоря об углах. Это понятие в геометрии неразрывно связано с направлением, а оно, в свою очередь, наиболее полно выражается через векторы. Геометрический вектор, как направленный отрезок, характеризуется длиной и направлением и обе эти величины можно выразить через скалярное произведение векторов. Скалярное произведение мы обычно выражаем через координаты векторов, однако использование координатной системы само опирается на скалярное произведение, как на более фундаментальное понятие. Важно, что результатом скалярного произведения двух векторов является число, то есть, скалярная величина, не зависящая от выбора системы координат. Кроме этого, скалярное произведение линейно (билинейно), это значит, что оно дистрибутивно по отношению к сложению: Имея для некоторого векторного пространства корректно определённое скалярное произведение, можно определить длину или норму вектора, как произведение вектора Как бы мы ни определили произведение с такими свойствами, для него должно выполняться неравенство Коши-Шварца-Буняковского: Существует много доказательств этого неравенства, любопытные могут познакомиться с ними на странице Википедии. Нас в нём интересуют два крайних случая: Первый соответствует сонаправленным, или коллинеарным векторам, а второй — ортогональным или линейно независимым. Векторное пространство, как и скалярное произведение, можно определить, не привязываясь ни к какой геометрии. Так, например, в гильбертовых пространствах точками (векторами) являются функции, а роль скалярного произведения может выполнять некоторое интегральное преобразование от произведения этих функций. В частности, функции Ни о каких «углах между функциями» при этом речь не идёт, ортогональность более общее понятие, чем геометрическая перпендикулярность. Для тех кому кажется, что скалярное произведение и ортогональность функций это какая‑то заумь, замечу, что с этим связаны мощные инструменты анализа функций и решения дифференциальных уравнений. Метод Фурье позволяет подобно тому, как мы раскладываем вектор на компоненты в некотором базисе, раскладывать функции в ряды Фурье, используя базисы ортогональных функций. А теорема Штурма‑Лиувилля позволяет строить такие базисы для дифференциальных операторов в упомянутых выше криволинейных ортогональных координатах. Но вернёмся к геометрии. Со времён Феликса Клейна и Давида Гильберта геометрии определяются группой преобразований, сохраняющих те или иные фундаментальные свойства геометрического пространства. Евклидова геометрия строится на группе изометрий — преобразований, сохраняющих расстояния между всеми точками. От расстояния (метрики) мы ждём того, что оно не будет меняться при параллельных переносах, и произвольных поворотах относительно произвольной точки, отражениях относительно произвольных прямых, а также любых комбинаций этих преобразований. Если перебирать всевозможные способы ввести метрику на векторном пространстве, то выяснится, что только евклидова метрика будет сохраняться при любом из перечисленных преобразований. В этой метрике расстояние между точками Рассматривая повороты, мы вводим некий числовой (скалярный) параметр, который и называем углом поворота. При этом мы требуем, чтобы этот параметр был аддитивным, то есть, чтобы композиция поворотов на углы Под поворотом Никакие свойства этой функции нам сейчас не понадобятся, поскольку нас не интересует конкретная угловая мера, достаточно того, что такая функция существует. Для нас важно заметить, что функция угла (и сам угол) между ортогональными векторами, для которых скалярное произведение равно нулю, не будет изменяться при произвольной смене знака любого из векторов, что геометрически соответствует зеркальному отражению, меняющему угол на смежный ему. А раз при отражении угол между ортогональными векторами не меняется, то это означает, что такие векторы образуют угол, равный своему смежному, то есть, единственный и неповторимый прямой угол. Так мы и приходим к выводу: ортогональные геометрические векторы перпендикулярны друг другу. Имея скалярное произведение векторов, позволяющее определить метрику, не зависящую от изометрий, из базового свойства скалярного произведения — линейности, можно прийти к теореме косинусов, а значит, и к теореме Пифагора. Если рассмотреть два вектора Таким образом, из евклидовости пространства следует, что соотношение Пифагора в треугольнике выполняется тогда и только тогда, когда векторы построенные на двух сторонах ортогональны, что в свою очередь, означает, что треугольник прямоугольный. Евклид смог доказать это в своих «Началах», используя чисто геометрические построения, мы сегодня прошли этот путь, практически минуя геометрию, опираясь на понятия созданные Августином Коши, Феликсом Клейном и Давидом Гильбертом А что творится за пределами Евклидовой геометрии? Неужели магия прямого угла там не работает? Прямой угол в нашем понимании остаётся прямым и на сфере и в гиперболическом мире, но несмотря на это, в знакомом нам виде теорема Пифагора перестаёт работать в неевклидовых геометриях: квадраты катетов уже не обязаны складываться в квадрат гипотенузы. Однако, есть такое обобщение теоремы Пифагора, которое способно работать вне конкретной двумерной геометрии, но для этого нужно перейти из метрической геометрии в проективную. В проективном подходе треугольник превращается в трёхгранный угол, образованный тремя плоскостями, пересекающимися в одной точке, как показано на рисунке. Такой угол представляет многообразие всех треугольников, проективно эквивалентных заданному. Представьте себе, что проективный треугольник это лучи света, исходящие из его вершины, как из кинопроектора. Если мы поставим на их пути какое‑либо двумерное пространство, как экран, то получим двухмерный треугольник, но не обязательно привычный нам. Получить «нормальный» треугольник можно, пересекая этот проективный треугольник плоскостью, но если экран будет искривлён, то мы сможем получить треугольники в тех или иных неевклидовых геометриях. Но пока мы не фиксировали конкретную геометрию, размеры и расстояния не играют роли, важны только их отношения или углы, либо функции от них. Конечно же, мы схитрили, вложив всё это построение в трёхмерное евклидово пространство, так что трёхгранный угол можно характеризовать тремя плоскими углами при вершине где Мы получили нечто гораздо более сложное, чем теорема Пифагора, или обобщающая её теорема косинусов. «Висящая» в некотором векторном пространстве трехгранная пирамида с заветной формулой, сияющей рядом, существует «сама по себе», без привязки к какой‑либо конкретной геометрии. Мы уже знаем, что угол между ортогональными векторами всегда равен прямому углу. В теореме Пифагора фигурируют прямоугольные треугольники, которые при переходе к проективной геометрии превратятся в такие трёхгранные углы, у которых угол Красиво, правда? Это проективное представление великой теоремы и оно весьма лаконично, хоть и не столь понятно. Давайте рассмотрим сферическую геометрию. Если в вершину трёхгранного угла-треугольника поместить сферу с уравнением здесь А что если поместить в вершину проективного треугольника не сферу, а двухполостный гиперболоид Здесь функция
Начнём с «Начал»

О симметрии
Симметрии прямой
Почему дома, вагоны и коробки прямоугольные?
является осью симметрии для прямой
» является симметричным: из него вытекает, что и прямая
является осью симметрии для прямой
. В школьном учебнике зеркальное отражение плоскости относительно прямой определяют как перенос точек плоскости вдоль линий, перпендикулярных оси отражения с сохранением расстояний между точками и осью. Теперь мы в состоянии разобраться, почему это определение именно такое. Симметричность отношения «быть осью симметрии» приводит к тому, что прямая является осью симметрии для всех своих осей симметрии, а они проходят через все точки рассматриваемой плоскости.
Почему расстояние от точки до прямой вычисляется вдоль перпендикуляра?
), другую — вне её (
). Предположим теперь, что
и есть кратчайшее расстояние между этими точками. Проведём через точку
ось симметрии прямой и воспользуемся симметричностью отношения «быть осью симметрии», отразив ось симметрии относительно прямой, и получив отражение точки
: точку
.
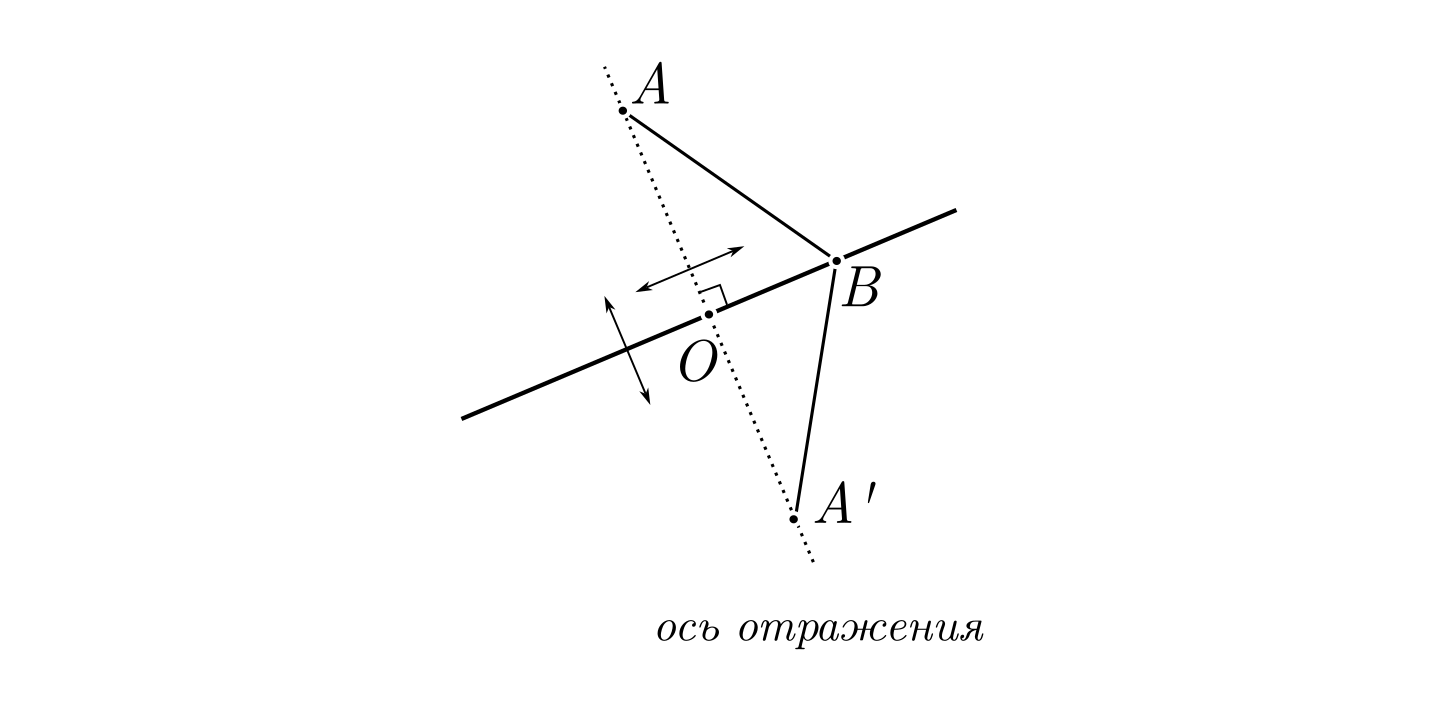
,
. Согласно правилу треугольника, длина ломаной
не может превышать расстояния между её концами
:
может быть кратчайшим, только если
. То есть, минимальным будет расстояние, измеряемое именно вдоль оси симметрии, то есть, вдоль перпендикуляра к прямой.
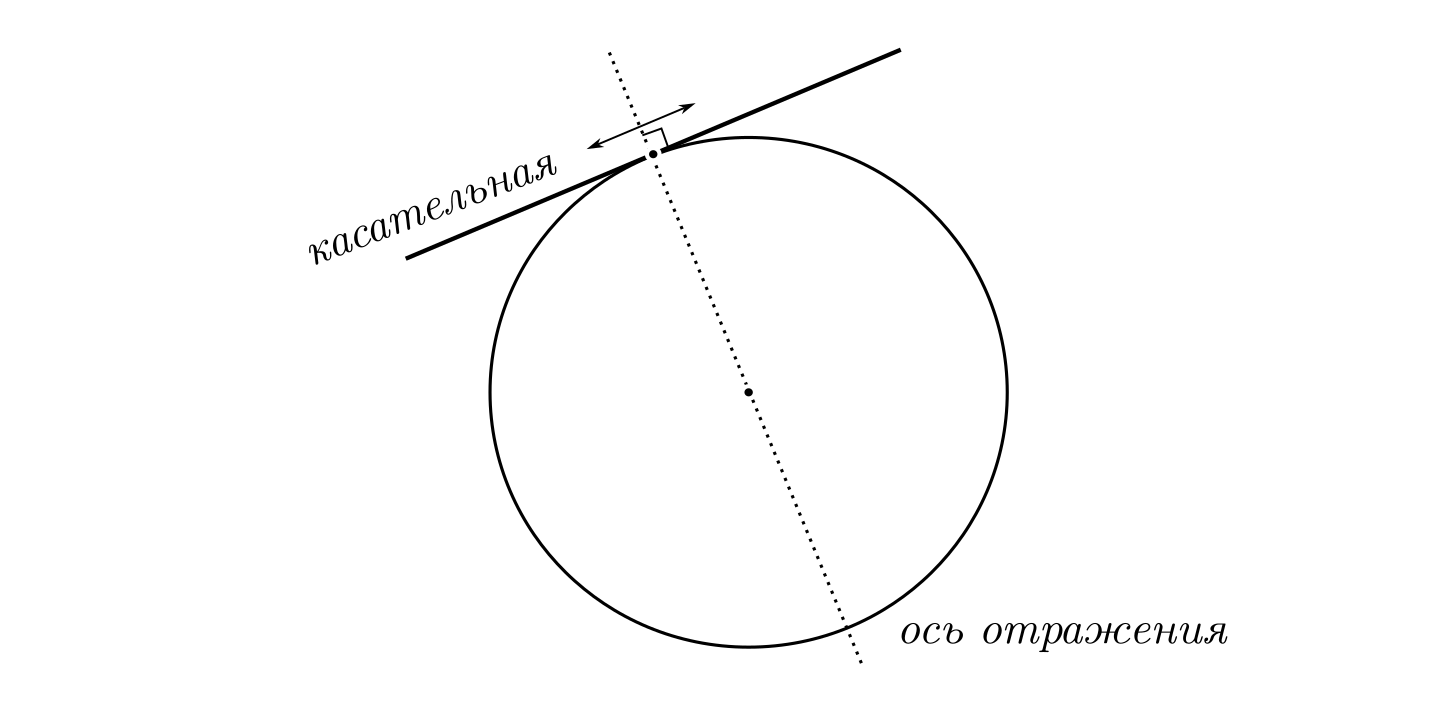
Почему радиус окружности перпендикулярен касательной?


Почему с горизонтального стола ничего не скатывается?
Почему декартовы координатные оси перпендикулярны друг другу?

Что же такое угол?
и при умножении любого из векторов на некоторое число, произведение тоже должно увеличиться на эту же величину:
на самого себя:
из которого для ненулевых векторов следует, что
и
ортогональны, поскольку равно нулю их скалярное произведение, определённое как.
и
равно длине вектора, соединяющего эти точки:
и
была эквивалентной повороту на угол
:
при этом понимается преобразование, изменяющее направление, но не длину вектора. Это значит, что должна существовать некая обратимая скалярная (не зависящая от выбора системы координат) функция, которая позволит переводить повороты в углы:
Эта функция
, связывающая угловую меру между векторами с их скалярным произведением, нам хорошо знакома, под именем косинус. Отсюда и берётся хорошо известное выражение:
и
, и вычислить квадрат длины их разницы, то получим следующее выражение:
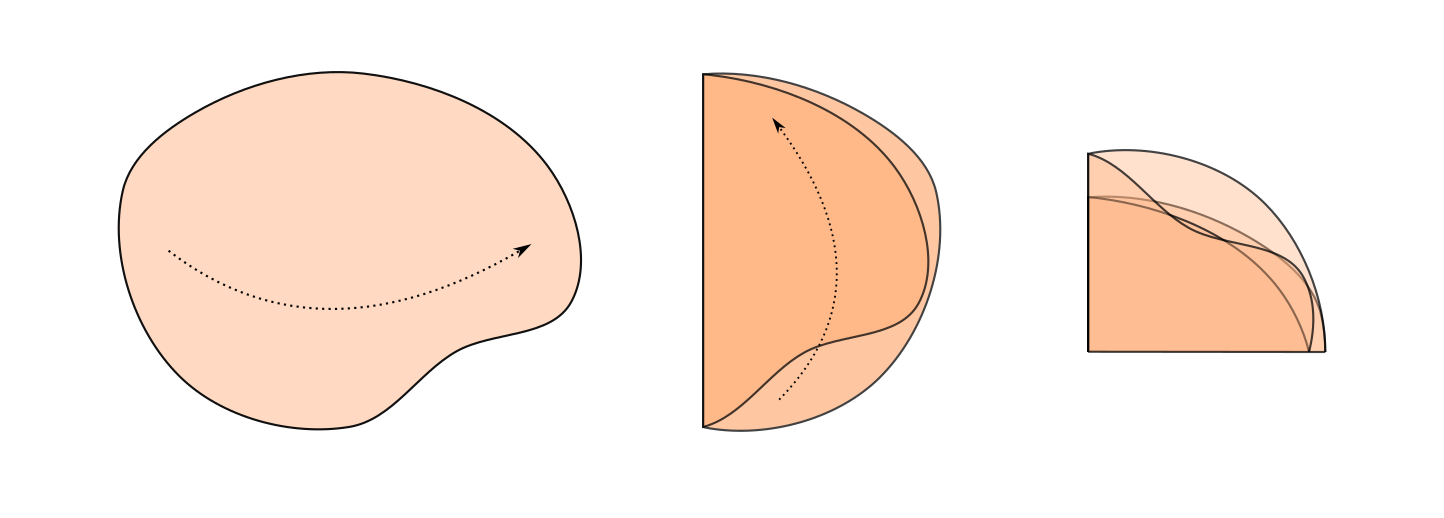
От Евклидовой геометрии к проективной
,
и
или тремя векторами. Вновь, используя только векторную алгебру, можно вывести весьма общее соотношение на углы, которое выполняется для всех нетривиальных трёхгранных углов:
— ещё один плоский угол, показанный на рисунке. Это соотношение называется сферической теоремой косинусов.
прямой. Кроме того, мы знаем, что косинус прямого угла равен нулю, так что правая часть сферической теоремы косинусов превращается в самый обобщённый вид теоремы Пифагора. Вот он:
, то пересекаясь с ней, трёхгранный угол образует прямоугольный треугольник. Для него обобщённая теорема Пифагора примет следующий вид:
,
и
— уже длины сторон треугольника на конкретной проекции. Не больно-то по-пифагоровски выглядит это соотношение, но как мы уже говорили, квадраты катетов на сфере уже никому ничего не должны, а это соотношение универсально! А давайте рассмотрим ма-а-аленький треугольник на огро-о-омной сфере, то есть сделаем отношения сторон треугольника к радиусу малыми величинами. Это позволит нам воспользоваться разложением косинуса в ряд:
Подставив это приближение в обобщённую теорему Пифагора и отбросив слагаемые четвёртого порядка, мы получим плоскую евклидову теорему Пифагора
как приближение сферической.
? Не буду проводить вас через дебри алгебры (не очень сложные, если использовать комплексные числа), и сразу скажу, что в гиперболической геометрии теорема Пифагора примет гиперболический вид:
— косинус гиперболический. И конечно же, для маленьких треугольников, таких что
мы вновь получим привычную евклидову формулировку чудесной теоремы.
Математическое продолжение: Самый корректный угол
Паблик ВКонтакте
Последние посты
- Google отключает AdSense для пользователей из Белоруссии и прекращает выплаты блогерам с YouTube
- Заметки об обновлении Farming Simulator 25, версия 1.4.0.0
- Wildberries запускает функцию «виртуальной примерки» мебели в реальном времени
- Сервис по вызову такси Yandex Go запущен в Турции
- В «СберЗдоровье» внедрили ИИ-ассистента с использованием GigaChat


