Давайте посмотрим, насколько понятно устроена природа, и как просто это можно доказать, при этом познакомимся с мифами, в которые зачастую верят геофизики (хотя их учили совершенно противоположному, как будет показано ниже). Откройте учебники и статьи по геофизике и вы увидите там преобразования Буге, разложения по сферическим функциям и другие термины, заимствованные из разных наук. При этом, преобразование Буге придумано 300 лет назад для анализа результатов нескольких десятков измерений, а форма нашей планеты далека от сферической настолько, что все глобальные модели оперируют эллипсоидами. Все это наследие чрезвычайно затрудняет понимание простых и очевидных, в общем-то, вещей и явлений.
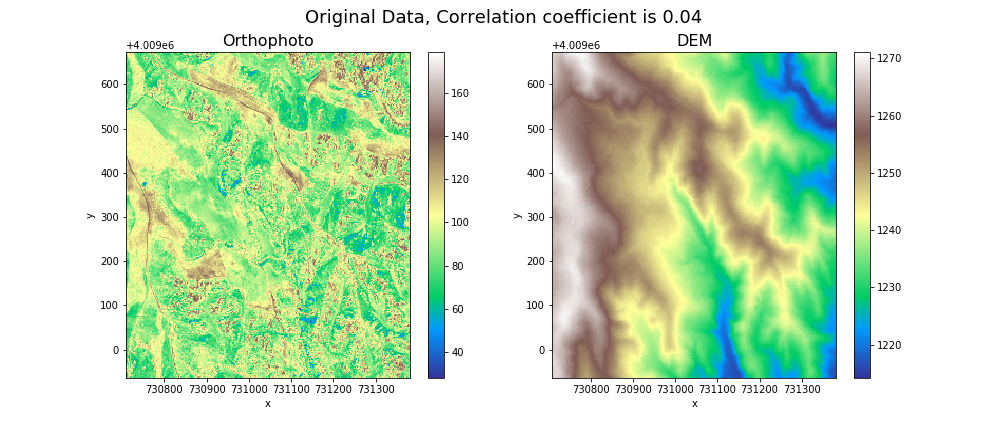
Видите взаимосвязь ортофотоснимка и рельефа? Если да, то вы или геолог или можете им стать: корреляция компонентов (разложения в пространственный спектр) составляет 41% для длины волны 20 м, 58% для 50 м и 99% для 300 м (Jupyter Python ноутбук с вычислениями доступен по ссылкам ниже). Большинство геофизиков поклянутся, что «это у вас спектры порченые» (записано с натуры), игнорируя и геофизику и прилагаемые вычисления и ссылки на публикации.
Миф первый, рельеф и сила тяжести
Одним из краеугольных мифов является следующий, смотрите к примеру русскоязычную страницу википедии Изостазия (возможно, после публикации моей статьи викистраницу поправят):
Важнейшим доказательством изостазии является отсутствие связи между рельефом и силой тяжести.
Увы, именно в отсутствие такой связи верят многие из встреченных мной геофизиков (но не геологи), хотя это абсолютно неверно! Что интересно, в англоязычной версии этой же викистраницы написано прямо противоположное, смотрите пример с айсбергом в разделе «Deposition and erosion»:
An analogy may be made with an iceberg, which always floats with a certain proportion of its mass below the surface of the water. If snow falls to the top of the iceberg, the iceberg will sink lower in the water. If a layer of ice melts off the top of the iceberg, the remaining iceberg will rise. Similarly, Earth’s lithosphere «floats» in the asthenosphere.
Этот пример очень наглядный — когда надводная часть айсберга уменьшается из-за его таяния, то при этом и весь айсберг постепенно всплывает и уменьшается, а если надводная часть увеличивается из-за намерзания снега сверху, то айсберг оседает и подводная часть тоже увеличивается. Таким же образом, земная литосфера вместе с рельефом на ней плавает в астеносфере. Вероятно, из русскоязычной статьи это простое и понятное объяснение убрали только потому, что оно явно противоречит рассматриваемому мифу…
Посмотрим, что говорит оглавление русскоязычного учебника по геофизике (Викулин, 2004):
Глобальные волны геоида, отсутствие их связи с особенностями строения земной коры…
Здесь глобальные волны геоида — это изменения (аномалии) поля силы тяжести порядка масштабов планеты, для которых, как и указано, отсутствует связь с рельефом. В то же время, для всех компонентов силы тяжести меньшего масштаба эта связь есть! Могу лишь предположить, что студенты-геофизики зачастую не понимают смысла выражения «глобальные волны геоида» (кстати, для обработки спутниковых данных современные глобальные модели оперируют «изменяющимся во времени квазигеоидом» с явным указанием порядка волны…).
Более того, корреляция компонентов силы тяжести (или вертикальной компоненты гравитационного поля) и рельефа близка к 100%, как показано в работе «Radially symmetric coherence between satellite gravity and multibeam bathymetry grids» (Marks and Smith, 2012). На графике ниже график радиальной когеренции (справа) из указанной статьи дополнен мною двумерной коррелограммой (слева) для глобальной модели гравитационных аномалий Sandwell and Smith Gravity Anomaly и глобальной модели рельефа GEBCO 2019:
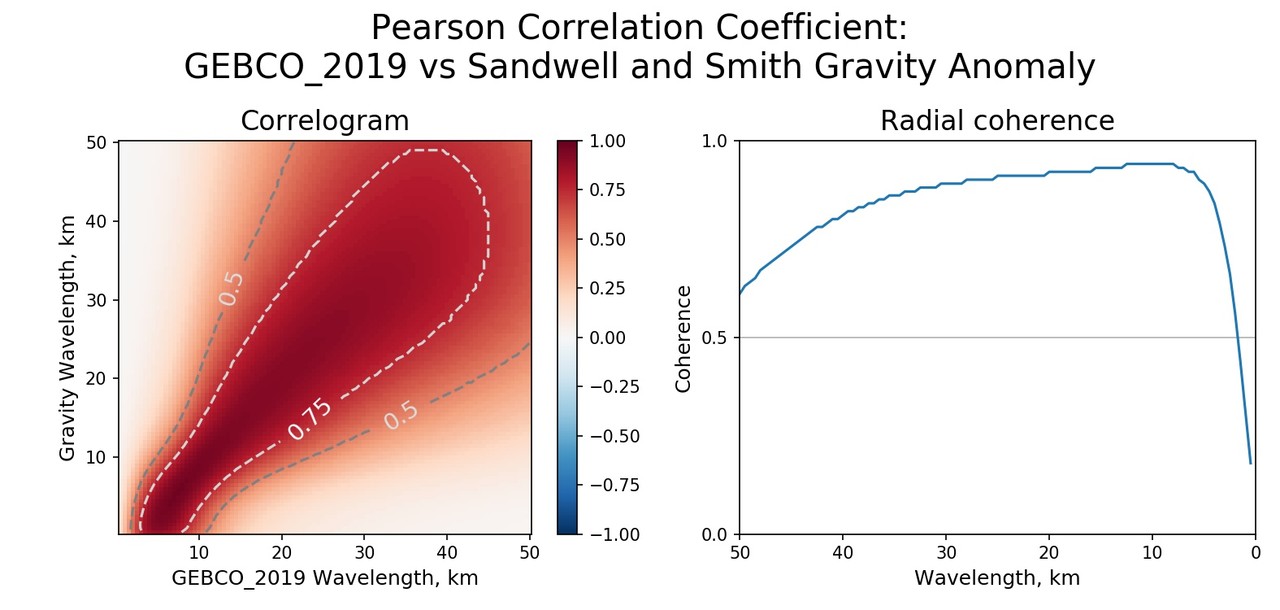
Если на графике радиальной когеренции (корреляции) не понятно, почему для первых километров масштаба связь компонентов мала, то на двумерной коррелограмме все становится ясно — измеренная сила тяжести относится к поверхности океана, а топография, очевидно, ко дну. Таким образом, здесь мы видим, что до масштабов ~40 км корреляция компонент близка к 100%. Более того, для региона Индонезия высокая корреляция (>75%) наблюдается до масштабов в сотни километров и средняя (>50%) для масштабов в тысячи километров, как показано в статьях по ссылкам ниже.
Миф второй, рельеф и аномалия Буге
Что интересно, миф второй полностью противоречит первому, что не мешает многим геофизикам верить в оба разом. Встречайте Аномалию Буге (Бугера):
Аномалия Бугера — расхождение между теоретически вычисленным и реальным значением гравитационного поля Земли в определённой точке референц-эллипсоида.
В этом определении сразу кроется подвох (и даже не один — на самом деле, речь идет про вертикальную компоненту гравитационного поля) — как, неужели мы настолько плохо вычисляем гравитационное поле Земли? На самом же деле, задача состоит в выделении относительно малых аномальных составляющих, соответствующих геологическим объектам, из измеренных значений силы тяжести. Предлагается это делать в два шага, или две редукции:
Редукция Бугера называется простой или неполной, если местность можно приближенно представить в качестве бесконечной плоскости.
Очевидно, что с высотой (удалением от планеты) сила тяжести уменьшается, поэтому наблюдаемые (измеренные) на разной высоте значения силы тяжести нельзя сопоставить напрямую. Вот Буге и придумал способ, как удалить эту разницу из-за изменения высоты точки наблюдения (измерения), вычитая некую константу, домноженную на высоту точки наблюдения. Конечно, использование модели плоской Земли создает огромную ошибку при обработке современных точных данных, об этом я уже писал на Хабре в статье Почему в 21 веке геофизики верят в теорию плоской Земли?
И следующий шаг, или редукция:
Уточнённая, или полная редукция Бугера позволяет полностью учесть влияние рельефа местности.
Здесь речь о том, что наличие на местности неровностей в виде возвышений или углублений влияет на измеренную в этих местах силу тяжести, так что для сравнения измеренных значений нужно и их компенсировать. Заметим, что такая поправка, то есть необходимость учитывать влияние рельефа местности на силу тяжести, очевидно противоречит первому мифу. И эта поправка Буге проста в использовании — нужно было среднюю плотность пород умножить на высоту точки наблюдения (возможно, Буге и до интеграла по глубине бы додумался, только где ему было взять среднюю плотность пород на территории в зависимости от глубины). Для самого Буге, с учетом расстояния между точками наблюдения километров 20 и более, о большой точности речь не шла, и средняя плотность собранных им же геологических образцов по региону его вполне устраивала для вычисления поправки. Увы, для современных детальных измерений этот метод совсем никуда не годится.
Посмотрим практический пример, как компоненты силы тяжести глобальной модели WGM2012 после редукции Буге (слева) и еще одной редукции (справа) коррелируют с компонентами рельефа глобальной модели GEBCO 2019:

Как видим, про «полностью учесть рельеф местности» речь тут явно не идет — то есть результат редукции Буге противоречит его определению, а значит, его использование неправомерно. Обратим внимание на правый график — тут мы ожидаем максимум корреляции 100%, а наблюдаем всего около 75%, что показывает неточность самой модели WGM2012 (по сравнению с использованной выше Sandwell and Smith Gravity Anomaly, авторы которой вовсе не вычисляют редукцию Буге по уже понятным причинам), таким образом, здесь реальная корреляция редукции Буге с рельефом получится около -100%.
Если обратиться к учебнику «Гравиразведка» (Утёмов, 2009), там в соответствующем разделе есть разъяснение полученного результата:
Большую роль при вычислении аномалий Буге играет правильный выбор плотности промежуточного слоя. При слишком завышенной, либо слишком заниженной плотности получается отрицательная, либо положительная корреляция поля и высотных отметок.
Таким образом, раз мы получили отрицательную корреляцию, проблема кроется в завышенной плотности, использованной для построения модели. Если же уменьшать значение этого параметра, то для коротковолновых компонент (начало графика) корреляция станет сильно положительной. Таким образом, для правильного вычисления редукции Буге необходимо априори иметь детальную плотностную модель всей территории, включающую в себя все геологические аномалии, что, очевидно, делает обсуждаемую редукцию Буге полностью бесполезной.
Лучшим путем представляется использование полосовой пространственной фильтрации для выделения аномалий искомого масштаба, в этом случае и решение обратной задачи (восстановление плотности геологической среды по значениям силы тяжести на поверхности) получается однозначным. Также используется приведение измеренных значений к единому уровню (обычно, уровню моря) разными методами.
Миф третий, сферический конь эллипсоид в вакууме
Этот миф «элитный» — только для тех геофизиков, кто вообще запомнил про существование сферических функций. Действительно, функции такие существуют и даже используются (в математической физике), но в практической геофизике они вообще-то не нужны. Посмотрим русскую викистраницу Геопотенциальная модель:
В геофизике модель геопотенциала представляет собой теоретический анализ измерения и расчета эффекты Земли гравитационного поля
Да-а, «расчета эффекты Земли» это, конечно, не совсем русский язык, или даже совсем не русский. Равно как и «теоретический анализ измерения» тоже тот еще шедевр. Тем не менее, можно понять, что модель геопотенциала это модель (глобального) гравитационного поля Земли. Это определение уже ошибочное — на самом деле, рассматривается вертикальная компонента гравитационного поля, то есть сила тяжести (гравитационное поле векторное, а сила тяжести скалярная, и связь между ними весьма сложная). Но, главное, геофизикам такая модель вообще не нужна! А кому нужна, описано дальше в этой же викистатье:
Рекурсивные алгоритмы, используемые для численного распространения орбит космических аппаратов
Несмотря на коверканный русский язык, здесь все верно — глобальная модель силы тяжести необходима для запуска космических аппаратов. Теперь понятен и смысл разложения по сферическим функциям — так удобнее для вычисления круговых орбит (спутников) вокруг нашей планеты. Каким образом этот раздел теоретической физики попал в учебники геофизики, уму непостижимо, но, на мой взгляд, не удивительно, что геофизики вообще не поняли, что это и зачем.
В реальности же геофизики занимаются задачами локальными — поиском полезным ископаемых, планированием инженерных сооружений, предсказанием ущерба от стихийных бедствий наподобие извержения вулкана,… И для локального представления поля силы тяжести его (глобальное) сферическое разложение абсолютно не применимо — в принципе нельзя получить глобальную модель по данным на отдельно взятой территории. А применимы различные пространственные разложения такие, как преобразование Фурье, вейвлет-преобразование и так далее. И здесь мы подходим к следующему мифу.
Миф четвертый, о пространственных спектрах
У меня в коллекции есть такие перлы, как «спектры у вас порченые» (освятить, что ли, хотят?) и другие. Попросту говоря, геофизики не имеют никакого понятия, что это такое.
Давайте посмотрим, как же практически работать с пространственными спектрами. Как всегда в математике, все эти преобразования по сути чрезвычайно просты. Например, результат применения гауссова фильтра масштаба N метров есть низкочастотная фильтрация (low-pass filter), разница между исходным изображением и фильтрованным есть высокочастотная фильтрация (high-pass filter) и разница между двумя фильтрами масштаба N и M метров есть полосовая фильтрация (band-pass filter). Для выделения компонента пространственного спектра шириной l метров для длины волны L метров достаточно выполнить полосовую фильтрацию с фильтрами масштаба L-l/2, L+l/2. Спектр мощности может быть представлен как стандартное отклонение полученных компонент, а через логарифм спектра мощности посчитана и фрактальная размерность. Для примера посмотрите график радиальной когерентности из статьи НАСА и двумерную спектрограмму, полученную указанным методом, в обсуждении первого мифа выше.
Низкочастотная фильтрация это улучшенная замена Буге преобразования:
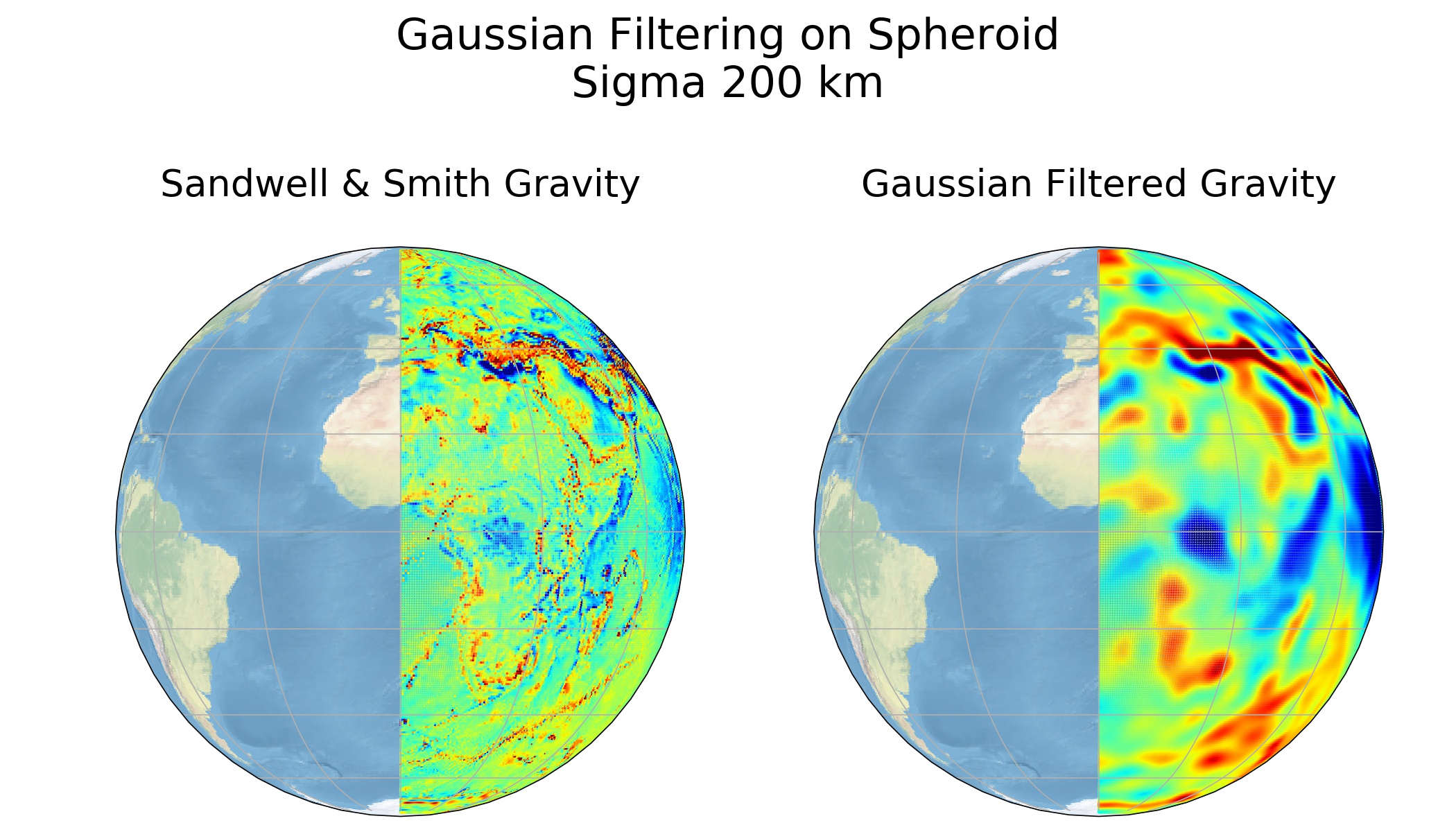
А если выполнить высокочастотную фильтрацию, то мы сразу получаем все глобальные разломы — то есть границы литосферных плит и микроплит:
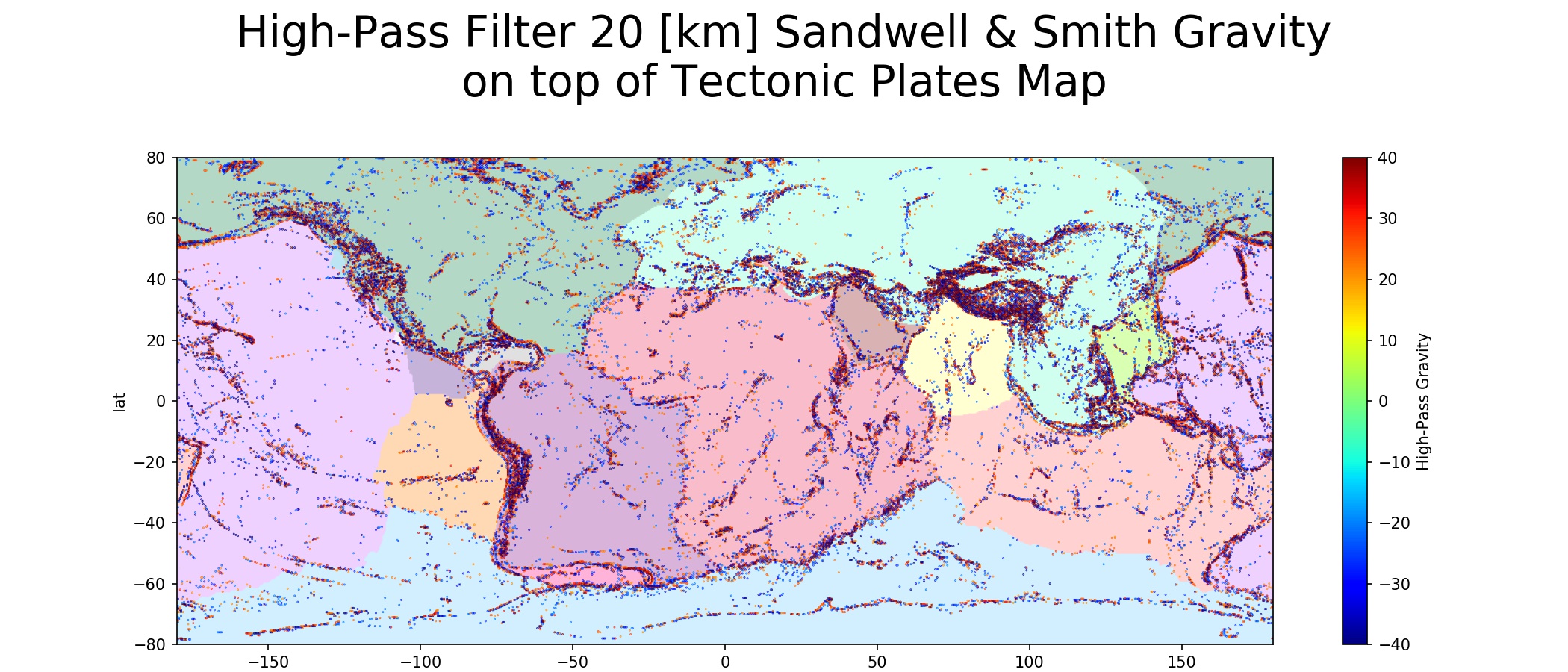
У специалистов может возникнуть вопрос, зачем стоит использовать (относительно медленную) матричную свертку для вычислений вместо, скажем, быстрого Фурье-преобразования (БПФ). Так вот, плюсы такого подхода заключаются в том, что при вычислении свертки мы можем корректно обрабатывать пропущенные значения (игнорировать их, а не использовать значение-заполнитель, и одновременно подсчитывать количество, считая результат неопределенным при большом числе пропущенных значений) и границы и даже работать с разреженными данными.
Интересно, что аргентинские геофизики применяют индекс фрактальности для вычисления средней плотности по территории в зависимости от глубины для использования в преобразовании Буге. В самом деле, этот способ работает для территории Латинской Америки (и не только там, но не везде по миру — все зависит от характера профиля плотности) — я проверил с помощью численного моделирования, по ссылкам ниже вы найдете готовый Jupyter Python ноутбук с вычислениями. А вот глобальные модели гравики для Латинской Америки с помощью сферических разложений получаются очень так себе (впрочем, для космических вычислений это не мешает, там не нужны детальные пространственные компоненты силы тяжести на уровне поверхности) — слишком высока фрактальность территории (сильно расчлененные горы с их отрогами), видимо, потому и пришлось придумывать фрактальный метод анализа.
Заключение
Мифы живучи, и чтобы не бороться с их носителями, давно придуманы различные обходные маневры. Например, некоторые российские геофизики мелким шрифтом указывают, что они использовали полосовую фильтрацию результатов преобразования Буге (если посмотреть на график выше, они просто удаляют ту часть графика, где корреляция отлична от нуля) — хотя нужна здесь просто полосовая фильтрация. Что касается связи компонент силы тяжести с рельефом (и с космоснимками), то в русскоязычных статьях просто избегают об этом упоминать, просто показывая результаты обработки космоснимка или рельефа как поля силы тяжести и вовсе не поясняя, каким образом эти данные связаны между собой.
Бонус
И специальное дополнение для мифоборцев. Не стал добавлять еще один миф, просто «на закуску» приведу выдержку из рецензии, когда-то полученной от журнала «Отечественная геология»:
Авторы пытаются нас убедить в том, что математические манипуляции с оптическим сигналом одного из каналов мультиспектральной съемки позволяют нам анализировать глубинное строение Земли. Математические обработки мультиспектральных снимков направлены на улучшение их визуального восприятия и классифицирования представленных на них объектов для создания тематических карт.
Так что учтите — если вы ссылаетесь на результаты из публикаций, скажем, НАСА (аналогично корреляции между пространственными спектрами рельефа и гравиметрии посчитав таковую между рельефом и космическими снимками) то будете обвинены в ереси («математических манипуляциях») и все ваши «порченые спектры» придется немедленно освятить (боюсь, путем окунания компьютера в чан со святой водой и никак иначе). Я предупредил! 🙂
Ссылки
Marks, K.M., Smith, W.H.F., 2012. Radially symmetric coherence between satellite gravity and multibeam bathymetry grids. Mar Geophys Res 33, 223–227. https://doi.org/10.1007/s11001-012-9157-1
Викулин А.В., 2004. ВВЕДЕНИЕ В ФИЗИКУ ЗЕМЛИ. УЧЕБНОЕ ПОСОБИЕ ДЛЯ ГЕОФИЗИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ ВУЗОВ
Утёмов Э.В., 2009. Гравиразведка
Spectral Coherence between Gravity and Bathymetry Grids
WGM2012 spatial components of free-air gravity and topography correlation
Bouguer and Free-Air Gravity Anomalies in terms of spatial spectrum
There is a high correlation between DEM and ortho photos
3D Density Inversion by Circular Hough Transform [Focal Average] and Fractality Index
[Gaussian Filtering on Spheroid [Sandwell & Smith]](

