Это перевод статьи Элиезера Юдковского, из научно-популярного цикла, посвященного многомировой интерпретации квантовой механики. Начало цикла было переведено на хабре, но потом переводчик видимо подустал. Его можно понять — материал очень объемный. Юдковский любит растекаться мыслию по древу. С другой стороны, материал действительно сложный, а повторение разными словами одного и того же позволяет картинке в голове неподготовленного читателя хоть как-то уложиться. Я не возьмусь продолжить перевод всего цикла, но попробую перевести пару наиболее важных статей.
Я пропущу статьи цикла про пространства состояний (классическое и квантовое) — концепция используется много где, и должна быть знакомой технически подготовленному читателю. А также пропущу фейнмановские интегралы по траекториям — с ними можно ознакомиться в прекрасном научно-популярном первоисточнике.
А вот следующий пост отвечает на важный вопрос. Если «настоящий» мир на фундаментальном уровне — квантовый, где все запутано, и все влияет друг на друга, откуда вообще берутся классические системы? Почему «естественные» квантовые явления мы видим так редко в обычной жизни? Это то что автор называет «классической галлюцинацией». Почему, например, создателям квантовых компьютеров нужно прикладывать такие огромные усилия, чтобы сохранить систему в «естественном» запутанном состоянии?
Disclaimer: я не являюсь ни профессиональным физиком, ни профессиональным переводчиком (также как и автор оригинала).
Декогеренция
Чтобы понять квантовый процесс под названием «декогеренция», сначала нужно понять как разрушается особое состояние квантовой независимости — то есть как именно квантовая система переходит из состояния независимости в состояние запутанности.
Квантовая независимость, как мы помним, это особое, «прямоугольное» состояние распределения амплитуды, которое хорошо факторизуется. То есть его можно представить как произведение распределений составных частей системы, которые выглядят для нас как «отдельные частицы».

Робкие туристы, посещающие наш квантовый мир, иногда принимают отсутствие такого «прямоугольного» распределения за некую особую таинственную связь между частицами. Отсюда — неудачный термин «квантовая запутанность». На самом деле, любая эволюция квантовой системы обычно порождает запутанность из независимости (а не наоборот), превращая прямоугольные распределения в не-прямоугольные. Независимость встречается редко и ее очень легко разрушить.
Чтобы лучше понять, какие именно физические процессы ведут к запутанности, начнем с классической системы. На рисунке изображена система из положительно заряженного лёгкого шарика на верхней дорожке и отрицательно заряженного тяжелого шарика на нижней дорожке. Изначально два шарика находятся далеко друг от друга и почти не взаимодействуют. Потом мы опускаем верхнюю дорожку, сближая шарики так, чтобы они начали притягивать друг друга (противоположные заряды притягиваются). И легкий шарик подкатывается к тяжелому (и тяжелый чуть-чуть подкатывается к легкому, подобно тому как падающее яблоко чуть-чуть притягивает к себе Землю).
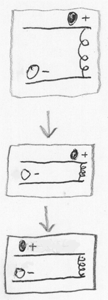
Теперь посмотрим на эту систему как на квантовую, с точки зрения фейнмановских интегралов по траекториям. То есть редставим эволюцию системы в виде суммы всех возможных траекторий от исходного состояния в пространстве конфигураций. Допустим два шарика вначале квантово независимы, их совместное распределение амплитуд можно представить как произведение «распределения для нижнего шарика» и «распределения для верхнего шарика».
Далее, пусть амплитуда нижнего шарика в начале состоит из трёх частей (которые с точки зрения интегралов Фейнмана можно рассматривать как три начальных состояния). Когда мы опускаем верхнюю дорожку, верхний шарик должен притянуться к нижнему. Но если совместная амплитуда нижнего шарика состоит из нескольких частей, то и в конце мы получим совместное распределение, состоящее из нескольких частей, каждый из которых описывает новое положение шариков.

Я всеми силами пытаюсь избегать формулировок типа «нижний шарик может находиться в одном из трёх мест» или «в каждом возможном случае верхний шарик притягивается к соответствующему положению нижнего». Хотя наверное вы все равно представите все именно так. С конце концов я сам это так проиллюстрировал. Я нарисовал три возможные начальные позиции и три возможных результата. Что поделать, так человеческий мозг обычно представляет себе интегралы Фейнмана. Но это не означает, что существуют три возможных состояния вселенной. Это просто трюк для визуализации интеграла по траекториям. Все три компонента амплитуды существуют в нашей вселенной, все три одинаково реальны, а вовсе не возможны или вероятны.
Теперь представьте, что вначале амплитуда нижнего шарика «размазана» по всей дорожке. Амплитуда верхнего шарика по-прежнему сосредоточена в одном месте. Тогда совместное распределение вначале будет в виде вытянутого прямоугольника, а затем превратится в диагональное.

По оси Х здесь — положение верхнего шарика, по оси Y — нижнего. Мы начинаем с точно локализованного верхнего шарика и «размытого» нижнего и заканчиваем на взаимозависимом распределении, когда обе координаты размыты, но равны друг другу (упрощённо). То есть изначально факторизуемое распределение превратилось в «запутанную систему» — оно больше не разлагается на два независимых множителя.
(Важное замечание:
Заметьте, что на рисунке выше развитие системы подчиняется второму закону термодинамики, он же теорема Лиувилля. При изменении системы сохраняется «размер облака», то есть общий объём амплитуды или проще говоря — размер серой области на графике. Если бы в начале на рисунке был огромный светло-серый квадрат (когда обе частицы сильно размазаны по пространству), то по второму закону термодинамики, он не смог бы превратиться в темно-серую диагональ. Чтобы перейти в состояние запутанности, система изначально должна обладать низкой энтропией, и эта энтропия не должна сильно увеличиться в процессе.
Напомню, что взаимная информация — это энтропия с противоположным знаком. Квантовые амплитуды — это не совсем информация, но принцип тот же. Начальная амплитуда должна быть достаточно сконцентрированной, чтобы породить компактную диагональную линию, вместо большого разреженного облака. Если представить, что распределение амплитуды имеет «квантовую энтропию», то энтропия запутанной системы должна быть относительно низкой)
Наконец мы готовы поговорить о декогеренции.

Система на рисунке довольно сильно запутана. Её можно описать примерно так: «есть две частицы, и они обе могут быть либо тут, либо там». Да, я сформулировал это, как будто есть два возможных состояния, а не физически реальное распределение амплитуды. Серьезно, я не знаю как по-нормальному описывать квантовую физику на обычном языке! Просто запомните общее правило, что «возможность» или «вероятность» — это сокращённое обозначение «физически существующего участка распределения амплитуды». Тогда я смогу описывать амплитуды гораздо короче, используя термины неопределенностей. Но помните, что это всего-лишь условность! «Частица либо здесь, либо там» обозначает «физически существующее распределение амплитуды из двух частей, одна здесь, одна там», а не «частица находится в одном из двух мест, но мы не знаем в каком».
Итак. Работать с запутанными системами обычно сложно (для физиков, конечно, не для вселенной). Вначале мы должны рассчитать все возможные траектории для всех возможных начальных условий (то есть учесть все физически существующие траектории амплитуды в интеграле Фейнмана). Далее, нужно учесть влияние этих траекторий друг на друга (вероятные в строгом смысле траектории взаимодействовать не могут — только нечто реально существующее может влиять на что-то ещё). К примеру, наши две частицы встречают ещё 20 других, каким-то образом взаимодействуют, и в результате получается куча конфигураций на которые повлияли все предыдущие точки всех возможных состояний.
Отметим, что запутанность возникает только если участки начальной амплитуды находятся недалеко друг от друга. Так чтобы пути их развития смогли пересекаться. Если две частицы находятся либо тут либо там, но «тут» и «там» у нас разделены расстоянием в два световых года, то их дальнейшие траектории могут пересечься не раньше чем через год.
Теперь добавим третью частицу. На рисунке показано трёхмерное пространство конфигураций, которое разлагается на независимые двухмерное и одномерное подпространства. То есть на две запутанных частицы и одну независимую от них.
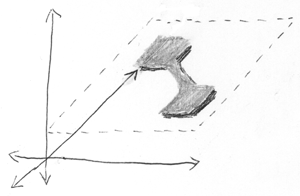
Высота — это третья частица, ширина и глубина — две запутанные частицы.
Независимая частица находится в определенном месте — по вертикали распределение очень узкое. Две запутанные частицы находятся либо тут, либо там (я опять использую некорректные вероятностные термины, вроде «определенный» и «либо», но вы понимаете о чем я).
Представим теперь, что третья частица реагирует с запутанными двумя неким образом, который чувствителен к их положению. Например, третья частица балансирует на острой вершине, две частицы пролетают мимо, притягивают ее, и она сваливается либо в одну, либо в другую сторону. После этого амплитуда выглядит как-то так.

Третья частица теперь запутана с двумя другими. И амплитуда теперь состоит из двух удалённых друг от друга кусков. Упрощенное описание: «если две частицы находились тут, то третья частица полетела сюда. А если они находились там, то она полетела туда.» То есть амплитуда стала полностью запутанной. Она больше не разлагается на независимые подпространства.
Но два куска амплитуды теперь дальше друг от друга, и каждый состоит из трёх частиц в соответствующей области. Это произошло потому, что третья частица чувствительна к координате других. После скатывания с острой вершины в одну из двух сторон, расстояние между конечными координатами достаточно велико.
На самом деле скатывание с вершины необязательно. Все работает аналогично, если у вас есть двадцать частиц, реагирующих на первые две и запутывающихся с ними. Окончательное распределение в 22-мерном пространстве будет выглядеть как две области, каждая из которых соответствует 22-м частицам. И расстояние между этими областями будет огромно. А чем больше расстояние, тем менее вероятно, что области в будущем повлияют друг на друга.
Это и есть декогеренция. Она является третьей причиной «классической галлюцинации», потому что две области начинают развиваться независимо. Это позволяет описывать их как не-запутанные системы. Как только мы рассмотрим их по-отдельности, распределение в каждой из них выглядит «прямоугольно» и независимо по трём координатам (я попытался показать это на рисунке выше).
В квантовом компьютере очень сложно предотвратить декогеренцию. Квантовые вычисления требует чтобы участки амплитуды оставались близко друг к другу и могли взаимодействовать. Но вокруг находятся триллионы других частиц, которые все время пытаются ненароком прореагировать с нашими хрупкими кубитами, разрушая точно сконструированную амплитуду.
И вы не можете просто взять и восстановить разрушенное. Для этого потребуется вернуть на место все прореагировавшие частицы, включая случайные частицы из окружения (не забудьте, итоговая амплитуда имеет совместное с ними распределение).
(Выглядит как практически необратимый процесс, правда? Вроде попытки собрать разбитое яйцо обратно в скорлупу. На самом деле это хорошая аналогия.
Вот почему я подчеркнул ранее, что процесс запутывания начинается с низкой энтропии. Декогеренция необратима, потому что это по сути термодинамический процесс.
Один из фундаментальных физических принципов гласит, что можно «прокрутить кинопленку назад» без нарушения фундаментальных законов. Если вы снимете на плёнку падающее на пол яйцо, а потом прокрутите ее задом наперёд, так что разбитое яйцо подлетает вверх с пола, собираясь при этом обратно в гладкую скорлупу, вы не увидите нарушенным ни одного физического закона. Все молекулы просто окажутся в нужном месте в нужное время, и яйцо отскочит от пола целым и невредимым. Это не невозможно, просто крайне маловероятно.
Тоже самое относится и к разбитой на удаленные куски амплитуде, неожиданно возвращающейся обратно в когерентное состояние — это теоретически возможно. Но практически нет шансов, что разобщённые вначале куски вдруг окажутся одновременно рядом друг с другом. Обратный процесс гораздо более вероятен.
На самом деле, в дополнение к прокручиванию пленки назад, нужно ещё поменять заряды всех частиц на противоположные, а также поменять местами лево и право (или одно из двух других измерений), превращая вселенную в её зеркальное отражение. Это правило известно как «CPT-инвариантность» от слов Заряд (Charge), Четность (Parity) и Время (Time).
Скорее всего CPT-инвариантность является одним из наиболее базовых принципов функционирования вселенной. Для физиков, попытки ее нарушить выглядят почти также абсурдно, как попытка кинуть мячик быстрее скорости света. Насколько я знаю, CPT-инвариантность необходима для непротиворечивости Квантовой Теории Поля.
Поэтому декогеренция только выглядит как однонаправленный процесс, но на самом деле ее необратимость — термодинамическая, а не фундаментальная. И это очень важно, ведь из этого следует, что квантовая физика соблюдает CPT-инвариантность.
Насколько мы знаем, абсолютно все однонаправленные процессы в природе являются следствием второго закона термодинамики, а не фундаментальной асимметрии времени.)
Подводя итог. Декогеренция — это термодинамический процесс постоянно увеличивающейся квантовой запутанности, который удивительным образом маскируется под процесс уничтожения этой самой запутанности. Декогерентные области не взаимодействуют между собой, и каждая из них становится менее запутанной. Декогеренция — третья причина «классической галлюцинации». Она позволяет физикам рассматривать каждую область как независимую, не учитывая мизерную вероятность их взаимодействия. Кроме того, каждая отдельная область становится внутри более простой для понимания. Это очень кстати, если вы хотите решать задачи в терминах простой классической физики. И очень некстати, если вы хотите разложить на множители миллионозначное число, до того как погаснет Солнце.


