Законодательные инициативы, особенно в США, частенько становились предметом неудержимых споров и искреннего непонимания. Вот и сегодня хочу рассказать вам о билле 246 — правовом акте, который рассматривался в сенате штата Индиана в 1897 году.
Тремя годами ранее сельский врач Эдвард Гудвин (1825-1902), считавший себя неплохим математиком, опубликовал в журнале «American mathematical monthly» статью, в которой утверждал, что решил задачу квадратуры круга.
Решить задачу о квадратуре круга — значит построить циркулем и линейкой квадрат равной с кругом площади . В XIX веке было доказано, что построение циркулем и линейкой возможно, если оно сводится к алгебраическому уравнению, корни которого выражаются максимум через квадратные радикалы. Для квадратуры круга необходимо было найти уравнение, корнем которого являлось бы число π или любая его комбинация с квадратными корнями, умножением и т.д. В 1882 году немецкий математик Фердинанд фон Линдеман доказал, что π не может быть корнем никакого алгебраического уравнения тривиальные варианты не в счёт) и является трансцендентным числом, а значит, решение задачи квадратуры круга теоретически невозможно.
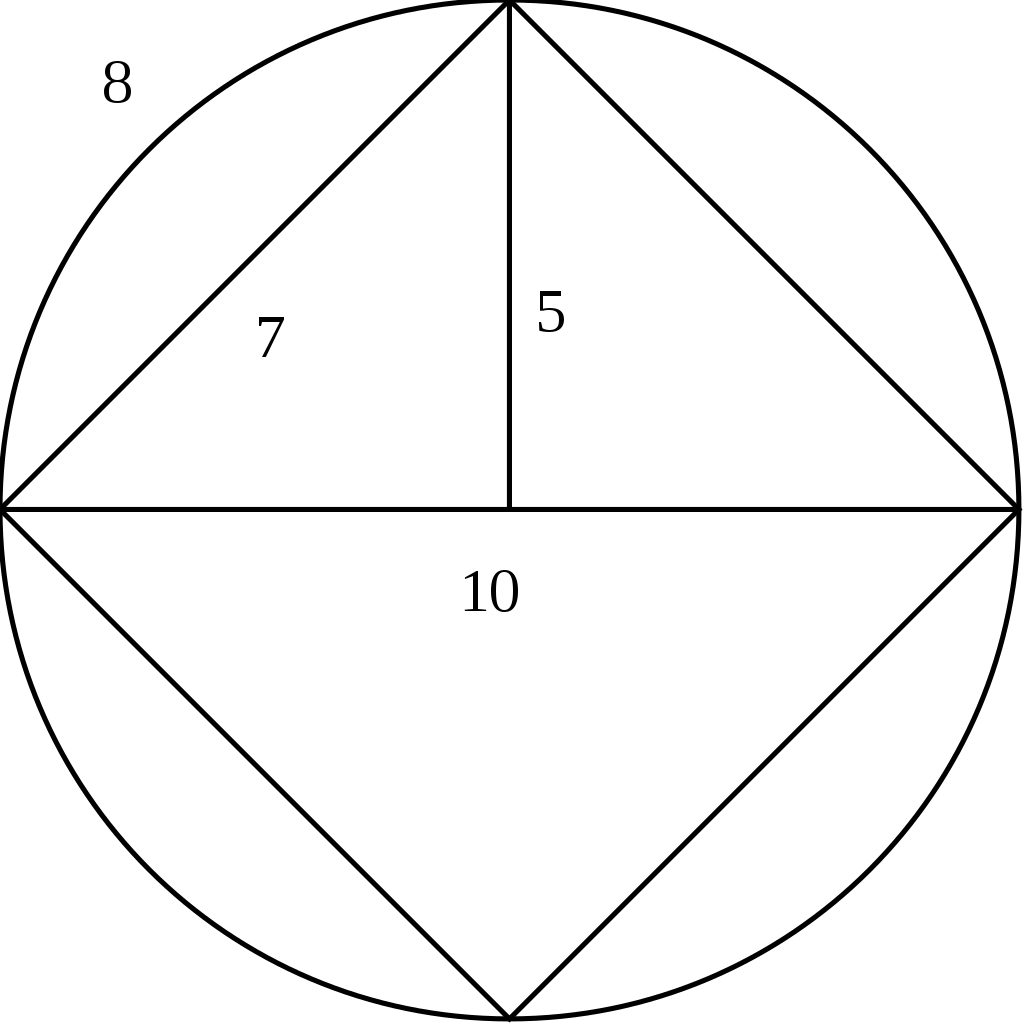
Рисунок по статье Гудвина, опубликованной в разделе «Заметки и вопросы», предполагавшей отказ от ответственности со стороны редакции журнала. Это первое оправдание публикации такого откровенного бреда. Второе в том, что на современном языке журнал пытался «хайпануть». Кстати, сам Эдвард был уверен. что решил также и две другие великие задачи древности — трисекцию угла и удвоение куба. Ну что тут сказать, главное — поверить в себя.
Главная ошибка находится прямо в начале статьи: Эдвард утверждает, что площадь круга равна площади квадрата с тем же периметром, что неверно.
Например, если взять в качестве стороны квадрата число π, его периметр равен P=4π , S = π^2, что для окружности такой же длины даёт S = 4π! Какое совпадение! За него и цепляется наш герой.
В статье утверждается, что доказано соотношение длины дуги и хорды, стягивающей угол, как 8/7 и (внимание!) соотношение диагонали квадрата и его стороны как 10/7. По этому поводу возникает вопрос: знаком ли был автор с теоремой Пифагора? Но самое удивительное, что в приведенном Гудвином в качестве доказательства чертеже фигурирует значение π = 3,2 (четыре хорды по 8 дюймов разделить на диаметр в 10 дюймов).
Интересно, что в других работах Гудвина встречались еще более удивительные значения фундаментальной константы, включая 4, 3.2325… и даже 9.2376, которое, вероятно, является «самым большим завышением π в истории математики».
Понять, как проистекал этот, без сомнения, творческий ручей, у современников не было желания, да и смысла, ведь сам Эдвард утверждал, что у него на этот счёт было божественное провидение.
И ладно бы на этом всё закончилось, ведь сколько живет математика, столько есть люди с «революционными» идеями. Однако Эдвард пошел дальше. 18 января 1897 года Гудвин убедил одного из членов Палаты представителей штата внести на рассмотрение законопроект, который установил бы его метод квадратуры круга частью свода законов штата Индиана.
Билль 246 предусматривал, в частности, авторские отчисления за «новую математическую истину и вклад в образование» в случае использования нового значения π в других штатах. Для родной Индианы, впрочем, великодушный гений налог не предусмотрел.

Оригинальный текст билля 246. В третьей секции используется классический приём «Argumentum ad verecundiam» — апелляции к авторитету. Речь идёт о том, что «неужели государевы мужи смеют противоречить рецензентам «Американского математического ежемесячника»?
И лёд тронулся. Газеты штата стали выпускать материалы о законопроекте и его авторе, называя его выдающимся математиком и сравнивая то с Ньютоном, то с Галилеем. Единственной газетой, которая пыталась донести до читателей, что задача квадратуры круга неразрешима, была Der Tagliche Telegraph, вот только выходила она на немецком языке, поэтому её публикации в штате Индиана прошли незамеченными.
Получив поддержку со стороны прессы, билль 246 успешно прошел отбор Комитета по образованию штата, получив 67 голосов из 67 возможных. Следующим этапом было рассмотрение в Сенате. Казалось бы, победа доктора Гудвина близка.
Все изменилось, когда про билль 246 узнал президент Академии наук штата Индиана и одновременно ведущий профессор математики Университета Пердью Кларенс Абиатар Уолдо.

В своих воспоминаниях Уолдо рассказал, что присутствовал при чтении законопроекта. Его даже пытались познакомить с Гудвиным, на что математик ответил, что «и так знаком со столькими сумасшедшими, что новых ему не нужно».
Чтение закончилось тем, что сенаторы отправили билль 246 на еще одно слушание в Комитет по трезвости (Committee on Temperance — именно так), откуда он вернулся с окончательной рекомендацией к принятию. К тому времени над индианапольскими законодателями потешались как внутри, так и далеко за пределами штата.

Например, местный сенатор Оррин Хаббелл объявил законопроект «полнейшей глупостью» и предложил Сенату «с таким же успехом попытаться законодательно разрешить воде бежать вверх по холму».
В конце концов под давлением общественности и усилиями профессора Уолдо Палата представителей отменила законопроект. Примечательно, что, хотя и большинство сенаторов проголосовало «против», ни у кого не возникло и сомнения, что с предлагаемой теорией может быть что-то не так, никто так и не задумался над очевидной бредовостью теории чокнутого доктора, ведь все его прекрасно знали, да и разве рецензенты серьезного журнала могут быть не правы? Билль 246 просто признали неподлежащим законодательному регулированию.
Доктор Гудвин же умер в 1902 году, но никогда не терял надежду, что его теория будет принята. Знаете, его даже немного жаль. Но это не меняет того факта, что число π = 3,14159…

