Какого цвета атомы?

16.03.2023

В этой статье мы обсудим какие бывают цветовые схемы для атомов, дальтонизм, цветовую модель RGB в контексте Python-а. А в конце мы попробуем сделать собственную цветовую схему для атомов первого и второго периодов таблицы Менделеева, исходя из того, чтобы цвета были чуточку более дружелюбнее к дальтоникам.

И да, это кликбейтный заголовок 🙂

Введение

Конечно, у атомов как у таковых цвета нет и быть не может, поскольку они излучают свет только в возбуждённом состоянии, и в зависимости от этого состояния, длина волны излучения будет разной. В качестве примера можно взять атом водорода. В видимой области электромагнитного спектра (400-750 nm), у него видны только четыре полосы из спектральной серии Бальмера.

Какого цвета атомы? — Рисунок 1. Серия Бальмера для атома водорода в видимом диапазоне

И что из этих цветов, спрашивается, считать цветом водорода?! И так для каждого из элементов…

Но тем не менее, «цвет атома» это не бессмысленное понятие. Дело в том, что мы постоянно используем модели молекул, где обозначаем атомы шариками, а химические связи между ними при помощи палочек. И чтобы пользователям было как можно удобнее распознавать где какой атом, эти самые изображают разного размера и разного цвета: каждый элемент своего размера и своего цвета. Про размеры мы говорить не будем, это отдельная и сложная тема (те кому интересно, могут прогуляться по соответствующим статьям в Википедии). А вот про цветовые схемы для разных элементов мы поговорим.

Первая полноценная пространственная молекулярная модель (ещё до появления компьютеров), была создана Робертом Кори и Лайнусом Полингом (тем самым, дважды нобелевским лауреатом, и создателем эпидемии продажи витамина C по всему миру). Они как раз тогда работали вместе над вторичной структурой белков, и такие модели им были очень полезны в их работе. В своей статье 1953 года [Rev. Sci. Instr. (1953), 24, 621] они только описали принципы своего конструктора, из которого можно было делать приближённые к реальности модельки аминокислот и полипептидов. Атомов для белков в первом приближении много не надо, поэтому там были описаны только углерод (C), азот (N), кислород (O) и водород (H). Цветовой схемы там дано не было, но по-видимому, она существовала (по-крайней мере об этом говорит Википедия).

Через несколько лет после этого, Вальтер Колтун запатентовал расширенную и более детализованную молекулярную модель [US3170246A], основываясь на работе Кори и Полинга. Позже, Колтун описал получившуюся модель в отдельной статье [Biopolymers (1965), 3, 665-679], в ней же даётся название CPK (Corey-Pauling-Koltun), по фамилиям создателей. И вот в этом патенте 1962-го и статье 1965-го даётся цветовая схема для покраски атомов, которая и войдёт в обиход как схема CPK. Собственно вот она.

Водород (H) в этой схеме предполагался белым. Видимо… потому что его не видно?
Углерод (C) — чёрным. Наверное, чтобы быть похожим на уголь или графит?
Азот (N) должен был быть синим. Без понятия почему.
Кислород (O) должен быть красным, тоже не знаю почему (кстати, жидкий кислород имеет светло-голубой цвет).
Фтор (F) должен был быть бледно-зелёным. Ну, в целом похоже на цвет жидкого и газообразного F₂.
Фосфор (P) в патенте был пурпурным, но в более поздней статье он стал бледно-жёлтым. Такое изменение, по-ходу, было сделано, чтобы сделать его похожим на белый фосфор (состоящий из молекул P₄), который в неочищенном состоянии ещё называют жёлтым фосфором.
Сера (S) там была жёлтая. Тут тоже всё ясно, самородная сера вполне себе жёлтая.
Хлор (Cl) зелёный, что, впрочем тоже хоть как-то согласуется с жёлто-зелёным цветом газа Cl₂.
Бром (Br) в патенте предполагался средне-тёмно зелёным, но в более поздней статье стал коричневым, что тоже хоть как-то похоже на красно-бурый цвет его жидкости и паров.
Йод (I) в патенте был замыкающим в зелёной семье галогенов, и предполагался тёмно-зелёным, но в статье внезапно стал фиолетовым, видимо, чтобы ассоциироваться со своими кристаллами и парами.
Металлы, типа железа (Fe), кобальта (Co), никеля (Ni) и меди (Cu), необходимые для всяких хелатов, должны были быть серебристыми шариками. Тоже вполне себе логично, хоть медь и выбивается из этого ряда своим красноватым цветом.

Вот эту чётко прописанную схему можно и считать за точку отсчёта цветовых схем атомов. И что забавно, эти самые CPK-модельки до сих пор производятся (и используются!).

Рисунок 2. CPK модельки в реале, 2023 год.

Тем не менее, жизнь не стояла на месте, с 60-х годов у нас появились компьютеры с графикой, вычислительная химия (расчёт свойств атомов и молекул при помощи квантовой механики и компьютеров) дошла до больших систем, а таблица Менделеева к 2016 году официально разрослась до 118 элементов. И отсюда очевидно, что великолепия CPK-схемы давно перестало хватать для повседневной жизни. Поэтому появился зоопарк различных схем раскраски атомов. Для примера давайте возьмём простую молекулу, 2-хлор-1,1-дифторэтилен (не пугаемся названия!), скачаем файл со структурой с сайта NIST Chemistry WebBook, и откроем его в шести разных молекулярных визуализаторах: Avogadro, Chemcraft, UCSF Chimera, Jmol, Molden и RasMol. В результате получим следующий зоопарк разноцветных попугаев:

Рисунок 3. 2-хлор-1,1-дифторэтилен в разных визуализаторах.

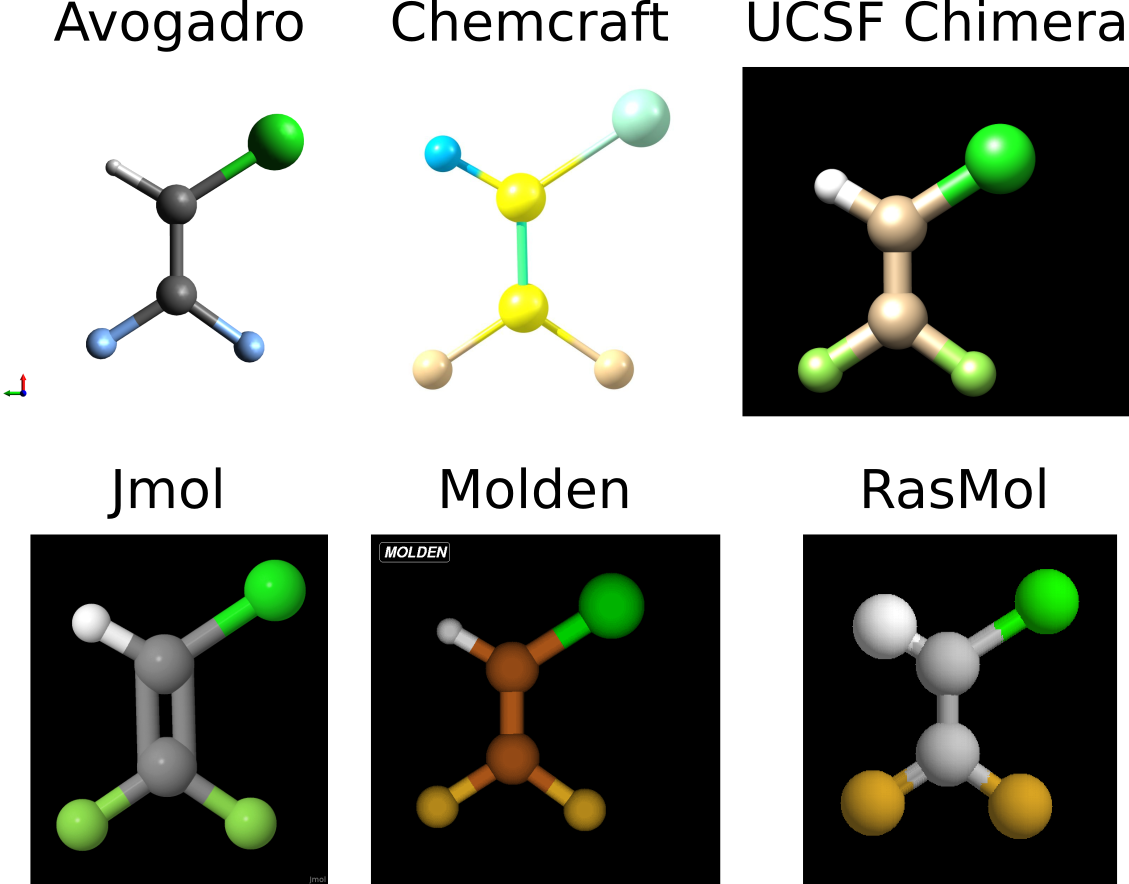
Без подписей и озарения свыше не поймёшь где какой атом, и классическая CPK-схема, где каждый из четырёх типов атомов этой молекулы (H, C, F, Cl) присутствует, поможет нам только в случае Jmol-а. Собственно, цветовая схема этого визуализатора и является наиболее прямой наследницей CPK, но не без изменений (например, углерод вместо чёрного стал серым). Само собой, при разработке всех этих цветовых гамм, никак не учитывалось, что некоторые люди, которые будут на эти молекулы смотреть, являются дальтониками. Поэтому, в этом посте мы попробуем разобраться с дальтонизмом, основами цветовой модели RGB и питоновской библиотекой Pillow, и даже попробуем получить свою собственную цветовую схему для атомов. Поехали!

Дальтонизм, или цветовая слепота

Собственно, вопрос состоит в том: как именно мы видим? Не пускаясь во всякие сложности, типа цис-транс изомеризации ретиналя под действием излучения, остановимся на простой модели. В наших глазах ~~звёздная ночь~~ есть два вида фоторецепторов: палочки (по-английски это «rods», стержни) и колбочки (или «cones», конусы). Палочки очень высокочувствительны к свету, поэтому работают даже когда света очень мало, т.е. в темноте. Но при этом палочки чувствительны только к одному диапазону длин волн света, поэтому они дают чёрно-белое зрение (много или мало света). Максимум поглощения палочек (498 нм) соответствует изумрудно-зелёному.

А вот колбочки как раз чувствительны к длине волны света, но как результат, им требуется гораздо больше света, чтобы работать, поэтому в темноте они практически не работают. Из-за этого в сумерках мы видим всё чёрно-белым. Колбочек в глазах у нас три вида, и они отвечают за то, что мы можем видеть три цвета: синий, зелёный и красный, для краткости будем их обозначать буквами «B», «G» и «R», соответственно.

Синие колбочки (B), отвечают за поглощение коротковолнового излучения, с максимумом на 420 нм.
Зелёные колбочки (G), с максимум поглощения на 534 нм, для средних волн.
Красные колбочки (R), для длинных волн, максимум на 564 нм.

Рисунок 4. Спектры поглощения фоторецепторов глаза и спектр испускания Солнца, аппроксимированный по формуле излучения чёрного тела для температуры 5778 K.

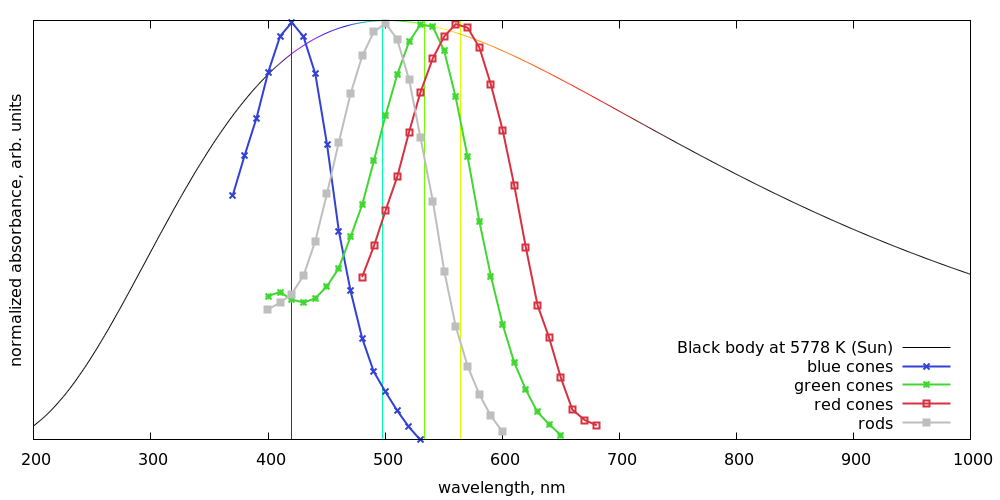
Спектры поглощения (вероятность поглощения фотона каждой конкретной длиной волны) этих фоторецепторов, взятые из статьи [J. Physiol. (1980), 298, 501-511], даны на рисунке выше. Если сравнить их со спектром яркости нашей любимой звезды, по имени Солнце, который вполне себе описывается законом Планка для температуры в 5778 K, то оказывается, что все они лежат в районе максимума испускания. Эволюция, однако.

И что же такое цветовая слепота, или дальтонизм? Это, собственно, генетически-обусловленная или (реже) приобретённая проблема в работе этих самых колбочек, отвечающих за цветовое восприятие. Если повредить один или несколько фоторецепторов из трёх, восприятие цветов будет или не такое чёткое, или вообще будет отсутствовать. Есть два варианта повреждения колбочек. Первое – это полное отсутствие колбочек какого-то типа (R, G, B), такое повреждение мы будем обозначать зачёркнутым текстом, например, R. Второе, менее жёсткое повреждение – это наличие вместо одной из нормальной колбочек, аналогичной ей аномальной (где активность пигмента снижена). Эти аномальные колбочки мы будем обозначать маленькими буквами r, g, b, для красной, зелёной и синей колбочек соответственно. В зависимости от того, что именно и насколько именно повреждено, существуют следующие типы цветового восприятия.

Рисунок 5. Варианты дальтонизма и примерная иллюстрация восприятия изображения в верхнем левом углу у людей, с данной особенностью.

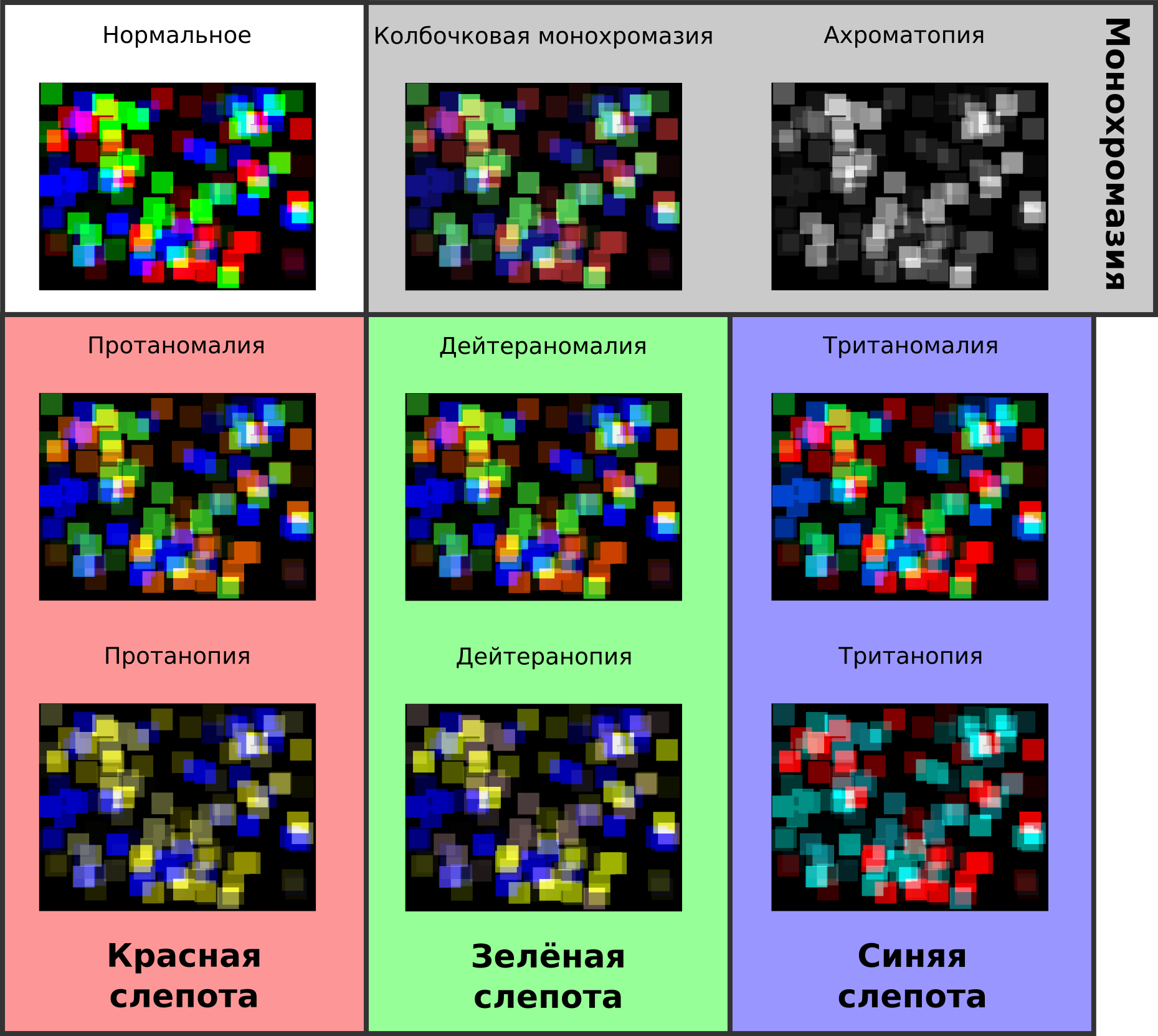
Первое это, само собой, нормальное зрение, когда в глазу есть все три вида колбочек, и все нормального типа, т.е. RGB.
Если ломается/меняется только один из видов цветовых рецепторов, то наступает т.н. частичная цветовая слепота. И здесь есть три варианта мягкого развития событий: замена красных рецепторов с нормальных на аномальные (rGB) приводит к протаномалии, зелёных (RgB) – к дейтераномалии, а синих (RGb) – к тританомалии. В жёстком случае, когда вместо ослабевания работы рецептора имеется полное его отсутствие, получаются три аналогичные ситуации: отсутствие красного (RGB) приводит к протанопии, зелёного (RGB) – к дейтеранопии, а синего (RGB) – к тританопии.
Ну и в конце идёт самый жёсткий вариант цветовой слепоты: монохромазия, полное отсутствие цветового зрения. И на самом деле тут два подварианта разной степени жёсткости: ахроматопия, когда нет ни одного цветового рецептора (~~RGB~~), или колбочковая монохромазия, когда в наличие всё же есть один вид колбочек. В последнем случае, чаще всего это синие (RGB), реже зелёные (RGB) и совсем редко, в наличие остаются только красные (RGB).

Примерная иллюстрация всех этих типов восприятия дана на картинке выше, и в сейчас мы перейдём к обсуждению того, как эти картинки были получены.

Цвета на подушке

Собственно, чтобы обсуждать цвета и цветовые схемы, особенно в контексте изображений на компьютере, нам нужна цветовая модель. В качестве таковой, давайте возьмём самую простейшую, RGB. Несмотря на все её несовершенства, она является наиболее простой и удобной в работе, что очень нам поможет на следующей стадии создания своей цветовой схемы для атомов. Итак, базовая идея идея аддитивной цветовой модели RGB следующая (внимание и на рисунок ниже).

Рисунок 6. Общая схема сборки RGB изображения из отдельных красной (R), зелёной (G) и синей (B) компонент.

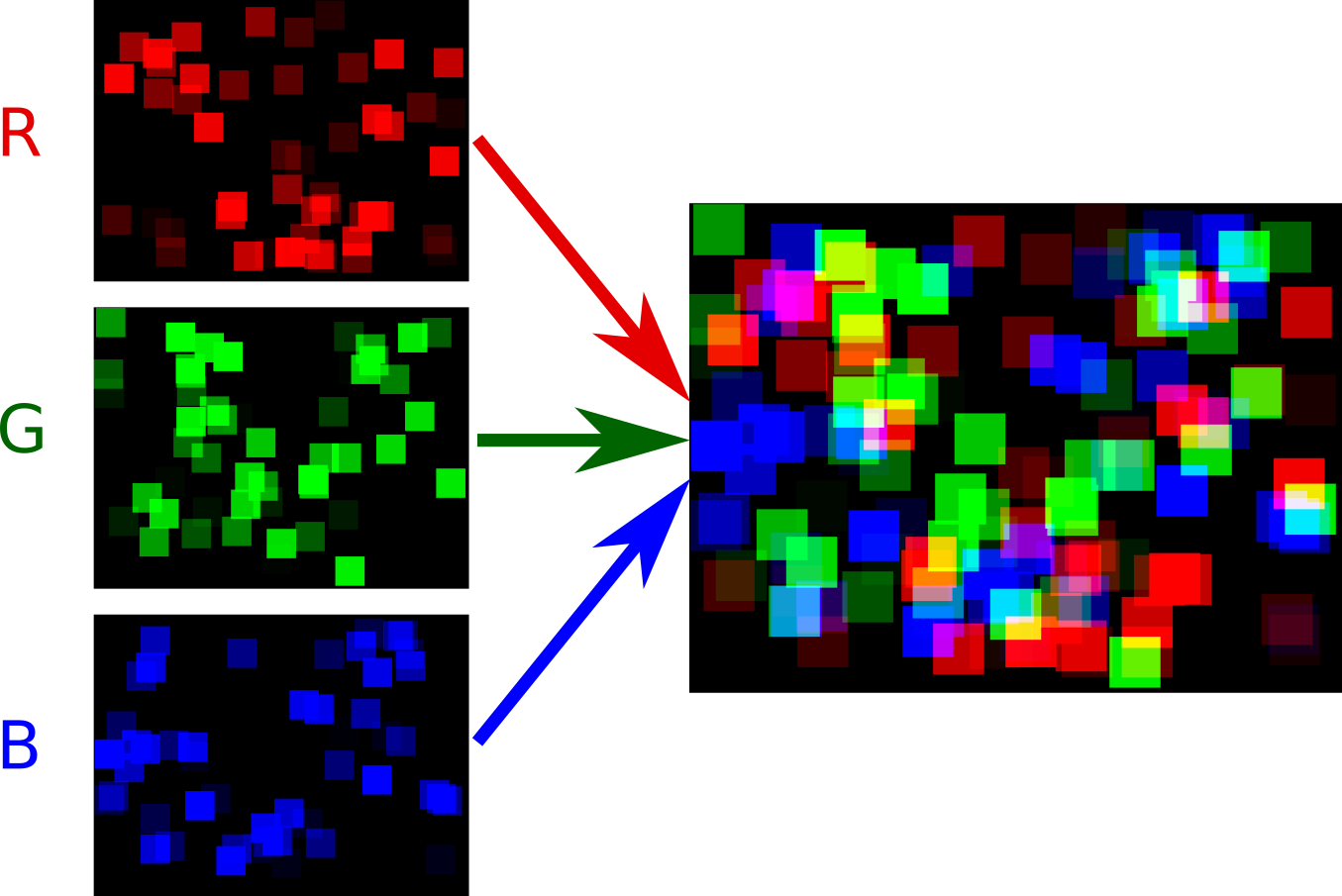
Каждый цвет мы будем представлять как три числа: R, G, B, которые обозначают количества красного, зелёного и синего цветов, соответственно. Каждое из этих значений даётся в виде неотрицательного восьмибитного целого числа (uint8), и соответственно R, G и B могут принимать значения от 0 (нет цвета) до 2⁸-1=255 (максимальная интенсивность данного цвета). Соответственно, максимально яркий чистый красный мы получим если R=255, G=0, B=0, зелёный, если R=0, G=255, B=0, и синий в случае R=0, G=0, B=255. Если мы одновременно выключим каждый цвет (R=0, G=0, B=0), то наступит тьма, ~~мрак и печаль,~~ и цвет чёрный получим мы. Если же, наоборот, выкрутить интенсивность каждого из цветов на максимум (R=255, G=255, B=255), то получим мы цвет абсолютного света, то бишь белый.

Если посмотреть на эту цветовую модель с точки зрения линейной алгебры, то станет очевидно, что у нас имеется куб в трёхмерном (x,y,z) пространстве со стороной от 0 до 255 по каждой из трёх осей. Оси (или базисные вектора) у нас – это цвета: x=R, y=G, z=B, поэтому каждый наш цвет мы можем легко представить в виде трёхмерного вектора C=(R,G,B). Это представление не добавляет ничего нового к модели RGB, но позволяет упростить запись некоторых операций, чем мы воспользуемся далее.

Цвета мы закодировали в рамках нашей модели, но как же получить изображение? Допустим у нас картинка размером N_v на N_h пикселей, где первое число показывает число пикселей по вертикали (v) а второе – по горизонтали (h). Все эти N_v×N_h пикселей можно разместить в виде двумерного массива, скажем в виде NumPy-евского с формой (N_v,N_h ). Если каждый пиксель (элемент массива) будет принимать значения от 0 до 255, то это можно проинтерпретировать как чёрно-белое изображение, где 0 соответствует чёрному, 255 – белому, а остальные значения – 254 оттенкам серого.

Для примера, возьмём вселюбимый Python. Нагенерить матрицу (псевдо)рандомных чисел в искомом дипапзоне значений мы можем, например при помощи numpy.random.randint следующим образом:

import numpy as np
Arr = np.random.randint(low=0,high=255, size=(Nv,Nh))

И чтобы построить изображение, мы можем воспользоваться питноновской библиотекой Pillow. Когда-то в древние времена существовал Python Imaging Library (PIL), и когда его поддержка прекратилась, его форкнули, и продолжили разработку под милым названием «подушка» (pillow). Подключить нужный нам модуль Image из этой библиотеки легко, достаточно добавить в код: from PIL import Image. Чтобы создать чёрно-белую картинку этим самым Image из созданного выше массива Arr, достаточно написать следующий код:

Arr = np.array(Arr, dtype=np.uint8)
img = Image.fromarray(Arr)
img.save('simple_bw_image.png')

Первая команда важна: Image требует формат данных uint8, обычный int его не устраивает. Посему, это и добавляем. В результате, мы получим нечто похожее на экран старого ненастроенного телевизора:

Рисунок 7. Пример нашего чёрно-белого изображения.

Но модульImage может дать нам и цветное изображение, надо только предоставить ему три матрицы: для красного (R), зелёного (G) и синего (B) цветов. Допустим, мы их сгенерили тем же способом, что и Arr, тогда нам остаётся их состыковать в единый трёхмерный массив размера (Nv,Nh,3), где последний индекс идёт от 0 до 2 и нумерует, соответственно R, G, B матрицы (цветовые компоненты RGB-изображения). Чтобы состыковать их, можно воспользоваться процедурой numpy.dstack. В результате чего RGB-изображение можно построить следующими командами:

rgb = np.array(np.dstack((R,G,B)),dtype=np.uint8)
img = Image.fromarray(rgb)
img.save('simple_rgb_image.png')

На выходе мы получим уже простое изображение ненастроенного чуть более нового, цветного телика:

Рисунок 8. Пример нашего цветного RGB-изображения

Полный код генерации этих картинок спрятан под спойлером ниже.

Полный код тута

import numpy as np    
from PIL import Image # для изображений

# Число пикселей по вертикали и горизонтали изображения
Nv = 480
Nh = 640

# построим простое чёрно-белое изображение
# для начала, нагенерим случайный двумерный массив (Arr) чисел от 0 до 255
Arr = np.random.randint(low=0,high=255, size=(Nv,Nh))
# потом этот массив переведём в тип uint8
Arr = np.array(Arr, dtype=np.uint8)
# создадим изображение при помощи модуля Pillow
img = Image.fromarray(Arr)
# ну и сохраним это изображение в виде PNG-файла
img.save('simple_bw_image.png')

#Та-Да!

# А теперь проделаем то же самое для цветного RGB-изображения
# Сделаем (аналогично Arr выше) красную (R) часть изображения
R = np.random.randint(low=0,high=255, size=(Nv,Nh))
# Теперь сделаем (аналогично Arr выше) зелёную (G) часть изображения
G = np.random.randint(low=0,high=255, size=(Nv,Nh))
# И наконец, сделаем синюю (B) часть изображения
B = np.random.randint(low=0,high=255, size=(Nv,Nh))
# теперь соберём их в массив формы (Nv,Nh,3), состыкавав три наши матрицы
# ... и заодно сразу переведём числа в uint8
rgb = np.array(np.dstack((R,G,B)),dtype=np.uint8)
img = Image.fromarray(rgb)
img.save('simple_rgb_image.png')

Отлично, изображения мы делать научились, а как же имитировать разные варианты дальтонизма? Как видно из Рисунка 4 (спектров поглощения фоторецепторов), если выключить один из рецепторов, нужно будет считать получившийся спектр восприятия против спектра освещённости (поскольку чувствительности фоторецепторов в некоторых диапазонах перекрываются), короче, кошмар. По счастью, ~~всё украдено до нас~~ некоторые умные люди из этих наших Интернетов, уже подумали над этой проблемой, и запараметризовали всё это в виде простой матричной модели. Поскольку наша RGB модель это трёхмерное векторное пространство, нам удобно записать преобразование цветов (векторов) в виде трёхмерных матриц. В результате параметризации, например, матрица для имитации ахроматопии выглядит как

$\mathcal{M} = \begin{pmatrix} 0.299 & 0.587 & 0.114 \\ 0.299 & 0.587 & 0.114 \\0.299 & 0.587 & 0.114 \\\end{pmatrix}$

Для нормального зрения, понятное дело, M – это единичная матрица. Собственно, действуя на каждый трёхмерный RGB-пиксель изображения матрицей при помощи NumPy-евской команды матричного умножения (numpy.matmul), и были получены все изображения восприятия разных типов дальтонизма на Рисунке 4. Сами же матрицы (для экономии места) убраны под спойлер ниже.

А здесь даны все нужные нам девять матриц в виде NumPy-евских массивов

#Copy the matrixes from https://gist.github.com/Lokno/df7c3bfdc9ad32558bb7

AllMat = dict()

# normal vision
MT = np.array([[1,0,0],
               [0,1,0],
               [0,0,1]])
AllMat.update({"normal": MT})

# Red-Blind
MT = np.array([[0.567,0.433,0.000],
               [0.558,0.442,0.000],
               [0.000,0.242,0.758]])
AllMat.update({"protanopia": MT})

# Red-Weak
MT = np.array([[0.817,0.183,0.000],
               [0.333,0.667,0.000],
               [0.000,0.125,0.875]])
AllMat.update({"protanomaly": MT})

# Green-Blind
MT = np.array([[0.625,0.375,0.000],
               [0.700,0.300,0.000],
               [0.000,0.300,0.700]])
AllMat.update({"deuteranopia": MT})

# Green-Weak
MT = np.array([[0.800,0.200,0.000],
               [0.258,0.742,0.000],
               [0.000,0.142,0.858]])
AllMat.update({"deuteranomaly": MT})

# Blue-Blind
MT = np.array([[0.950,0.050,0.000],
               [0.000,0.433,0.567],
               [0.000,0.475,0.525]])
AllMat.update({"tritanopia": MT})

# Blue-Weak
MT = np.array([[0.967,0.033,0.00],
               [0.00,0.733,0.267],
               [0.00,0.183,0.817]])
AllMat.update({"tritanomaly": MT})

# Monochromacy
MT = np.array([[0.299,0.587,0.114],
               [0.299,0.587,0.114],
               [0.299,0.587,0.114]])
AllMat.update({"achromatopsia": MT})

# Blue Cone Monochromacy
MT = np.array([[0.618,0.320,0.062],
               [0.163,0.775,0.062],
               [0.163,0.320,0.516]])
AllMat.update({"achromatomaly": MT})

Делаем цветовую схему

Ну и коль скоро мы разобрались с цветовым представлением изображений, мы можем наконец перейти к оптимизации нашей собственный цветовой схемы раскраски атомов! А то небось уже забыли о чём эта статья вообще…

Итак, какой должна быть идеальная схема покраски атомов? Как по мне, она должна удовлетворять трём требованиям.

Цвета атомов должны быть максимально контрастны для всех видов цветового восприятия. Т.е. если два атома встретятся рядом, не важно, хорошее ли у нас зрение, или монохромазия, мы с большой вероятностью должны заметить эту разницу в цветах. Естественно, стоит учесть, что увидеть рядом на картинке в научной статье какой-нибудь оганесон (Og) и кремний (Si) у нас не очень много шансов, поэтому стоит как-то учесть и вероятности найти конкретные элементы вообще, и вероятность встретить конкретную пару рядом.
У нас обычно имеется какой-то фон наших картинок, поэтому чисто цвета атомов должны ещё контрастировать с цветом этого фона. Чаще всего это или чёрный или белый задник (см. Рисунок 3).
Ну и не очень обязательный пункт: цвета должны быть похожи на какую-то из классических цветовых решений для атомов. Можно, конечно, как футуристы, отвергнуть всё старое, чтобы строить новое, но я не настолько радикален.

Попробуем это всё учесть. Начнём с того, что посмотрим, на какие из элементов при создании цветовой схемы нам надо больше обращать внимание. Для этого нам бы нужна какая-то база данных химических соединений, типа PubChem-а или ChemSpider-а. Но, как оттуда достать все их миллионы соединений за раз (их брутто-формулы) я не понял. Поэтому пришлось обратиться к чуть менее обширной, но более открытой NIST Chemistry WebBook. Оттуда (здесь) можно скачать список всех соединений, что у них есть. Распарсив все формулы при помощи удобного модуля chemparse, мы можем построить количество соединений в базе данных на 72618 соединений:

Рисунок 9. Количество соединений, содержащих выбранные химические элементы в базе данных NIST Chemistry WebBook.

Как видно, в основном в базе данных NIST Chemistry WebBook содержатся органические молекулы, поэтому подавляющее число соединений содержат водород (H), углерод (C), ну и сопутствующие им кислород (O) и азот (N). Чтобы узнать, какие из элементов встречаются чаще или реже в парах, можно использовать пирсоновский коэффициент корреляции (ρ), который (грубо говоря!) равен +1, если два события все время происходят вместе, -1, если одно исключает другое, и 0, если между двумя событиями нет особо никакой корреляции. Получившаяся матрица корреляции для всех элементов для наших данных дана ниже:

Рисунок 10. Корреляция между различными элементами в соединениях из базы данных NIST Chemistry WebBook.

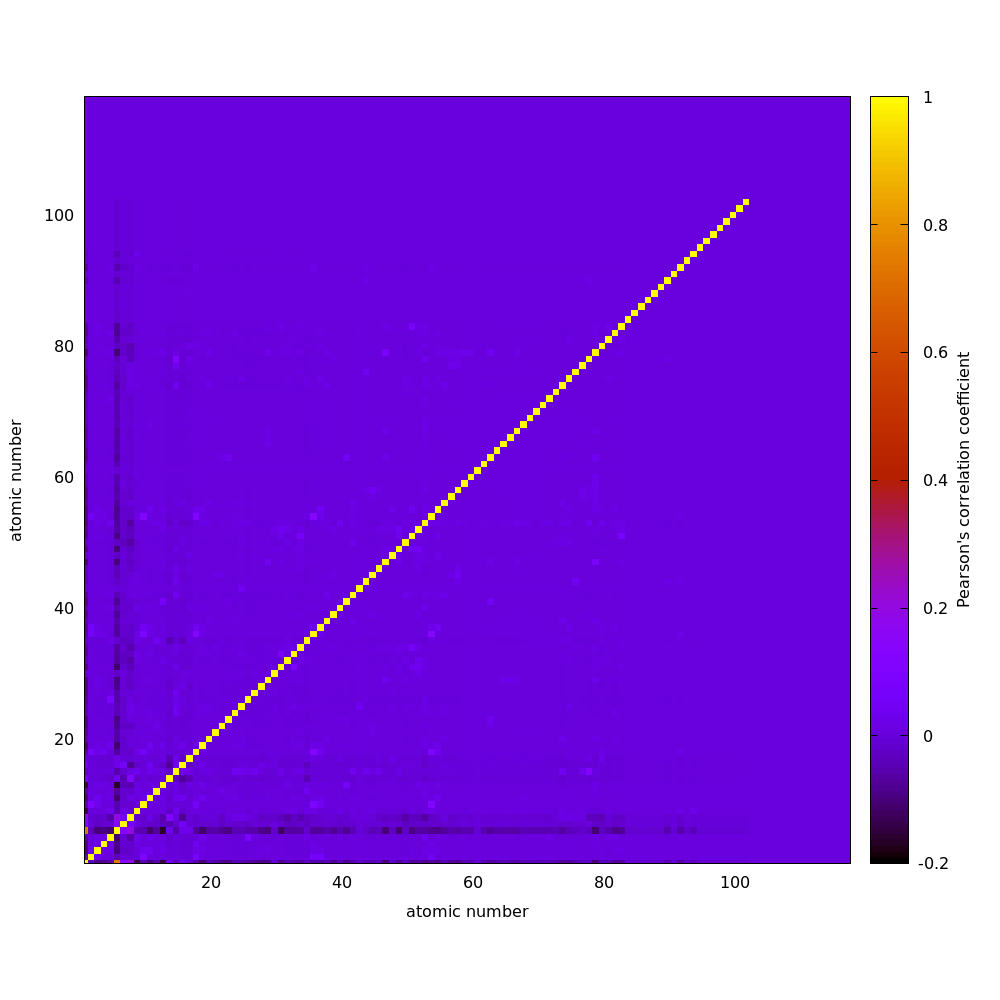
На диагональ можно не смотреть, там понятно единицы, но и вне диагонали полно корреляций. Понятно, что углерод (атомный номер Z=6) коррелирует с водородом (атомный номер Z=1) с корреляцией ρ(1,6)=0.8, раз база данных в основном состоит из органики. Были и неожиданные корреляции, например для платины (Z=78) c фосфором (Z=15) ρ(78,15)=0.1. Но были и антикорреляции, например для водорода (Z=1) и фтора (Z=9) коэффициент ρ(1,9)=-0.1, что, впрочем, объясняется фторзамещенными соединениями, типа фреонов.

Так или иначе, мы должны желать в первую очередь оптимизировать схему так, чтобы:

раздвигать друг от друга дальше в пространстве RGB те атомы, что чаще встречаются,
раздвигать друг от друга сильнее те, что чаще встречаются вместе, а о тех, что встречаются редко вместе, или вообще не очень друг друга любят, не париться не так сильно.

Нам нужно охарактеризовать расстояние (D) между RGB-цветами C_i=(R_i,G_i,B_i) и C_j=(R_j,G_j,B_j) для атомов номер i и j, которые меняются от i,j=1 (водород) до i,j=Z_max, где Z_max это номер последнего элемента, который мы включаем в рассмотрение (2≤Z_max≤118). Для нашей цели мы можем использовать обычное эвклидово (теоремно-пифагорное) расстояние в трёхмерном пространстве RGB:

$D_{ij} = \sqrt{(\mathbf{C}_i - \mathbf{C}_j)^2 } = \sqrt{(R_i - R_j)^2 + (G_i - G_j)^2 + (B_i - B_j)^2}$

В случае нормального зрения это вполне себе нормальная оценка (не лучшая, но всё же). А что же делать в случае, если у нас есть искажение цветового восприятия.

Допустим, что наш вид дальтонизма описывается матрицей M, тогда под её действием любой цвет C=(R,G,B) переходит в c=MC. Соответственно, разность векторов c_i=MC_i и c_j=MC_j будет равна (c_i—c_j)=(MC_i—MC_j)=M(C_i—C_j). А значит расстояние (d) в метрике RGB для преобразованных цветов c_i и c_j будет равн.

$d_{ij} = \sqrt{(\mathbf{C}_i - \mathbf{C}_j)^\mathrm{T} \mathcal{M}^\mathrm{T} \mathcal{M} (\mathbf{C}_i - \mathbf{C}_j) }$

В качестве функции, которая будет «расталкивать» пары атомов я выбрал

$\Phi_1(\mathbf{C}_1, \mathbf{C}_2, \ldots, \mathbf{C}_{Z_{\max}} ) =\sum_{k=1}^{9} \sum_{i=1}^{Z_{\max}-1} \sum_{j=1}^{i-1} \frac{w_{ij}}{d_{k,ij}^{2}}$

где k нумерует матрицы M_k для имитации восьми вариантов дальтонизма и одного нормального зрения, которые используются для расчёта разных расстояний между цветами атомов d_k, а w_ij≥0 обозначет вес конкретной пары атомов. В качестве таких неотрицательных весов можно взять следующее жуткое выражение:

$w_{ij} = \log(N_i \cdot N_j) \cdot \exp(\rho_{ij})$

где N_i и N_j обозначают количества соединений, содержащих элементы номер i и j в нашей базе данных (по-сути числа из Рисунка 9), а ρ_ij обозначает пирсоновскую корреляцию для встречи этих элементов в той же базе (элементы матрицы, показанной на Рисунке 10). Чтобы избежать логарифмирования нуля, ко всем честным числам N_i, посчитанным из NIST-а, была прибавлена двойка.

В функции Φ₁ мы делим на квадрат расстояния d_k из двух соображений: во-первых, чтобы не считать при каждом вычислении этой функции кучу корней, а во-вторых, чтобы не столкнуться с проявлениями теоремы Ирншоу. Если мы будем искать минимум функции Φ₁, относительно параметров C₁,C₂,… то мы будем как бы расталкивать цвета в RGB пространстве, причём с учётом всех вариантов особенностей цветового восприятия, с силой отталкивания заданной весами w_ij. Иными словами мы свели задачу поиска подходящей цветовой гаммы для атомов к обычной задаче минимизации.

Правда, поскольку цвет каждого атома имеет три параметра (R,G,B), то число параметров оптимизации у нас равно 3×Z_max, что для всей таблицы Менделеева (Z_max=188) означает поиск 3×118=354 параметров… очень дорого. Поэтому давайте для демонстрационных целей ограничимся первым и вторым периодом, т.е. первыми десятью элементами (Z_max=10), от водорода (H, Z=1) до неона (Ne, Z=10), включительно, т.е. всего-лишь тридцатимерной оптимизацией.

Но, как мы уже обозначили выше, одного только условия «расталкивания цветов» недостаточно, ещё нужны контраст от чёрного или белого фона и привязка к старым цветам. Их мы тоже добавим в виде функций, которые достигают минимума при выполнении наших хотелок. С чёрно-белым фоном всё просто. Расстояния цвета C_i=(R_i,G_i,B_i) атома номер i от чёрного, с координатами C_black=(0,0,0), и белого, с координатами C_white=(255,255,255), равны, соответственно

$\begin{cases} d_{k,i,\mathrm{black}} = \sqrt{(\mathbf{C}_i - \mathbf{C}_\mathrm{black})^\mathrm{T} \mathcal{M}^\mathrm{T} \mathcal{M} (\mathbf{C}_i - \mathbf{C}_\mathrm{black}) } \\ d_{k,i,\mathrm{white}} = \sqrt{(\mathbf{C}_i - \mathbf{C}_\mathrm{white})^\mathrm{T} \mathcal{M}^\mathrm{T} \mathcal{M} (\mathbf{C}_i - \mathbf{C}_\mathrm{white}) } \end{cases}$

И устраивающей нас функцией, по аналогии с Φ₁, будет

$\Phi_2(\mathbf{C}_1, \mathbf{C}_2, \ldots, \mathbf{C}_{Z_{\max}} ) =\sum_{k=1}^{9} \sum_{i=1}^{Z_{\max}} \left( \frac{1}{d_{k,i,\mathrm{black}}^{2}} + \frac{1}{d_{k,i,\mathrm{white}}^{2}} \right)$

Здесь нам взвешивать ничего не надо, поскольку, наверное, мы хотим всегда иметь хоть какой-то контраст от фона для всех атомов без исключения.

А для привязки к старым цветам можно не извращаться, а использовать обычную L₂-регуляризацию. Для каждого атома i у нас есть его дефолтный цвет X_i в какой-то из схем (здесь мы используем Jmol-овские), поэтому для привязки мы можем использовать следующую функцию:

$\Phi_3 (\mathbf{C}_1, \mathbf{C}_2, \ldots, \mathbf{C}_{Z_{\max}} ) = \sum_i \log(N_i) \cdot (\mathbf{C}_i - \mathbf{X}_i)^2$

Здесь мы всё же взвесим на частоту появления соответствующего атома, поскольку чем чаще встречается атом, тем больше к нему привыкаешь. А какой-нибудь неведомый неведомый фермий (Fm, Z=100), или даже гелий (He, Z=2) не так часто приходится видеть, поэтому и скучать по цвету, который не помнишь, вероятно будешь меньше. Ну и по разным дальтоническим схемам усреднять тоже не нужно, поскольку и так знаем цвет.

В результате для получения цветовой схемы нам нужно совершить следующую минимизацию с некоторыми произвольно-заданными весами дополнительных штрафных функций (λ₁,λ₂≥0):

$\Phi(\mathbf{C}_1, \mathbf{C}_2, \ldots, \mathbf{C}_{Z_{\max}} ) = \Phi_1 + \lambda_2 \Phi_2 + \lambda_3 \Phi_3 \rightarrow \min$

И по-хорошему эта минимизация должна быть глобальной. По счастью в SciPy в модуле scipy.optimize есть несколько алгоритмов глобальной оптимизации. Для нашего случая, я выбрал scipy.optimize.differential_evolution и значения весов λ₁=1 и λ₂=10^-7. После восьми минут оптимизации на кластере, я получил искомую цветовую схему:

Рисунок 11. Сравнение изначальной (Jmol) и оптимизированной схемы цветов для атомов двух первых периодов. В каждом ряду атомы расположены в порядке возрастания их порядковых номеров.

Невооружённым глазом видно, что больше всего изменили свои цвета редко встречающиеся гелий и неон (второй и десятый, последний, шарики), да и бериллий (четвёртый, что между бором и литием) пожелтел, но в остальном всё очень похоже на то, что и было. Поэтому чтобы охарактеризовать выигрыш в каждом конкретном (k-м) случае цветового восприятия, можно посчитать взвешенную сумму расстояний между цветами атомов:

$wS_k = \sum_{i=1}^{Z_{\max}-1} \sum_{j=1}^{i-1} w_{ij} d_{k,ij}$

Если мы это сделаем, то получим следующую картину.

Рисунок 12. Взвешенная сумма для расстояний между цветами всех пар атомов для изначальной цветовой схемы Jmol-а (initial guess), и для нашей схемы, оптимизированной по нашему алгоритму (final fit), для нормального зрения и всех видов дальтонизма.

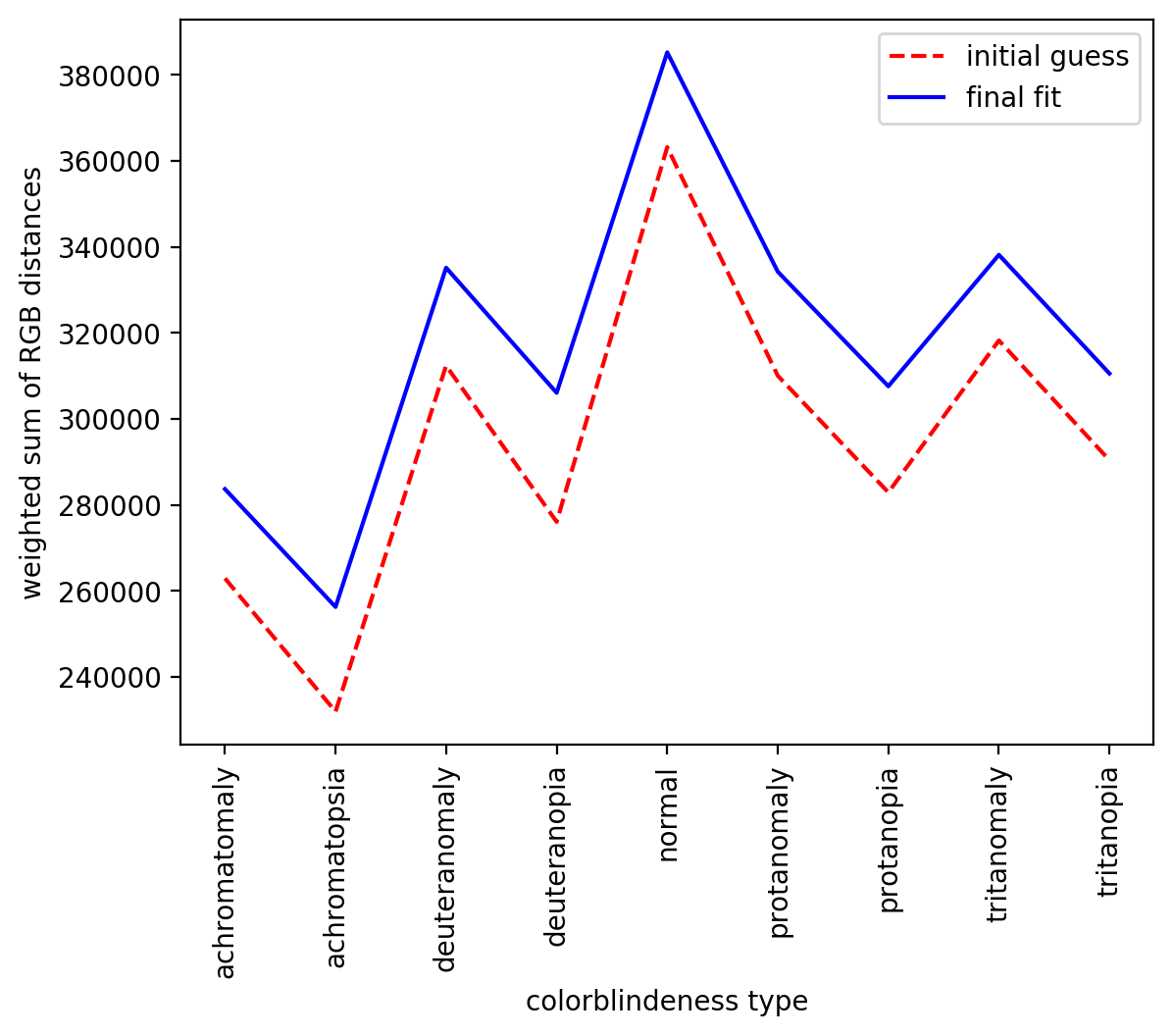
Как видно, численно, все эти суммы для каждого из отдельных случаев систематически выросли, поэтому формально мы действительно что-то улучшили. Но, конечно, это всё просто числа, но по-настоящему надо спрашивать мнения тех, для кого это делается, т.е. людей. Так что ~~давайте устроим срач~~ пишите что думаете в комментариях 🙂 Ну а для затравки, вот сравнение двух (абсолютно нереальных) молекулярных систем, построенных из всех первых десяти атомов периодической таблицы:

Рисунок 13. Сравнение старой и новой цветовой схемы на фантастической молекулярной системе.

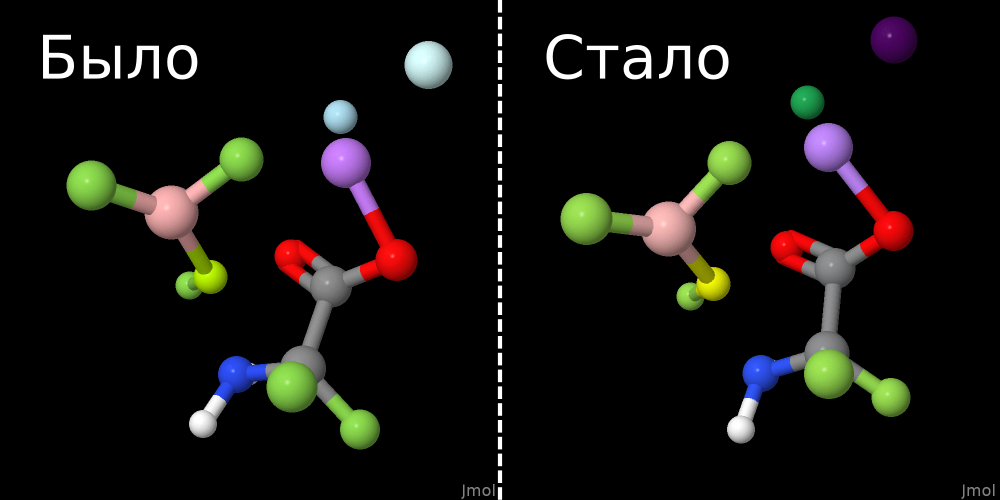
Заключение

У внимательно прочитавшего этот текст человека должен остаться вопрос: а ~~нафига~~ зачем это всё, простите, надо? Много текста, графики разные, а при этом вместо полноценной новой схемы на всю периодическую систему, какой-то пшик на десять атомов? А вот, собственно, ради этого вопроса всё и писалось.

Проблема создания палитры раскраски атомов реальна, достаточно взглянуть на цветовые решения разных визуализаторов (вновь отсылаю к Рисунку 3). У нас есть CPK схема 1950-1960-х годов на три с половиной атома плюс откуда-то возникшие её модификации. И в то же самое время с 1952-го года, когда был открыт сотый элемент (фермий, Fm), таблица Менделеева выросла на 18 элементов! При этом, по-сути, нет ни одной современной более-менее вменяемой опубликованной попытки сделать систематическую и как-то обоснованную цветовую схему для элементов. И даже Международный союз теоретической и прикладной химии (IUPAC), который регламентирует практически всё что только возможно, например такое базовое понятие как «радиан«, не имеет какой-то даже самой замшелой рекомендации по поводу цветовых решений для атомов. Так что в данном конкретном вопросе можно не переживать о ситуации, описанной в известном комиксе XKCD номер 927, у нас по-сути до сих пор нет ни одного стандарта.

И данный пост был написан с двумя целями.

привлечь внимание к проблеме,
дать конструктивное предложение по поводу возможного её решения.

Как мне кажется, адекватный способ решения проблемы следующий.

Сделать автоматическую глобальную оптимизацию цветовой схемы атомов, исходя из разумных предпосылок.
Взять фокус-группу с конкретными видами людей с разными цветовыми восприятиями и протестировать схему на них. В случае неудачного испытания, сделать выводы об ошибках, подкрутить процедуру на стадии 1 и ещё раз повторить цикл из шагов 1 и 2.
Когда наконец оптимальная схема найдена, систематически и доходчиво описать её процесс получения и её саму.
Опубликовать на всеобщее обозрение.
Happy End, но если есть силы и желание, заставить IUPAC взять результаты на вооружение в качестве стандарта.

Само собой, те конкретные принципы, что описаны здесь можно улучшить в нескольких местах. Во-первых, база данных, на которых будет основываться схема (веса элементов и прочее), должна содержать не только всякие соединения, но и кристаллы, и просто всякую выборку результатов научных статей. Во-вторых, вместо модели RGB можно использовать что-то из альтернативных вариантов: sRGB, CMYK, HSB и т.д. В-третьих, дальтонизм можно учитывать в более сложных моделях. Ну а про то, как именно делать оптимизацию, я вообще молчу, там поле непаханное: начиная от просто хорошего кода, до эффективных вычислительных алгоритмов, например, эксплуатирующих целочисленную природу цветовых моделей и более кастомовых алгоритмов глобальной оптимизации.

Так что, те, кто может улучшить мир, пожалуйста, улучшите его. Ну а тем, кто просто прочитал всё это по приколу, спасибо за прочтение :.