Как устроены волны

Волны — это самое распространённое явление. Физические колебания, звук, свет, радио и рентген, волны вероятности в квантовой механике, гравитационные волны в теории относительности — физика практически состоит из волн. Каждое явление можно изучать отдельно, но есть что-то общее в волнах, универсальное.

Чтобы ухватить это общее предлагаю разбираться в волнах последовательно.

Начнём с вопроса, на первый взгляд не связанного с темой, но ответ на который сразу много прояснит.

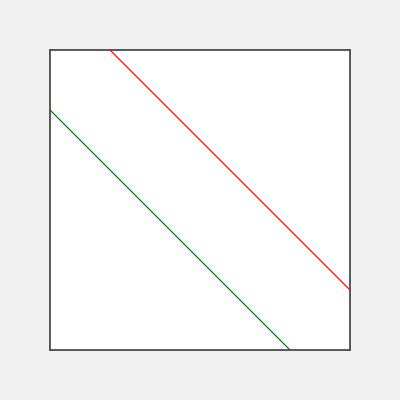Рис. 1. «Две параллельные линии». Канва, браш. Рама.

Перед вами две параллельные линии, с ограниченной областью их просмотра, квадратным окном. Для различия они раскрашены. Вопрос простой: если красная линия это сдвинутая зелёная, то в какую сторону произошел сдвиг?

Варианты:

1. По диагонали вправо-вверх.
2. Вправо.
3. Вверх.
4. Могут быть все три предыдущих ответа.
5. Не только отдельно вверх или вправо, но и все промежуточные направления..
6. Другой ответ, так как некоторые возможности не указаны.

Основы

Представляю вашему вниманию: волна, в самом естественном виде.

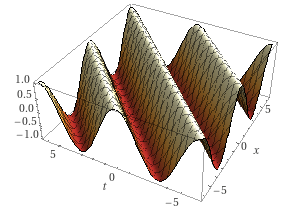
Рис. 2. Волна в движении. (Здесь задумана анимация. Но вместо анимации пространственного среза — функция от пространства и времени)

Что изображено? Пространственный профиль.
Какая особенность? Он движется, и при этом не меняется.
В самом общем смысле волна это соединение пространства и времени через распределённое, но единое содержание.

Разумеется, волна — это больше, чем движение профиля, но для демонстрации этого нужны дополнительные пояснения.

В предваряющей статье о разборе круга рассказывалось о том, как понятие производной дополняет определение круга, это не просто постоянство суммы квадратов координат.

$$

$$

$$

Статья получилось длительной. Было интересно последовательно разобрать одну тему и посмотреть, что получится. Советую читать не торопясь, и только если интересно.

***

Как вам картина (Рис. 1)? Эти две линии напоминают два идущих друг за другом гребня волны. Но правильный ответ на вопрос о направлении сдвига, как ни странно, шестой — «И не только промежуточные». Потому что направление может быть любое, кроме направления вдоль самой линии. Если не допускать отрицательной величины сдвига, то можно, конечно, исключить направления, для которых нужно двигаться в обратную сторону. Но движение по таким направлениям, которые приближены к самой линии больше, чем направление вверх или вправо — тоже вариант.

Например, сдвиг, который складывается из двух шагов вверх и одного шага влево. Сумма коэффициентов при смешивании у шагов вправо и вверх единица, даже если один из коэффициентов отрицательный. Такое, допускающее внутренние варианты, равенство. А с применением комплексный чисел в сумме одно из слагаемых может быть отрицательным, даже если складываются квадраты.

Движение пространственного профиля во времени может быть представлено функцией от двух аргументов, от пространства и времени. Причём, у такой функции значения вдоль диагонали, совпадающей своим направлением с совмещением движения профиля в пространстве и времени, будет сохраняться. Производные такой функции вдоль координаты пространства и вдоль координаты времени будут по абсолютному значению равны, но противоположны по знаку.

Если бы профиль двигался в другом направлении, влево, то производная по пространству осталась бы той же, а производная по времени поменяла бы свой знак, и они стали бы равны.

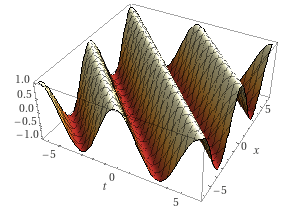По сравнению с предыдущим изображением здесь есть одно простое изменение.

Вторые производные по пространству и по времени будут между собой совпадать. И для функции, сдвиг у которой происходит в противоположную сторону, вторая производная по времени со второй производной по пространству тоже совпадает. В качестве иллюстрации, можно показать, что участок с постоянным ускорением в пространстве выглядит как участок параболы, и если на графике компенсировать постоянную скорость, то относительно точки с этой скоростью график будет симметричен.

Когда говорится о равенстве вторых производных, речь о раздельных направлениях пространства и времени. Направления, совмещающие направления перемещения гребня в пространстве и времени — ведут к неизменности функции, а значит, и нулевым производным вдоль них. Зато, в других совмещениях направлений, в которых пространственное направление противоположно направлению распространения, множитель результата второй производной может доходить до двух.

Если мы возьмём функцию, вторая производная по пространству и вторая производная по времени у которой совпадает, то она позволит существовать не только профилю, движущемуся вправо, или профилю, движущемуся влево, но и функции, которая представляет собой сумму таких профилей. Это и есть дополнительная особенность волны: возможность прохождения через одну точку нескольких профилей в разных направлениях.

Формула волны это равенство второй производной по времени и второй производной по пространству.

$$

Расширение на многомерное пространство выглядит так: для каждого пространственного направления, с различием противоположных направлений, задан свой отдельный профиль, включающий и данные для отрицательных отступов. Такие профили движутся во времени по своим направлениям с одинаковой скоростью.

$$

Где $$ — все пространственные координаты.
$$ — направление в пространстве.
$$ — величина проекции координат $$ на выбранное направление.

Пространственная производная зависит от направления дифференцирования. Общая пространственная производная это вектор, проекция которого говорит о производной в заданном направлении. Вторая производная в прямом и обратном направлении совпадает, общая вторая производная по пространству это число.

Общая вторая производная по пространству это сумма вторых производных по отдельным координатам.

$$

Если отношение значения функции и второй производной для всей области определения постоянно и отрицательно, то функция будет характеризоваться частотой. Коэффициент, отражающий отношение значения и второй производной, будет минус квадрат частоты.

$$

У волн с определённой абсолютной величиной частоты может различаться как знак частоты, так и пространственное направление. В одномерном случае существует четыре вида функций, подходящих под это уравнение, с одним модулем частоты, но с различной зависимостью от времени и от пространства.

$$

$$

$$

$$

Каждый профиль может состоять из набора произвольных комплексных значений, но можно внести дополнительное ограничение. Чтобы профиль, сдвигающийся в положительную сторону, имел в составе только положительные частоты. То есть, сделать так, чтобы знак частоты у каждой составляющей одновременно указывал и сторону распространения, а волн, в которых пространственное направление распространения противоположное, а частота составляющих та же самая, не было.

$$

$$

Другими словами, исключить «сопряжённые волны». И тогда два профиля противоположного направления будут иметь раздельные частотные диапазоны и могут быть совмещены в один профиль, с общим преобразованием по времени.

$$

$$

Частота у частотных составляющих при указания смещения фазы при движении во времени ставится под модуль. Тогда с течением времени части функции, соответствующие положительным и отрицательным частотам, сдвигаются в пространстве в противоположных направлениях.

У движущихся навстречу профилей в одномерном пространстве можно отметить два эффекта:

1. Эффект отражения. Если встречные профили одинаковы вдоль своих собственных направлений, за исключением противоположного знака, то можно найти точку, в которой у профилей совпадают внутренние координаты, сумма в ней приводит к нулю. Эта точка будет приводить к зеркальному эффекту: профиль идущий на эту точку будет как бы отражаться и идти обратно, поменяв знак.

2. Эффект стоячих волн, когда встречные гармонические колебания одной частоты периодически, то гасят друг друга в ноль, то складываются в гребни и впадины, при этом образуя узлы постоянных нулевых значений и пучности колебаний двойной амплитуды, не сдвигаясь ни в одну из сторон. В пространственно-временном распределении это выглядит как сетка из линий нулевых значений вдоль пространства и времени, в квадратных ячейках которой присутствуют гребни, знак которых определяется в шахматном порядке.

При введении ограничения на частоты стоячих волн не будет. Например, такого, чтобы вся плоскость была нулевой, за счёт того, что встречные профили друг друга полностью гасят, а в следующий момент волны появляются — уже не случится. Здесь в отсутствие реальной составляющей о существовании волны будет говорить мнимая составляющая, и наоборот. Общий результат встречных гармонических волн одинаковой амплитуды будет синусоподобная функция, с общим коэффициентом зависимости от времени вида $$.

$$

Из-за введённого ограничения все пространственные частоты, и положительные и отрицательные, относительно времени становятся отрицательными, вращение в комплексной плоскости частотных составляющих при движении во времени выполняется в одну сторону.

Для положительных частот вращение во времени идёт в обратном направлении по отношению к вращению в пространстве. Пояснить это можно на примере болта. У болтов правосторонняя резьба, и чтобы закрутить, нужно крутить болт вправо, по часовой стрелке. Но при закручивании гребень волны приближается к шляпке болта, вместе с прикручиваемой деталью. Поэтому, для того чтобы гребень волны отдалялся, вращение нужно производить в противоположную сторону. Отрицательные частоты и в пространстве закручиваются, наоборот, против часовой, и во времени вращение идёт против часовой, что приводит к отрицательному направлению движения в пространстве.

Если мы видим отсутствие мнимой составляющей у среза функции на определенный момент, это значит, что мнимые составляющие противоположных частот погасили друг друга. В следующий промежуток времени один профиль разойдётся на два одинаковых, движущихся в противоположных направлениях, с появлением противоположных мнимых составляющих. (картинка примера)

Добавление ограничения частот делает производную по времени характеристикой, включённой в пространственное распределение. Вместо содержания отдельно состояния и отдельно данных о его изменении, всё содержится в функции в пространственном распределении, в комплексных значениях. Ограничение возможных состояний приводит к более тесной взаимосвязи составляющих.

Потоки и их столкновение

Перемещение профилей можно воспринимать как поток, как размеренную передачу некоторого ресурса на расстояние. Величина потока больше связана с изменением значения функции, чем с самим значением, так как при постоянном значении можно сказать, что передачи не происходит.

Поток в виде постоянной передачи в случае одномерной функции с действительным значением выглядит как

$$

Производная и по пространству и по времени с точностью до знака даёт величину $$. Но в таком случае значение функции с течением времени выходит за любые рамки.

Если для функции использовать комплексные значения, то постоянная скорость изменения может быть постоянной не сама по себе, а с учётом перпендикулярного движения в качестве изменения фазы, вращения. И тогда чистый поворот в комплексном пространстве будет одновременно и постоянным изменением и изменением ограниченным.

$$

Для двумерного пространства постоянное рассеяние ресурса из точечного источника выражается в распределении величины значения и производной по времени обратно пропорционально расстоянию от источника.

$$

Поток можно интегрировать по контуру вокруг источника с учётом локального направления: интегрировать производные отдельно по составляющей вдоль и отдельно по составляющей поперёк контура.

Интеграл по контуру с заданным расстоянием от источника приводит к постоянному суммарному значению функции, постоянному суммарному значению производной по времени и постоянному суммарному значению пространственной производной относительно контура, что значит, что поток при расхождении сохраняется.

Интересно, что не смотря на то, что распространение занимает время, при условном смещении общего уровня на $$ такое распространение выглядит как мгновенное.

Если величина потока из источника будет зависеть от времени нелинейно, эффекта мгновенности не будет, но интегрально поток на постоянном расстоянии будет равен потоку источника в соответствующий момент.

При действительной функции несколько источников постоянного потока при таком интегрировании по любому контуру, включающему источники, дают сумму величин исходящих потоков.

Если заменить постоянно изменяющиеся действительные потоки на постоянно вращающиеся комплексные, то можно заметить, что при одном источнике для постоянного потока постоянной частоты интеграл по контуру постоянного радиуса даст одно и то же значение, с фазой, которая прямо соответствует фазе источника в момент испускания. То есть, интеграл совпадает с величиной испускания, также, как и в случае действительной функции.

Но если центр у контура интегрирования в виде окружности сместить, то у суммарного потока значение уменьшится, кроме векторного сложения значений произойдёт и комплексное гашение амплитуды, из-за размытия фазы.

Для нескольких разнесённых источников с колебаниями в одинаковой фазе потоки будут накладываться так, что интеграл и значений и производных по окружающему контуру всегда будет меньше, чем сумма потоков самих источников.

Конечно, интересный вопрос, куда исчезает поток, и не стоит ли компенсировать это через различие фаз, а то и изменение амплитуд? Нормировку какую-нибудь произвести… Но есть и более важный вопрос. А ничего, что представленное двумерное рассеяние уже не выполняет волновое уравнение?

Похоже, с двумерным распределением потока волн не так всё просто.

Если взять интеграл по контуру от производной вдоль радиуса, для функции, заданной как распределение волны одной частоты с рассеянием обратно пропорционально расстоянию, получим

$$

При вычислении такой общей для одинакового отступа производной получено дополнительное слагаемое. А это значит, что для соблюдения волнового уравнения рассеяние должно его учитывать, и значит, отличаться от простой зависимости «обратно расстоянию».

Самые простые волны для рассмотрения это плоские. Плоская волна характеризуется тем, что колеблется в пространстве вдоль только одного направления, вдоль всех поперечных направлений она постоянна. Для изучения потоков можно разобрать, как накладывается две плоские волны одной частоты разных направлений.

$$

$$

Первая производная вдоль $$, вместе с самим значением, будет иметь коэффициент, меняющийся как удвоенный косинус вдоль $$.

$$

Частота вдоль $$ снижена до $$. Интеграл у такой производной вдоль $$ будет колебаться около нуля. Похоже, даже частичная встречность потоков требует развития методов расчёта величины суммарного потока.

После расхождения потоки выглядят точно так же, как выглядели бы без наложения, какими сошлись, такими и разошлись. Так что, само распределение потоков при их наложении можно описать как сохранение суммарной величины потока, но с перераспределением отдельных частей вдоль поперечной координаты, в виде коэффициента, создающего области обнуления и области удвоения, обоих знаков. При расхождении это перераспределение возвращает потокам поперечную составляющую.

Рассмотрим ситуацию с двумя точечными источниками волн. Здесь можно предположить, что накладываясь, волны не гасят, а плавно перераспределяют потоки друг друга, изменяют направление распространения, это как мягкая форма такого же перераспределения, которое было в примере с плоскими волнами. На поток будто наложен множитель, оставляющим неизменным суммарное значение по контуру, но производящий перераспределение. И волны в результате даже в некоторой степени концентрируются в общем направлении, подобно лучу лазера, который с расстоянием не рассеивается.

При таком перераспределении суммарная величина потоков должна сохраняться. Наложение колебаний увеличивает удельный поток в месте концентрации, поток переходит туда из мест взаимного гашения. И результат наложения с эффектом концентрации будет превышать результат расчётного наложение волн, рассеянных обратно расстоянию. Но разве амплитуда наложения двух волн может быть больше амплитуд по отдельности? Если рассеяние правильное, то нет.

Правильное — это какое? Суммарно по контуру амплитуда может и не сохраняться.

Самое время разобраться, что именно сохраняется у волны при распространении.

Иллюстрация того, как волны одной частоты от двух источников влияют на максимальную высоту волны в других местах.

Разумеется, при распространении волн сохраняется энергия.

В примере с двумя плоскими волнами энергия двух потоков перераспределяется в энергию двух видов: кинетическую — которая при сложении потоков сложилась не как вектор, а как два числа, и потенциальную, которая в сложенном виде не проявлена, но при расхождении потоков возвращает вклад в поперечное направление.

В гребне волны энергия тоже двух видов: потенциальная, в виде возвышения гребня, и кинетическая, в виде скорости изменения. Скорость входит в энергию как квадрат величины, $$. У плоской гармонической волны поток энергии постоянный, поэтому там, где скорость нулевая, уже квадрат отклонения компенсирует недостающую часть энергии, но с коэффициентом, равным квадрату частоты.

Энергия это действительная величина, её можно считать отдельно для каждой комплексной составляющей, тогда фаза результата не будет удвоена.

$$

Получается, для получения распределения энергии можно либо возвести в квадрат гармоническую функцию, предварительно умножив на частоту, либо возвести в квадрат вторую производную гармонической функции, предварительно поделив на частоту, либо взять со знаком минус произведение функции и её второй производной, что подходит для любых функций.

Общая амплитуда входит в энергию как квадрат величины. Значит, при складывании одинаковых функций суммарная энергия возрастёт в четыре раза. При этом, совсем не пересекающиеся функции дают вклад в энергию линейно, энергией суммы будет сумма энергий. Это значит, что когда при совмещении двух функций требуется сложить энергию, принцип совмещения самих функций уже не является суммой. В таком совмещении для сохранения энергии требуется сбалансировать не только пару функций, а одновременно пару функций и пару их вторых производных. Или пару первых производных по времени, но в квадрате.

Производная по пространству это две составляющих вектора, каждая из которых комплексное число, а в целом это кватернион. А значит, на одну амплитуду приходится три раздельных фазы. Совмещать квадраты двух кватернионов в квадрат третьего меня жизнь не учила, но вполне можно обнаружить, что октонион, как показатель, что куда переходит, на одну амплитуду имеет семь фаз. Не самое удачное время вернуть сопряжённые волны, ведь тогда на горизонте будут седенионы, а там с делением составляющих на амплитуду и фазу уже не всё так просто.

Аппроксимация точечными источниками

Если точечные источники с одной фазой излучения выстроить в ряд, то из всех направлений будет выделяться одно. Для излучения сразу всем рядом в других направлениях нужно сдвигать фазу, в линейной зависимости от позиции в ряду, иначе для этих направлений одинаковая излучаемая фаза будет восприниматься вразнобой, и от этого суммарные волны погасят свою амплитуду.

Подсчитать, как точечный источник излучает гармоническую волну можно двумя способами.

Первый способ.
Сбор волны через сложение профилей для каждого направления полностью согласуется с уравнением волны. От точечного источника излучение волны идёт сразу во все стороны, во всех профилях точка даёт одинаковый вклад. Смещённые в пространстве и времени профили дают вклад обратно в функцию. Так как профиль влияет на соседние направления как проекция, то есть, с растяжением обратно степени сходства направлений – значит, с умножением аргумента гармонической составляющей на степень сонаправленности – то для получения результата суммирования профилей для выбранной частоты нужно проинтегрировать экспоненту с умножением мнимого аргумента на косинус интегрируемого угла.

$$

Осталось избавиться от отрицательных частот, тогда появится ещё и мнимая составляющая.

Существует формула для вычисления этой функции без интеграла.

$$

Второй способ.
Сначала нужно выяснить, как выглядит вторая производная по отдельной координате от произвольной функции радиуса.

$$

Затем сложить вторые производные для обеих координат.

$$

При выборе одной частоты будет верно, что

$$

Но, так как выполняется симметрия масштаба, можно решить с единичной частотой, а затем функцию просто масштабировать.

$$

Решая это дифференциальное уравнение Бесселя, получим функции, которые в реальной части совпадают с результатом первого способа. Если исключить из решения встречное направление потока, от двух констант останется одна

$$

Полученная функция затухает пропорционально квадратному корню расстояния, но в точности с таким распределением не совпадает. Неравномерность отношения есть и в амплитуде и в фазе. В представленном виде общий сдвиг фазы $$, в нуле сдвиг увеличивается ещё на $$. Амплитуда отношения $$ стремится к $$. В нормализованном для приближения к $$ виде функция будет:

$$

Если считать, что волны рассеваются обратно расстоянию, то волны, рассеивающиеся обратно корню от расстояния — на одинаковых расстояниях, начиная с определённого, имеют бо́льшие значения, и их превышающую часть можно считать переизлучением. Правда, тогда вблизи источника обнаруживается и область, где переизлучение отрицательное.

А сами функции Бесселя по модулю в области нуля даже ещё меньше такого рассеяния.

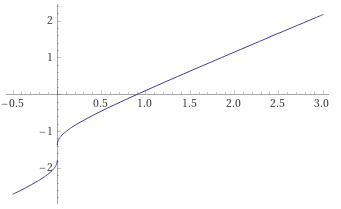
Фаза функции Бесселя.


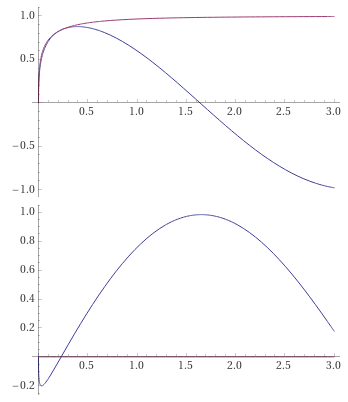
Нормализованная функция Бесселя с компенсацией рассеяния и сдвигом фазы. Видно падение амплитуды в районе нуля. Комплексные составляющие на отдалении больше 0.5 становятся сходны с косинусом и синусом.

Для отрицательных аргументов функции $$ в мнимой составляющей можно задать удвоенное значение $$, чтобы в паре с ней в области отрицательного аргумента изменить знак у реальной части, чтобы волна на отрицательной стороне не была сопряжённой. При компенсации рассеяния функция Бесселя умножается на корень аргумента, для отрицательных значений это будет мнимое число, производящее сдвиг фазы на четверть оборота. Выбором знака корня можно выбрать положительную или отрицательную сторону сдвига.

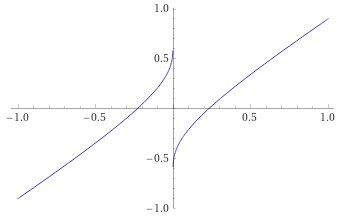Фаза функции Бесселя с компенсацией рассеяния и выбором такого знака у компенсирующего множителя, который выравнивает фазу.

Участок замкнутого контура можно представить состоящим из точечных источников, которые повторяют амплитуду и фазу пришедшей на них гармонической волны от источников изнутри контура. Во внешнем пространстве это будет хорошим приближением волны, за исключением излучения краёв, которое проявляет себя вплоть до добавления оставшихся участков замкнутого контура. В случае замыкания контур сработает как зеркало внутрь, повторитель наружу. Распределение излучения точечных источников должно быть функциями Бесселя, тогда это будет точное представление принципа Гюйгенса.

Концентрические волны

В дифференциальном уравнении $$ координата $$ может быть интерпретирована как величина обратная степени скругления перпендикулярной координаты. Степень скругления, она же степень приближения к центру, будет обозначаться $$.

$$

По любой функции и её производной можно определять локальную частоту вдоль направления, имеющую для каждой точки своё отдельное значение.

$$

Локальная частота может быть комплексной — при изменении амплитуды вдоль направления дифференцирования, в том числе при неравномерном изменении фазы.

Вторые производные можно представить через значение функции и локальную частоту

$$

Координата $$ используется как проекция координаты $$, с условием, чтобы $$.

$$

По этим равенствам видно, что $$ должно быть комплексным. Значит, частота $$ тоже комплексная.

$$

Частотная характеристика энергии делится на две комплексные величины, у которых мнимые части в сумме дают ноль. Эти комплексные величины в роли производных отражаются в негармоническом изменении амплитуды и фазы вдоль перпендикуляра к округлому фронту.

$$

Расхождение фаз у функции и у второй производной по отдельному направлению говорит о процессе концентрации или рассеивании потока вдоль этого направления. Общая вторая производная, суммарная по координатам, при этом может оставаться в той же фазе, отличаясь разве что знаком.

Взаимосвязи

Выполнение волнового уравнения не подразумевает источников потока. Приходится делить одну функцию на две, в отдельном виде выполняющих уравнение везде, кроме областей перевода потока с одной на другую. Относительно источника это внутренний и внешний уровень.

На внутреннем уровне точечного источника волна также центрально-симметрична, только наоборот, концентрируется со всех сторон в одну точку. Можно подробно представить такую волну: так как суммарно энергия по одному значению радиуса постоянна, то постоянен по модулю и окружающий интеграл квадрата значения, умноженного на квадрат частоты, а значит, если локальная частота не меняется, то амплитуда меняется обратно корню от расстояния.

Чтобы разобраться во взаимосвязях можно отметить две особенности в распространении волн.

1. Общая ситуация при простом сложении двух функций это изменение энергии: возможно как дополнительное усиление в два раза, так и полное гашение. Так как при позитивном сложении энергия должна сохраняться, то при суммировании требуется использовать коэффициенты, причём, комплексные. Коэффициенты срабатывают так, что сколько суммарно энергии было в функциях, столько и осталось, но пропорция здесь — это уже отношение двух комплексных чисел, а значит, включает не только количественное отношение, но и степень расхождения фаз, дополнительную вариацию. При выбранной пропорции смешивания вариация разности фаз может отражаться на вариации усиления амплитуды. Можно отметить, что для отдельных двух плоских волн, если у них различаются направления или частоты, коэффициенты не нужны. Если и направление и частота совпали, коэффициенты зависят от различия фаз. Если у волн присутствуют и другие составляющие, то отдельный вклад плоских волн зависит от общих коэффициентов, они же общие.

2. Два представления: представление волны в пространстве как суммы профилей и представление отдельных профилей в координатах угол-сдвиг — были эквивалентными. Но после разбора круговых волн стало ясно, что это не совсем так. При округлении фронта во вторую производную в направлении перпендикулярном радиусу просачивается энергетический вклад из первой производной по радиусу, и этот вклад должен быть скомпенсирован. В представлении угол-сдвиг профили не просто движутся через линию, означающую схождение в точку единым фронтом, а изменяют свою величину — добавляется множитель, сохраняющий энергию при концентрации. Значит, для полного представления волны к данным о профилях должны быть добавлены данные о местах концентрации и о соответствующих множителях.

Добавление источников в волновые процессы добавляет и распределённые множители в профили. Получается, нельзя в профильном представлении просто перекидывать значение на другой уровень по достижению профилем точки, так как это нарушает энергетический баланс.

При концентрации энергия растёт быстрее, чем рассеяние, но она не может перейти в потенциальную энергию, основанную на встрече/расхождении волн. Она переходит в потенциальную энергию, основанную на форме фронта. Условие вклада/возврата у энергии формы это согнутость/разогнутость дуги фронта, производимые изменения при этом — уменьшение амплитуды и сдвиг фазы. Это уже второй вид энергии на основе формы огибающей, первый привносил изменения поперёк потока, а этот вдоль.

Только, сами по себе дуговые фронты не всегда добавляют коэффициент формы. Когда в центр сходятся как прямые так и обратные волны одной частоты коэффициент формы не проявится, получится концентрическая стоячая волна. В этом случае результат не имеет пространственных различий фазы, и представляет собой пространственный профиль с общей фазой, с единым изменением по времени — потенциальная энергия не запасается, потому что тут же забирается встречной волной.

Если рассмотреть по порядку: когда точечный источник выпускает концентрическую волну с обоими знаками одного абсолютного значения частоты, мнимые части гасятся, в результате распределение выглядит как затухающий косинус с единицей в нуле. При компенсации рассеяния функция становится похожей на косинус, сдвинутый по аргументу на $$, и с провалом вокруг нуля. Эта компенсация иллюстративная, её можно в любой момент отменить. Возвращение мнимой части немного компенсирует провал, но волна в результате остаётся сдвинутой по фазе на четверть круга и с повышенной от добавочной компоненты энергией, поэтому применяется коэффициент выравнивания фазы $$, коэффициент выравнивания энергии $$ и коэффициент компенсации различия итоговых амплитуд у пары совпадающих и пары встречных волн одинаковых энергий $$.

Волны обоих знаков частоты из центра во все стороны плоскости

Компенсация рассеяния, восстановление мнимой части

Возвращение фазы

Величина относительного смещения амплитуды. Видно, что без иллюстративной компенсации рассеяния фаза при прохождении точки сдвигается на четверть круга.


Можно рассмотреть волну в контексте изменения размерности. В одномерном случае всё просто — если посреди пространства есть точка перехода, в ней переключаются уровни. На плоскости относительно такой точки надо рассматривать концентрические волны. Они, в дополнение к концентрическому рассеянию, обратному расстоянию, для сохранения баланса энергии усилены на корень от расстояния. Такое усиление ближе определённого расстояния срабатывает как ослабление. Но эффект от балансировки энергии на этом не заканчивается, это ослабление вблизи перехода усиливается дополнительно, при этом меняется не только амплитуда, но и сдвигается фаза.

При переходе через точку фаза проворачивается на четверть круга. А это значит, что если отследить моменты, когда встречные волны различаются на четверть круга, то получим следующее. Разница в четверть имеет направление — сдвинута прямая волна относительно обратной или наоборот. Противоположные варианты вдоль радиуса чередуются. Но при переходе через точку очерёдность переключается. Как будто добавилось или убавилось пространство, причём, размер изменения пространства имеет обратную зависимость от частоты, прямую зависимость от длины волны. Для произвольных волн это выглядит как обмен мнимой и реальной составляющей, с изменением знака для одного из направлений обмена.

Совмещение противоположных частот требует перебалансировки энергии, значит в профильном представлении у встречных концентрических волн присутствуют общие компоненты. Вывод: ясно, что концентрические волны это не плоские, а плоские не концентрические, возможно, стоит поискать и другие типы волн, промежуточные к этим двум видам. «И не только промежуточные».

Огибающие

В уравнении $$ вдоль дополнительной пространственной координаты можно пустить поток выбранной частоты, наложить условие сохранения частоты на производную по времени, а затем посмотреть, какой множитель можно применить в этих условиях к пространственному распределению. Результатом будет не просто коэффициент, обозначающий поворот волны в пространстве, а все допустимые перераспределения. Распределённый коэффициент будет служить для исходной функции огибающей.

$$

$$

$$

Решение:

$$

$$

$$

$$

Получилось уравнение огибающей для волны с одной частотой.

$$

У этого уравнения прослеживаются знакомые черты. Если обозначить $$, тогда можно переписать его так:

$$

Что уже очень похоже на уравнение Шрёдингера:

$$

Для совпадения нужно добавить

$$

Для наглядности можно модифицировать волновое уравнение

$$

$$

$$

Так что, волновое уравнение Шрёдингера — это уравнение огибающей для волны одной частоты, со слагаемым, говорящем о дополнительном измерении, колебания вдоль которого идут с частотой, квадрат которой зависит от разницы квадрата частоты колебания вдоль времени у самой функции и заранее заданной функции $$.

Координаты $$ и $$ — похоже, координаты для разделения внутренней и внешней энергии. Если задать $$, то координата $$ перестанет влиять на волновое уравнение, пространство и время станут равноправны, за исключением присутствия модулируемой волны.

Только, при решении уравнения Шредингера $$ — это исходная функция, а $$ — результат решения. Обратная зависимость невозможна в рамках задачи.

Альтернативный вид уравнения Шрёдингера:

$$

$$

$$

Если исключить встречные по времени волны, то производную второй степени по времени от $$ можно свести к квадрату производной первой степени. Уравнение Шредингера оперирует функцией — огибающей к волне, а значит, индикатором степени перехода энергии в потенциальную.

Частотное пространство

Преобразование Фурье основано на том, что интеграл произведения двух гармонических функций не равен нулю только если их частоты в сумме дают ноль. Два аргумента в интеграле работают вместе, один внутри интеграла проходит пространство, а второй является внешним аргументом, срабатывает как детектор амплитуды для выбранной частоты.

Преобразование переводит функцию из пространственного представления в частотное. При втором применении может перевести обратно в пространственное, только частоты поменяют свой знак, функция развернётся по аргументу, и потребуется нормировочный коэффициент $$ для каждого применения. Суммарной энергией для всей функции можно считать сумму раздельных по комплексным составляющим интегралов квадрата функции. Эта величина при преобразовании Фурье не меняется. Дополнительный общий коэффициент при преобразовании переходит в такой же коэффициент. Произведение двух функций переходит в их свёртку. Свертка переходит в произведение.

Гауссиана — особенная функция.

$$

Особенность в том, что форма частотного распределения этой функции совпадает с формой пространственного распределения.

$$

Каждая из частотных составляющих занимает всю область определения, но все вместе они складываются так, что в центре образуется одиночный всплеск, а чем дальше от центра, тем точнее все частоты компенсируют друг друга. У каждой частоты свой вклад в энергию, но как энергия распределяется в пространстве, определяется только общей, сложенной из всех частот в соответствии с их фазами, формой функции.

С гауссианой при преобразовании Фурье всё просто — когда функцию сужаешь, результат её преобразования расширяется, общая амплитуда, для сохранения энергии, уменьшается. Соответственно, при расширении функции результат преобразования, наоборот, сужается, и его общая амплитуда при этом растёт.

$$

Если гауссиану сдвигаешь в пространстве — у её преобразования сдвигается фаза, пропорционально этому сдвигу в пространстве и пропорционально частоте. Если точно так же сдвинуть фазу у самой гауссианы, то она в частотном представлении тоже сдвинется, только в обратную сторону.

$$

$$

Если захочется одновременно сдвинуть и в пространственном и частотном диапазоне, то надо учесть, что в случае разного порядка выполнения этих сдвигов получатся разные результаты. Если хочется результата независимо от порядка сдвига, тогда надо сначала на половину сдвинуть в одном диапазоне, потом сдвинуть в другом диапазоне, затем завершить первый сдвиг — таким образом закручивание фазы будет в обоих диапазонах вокруг средней точки между пиком и нулём, и порядок будет не важен.

Степень закручивания фазы на пике будет половиной от произведения величин отдельных сдвигов, форма линии одной фазы в фазовом пространстве — гипербола. Преобразование Фурье от сдвинутой гауссианы можно представить плавным поворотом положения пика на четверть круга в фазовом пространстве, со сдвигом общей комплексной фазы, в соответствии пересекаемым при этом гиперболам.

Все функции, раскладываемые на гауссианы, можно подвергать плавному преобразованию Фурье. Для этого придётся различать фазу как множитель и фазу как проявление сдвигов гауссиан. Первая при повороте не меняется, а вторая, пропорционально произведению сдвигов, меняется на противоположную.

Если гауссиану умножать на экспоненту, то это будет эквивалентно её сдвигу и умножению на коэффициент. Если умножать на гармоническую функцию, это тоже будет эквивалентно сдвигу и умножению на коэффициент, который уже сам будет как гауссиана от частоты. Но тогда и сдвиг имеет мнимую компоненту.

$$

$$

Отсюда видно ещё и то, почему гауссиана при преобразовании Фурье переходит в себя: достаточно взять интеграл по $$ в зависимости от $$.

$$

$$

Интеграл гауссианы при константном мнимом сдвиге аргумента не зависит от его величины, так же как при действительном сдвиге. Сдвиг аргумента в мнимую сторону увеличивает общую амплитуду функции обратно гауссиане от сдвига, но неравномерность фазы значения функции вдоль реальной части аргумента уменьшает интеграл обратно на ту же величину, и результат интеграла остаётся тем же самым.

Для того чтобы интеграл гауссианы привести к единице есть два способа: поменять общую амплитуду, поделив на $$, либо умножить аргумент на $$, что будет выглядеть как домножение квадрата аргумента на $$ без деления на $$.

$$

$$

Разумеется, есть и промежуточные варианты, и не только промежуточные. Для $$ при этом можно выбирать любое независимое от $$ значение.

Преобразование Фурье от функции Бесселя имеет интересное аналитическое представление

$$

Это деление на корень из разности единицы и квадрата величины напоминает о теории относительности. Мнимая часть в правой части равенства обрезается — в отличие от того, как мнимая часть аргумента в предыдущей формуле игнорируется.

В продолжение, мнимая часть решения уравнения Бесселя, функция Неймана, преобразуется в ту же функцию, с изменённым знаком под корнем.

$$

Не сказать, что неожиданно. Но интересно, что за волны такие, распределение которых состоит только из функции $$. И что за волны были бы, если бы центральная точка была бы зеркалом, имеющим постоянное значение? А, ну да, если волны концентрические, то это — они и есть.

Тёмная сторона волны

Можно заметить, что встречные волны влияют на первую производную функции так, что в ней остаётся только разница этих волн. А вторая производная не теряет, а складывает соответствующие величины, по Пифагору. Общую вторую производную можно выразить через две первые производные, соответствующих базисным направлениям, а величина гашения будет добавлена отдельно.

$$

$$

$$

$$

$$

Добавочная величина позволяет менять составные частоты, компенсируя все изменения, для сохранения общей локальной частоты. Квадрат величины в основном положительный, поэтому происходит гашение частот. Но может быть и комплексным, чтобы загасить и мнимую составляющую.

$$

В характеристическом равенстве кинетическая энергия выглядит как разница коэффициентов, соответствующих общей и потенциальной энергии.

Чтобы явно задать пространственные составляющие этой величины можно пересечь по две плоских волны для каждого базисного направления, и она даже будет похожа на вектор. Но у вектора все проекции на любой базис согласованы, а здесь распределение по координатам может иметь отдельное значение для каждого направления. Так же как в профильном представлении волны в каждой точке для каждого направления даётся отдельное значение функции, так и здесь для каждого направления разделение величины на вдоль него и поперёк своё.

Впрочем, эта величина выражает прежде всего то, как задана потенциальная энергия, а поэтому представляет собой характеристику огибающей. Огибающая не такое простое понятие — как видно из разбора наложения плоских волн, она может даже менять частоту результата. Если разбирать детально, то нужно учесть, что у огибающей может быть и своя огибающая, значит, придётся разбирать, как несколько последовательных или равноправных огибающих выражаются в одном описании локальных изменений. Сложение двух функций тоже можно рассмотреть как операцию с огибающими.

Тёмная сторона волны представляется мне циклическим потоком внутри каждого отдельного места, энергия вложена, но на приём-передачу не идёт. Но зато она идёт на изменение формы огибающей, а это значит, что может являться вкладом, который забирает совсем не тот, кто положил — а значит, всё равно, в каком-то смысле, передачей.

Третье измерение

При добавлении третьего измерения в профильном представлении в координате направления размерность станет на единицу больше.

Но изменится не только это. Для плоской волны фронт в пространстве уже действительно становится плоскостью, и на ней можно дополнительно выбрать направление колебания, появится поляризация. Это проводит к делению одной волны на две составляющие, по одной на каждое базисное направление, перпендикулярное к направлению распространения.

Причём, у каждой части не только своя амплитуда, но и фаза — парная волна может повторять в мнимой составляющей реальную, а в реальной мнимую, с изменением знака для одного из направлений. Для таких волн оценку энергии можно делать исходя только из реальных составляющих. Конечно, парная фаза может и просто совпадать с исходной. А может быть так, что в парной составляющей будет нулевая амплитуда, что делает добавление поляризации похожим на возвращение сопряжённых волн — те похожим образом гасят поперечные колебания в комплексном пространстве. Но деление на две составляющих даёт явное развитие по сравнению с волнами на плоскости.

Из-за такой поляризации значение у пространственного распределения волны становится вектором. Дать общее пространственное направление у вклада два профиля могут только если направления их распространения перпендикулярны этому общему направлению. Иначе вклад профиля вместе с отличием от перпендикуляра уменьшается, а вклад в другие направления, в степени сходства с общим перпендикуляром, увеличивается. Получается, чем более сходны направления у значения и распространения, тем меньше вклад.

Очень подозрительно, когда значение функции похоже на всё что угодно, только не на направление распространения.

Поделить волну на две части можно и по-другому.

Волновое уравнение — это равенство вторых производных по пространству и по времени, а в трёхмерном пространстве уже для первых производных по пространству и времени можно обозначить выражение равенства, но — только для разделённых между собой полей.

У таких полей для каждого их всех трёх базисных пространственных направлений задано своё значение. Производная по времени одного поля одной составляющей будет пространственной производной другого поля во втором направлении от составляющей третьего направления. А так как таких соответствий два, то одно значение делится «на двоих», пропорция подбирается на месте, и для одного из направлений изменён знак. От второго поля к первому такая же зависимость, только, тоже, изменён знак. Не сложно правильно расставить знаки, самосогласованных вариантов — как вариантов вращения, всего два.

$$

$$

$$

Два поля остаются одной волной, их взаимное переизлучение — это условность в рамках последовательного восприятия времени. Обе части волны летят ровно так, как их выпустил источник — так же как волна в профильном представлении идёт по своему направлению, не меняясь, особенно когда нет препятствий.

Будем разбираться как связаны эти два представления. Сравним количество локальных характеристик. В профильном представлении итоговое пространственное значение это три числа, поляризация умножает на два, итого шесть. В полевом представлении по три действительных составляющих на два поля, итого составляющих тоже шесть. Совпадает, можно разбираться дальше.

Для этого надо разобраться в векторном произведении двух векторов. В нём нет ничего сложного, как и в произведении двух комплексных чисел, амплитуду можно подсчитать отдельно, фазу — или уже направление — отдельно. Амплитуда, разумеется, является произведением, только добавится множитель, равный косинусу отличия угла между векторами от прямого. А вот направление у результата имеет две особенности. Первая особенность — что результат перпендикулярен двум исходным направлениям. А вторая особенность — что, так как таких перпендикулярных направлений два, выбор зависит от последовательности аргументов умножения. У базисных векторов в пространстве есть порядок, один из двух вариантов, и векторное умножение можно считать операцией, сохраняющей этот порядок.

Произведение двух векторов можно представить определителем матрицы. Матрица — вектор, составляющие которого — тоже вектора, одинаковой размерности. Определитель матрицы — это величина объёма параллелепипеда, составленного из составляющих матрицу векторов. Но если из трёх трёхмерных векторов один вектор имеет в составе не величины, а три вектора от базиса, то определитель станет тоже вектором, это и будет векторное произведение. В такой математике, в которой самая сложная операция — вычисления объема параллелепипеда, нет ничего сложного. Но если первый аргумент умножения будет содержать вместо вектора оператор производной по базису, определитель матрицы превращается в ротор.

$$

Если бы мы на плоскости вместо определения площади параллелограмма $$ один из векторов превратили бы в производную: $$, то у нас получился бы индикатор степени вращения значения функции вдоль плоскости. Стало бы ясно, как вектор сдвигается вверх при смене координат вправо, и как вектор сдвигается влево при смене координат вверх, и, из-за линейности на малых расстояниях, в любых линейных комбинациях этих направлений тоже. Получилась одна скорость поворота на все направления смены координат.

В объёме всё точно так же, только результат не число, а вектор. Значит, ротор — это тоже индикатор вращения. Вот кто бы знал. Казалось бы, волны и вращение — какая может быть связь? Придётся разбираться и в этом.

Вращение

Рассмотрим поворот на плоскости. У плоских волн выполнить поворот просто — надо притормозить волну в прямом направлении, умножив на коэффициент $$ и разогнать в перпендикулярном направлении, умножив на $$. Это перемещает вклад выделенной частоты профиля в профиль другого направления той же частоты, больше ничего.

Для концентрических волн поворот тоже возможен. Чтобы не нарушать концентрическую форму, его нужно выполнить в профильном представлении как добавление смещения у профиля, по направлению движения, с линейной зависимостью от направления. Если сдвиг фазы будет одиночно кратен обороту направления, тогда профили противоположных направлений будут сходиться в центре в противофазе, а это говорит о постоянном значении, и значит, зеркале в точке схода. Если там будет зеркало, возможности сконцентрировать весь фронт в одной точке и выкинуть на другой уровень уже не будет.

Определим значение профиля и проинтегрируем, чтобы получить значение функции вдоль одного направления.

$$

$$

Вот это да. Опять функция Бесселя. Теперь с индексом $$.

$$

$$

$$

Уравнение Бесселя, три формулировки и решение:

$$

$$

$$

$$

$$

$$

$$

График функции $$.

Распределение амплитуды.

Мнимая составляющая

Распределение является решением уравнения Бесселя, как соответствия общей второй производной, взятой как сумма вторых производных по радиальному и тангенсальному направлениям — при единичной частоте самому значению функции, взятому с минусом.

$$

Во вторую производную по тангенсальному направлению входит проникновение первой производной по радиальному направлению и отражение энергии, ушедшей на закрученность.

Иллюстрация границы фаз. Распределение со временем вращается.

При разделении координат на радиус и направление

$$

Сама функция будет равна:

$$

Это выглядит как прохождение волны перпендикулярно радиусу, вдоль окружности. Циркуляция волны по кругу звучит странно, как может кружиться волна без источника?

При рассмотрении аналогии со сложением двух плоских волн можно сделать вывод: кручёная концентрическая волна в процессе пересчёта волны из до-потенциальной в после-потенциальную, с выделением огибающей, сталкивается сама с собой и идёт в новом направлении.

У закрученной концентрической волны, так же как было с обычной концентрической волной, можно восстановить мнимую составляющую, функцию $$, являющуюся линейно-независимым решением того же уравнения. Распределение на плоскости, с зависимостью фазы от направления, состоит из таких же колец, только сдвинутых вдоль радиуса. Результат соединения зависит от направления вращения и заданной фазы. Однообразно соединять можно двумя способами, в зависимости от знака мнимой части.

$$

Амплитуда функции с однообразно восстановленной мнимой частью центрально-симметрична. 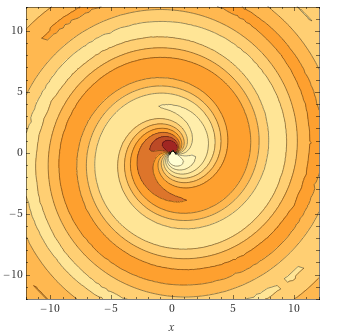Но отдельно реальная и мнимая составляющие выглядят как спираль. Если у $$ поменять знак, направленность спирали изменится на противоположную.

Отдельно $$ и $$ не производят переброса энергии через центр, так как каждая является своим отражением в центре, вдоль радиуса имеет нули и является стоячей волной, кружащейся вокруг центра. Но при соединении вместе, с образованием спирали, нули пропадают, и в центре, так же как было при совмещении частей у не кручёной волны, будет переброс, с зависимостью направления переброса от знака мнимой части. Если, конечно, не считать, что кроме вращения ничего не происходит — а наблюдая за крутящейся спиралью можно подумать и так.

Интересно, как такое распределение, движение которого во времени выглядит как вращение результата в пространстве, выглядит в профильном представлении? Может быть, так же как у повёрнутой концентрической волны — со сдвигом, пропорциональным направлению — только, мнимая часть по каким-то причинам не гасится? Это говорит о том, что при учёте стоков и источников профильное представление будет расширено — например, разделением в пространстве областей для вкладов встречных профилей.

Производные

Для функции от нескольких координат производная это функция, которая показывает, как меняется исходная функция вдоль каждого из направлений этих координат. Получается, сколько координат, столько значений — то есть, это вектор. Чтобы получить эту векторную функцию, нужна функция от функции, то есть, оператор. Обозначается как $$, градиент. Вектора, чтобы отличать их от скаляров, будут обозначаться заглавными буквами.

Если мы на плоскости возьмём две функции — по одной на координату, то производная будет иметь четыре значения — с делением на два по тому, от какой функции берётся производная, и с делением на два, по какой координате. Среди этих значений — два значения будут взяты по своим координатам, а два значения по противоположным. Для векторных функций на плоскости можно выделить две производных, состоящих из сумм этих значений.

$$

$$

Функцию с комплексным аргументом и комплексным значением можно считать за две действительных функции на плоскости. Изменение комплексного аргумента для таких функций приводит к изменению комплексного значения — но относительно существующего значения функции любое изменение можно поделить на изменение амплитуды и изменение фазы. Этим величинам и соответствует дивергенция и ротор. Зная эти производные можно определить изменение комплексного значения по выбранному изменению комплексного аргумента.

Обе характеристики весьма информативны. Если бы векторная функция на плоскости обозначала направление движения, то не нулевой ротор говорил бы о тенденции ходить кругами. Не нулевая дивергенция говорила бы о том, что количество идущих не постоянно. Можно ясно представить, как элементы массы движутся, и движение спровоцировано двумя способами: либо в каком-то месте элементы добавляются и требуют распределения, вплоть до места, где их обратно забирают, либо происходит хождение кругами. Либо и то и другое вместе.

Ротор показывает степень изменения направления перемещения, и такой поворот это вовсе не следствие включённости элемента в поток распределения, это всегда противодействие такому потоку. А дивергенция показывает как распределён по пространству источник, из которого приходит то, что движется по векторному направлению значения функции.

У функции, полученной градиентом, движения элементов согласованы и нет тенденций кружить — ротор любого градиента будет нулевой. Ротор убирает все признаки источника, почему-то даже у результата, дивергенция от ротора ноль. Ротор для пространства удобней обозначать $$, а дивергенцию $$. Можно подсчитать ротор ротора — степень эффекта, когда сама тенденция кружить имеет тенденцию кружить на другом уровне.

$$

$$

$$

$$

$$ — Лапласиан, показывает степень пространственной изогнутости, в виде суммы вторых производных по базисным координатам. Другими словами, общая вторая производная. Если лапласиан равен градиенту дивергенции, то ротор ротора нулевой. Так же как на плоскости: если умноженная на значение функции сумма вторых производных равна сумме квадратов первых производных, то «тёмной» части в волне нет.

$$ — расчёт источника векторного произведения приводит к разнице двух скалярных произведений вектора и ротора другого вектора в различном порядке.

В пространстве для волны, представленной функциями $$ и $$ выполняется

$$

Брать производную по времени и вычислять ротор для векторной функции можно в любом порядке, результат будет одинаковый. Поэтому можно определить функцию $$, такую, что будет выполняться соотношение

$$

$$

$$

Дальше можно поделить функции $$ и $$ каждую на две части.

$$

От $$ отделится градиент одного скалярного поля, а в $$ отделится градиент другого скалярного поля, связаны через производную по времени. Так как ротор градиента это ноль, на $$ это не окажет влияния. Но скалярное поле в $$ отделяется так, что будет выполнять условие, что его производная по времени обратна дивергенции оставшегося $$.

$$

И тогда будет выполняться второе соотношение

$$

$$

$$

Где $$ — функция для учёта источника волны, степень отклонения от волнового уравнения.

Если проследить за тем, что соответствует источнику поля, которое является векторным произведением полей

$$

$$

$$

То получим уравнение сохранения энергии, которое говорит, что отдельные плоские волны идут в направлении, перпендикулярном к обоим полям и амплитуды полей при этом одинаковые.

Сама функция $$ это волновое излучение, источник которого распределён в виде $$:

$$

Оставшийся вывод:

$$

В итоге вся схема выглядит так:

$$

Между $$ и $$ есть связь, которая имеет простое представление:

$$

И расширенное:

$$

И они согласованы между собой. Но то, что связь между $$ и $$ не прямая можно показать и более явно. Опосредованность заключается в возможности существования промежуточного поля $$, которое добавляет вклад в изменения со временем $$, через вихревую форму распределения в пространстве.

$$

Опосредованных связей во всей системе уравнений несколько, их можно продемонстрировать так: то, что находится в квадратных скобках не влияет на равенство.

$$

Опосредованную связь можно показать на примере первого же уравнения всей системы, $$, в нём распределением $$ по всему пространству мгновенно задаётся величина заряда. Но можно заметить, что связь является опосредованной через дивергенцию. Обратная связь позволяет такое распределение поля, в котором конкретные значения смещены, а величина смещения распределена так, что не даёт вклада при вычислении дивергенции. А значит, обратное влияние заряда на поле не обязательно мгновенное.

Изменение распределения заряда может мгновенно изменять одну часть распределения, но при этом будет менять и другую часть, которая полностью отменяет влияние до тех пор, пока до тех мест не дойдёт сигнал об изменениях, а когда это будет — совсем другое вопрос. Может вообще не дойти, если отменят. То есть, даже просто поле $$ из-за опосредованной связи с зарядом можно разделить на безвихревое поле мгновенного распространения и компенсирующее всю мгновенность вихревое поле.

Поляризация

Чтобы выяснить, как связаны три различных представления волны, нужно рассмотреть связи их компонентов. Профильное представление содержит комплексные числа, количество которых для отражения поляризации расширено до двух. Представление через поля имеет по два поля, по три действительных компоненты для каждой пространственной точки. Для промежуточного представления, в котором так же как у профильного для выделенного направления и сдвига задаётся значение, которое представлено векторным произведением полей, состав может быть дополнен характеристиками, дающими возможность их восстановления. В рамках плоскости, перпендикулярной к произведению, в качестве поляризации даётся направление $$, без указания модуля. И дополнительно — скалярные характеристики $$ и $$.

Количество компонент: полевое представление: $$, промежуточное представление: $$, волновое представление: $$. Количество компонент промежуточного представления легко довести до шести, включив все дополнительные характеристики. Для того, чтобы в профильном представлении компонент стало шесть, поляризацию нужно расширить, допустить третье измерение — поляризацию вдоль распространения.

Здесь и заключается тонкая грань между представлениями. В профильном представлении третье направление поляризации считается характеристикой источника, а не поля. Если в поле сохраняется поляризация вдоль направления распространения, это значит, что действие источника ещё не прекратилось, профили не разошлись. А с другой стороны, что, жалко что ли добавить третью компоненту? Да не жалко. Пусть летит волна, одна из компонент которой вдоль направления движения — значит, в каком то смысле, вдоль времени.

В целом, получилось интересное поле — характеризующееся шестикомпонентным числом, совмещающим три комплексных числа, или два вектора — способов разделения на компоненты несколько. Но в промежуточном представлении вектор совпадает с направлением движения, а значит, количество скалярных компонент не три, а одна. Похоже, для чистых волн без связи с источником, их действительно только четыре. Так что, вопрос количества компонент поляризации — это вопрос сохранения связи волны и её источника. На связь уходит как минимум две компоненты из шести.

Источники и стоки

Рассматривая сток/источник посреди спирали можно сделать вывод, что источники могут быть разные: один вид испускает во все стороны волны, соответствующие значению в центре, другой вид имеет нулевое значение в центре, а волны противоположных направлений имеют противоположные фазы. Да ещё и вращаться можно. Если говорить о соответствующем стоке, он тоже выполняет свою функцию: перевод энергии на другой уровень точно так же не даёт волнам встречных профилей зайти на общее пространство.

Два источника, отправляющие волны на встречу друг другу, могут рассчитывать на два варианта событий: на пространственное наложение встречных волн, с компенсацией потока энергии, или на нахождение между ними стока, который проведёт волне смену пространства, забрав энергию.

Волны задаются распределением источников, а сами источники имеют правила распределения, включая правила движения и реакции на приходящие волны. В целом, статья про волны закончена, осталось небольшое исследование возможных распределений источников и совмещения волн и источников вместе.

Распределение заряда и распространение волны может представлено в различных пространствах, для соотнесения пересчитываемых между собой через свёртку. При размытии функции результат получается свёрткой с профилем размытия. Преобразование Фурье заменяет свертку двух функций на произведение значений для одинаковых частот. Но у размытия есть и обратная операция: наведение чёткости — свёртка с обратным для исходного профилем. Обращение профиля достаточно простое действие, если нет частот с нулевой амплитудой. Когда есть два пространственных распределения: заряда и волны, и одно из них размыто, то можно произвести наведение чёткости. То что было размытым — станет чётким, а вот тому, что было обычным, придётся стать сверх-чётким. Что, вполне ожидаемо, позволяет появиться повсеместному ненулевому заполнению, исчезающему при размытии.

Преобразование Фурье от гауссианы

$$

даёт интересные следствия. Одно в том, что если обратить знак у $$, знак у обоих функций может остаться одинаковым. А второе, что при $$ можно подобрать такой общий коэффициент для обоих сторон, при котором преобразование Фурье от действительной функции даст функцию с исключительно мнимыми значениями. Здесь нужно обратить внимание, что при прохождении $$ через ноль функция как бы выворачивается наизнанку. А у гауссианы, у которой в $$ абсолютная величина мнимой части больше абсолютной величины реальной — тоже происходит выворачивание, по уровню, и энергия для такой функции при интегрировании перестаёт сходится.

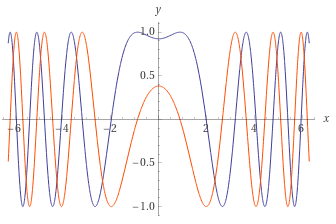
График функции $$, это гауссиана при $$



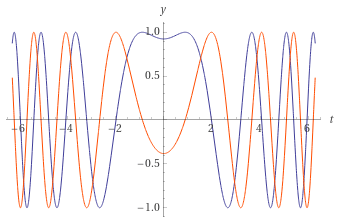
И её преобразование Фурье, $$. Отличатся знаком мнимой части.


При противоположных значениях $$ правила соответствия знака противоположны, и если абсолютное значение мнимой части больше абсолютного значения реальной, то для положительной величины мнимой части и для отрицательной правила тоже будут противоположны. Значит, есть четыре правила, при прохождении по кругу они последовательно меняются. Без меняющихся правил схема знаков будет выглядеть как край ленты Мёбиуса: при переключении на противоположную сторону — два равнозначных варианта.

$$

Здесь $$ — символ неопределённости знака, участвующий как множитель с зависимостью от $$. В самом простом виде он повторяет минус, если $$ отрицательное число.

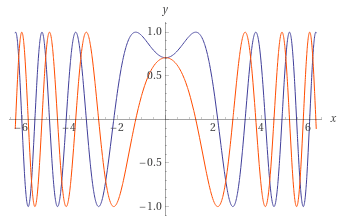
График функции $$, это гауссиана по второй формуле при том же $$



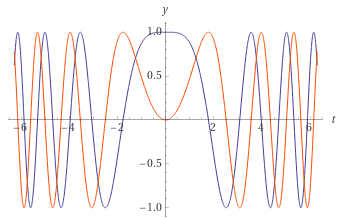
И её преобразования Фурье, $$.

Распределение источника может быть точечным, может быть гауссианой, а может быть расширенной гауссианой, с единичной амплитудой по всему простраству, из-за распределения фазы дающее единичный интеграл.

Реальная часть интеграла от расширенной гауссианы. Похожа на ступеньку, соответствующую точечному источнику.

Диаграмма интеграла расширенной гауссианы в комплексной плоскости. Пример перемещения из одного пункта в другой при постоянной скорости, без резких изменений направления и без ограничений по времени.

Квадрат коэффициента можно представить в виде суммы реальной и мнимой составляющей.

$$

$$

Теперь видно, чему знаковый множитель пытается соответствовать. Соответствие преодолевает даже то, что корень для комплексных чисел не разделяет варианты значений на положительные и отрицательные.

Что у коэффициента $$ больше по абсолютному значению, мнимая часть или реальная, определяется только знаком величины $$.

$$

$$

$$

Изменением одного только $$ не получится перейти через границу по энергии, изменение $$ пойдёт по гиперболе, не пересекающей диагональ.

Преобразование Фурье сохраняет энергию функции — каждая разделённая по области аргумента часть функции содержит одинаковую энергию до и после преобразования. При суммировании частей функции результат зависит от их пересечения. В исходной функции части поделены по аргументу. Результат преобразования из-за различия частот также не содержит влияния частей не энергию других. Но и при плавном преобразовании Фурье каждая часть перераспределяется так, что вместе с преобразованием других частей наложение происходит без изменения энергии функции.

Рассмотрим, какое влияние на энергию оказывает изменение коэффициента $$.

Норма интеграла позволит выводить энергию без отношения к расходящемуся интегралу как к исключительному случаю.

$$

Развернём коэффициент, вынесем неопределённость знака в знаковый множитель

$$

Различие между квадратом функции и покомпонентным квадратом проявляется в различных результатах:

$$

$$

Косинус в квадрате и синус в квадрате выразить через экспоненты просто:

$$

Части внутри скобок можно каждую отдельно скомпоновать с экспонентой, стоящей перед скобкой под интегралом. А вот то, что для каждой из трёх частей знак интеграла будет своим, надо учитывать. И хотя при положительном $$ они будут одинаковы, в других случаях у них может быть четыре комбинации. Это два в степени количества бинарных характеристик, но с учётом, что общий знак влияет на линейность.

$$

Теперь надо вывести выражение для энергии заданной гауссианы.

$$

$$

Рассмотрим эту сумму по частям, первое и второе слагаемое отдельно.

$$

Эта функция по горизонтали не симметрична. Она распределена в виде кардиоиды.

Фигура кардиоиды — это проявление механизма, когда один единичный круг вращается вокруг второго единичного круга, зацепившись как шестерёнка. Видимо, это ещё и волновой механизм. Для построения кардиоиды нужно сложить два единичных вектора, только один из них нужно поделить пополам: одна половина будет постоянного направления, а угол направления другой будет удвоенный относительно угла второго вектора.

$$

$$

$$

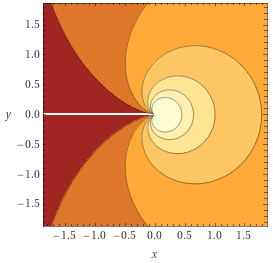
Несколько уравнений, задающих кардиоиду выбранного размера:

$$

$$

$$

$$

Размер можно наоборот, определить по координатам

$$

По размеру можно определить значение функции

$$

Как видно, не только произведение $$, но и сумма корней имеет короткое обозначение.

$$

Всё это может казаться сложным, но если принять $$, $$, то при построении графика в зависимости от $$ из кардиоиды функция превращается в две окружности:

$$

$$

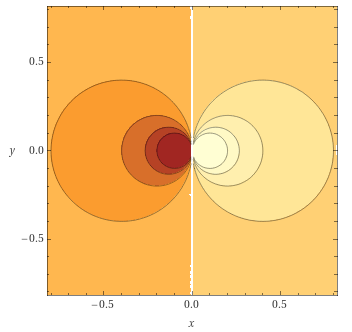
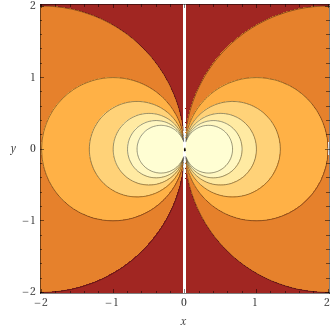
Знак функции при отрицательной реальной части $$ определяется тем, учитывали ли мы дополнительную бинарную координату — знак величины $$ — при задании изначальной функции, или задали функцию только для одного её значения, а для другого знак можно обратить.

Если знаки у правой и левой части первого слагаемого не совпадают, то направление кардиоиды вдоль горизонтали меняется, значение функции становится мнимым, и кроме того, при переходе через $$ будет меняться знак. График по координатам $$ будет двумя окружностями, расположенных в вертикальном порядке, и у них будет смена знака по вертикали. Смена знака по горизонтали тоже будет, но её можно убрать так же, как можно было добавить в предыдущем случае.

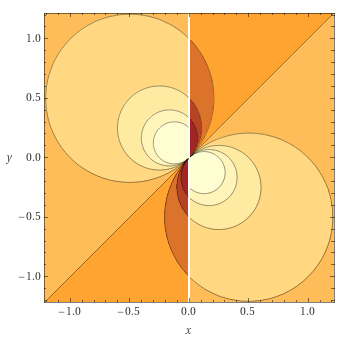Если вдруг $$ перестанут быть бинарными значениями, и станет верным $$, тогда и реальная и мнимая часть будут иметь одинаковое распределение — круги, повёрнутые на восьмую часть оборота. То есть, фазовое вращение $$ распределяется на пространственное и фазовое вращение результата, каждое с половинной скоростью. Пространственное вращение — так ещё и в обратном направлении, в отличие от $$.


Второе слагаемое энергии зависит от одного действительного числа и график в координатах $$ представляет собой гиперболу с мнимым значением для положительного аргумента, реальным для отрицательного, и зависимостью знака результата от $$.

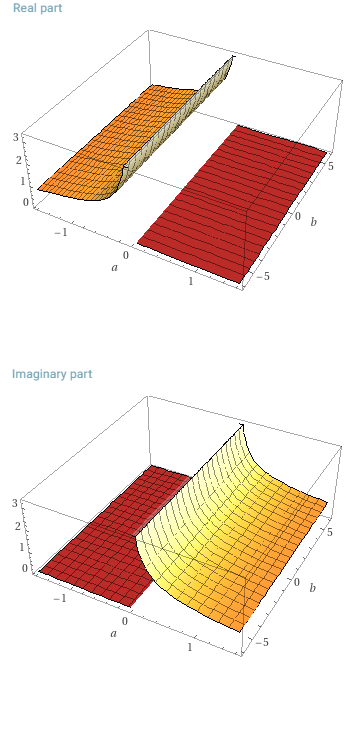
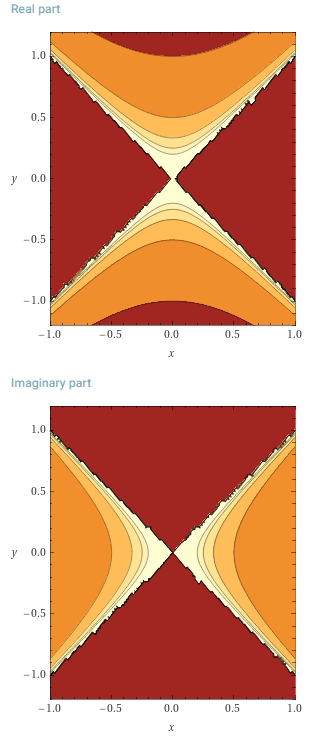
Деление на $$ превращает сумму исходных составляющих в реальную составляющую, а разницу в мнимую. При таких поворотах сумма обеих составляющих результата соответствует мнимой части исходного числа.

Энергию можно расписать немного шире.

$$

И тогда при использовании обращённых координат

$$

Дроби будут оставаться на своих местах:

$$

Кроме упрощённой замены переменных $$ и добавления множителя $$, знаковые множители $$ и $$ как будто поменялись местами. Пока они одинаковые это ничего не значит.

Преобразование Фурье гауссианы в аспекте преобразования энергии можно записать как

$$

$$

$$

$$

Если к функции добавляется множитель, то модуль энергии меняется соразмерно квадрату модуля этого множителя. По приведённому выражению для энергии видно, что при единичных гамма-коэффициентах модуль комплексной энергии сохраняется. Так как энергия функции это сумма раздельных по комплексным составляющим интегралов квадрата функции, то важен не модуль результата, а сумма составляющих. Множитель, меняющий фазу исходной функции, изменяет только разницу составляющих результата, и не влияет на конечное число.

***

Преобразование Фурье служит методом пересчёта движущегося профиля в статичные колебания, образующих движение только совместным действием. Одно такое колебание выделенной частоты не различается в пространстве по амплитуде и не различается по пространству и по времени иначе, чем по стабильно меняющейся фазе. С одной стороны, энергия должна сохраняться, так как это свойство смены представления одного и того же процесса. Можно даже попробовать источники, со всем их процессом изменений включить в систему рассмотрения с другого ракурса. Но с другой стороны, дополнительные преобразования проявляются внутри преобразования Фурье как дополнительные характеристики, и здесь кое что не ясно — они задают сохранение энергии, или подчиняются ему?

Можно запутаться, но я, вспомнив принцип болтика, понял: к чему прицепился — то и не двигается. То есть, вопрос взаимосвязи функции и энергии зависит от того, кто спрашивает: физик или математик. И физик, который исходит из того, что энергия сохраняется, бывает не прав — так как этим отсекает передачу её в ещё неизвестных направлениях. Не смотря на то, что действительно, что сохраняется — то и энергия. Математик может разобраться, каковы условия сохранения энергии. Но и в математике есть принципиальные недостатки: можно незаметно для себя всё слишком упростить. Это видно на примере задачки про линии. Только физика может напомнить, что практика важнее математики. Физика открыта новому, поэтому часто движет математику. Математика же принципиально не может разделить автоматическое упрощение и непрактичность.

Энергия

Отличие энергии, использованной для определения энергии волны, от энергии, полученной через покомпонентное интегрирование квадратов функции в том, что для волны результат составляет энергию не самой функции, а её производной. Она могла быть определена через произведение значения функции и второй производной именно потому, что в этом случае множитель локальной частоты распределяется, и остаётся только один раз на функцию. Он отражает относительную скорость изменения, вместе со значением функции становится просто скоростью, и общее значение возводится в квадрат. При вычислении энергии через интегрирование квадрата функции постоянная составляющая даёт весомый вклад в энергию. Но если энергию брать от производной, то перед возведением в квадрат этот вклад умножается на частоту — и у нулевой частоты вклада не будет.

У нас есть пара типов энергии. Уже вполне ясно что с этим можно сделать, искать другие.

Значение функции и энергию с остатком фазы в заданной точке можно представить как

$$

Выражение для соответствующей энергии можно немного развернуть, чтобы реальная часть отражала сумму составляющих.

$$

$$

$$

$$

$$

Предоставленное для вычисления энергии одиночное значение можно распределить в интегрируемую функцию от дополнительных аргументов — на величины, квадраты которых могут давать в реальной части отрицательные числа, но при этом общая сумма сориентированных квадратов своей реальной частью будет сходится к фиксированному числу.

Зададим функцию, вклад в различие составляющих у энергии которой будет зависеть от аргумента. Два варианта поворота.

$$

Для этих выражений можно по тем же принципам рассчитать энергию.

Получилось два интеграла

$$

Реальная часть сохранилась. Мнимая часть зависит от поворота исходного интеграла.

Просчитаем вид интеграла в общем виде для всех направлений

$$

$$

Обобщим на комплексную функцию

$$

$$

$$

Этот интеграл не зависит от поворота. Можно даже скорректировать значение функции, поделив на расстояние до точки, $$, и тогда энергия будет просто суммой покомпонентных интегралов квадратов функции.

Мнимая часть зависит от удвоенного угла.

$$

$$

$$

Если множитель $$ перенести внутрь функции $$, то во втором множителе останутся такие слагаемые:

$$

$$

Интеграл зависимого множителя при синусе симметричен, сходится к нулю.

$$

Но этот результат соответствует только константной функции. Как влияет он на произвольную функцию можно рассмотреть через его преобразование Фурье.

$$ и $$ сами будут комплексными? Или распределёнными функциями?

***

Сначала в продолжении я хотел объяснить устройство спина, свойства источника волн в условиях, когда волна задаётся не через изменение величины заряда источника, а через его движение, при этом ещё и сам заряд реагирует на волну. Почему вдруг гамма-коэффициенты обретают новые закономерности, и почему появляющиеся вновь коэффициенты уже сами как функции, а то и как добавочная метрика? Как это всё выглядит со стороны? Но при обстоятельном подходе придётся объяснять и то, как пользоваться болтиком. Только, я считаю, что каждый в этом должен разобраться сам. Это же самое простое что вообще может быть! Так что, но этом пока всё.

Как устроены волны? Как и всё — непреодолимо загадочно. Но из них, как и из всего, можно сделать зеркало. Чтобы разгадать главную загадку. А зачем ещё они нужны?

---

Сегодня международный день полёта человека в космос, и день космонавтики.
Шестьдесят лет назад человек вышел в космос! Поздравляю вас с этим праздником.