Как Осборн Рейнольдс пришёл к своему числу. Часть 5

Пуазейль проводил эксперименты в стеклянных капиллярных трубках диаметром от 0.02 до 0.1 мм. Применимость его формулы для расхода к гладким металлическим трубкам размером в 100 раз больше представляет большой интерес.

Формула Пуазейля.

Q = 1836.724 (1 + 0.0336793 T + 0.000220992 T²) H D⁴ / L,

T = температура, °.

H = давление, мм. рт. ст.

D = диаметр, мм

L = длина, мм

Q = расход, мм³.

Пусть i = 13.64 H/L.

P = (1 + 0.0336793 T + 0.000220992 T²)^-1.

v = 4Q / (πD²).

Переведя единицы в метры и кубометры, формулу можно записать ка.

47700000×(D³/P²)×i = 278×(D/P)×v, при этом коэффициенты соответствуют A_c и B_c.

Сразу видно, что эта формула согласуется с экспериментальными результатами для трубок 4 и 5. Измеренные и расчётные значения расхода отличаются менее чем на 2%, что более чем объясняется разницей в температуре в полградуса.

35. За критической точкой.

По таблицам видно, что за критической точкой отношение i и v сильно отличается от константы; но из таблиц нельзя определить, как именно они связаны, и насколько эта связь универсальна для двух трубок.

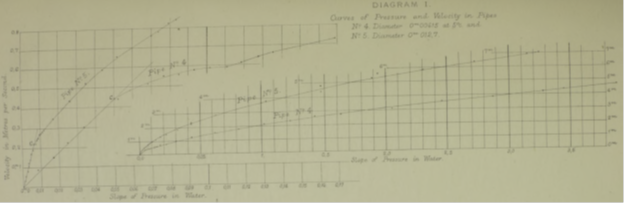
На графиках зависимости v от i (диаграмма 1) после прямолинейного участка кривые принимают вид парабол; однако неясно, являются ли они в точности параболами, если просто их сравнивать друг с другом, а также насколько они подобны друг другу. Чтобы на графике были видны маленькие разницы в давлении, он должен быть длиной как минимум 3 метра.

36. Логарифмический метод.

Пока что мы сравнивали результаты в естественных единицах, но если рассмотреть логарифмы i и v, получается более ясное и полное сравнение.

Этот метод обработки результатов экспериментов был предложен в моей работе по тепловой транспирации (Phil. Trans., часть II, 1879, стр. 753).

Итак, возьмём в качестве абсциссы и ординаты не i и v, а их логарифмы. Такие кривые будем называть логарифмическим представлением обычных кривых.

Преимущество логарифмического представления в том, что форма кривой перестаёт зависеть от каких-либо постоянных параметров, которые на все точки логарифмической кривой влияют одинаково. Если в естественном виде кривые похожи друг на друга, то в логарифмическом виде они становятся идентичны. В случае нашей задачи эта методика работает очень хорошо, как видно на диаграмме II, где приведены в логарифмическом виде данные для трубок 4 и 5.

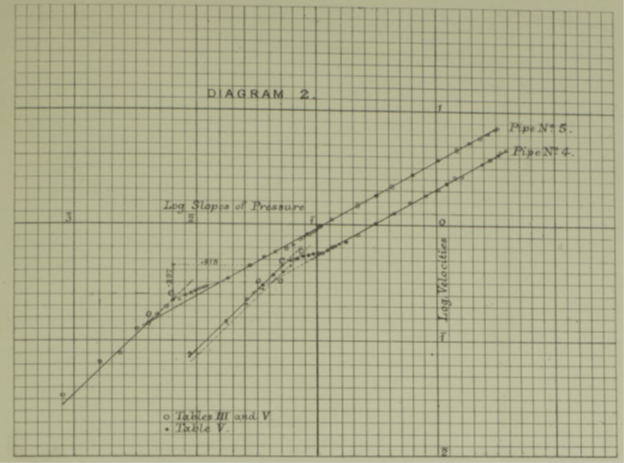
Сразу видно, что кривые очень похожи. А если одну из них перенести на кальку и подвинуть бумагу, чтобы они наложились друг на друга, то они совпадут в точности. При этом бумагу не нужно вращать, а только двигать.

Необходимый горизонтальный сдвиг составляет .913, а вертикальный .294, и это совпадает с разностями логарифмов D³/P² и D/P для этих трубок в пределах точности измерений.

37. Универсальный закон сопротивления в каналах.

Совпадение логарифмических кривых означает, что не только для критической скорости, а для всех скоростей в этих трубках справедливо следующее. Если установить давления такие, что параметр D³i/μ­² одинаковым, то реализуются такие скорости, что будет одинаковым параметр Dv/μ. Другими словами, если i и v для каждой трубки умножить соответственно на D³/μ­² и D/μ, и построить кривые для таких приведённых значений, то кривые совпадут.

В более общем виде: если i = F(v) – это связь между i и v для трубки, у которой D=1, T=0, P=1, то D^3­i/P² = F (Dv/P) – это аналогичная связь  для любой другой трубки, и любого режима течения воды в ней.

До проведения экспериментов даже не предполагалось, что существует настолько универсальная связь между режимом и параметрами течения.

Она была найдена именно благодаря логарифмическому представлению, в котором её нельзя было не увидеть. Но это ещё не всё.

Изначально я не собирался в очередной раз исследовать сопротивления закон трубок при скоростях выше критической. Дело в том, что есть много экспериментальных данных по этой теме, из которых, казалось бы, следует, что этот закон или очень сложный или вообще не существует. Это говорит в пользу гипотезы о том, что за критической точкой сопротивление определяется вихрями, о поведении которых мы мало что знаем. Однако я счёл себя обязанным продолжить эксперименты в более широком диапазоне давлений и скоростей. Я думаю, это самый широкий на сегодняшний день диапазон, реализованный в одной трубке.

Далее мы увидим, что в большой трубке давление в последнем эксперименте в четыре тысячи раз больше, чем в первом. Работая в таком широком диапазоне, я ожидал получить то же, что в более ранних экспериментах: в одной и той же трубке при маленьких давлениях давление пропорционально скорости, а при больших – её квадрату. В этом случае нижний участок логарифмической кривой до критической точки должен быть прямой линией с наклоном 45°, а остальной участок – прямой линией с вдвое меньшим наклоном, т.е. два по горизонтали к одному по вертикали.

Полученные точки на нижних частях кривых лежали вокруг линии с наклоном 45° с некоторым разбросом. Как я уже говорил, это позволило мне предположить, что при низких скоростях поток имеет повышенную температуру, и нужно провести дополнительную серию экспериментов. Некоторые из них приведены в таблице IV. В этой серии  температура была тоже непостоянна, но она значительно отличалась от того, что было раньше. После этого отклонения точек от линии с наклоном 45° можно было объяснить непостоянством температуры и считать, что оно лежит в пределах точности эксперимента.

Но когда были построены в логарифмическом виде верхние участки кривых, они оказались в высшей степени прямыми и параллельными.

Было несколько расхождений, которые нельзя было объяснить температурой, потому что при таком большом расходе воды она была практически постоянна. Оказалось, что они объясняются датчиком расхода. Дело в том, что расход зависит от высоты столба не в точности как его корень. Однако то, как обрабатывались разные комбинации отверстий, исключало возможность систематической погрешности. Средние показания датчика были правильными, поэтому погрешности были локальными, и к тому же, небольшими.

Стало ясно, что какой бы ни был наклон линий, они выражают связь скорости и давления для обеих трубок. А так как они параллельны, то закон не зависит от диаметра трубки. После тщательного анализа было получен наклон 1.723 к 1, что явно отличается от 2 к 1. Таким образом, в диапазоне от 1 до 50 давление ведёт себя как i ~ v^1.723.

Это отличается от результатов предшественников, которые придерживались i = v² или i = Av + Bv². Ни тот, ни другой вариант не описывает результаты данных экспериментов, так как в первом случае получаем наклон 2 к 1, а во втором –  кривую линию. Прямая линия в логарифмическом виде с наклоном 1.723 к 1 может описываться только законом вида i ~ v^1.723.

Поэтому мне было несколько затруднительно приводить закон, полученный по моим экспериментам в однотипных трубках, к виду, удобному для практики. Как уже говорилось, это просто D³i/P² = f ( Dv/P ), где f такова, что x = f(y) – уравнение для кривой, которая описывает зависимость сопротивления от скорости в канале диаметром 1 при нулевой температуре.

Точный вид f сложен из-за области непосредственно за критической точкой.

До критической точки A_cD³i/P² = B_cDv/P.

За критической точкой закон сложен, пока скорость не достигнет значения 1.325v­_c. После этого, как показало логарифмическое представление, кривая опять принимает простой вид AD³i/P² = (BDv/P)^1.723, то есть прямая линия с наклоном 1.723 к 1.

На диаграмме 2 видно, что если продолжить два прямых участка зависимости, они пересекаются не в критической точке. В логарифмическом виде пересечение находится от неё на расстоянии 0.154 как по абсциссе, так и по ординате.

Обозначим точку пересечения o. Тогда

Log (D³i_c/P²) = Log (D³i_o/P²) + 0.154,

Log (Dv_c/P) = Log (Dv_o/P) + 0.154.

Обозначим A = P²/(D³i₀), B = P/(Dv₀), тогд.

Log(A) = Log(A_c) + 0.154,

Log(B) = Log(B_c) + 0.154.

Значения A_c и B_c были получены ранее в разделе 33. Тогд.

Log(A) = 8.8311, A = 67,700,000,

Log(B) = 2.598, B = 396.3 .

Тогда для верхних участков кривых получае.

AD³i/P² = (BDv/P)^1.723.

Пусть n принимает значение 1, если правый или левый член в этом уравнении меньше единицы, и значение 1.722 в противном случае. Тогда AD³i/P² = (BDv/P)ⁿ  – это уравнение для обоих прямых участков зависимости, пересекающихся в точке o, то есть закон сопротивления кроме окрестности критической точки, хотя она встречается на практике.

Если выразить n как разрывную функцию B_cDv/P, то уравнение описывает всю зависимость.

38. Влияние температуры.

Несмотря на то, что диапазон изменения температуры невелик, но по таблицам III и IV видно, что критическая точка смещается. При 9°C log(P^-1) = 0.12093, а при 5°C log(P^-1) = 0.06963, разница 0.05130. Такая же разница должна быть для log(v_c); по таблицам она составляет 0.062. log(i_c) должен меняться как P², то есть на 0.10620, тогда как по таблицам 0.121 .

Погрешность соответствует диапазону температуры примерно 1°C, что вполне допустимо.

Желательно провести эксперименты при более высоких температурах, но это связано с большими трудностями, поэтому я пока их отложил.

IV Сравнение с экспериментами Дарси

39. Эксперименты Дарси.

Закон сопротивления получался по моим экспериментам таким однозначным, что я был вынужден сравнить его с результатами предшественников, хотя изначально это не предполагалось.

При низких скоростях, до критической точки, закон в точности совпадает с формулой Пуазейля (см. раздел 35).

За критической точкой наиболее важными являются эксперименты Дарси, которые признаны Академией Наук и опубликованы в 1845-ом году. Именно на них основана широко используемая формула. Несмотря на то, что она в принципе не могла описывать мои результаты, можно было сравнить его экспериментальные данные с моим законом, что и было проделано.

Это было сравнительно легко, так как эксперименты Дарси подробно задокументированы.

Всего он использовал 22 трубки, диаметром от 0.0014 (такой же, как у самой большой  моей трубки) до 0.5 м. Исследовались трубки следующих видов: свинцовые, стеклянные, сварные железные газовые трубы, полированные железные трубы, старые ржавые и новые чугунные трубы.

Методика экспериментов отличалась от моей только размеров трубок и расстоянием между замерными отверстиями (50 метров у него и 1.5 метра у меня). Из-за такого большого расстояния в трубках Дарси были стыки между замерными отверстиями, да и сами трубки были не очень постоянного диаметра. Эксперименты проведены очень аккуратно, и очень подробно задокументированы, но из-за непостоянства диаметра, доходившего до 10%, и неровности на стыках, эти данные вряд ли будут хорошо описываться законом для трубок с постоянным диаметром. Далее, Дарси мало внимания уделял температуре. Хотя он во многих случаях приводит её, при анализе результатов она не учитывалась, тогда, как по приведённым данным она изменялась в диапазоне 20°C. К тому же, его трубки имели длину 300 метров и находились на открытом воздухе, поэтому были подвержены влиянию солнца.

Дарси предусмотрительно дублировал измерения на двух 50-ти метровых участках, но показания датчиков давления далеко не всегда были непротиворечивы. Вероятно, это связано с вышеуказанными факторами. Особенно сильно это проявлялось при низких скоростях. Расхождение часто составляло 10–15%, и могло доходить до 15 к 7. При обработке данных для таблицы показания осреднялись.

Учитывая это, я не мог ожидать хорошего совпадения с моими данными. Однако эксперименты с такими большими диаметрами вряд ли кто-то повторит, во всяком случае, так же аккуратно и убедительно. Поэтому это была единственная возможность проверить универсальность моего закона.

40. Обработка результатов эксперимента.

Я не рассматривал эксперименты в ржавых и шероховатых трубках, и выбрал свинцовые, полированные, стеклянные и новые чугунные трубки. Их диаметры лежали в диапазоне от 12 до 508 мм. Я построил данные для них в логарифмическом виде на диаграмме 3.

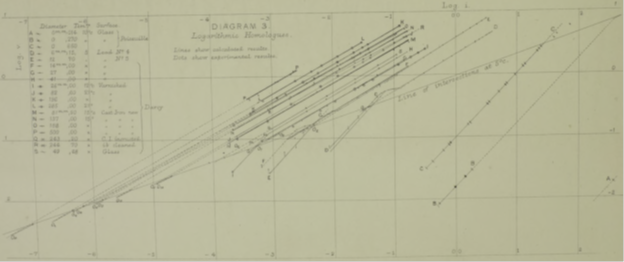
Для двух самых маленьких трубок минимальная реализованная скорость значительно ниже критической. Для некоторых других трубок она близка к ней, поэтому нижние концы этих зависимостей искривлены. В остальных случаях зависимости практически прямые. Некоторые слегка отклоняются в ту или другую сторону, но не более чем из-за  погрешности эксперимента.

Наклон верхних участков для свинцовой и полированной трубок составляет 1.746, что немного выше, чем у меня. Но для стекла и чугуна наклон составляет 1.82 и 1.92 соответственно.

Логарифмическое представление очень информативно, однако главный вопрос в том, согласуются ли зависимости с формулой AD³i/P² = (BDv/P)ⁿ.

41. Сравнение с законом сопротивления.

При проведении этого теста я сначала не смог найти температуру для некоторых экспериментов, а для тех случаев, когда она приводилась, было непонятно, является ли она именно температурой воды между замерными отверстиями.

Но значения температур удалось до некоторой степени восстановить по датам экспериментов и приведённым температурам.

Используя восстановленные значения, для каждой трубки были посчитаны значения  i₀=P²/(AD³) и v₀=P/(BD). Значения A и B приведены выше, а log i₀ и v₀ – координаты точки O пересечения прямых участков логарифмической зависимости. Тогда применимость формулы к экспериментальным данным можно проверить, если продлить верхние участки зависимостей влево – они должны пройти через соответствующую точку O.

Как видно на диаграмме III, согласование очень хорошее. Небольшие расхождения можно объяснить погрешностями, особенно в температуре.

42. Влияние температуры за критической точкой.

Отметим очень важный факт, как с физической, так и с практической точки зрения.  При низких скоростях температура жидкости очень сильно влияет на расход: при 45° C он вдвое больше, чем при 5° C при прочих равных. Однако для больших скоростей влияние очень мало – ни Дарси, ни другие экспериментаторы его вообще не заметили.

В моих экспериментах при больших скоростях температура была постоянной: 5° C. Поэтому этот вопрос не возникал, пока я не начал анализировать результаты Дарси и пытаться восстановить (с большим трудом) значения температур. Тогда я заметил, что изменение температуры сдвигает кривые в направлении 2 по горизонтали к 1 по вертикали. Но это очень близко к наклону кривых при больших скоростях, поэтому изменение от 5 до 10° C практически не изменяло кривую. Другими словами, закон сопротивления при больших скоростях практически не зависит от температуры, то есть вязкости.

Таким образом, с ростом вязкости не только уменьшается критическая скорость, при которой возникают вихри. После их возникновения сопротивление почти не зависит от вязкости, или совсем не зависит.

43. Наклон логарифмических кривых.

Итак, согласование логарифмических кривых однозначно устанавливает связь между диаметром трубки, давлением и скоростью для свинцовых, полированных, стеклянных и чугунных трубок. Однако соотношения между давлением и скоростью для разных материалов трубок отличаются. В логарифмическом представлении это хорошо видно по небольшому, но чёткому отличию в наклоне кривых при больших скоростях.

Так как были исследованы довольно разные трубки, то причин у этого расхождения может быть немного. Это не может быть разница в диаметре, так как по крайней мере три трубки с очень разными диаметрами дали один и тот же наклон. Это не может быть температура. Остаётся лишь одно объяснение различия в n – стыки в трубках и свойства их поверхности.

Это подтверждается тем, что три свинцовые трубки Дарси дают слегка разные значения n, а две мои без стыков дают в точности одно и то же значение, которое немного меньше, чем у Дарси.

Во всех трубках Дарси между замерными точками были неровности. В случае стекла и чугуна сечение менялось до 20%. Наиболее однородными были свинцовые, поэтому гипотеза о том, что разница в значении n вызвана неровностью, имеет право на существование.

44. Описание диаграммы 3.

На диаграмме приводится сравнение экспериментов данной работы с экспериментами Пуазейля и Дарси.

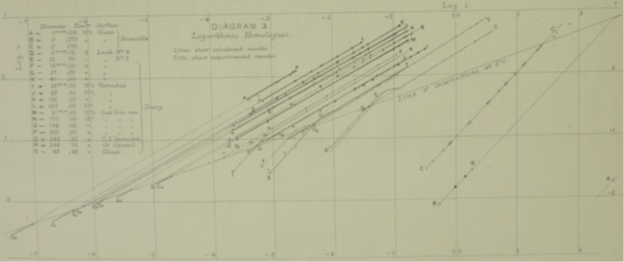
На диаграмме много линий, и её смысл сразу не очевиден. Каждый ряд точек на ней – это экспериментальные данные для некоторой трубки в логарифмическом виде, построенные точно так же, как для диаграммы 2. DD и EE – повторение данных для трубок 4 и 5 в уменьшенном масштабе.

По диаграмме 3 сразу видно, что большая часть данных лежит значительно ниже или значительно выше критических значений. В маленьких трубках Пуазейля реализовались скорости много меньше критических значений, поэтому они имеют наклон 45°.

Минимальный диаметр трубок Пуазейля 0.014 мм. На диаграмме приведена только одна точка из эксперимента, обозначенного как “A”, так как остальные лежат вне диапазона диаграммы. Однако они в точности ложатся на пунктирную линию, проходящую через эту точку, и не достигают критического значения.

Это справедливо для всех его экспериментов, кроме трубки с максимальным диаметром (0.65 мм), поэтому достаточно одной линии, которая обозначена как “BB”.

“CC” – это эксперименты в трубке диаметром 0.65 мм. Они достигают критического значения в соответствии с формулой, и затем отклоняются от прямой линии.

Нужно отметить, что эти точки взяты не непосредственно по данным Пуазейля. Они нуждались в корректировке, так как он измерял сопротивление не по замерным отверстиям, а по давлениям во входной и выходной ёмкостях. Поэтому его значения сопротивления включают в себя как сопротивление трубки, так и давление, необходимое для приведения воды в движение. На это ранее не обращалось внимания, но многие его результаты нужно рассматривать с учётом этого факта.  

В поисках границ применения своего закона Пуазейлю удалось достичь скоростей, при которой он нарушался. Это получилось только в самой большой из его трубок. Когда я изучал его эксперименты, я рассчитывал, что эти скорости будут больше, чем даёт моя формула. Однако они во всех случаях оказались значительно меньше. Тогда я понял, что Пуазейль не учитывал давление, необходимое для движения воды.

Далее нужно было понять, насколько это может объяснить расхождения.

Для не слишком маленьких трубок давление, необходимое для приведения воды в движение, составляет v²/(2g), если на входе установлена воронка, и 1.505v²/(2g), если вход просто цилиндрический. Пуазейль говорит, что тщательно следил за тем, чтобы концы его трубок были цилиндрическими. Поэтому приводимые им давления нужно рассматривать как 1.505v²/(2g), если сравнивать их с данными по трубкам с воронкой.

После такой корректировки получилось, что его закон справедлив для всех маленьких трубок в его экспериментах. А данные для большой трубки согласуются с ним лишь до критического значения, а затем отклоняются, в полном соответствии с моей формулой, как видно по линии “CC”.

Данные Дарси для трубок F, G, I лежат как ниже, так и выше критического значения и очень хорошо согласуются с теорией для обеих ветвей зависимости.

Однако это нужно рассматривать как случайное совпадение, так как при низких скоростях Дарси работал на пределе чувствительности датчиков давления; так, для эксперимента “F” показания датчиков составляли 7 и 15, и осреднялись. Во всех экспериментах есть тенденция к разбросу в нижних точках, и систематическое отклонение от точек, расположенных посредине, что можно объяснить той же причиной.

Вероятно, по той же причине выпадают одна или две верхние точки, так как здесь тоже показания датчиков сильно отличались.

Поэтому для определения наклона теоретических линий в основном использовались промежуточные точки.

Средние наклоны для разных типов трубок составили:

Для экспериментов, в которых была задокументирована температура, т.е. “I”, “J”, “L”, “M”, “N”, точки “O” определялись по формула.

Log i₀ = 2logP – 3logD – 7.851.

Log v₀ = logP – logD – 2.598.

Затем через эти точки были проведены линии с соответствующим наклоном, которые хорошо совпали с экспериментом.

Для экспериментов, в которых температура была не известна, для расчёта log i₀ и log v₀ она была принята 5° C. Эти точки лежат вдоль линии, обозначенной как “line of intersections at 5°”. Через них проведены сплошные линии с наклоном 2 к 1, так как точка “O” должна лежать на них при любой температуре. Штриховые кривые, аппроксимирующие экспериментальные точки, продолжены до пересечения со сплошными линиями. По этому пересечению можно определить реальную температуру. Так как температура слабо влияет на верхние участки зависимости, то это хорошая оценка для неё. Исключение составляют случаи “G”, “H” и “S”, когда пересечение оказалось выше линии для 5° C. Весьма вероятно, что эффективные диаметры трубок в этих случаях были определены с небольшой погрешностью, 2–3%.

Скорее всего, шероховатость трубки, например, в виде накипи или стыков, влияет на логарифмические зависимости. Поэтому рассматривались только наиболее гладкие трубки. Но для проверки этого были нанесены зависимости “Q” и “R”, которые соответствуют трубке с накипью до и после очистки. Их сравнение показывает, что в этом случае накипь влияет только через уменьшение диаметра трубки, а также увеличивает значение n до 2. Отметим, что это была большая трубка, и скорость была значительно больше критической, поэтому вполне возможно в маленькой трубке такая же накипь будет работать по-другому.

Главный вывод, который можно сделать из диаграммы: в диапазоне диаметров 0.000014–0.5 м и перепадов давлений 1–700,000 различие расчётных и измеренных скоростей не превышает 10%, а в основном составляет 2–3%, и систематическое расхождение отсутствует.