III Определение критической скорости по измерениям сопротивления
24.
На первый взгляд такие эксперименты кажутся достаточно простыми. Но если задуматься о способах и средствах их проведения, возникает столько трудностей и погрешностей, что я собрался для этого с духом лишь спустя два года после экспериментов с цветными полосками. Эти два года я занимался гидродинамическим аспектом явления, о чём уже говорилось в разделе 13. Эксперименты с цветными полосками показали, что если вода практически спокойна перед втеканием в трубку, то существует критическое значение скорости, при котором начинают появляться вихри. Также они показали, что при этой скорости вода в трубке очень неустойчива. При наличии же сколько-нибудь заметного начального возмущения распад происходит при значительно меньших скоростях, чем в спокойной воде. Это означает, что если существует такая скорость, при которой вода устойчива к любым возмущениям, то она гораздо меньше, чем скорость, при которой вода становится неустойчивой к бесконечно малым возмущениям. То есть, есть два значения для критической скорости в трубке – одно, когда устойчивое движение превращается в вихри, и другое, когда вихри превращаются в устойчивое движение.
Несмотря на то, что закон для критического значения скорости получается из уравнений движения, как я уже говорил, только в начале этого года мне удалось получить теоретическое объяснение наличия двух критических скоростей. После этого мне стало ясно, что если в достаточно длинной трубке вода изначально сильно возмущена, то ниже по течению она придёт в одно из двух стабильных состояний – или вихри, или устойчивое движение, в зависимости от того, превышает ли скорость некое значение, которое можно назвать настоящим критическим значением.
Так как было нужно вносить начальные возмущения, то методика цветных полос не подходила. Оставалось только измерять сопротивление хвостовой части трубки одновременно с расходом.
Изменение закона сопротивления можно было установить только в серии экспериментов, которые проводятся в одних условиях, то есть температура, состав воды и состояние трубки. Кроме того, диапазон скоростей должен охватывать большую окрестность критического значения. Для этого было решено брать воду из Манчестерского водопровода, используя давление в нём как движущую силу. Эксперименты проводились в мастерских колледжа Оуэнса, с использованием имеющегося там оборудования для подачи и измерений воды для экспериментальных турбин.
25. Экспериментальная установка.
Она показана на рисунке 17.
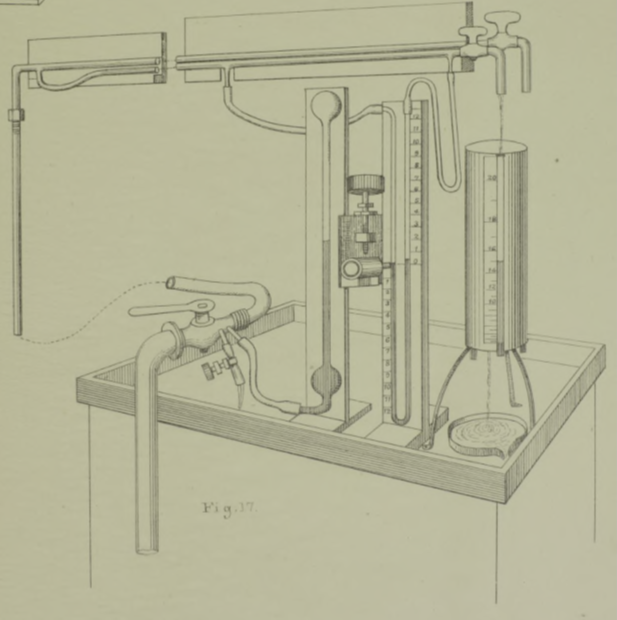
Искомое критическое значение должно было быть значительно меньше, чем для превращения стационарного движения в вихри. Поэтом для большой трубки (трубка №5) был выбран диаметр 12 мм, а для маленькой (трубка №4) – 6 мм. В предыдущих экспериментах две маленькие трубки были примерно такого же диаметра.
Это были обычные свинцовые трубки для газа или воды. Технология их производства такова, что у них очень постоянный диаметр, и у новых трубок внутренняя поверхность очень гладкая, поэтому они хорошо подходили для наших целей.
Длина трубок 4.8 метра. Они помещались в жёлоб, состоящий из двух дюймовых досок под прямым углом. Затем жёлоб фиксировался так, что одна его сторона была вертикальной, а другая – горизонтальной. Таким образом, трубки лежали на горизонтальной полке, на высоте 2.1 метра от пола. Для управления расходом на выходе из трубок были установлены краны. На входе они соединялись с резиновым шлангом, в свою очередь подключённым через Т-образный патрубок к водопроводу. Это было специально сделано для того, чтобы создать большие возмущения на входе в трубки. Шланг соединялся со 100-миллиметровой водопроводной трубой 6-миллиметровым краном. Таким образом, давление на входе в трубки регулировалось этим краном, а расход регулировался концевыми кранами.
Такая двойная регулировка была необходима из-за того, что давление в водопроводе менялось. Более того, после предварительных экспериментов был добавлен третий, более чувствительный управляющий элемент, а также датчик давления, с тем, чтобы в ходе эксперимента поддерживать постоянное давление в шланге, т.е. на входе в трубки.
Управляющий элемент был устроен следующим образом. Между шлангом и водопроводным краном были установлены два коротких патрубка. На конце одного из них был установлен резиновый насадок с хомутом, так, чтобы часть воды, прошедшей через кран, могла выливаться. Другой соединялся с нижним концом вертикальной стеклянной трубки диаметром около 6 мм и длиной 750 мм. Возле нижнего конца эта трубка имела шаровую фирму диаметром около 50 мм. Верхний её конец тоже был такой формы, как показано на рисунке.
Это устройство работало как довольно чувствительный датчик давления. Приходящая снизу вода вытесняла воздух из нижнего шарика в верхний, создавая давление около 750 мм. рт. ст. Избыточное давление компенсировалось как сжатием воздуха в верхнем шарике, так и весом воды в трубке. В ходе эксперимента хомут непрерывно подстраивался так, чтобы уровень воды между шариками оставался постоянным.
26. Датчики сопротивления.
Для измерения сопротивления использовались только последние 1.5 метра трубки. Первые 3 метра предназначались для установления потока.
Достаточно ли трёх метров для установления потока? Если измерять в диаметрах, это расстояние для малой трубки вдвое больше, чем для большой. Если бы этого расстояния было недостаточно, то для большой трубки мы получили бы менее систематические результаты, чем для малой. Однако этого не произошло, поэтому можно считать это расстояние достаточным.
Чтобы измерять давление в двух точках, в каждой трубке были просверлены два отверстия – непосредственно возле конца и на расстоянии 1.5 метра перед ним. Диаметр отверстий около 1 мм. Так как вода в области этих отверстий движется быстро, любая шероховатость или заусенцы, образовавшиеся при сверлении, могли искажать измерения. Было очень важно этого избежать. Если просто просверлить отверстие снаружи, то непонятно как убирать появившиеся заусенцы внутри трубки, так как она тонкая, а отверстие находится на расстоянии 1.5 метра от её конца. Но мистер Фостер нашёл выход – просверлить трубку насквозь, а потом заткнуть входное отверстие. Действительно в этом случае заусенцы получались очень маленькими, в чём мы убедились.
Перед сверлением к трубкам были припаяны короткие патрубки, с которыми должны были сообщаться просверленные отверстия. Патрубки через резиновые трубки соединялись с коленами сифонного манометра.
Колена манометра были длиной около 0.75 метра. Он представлял собой U-образную стеклянную трубку, то есть колена были параллельны, и отстояли друг от друга примерно на 25 мм. Манометр работал в двух вариантах – в одном случае в нём находилась ртуть, в другом – сероуглерод.
Стеклянные трубки редко имеют постоянный диаметр по длине; размер колен также отличался, что важно при использовании сероуглерода.
Трубки были зафиксированы на стойке с проградуированной шкалой, так, чтобы можно было определить высоту столба ртути или сероуглерода. Предполагалось, что такой точности будет достаточно. Но оказалось, что желательно измерять с точностью 1/40 мм.
Поэтому был использован своего рода катетометр, который был сделан для моих экспериментов по транспирации, и обеспечивал определение границы раздела двух жидкостей с точностью 1/400 мм.
Вода непосредственно контактировала с жидкостью в сифоне, для этого воздух удалялся с помощью резиновых соединений.
27. Методика измерения расхода.
По многим причинам было очень желательно измерять расход за минимально короткое время.
Для этого было изготовлено некое подобие водослива. Вертикальный жестяной цилиндр глубиной 0.6 метра с плоским дном, на котором располагалась диафрагма из большого количества слоёв тонкой проволочной сетки толщиной 50 мм. Трубка соединялась с дном через вертикальную стеклянную трубку, высота столба воды в которой определялась давлением воды под сеткой. Сзади неё находилась шкала, деления которой соответствовали квадратам высоты. В тонком жестяном дне были просверлены шесть отверстий: одно диаметром 3 мм, одно 6 мм и четыре по 12 мм.
Отверстия закрывались пробками, так что можно было использовать любое отверстие или любую комбинацию.
Мы использовали следующие комбинации:
№ 1. Отверстие 3 мм.
№ 2. Отверстие 6 мм.
№ 3. Отверстие 12 мм.
№ 4. Два отверстия 12 мм.
№ 5. Четыре отверстия 12 мм.
Опыт показывает, что скорость вытекания воды из сосуда через круглое отверстие в тонкой горизонтальной пластине практически пропорционально площади отверстия и корню из давления. Поэтому для выбранного отверстия относительное значение расхода можно определить по высоте столба воды в трубке. Показания прибора были верифицированы по времени заполнения сосудов известного объёма. Таким образом, были получены коэффициенты для каждой из комбинаций 1, 2, 3, 4 и 5.
Таблица II.
|
№ комбинации |
Показания прибора |
Время, сек. |
Объём, мл |
Коэффициент |
Логарифмический коэффициент |
От переводчика: остаток таблицы с численными данными можно найти в первоисточнике.
Из таблицы видно, что абсолютные значения коэффициентов получены из экспериментов с комбинациями 1 и 2, а коэффициенты для комбинаций 3, 4 и 5 получены по сравнению с временем заполнения сосуда неопределённой ёмкости, которое обозначено в таблице как A. Относительные значения коэффициентов практически пропорциональны квадратам диаметров отверстий.
Для маленьких скоростей комбинация № 1 оказалась слишком большой, и, чтобы не задерживать эксперимент, были задействованы две стеклянные колбы: колба 1 и колба 2. Расход измерялся по времени их заполнения, и равнялся отношению объёма ко времени заполнения. Их объём по измерениям постфактум составил 303 и 1160 мл.
28. Методика экспериментов.
Она состояла в следующем: мой ассистент, мистер Фостер, обеспечивал подачу воды из водопровода и следил, чтобы уровень воды в датчике давления не менялся.
Выходной кран на трубке закрывался, и снимались нулевые показания прибора; при этом микрометр настраивался на границу воды и жидкости в левом колене датчика. Затем винт микрометра поворачивали на один полный оборот, от чего его перекрестие опускалось на 1.7 мм. После этого кран на конце трубки регулировался так, чтобы жидкость в датчике опустилась к перекрестию. Убедившись, что процесс установился, измерялся расход.
После этого микрометр опускали ещё на один оборот винта, снова подстраивали кран, и так далее примерно 20 раз, что соответствует перепаду в датчике около 12 мм. Далее измерения проводились через каждые пять оборотов винта, до достижения предела, примерно 50 мм. После этого показания снимались просто по наблюдениям за шкалой. По-хорошему, при этом нужно было фиксировать уровень ртути или сероуглерода в обоих коленах датчика, но это делалось не всегда. В некоторых случаях фиксировался уровень только в одном колене, при этом в протоколах указывалось, в каком именно.
В таблицах III, IV и V приведены результаты, а буквы r, l и b означают “правое колено”, “левое колено” и “сумма правого и левого”.
При использовании ртутного манометра обнаружилось, что когда ртуть в левом колене опускалась на 39 делений, ртуть в правом колене поднималась на 41 деление. Поэтому для получения суммы этих показаний, показания левого колена надо умножать на 2.05, а правого – на 1.95.
При использовании сероуглерода 11 делений слева соответствовали 9-ти делениям справа, поэтому коэффициент для левого колена составил 1.8, а для правого 2.2.
29. Сравнение датчиков давления.
Показания датчиков давления приводились к одной системе единиц путём их сопоставления. Так, 0.25 на левом колене ртутного датчика соответствовало 24-м дюймам на обоих коленах сероуглерода. Следовательно, чтобы привести показания сероуглеродного датчика к показаниям ртутного, нужно их умножить на 0.25×2.05/24=0.0213.
Таким образом, показания переводились в единую систему единиц, т.е. 1/1000 дюйма ртутного столба. После этого они умножались ещё на 0.00032 для перевода в метры водного столба.
Из соображений сравнения удобно работать с перепадом давления на единицу длины. Для этого давление в метрах водного столба делились на 1.524, т.е. расстояние в метрах между отверстиями датчиков. Эти данные приведены в таблицах в столбцах под буквой i.
Расход, измеренный разными комбинациями отверстий, пересчитывался в кубические сантиметры. Если поделить его на площадь сечения трубки, получаем среднюю скорость потока воды.
30. Площади и диаметры трубок.
Для определения площадей были измерены диаметры путём подгонки под трубки латунных пробок и последующего измерения диаметров этих пробок. Диаметры трубок 4 и 5 составили 6.15 и 12.7 мм, а площади 29.7 и 125 мм2 соответственно.
Расход в кубических сантиметрах, отнесённый к сечению в квадратных миллиметрах, даёт среднюю скорость, приведённую в таблицах III, IV и V.
Для сравнения приведены также логарифмы i и v.
31. Температура.
Основная причина, почему использовалась вода именно из водопровода, в том, что она имеет постоянную температуру. По моему опыту, она может оставаться постоянной неделями.
Перед началом экспериментов вода, свободно вытекающая из водопровода, имела температуру 5°C. Это значение сохранялось до конца экспериментов. Однако мы не предполагали, что температура воды в трубке подвержена изменениям, которые к тому же сложно отследить.
Это обнаружилось только в ходе обработки результатов экспериментов. Дело в том, что температура в помещении была выше, чем в водопроводе, за счёт чего вода нагревалась, пока текла по трубке. Степень нагрева зависела от характера течения. Предвидя это, мы провели предварительные эксперименты, по результатам которых нагрев составил менее полградуса. Поэтому в ходе основных экспериментов предполагалось, что им можно пренебречь. Однако при обработке выяснилось, что для маленьких расходов в разных экспериментах получаются слишком большие разбросы по скорости. Это заставило снова вспомнить о температуре.
При таком объяснении, разбросы выглядели не столь серьёзными. Нужно было только аккуратно повторить все эксперименты при низких скоростях, измеряя температуру вытекающей воды, что и было проделано, а также проведены дополнительные эксперименты (см. раздел 33).
Таблица III.
Эксперименты по сопротивлению трубок 29 января 1883.
Трубка №4, свинец, диаметр по измерениям 6.15 мм. Длина 6.4 м, первое отверстие на расстоянии 3.84 м, между отверстиями 1.524 м. Вода из Манчестерского водопровода.
|
№ п/п |
Давления |
Расходы |
Температура |
Перепад давления воды, i |
Скорость v, м/с |
log i |
log v |
|
|||||||
|
|
Ртуть, дюймы воды
|
Сероуглерод, дюймы воды
|
м. вод. ст.
|
Время заполнения ёмкости, сек. |
Скорость истечения из донного отверстия |
см/сек. |
°C
|
°F
|
|
|
|
|
|
||
|
1. 303 мл |
2. 1160 мл и т.д. |
Комбинация 1. |
Комбинация 2. и т.д. |
||||||||||||
Таблица IV.
Те же условия, что для таблицы III, кроме температур при низких скоростях.
Таблица V.
Трубка №5, свинец, диаметр по измерениям 12.7 мм. Длина 6.4 м, первое отверстие на расстоянии 3.84 м, между отверстиями 1.524 м. Вода из Манчестерского водопровода.
От переводчика: таблицы с численными данными можно найти в первоисточнике.
32. Результаты экспериментов.
Было проведено большое число предварительных экспериментов, прежде чем результаты стали внутренне непротиворечивыми. После этого для каждой трубки был последовательно проведена вся программа экспериментов. Их результаты приведены в таблицах III и V.
33. Критические скорости.
Определение критических скоростей было основной целью экспериментов, и в какой-то степени осуществлялось прямо в ходе их проведения. Если начинать с минимальных скоростей, то сначала жидкость в датчике перепада давления очень спокойна, и её уровень монотонно снижается с ростом скорости. Но в какой-то момент датчик как будто бы начинает работать неправильно. Жидкость начинает подпрыгивать, и при малейшем повороте крана, регулирующего скорость, она уходит из поля зрения микроскопа. Сначала каждый такой случай был для меня неожиданностью, но повторив эксперименты несколько раз, я точно знал, когда это произойдёт. Появление такой нестабильности отмечено в таблицах.
Однако критические скорости определялись не по появлению нестационарности в датчике давления, а по сопоставлению отношений скоростей и давлений, которые приведены в таблицах в столбцах v и i. Это сравнение приведено на диаграмме I, где i – абсцисса, v – ордината.
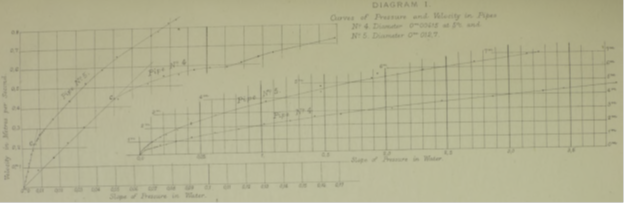
Видно, что для обеих трубок экспериментальные точки лежат практически на прямой линии до некоторой точки, названной C, после которой быстро от неё отклоняются. Эти точки соответствуют экспериментам № 6 и 59, которые в таблице находятся как раз над экспериментами, которые помечены как нестационарные.
Таким образом, для определения критических скоростей можно использовать как изменение в законе давления, так и появление нестационарности.
Я предположил, что прямизна кривых между началом координат и критической точкой должна зависеть от постоянства температуры. Именно благодаря небольшим отклонениям возникла вышеупомянутая гипотеза о непостоянстве температуры. Это непостоянство подтвердилось в дальнейших экспериментах, некоторые из них приведены в таблице IV. По этим данным, вероятное изменение температуры в таблице III – от 12 до 9°C в критической точке, а в таблице V – от 12 до 8°C. Небольшое отклонение от прямой линии обусловлено этими перепадами.
Остаётся лишь установить, насколько соотносятся полученные значения критической скорости с отношением μ/D или P/D.
Для трубки №4 из таблицы III: D=0.00615м, vc=0.4426м при 9°C; при этой температуре P=0.757 (см. раздел 22). Обозначим Bc=P/(vcD), тогда Bc=279.7 .
Для трубки №5 из таблицы V: D=0.0127, vc=0.2260 при 8°C; при этой температуре P=0.7796 и Bc=272.0 .
Разница в значениях Bc может объясняться отличием температуры в четверть градуса, поэтому результаты вполне лежат в пределах точности экспериментов.
Разумеется, каждой величине критической скорости соответствует критическое значение давления. Его можно найти следующим образом.
Теоретически закон сопротивления для устойчивого движения можно выразить как AcD2i = BcPv; умножим обе части на D/P2, получим AcD2i / P2 = BcD /P × v. Этот закон работает до достижения критической скорости, при которой правая часть обращается в единицу по определению Bc. Тогда Ac= P2/(D3ic). По таблице III ic = 0.0516, P2 = 0.573, D3 = 0.000,000,232, откуда Ac=47,750,000. По таблице V ic = 0.00638, P2 = 0.607, D3 = 0.000,002,05, откуда Ac=46,460,000. Полученные значения Ac отличаются меньше, чем было бы в случае отличия температуры в полградуса.
Следовательно, можно считать доказанным то, что критическая скорость меняется как μ/D.
Продолжение следует.


