Факторизация и эллиптическая кривая. Часть V

К тем сведениям об эллиптических кривых (ЭК), которые доступны читателям Хабра и Интернета в целом, а также из бумажных книг, предлагаю дополнительные, уточняющие важные детали, опущенные в некоторых статьях. Например, в работе приводится изображение тора (рис. 4), но никаких оговорок не делается. Откуда он взялся, почему тор? Другие авторы вообще не упоминают эту фигуру. В чем здесь дело?

Не могу назвать публикацию на Хабре и других сайтах, где автор говорил бы о полях многочленов, хотя обозначение $$) таких полей некоторыми авторами и используются, но делается это неправильно. Неприводимый многочлен и примитивный элемент поля и не задаются, что не позволяет читателю построить такое поле и работать с ним, проверить вычислением приводимый результат, если числовой пример вообще приводится. От таких публикаций остается ощущение зря потраченного времени. Такие поля расширения используются в стандартах цифровой подписи и шифрования рядом государств.

Не буду указывать на явные ошибки, читатели в своих комментариях часто сами их указывают, но сделаю попытку высветить общую картину. Попробую перечислить промахи наиболее распространенные и часто повторяемые многими авторами. Практически не называются допущения и ограничения моделей, которые приводятся в публикациях, особенно, когда модель не авторская, а созданная кем-то другим. Важность границ применимости можно не обсуждать — с этим согласны все, но указывается на это авторами исключительно редко.

Пространства изучения моделей

Здесь будем использовать в зависимости от рассматриваемой ситуации различные пространства вещественные и комплексные, аффинные и проективные, бесконечные и конечные подходящей размерности. Поэтому вначале кратко рассмотрим их сущность основные свойства, способы описания. Для практики фактически наибольший интерес представляет конечный случай.

Аффинные пространства $$

Рассмотрим множество наборов (а1, а2, …, аn) из n элементов, где каждый аi ∊ F и F некоторое поле. Множество наборов обозначим символом $$ и обычным способом введем для наборов операции сложения и умножения на скаляры. При условии замкнутости множества $$по этим операциям оно образует векторное пространство с аддитивным нейтральным элементом О = (0, 0, …, 0).

Для удобства в дальнейшем условимся обозначать набор (а1, а2, …, аn) символами а, в, с…, а $$ будем называть n-мерным аффинным пространством, его элементы – аффинными точками, точку О = (0, 0, …, 0) – назовем началом координат. Если F — конечное поле из $$ элементов, где р – простое, то $$ содержит $$ элементов (наборов, точек). При р = 2 получаем множество всех двоичных чисел разрядности k.

Аффинная плоскость $$

Пусть F˟ – конечное алгебраически замкнутое поле и Fо – некоторое подполе поля F˟. Аффинная плоскость $$ под полем F˟ (дискретная конечная F˟×F˟ ) представляет собой множество всех {(α, β)} упорядоченных пар элементов α, β поля F˟. Каждую такую пару Q=(α, β) называют точкой плоскости $$, а элементы α, β – координатами точки Q. Если поле F˟ является полем расширения некоторой степени n, то каждая координата точки Q представляет собой многочлен степени не выше n – 1 от формальной переменной t.

Эллиптической кривой (ЭК) над полем F называется плоская гладкая кривая с уравнением вида
$$ Индексы у коэффициентов $$ в уравнении указывают степени, которые должны быть приписаны этим коэффициентам, чтобы уравнение ЭК стало однородным, т.е. чтобы каждое слагаемое в нем имело общую степень 6.

Через Е(F) обозначают множество, состоящее из точек $$, удовлетворяющих этому уравнению, с добавлением «бесконечно удаленной» точки О. Если К — некоторое расширение поля F, то через Е(К) будет обозначаться множество, состоящее из точек $$ удовлетворяющих уравнению ЭК и бесконечно удаленной точки О.

Пример 1. Для поля с характеристикой p = 5 и степенью расширения n = 3 задается примитивный элемент (α) и неприводимый многочлен $$ Порядок поля при этом $$, а аффинная плоскость содержит $$ точек с многочленами в роли координат точек.

Например, задание одной из точек эллиптической кривой в этом поле имеет вид $$, где многочлены $$ – координаты точки Q. Малая часть точек такой дискретной плоскости образует ЭК и еще меньшая их часть — является аддитивной группой точек ЭК, которая строится здесь.

Пусть F˟ – алгебраическое замыкание поля поля F. Условие гладкости кривой означает, что в множестве Е(F˟) не существует точек, в которых одновременно обращались бы в нуль частные производные $\$inline\$\partial g(x,y)/\partial x,\; \partial g(x,y)/\partial y,\$inline\$$ где
$$

Иными словами, система уравнений
$$
$$
не имеет решений, принадлежащих Е(F˟).

Проективное пространство $$

Символом $$ по аналогии с предыдущим будем обозначать n-мерное проективное пространство над полем F. Очень важно понимать, как устроено это пространство, и в чем отличие $$ от $$. С этой целью рассмотрим вначале $$– множество наборов (ао, а1, …, аn), в котором точка O=(0, 0, …, 0) – начало координат удалена.

Над множеством $$ определим отношение эквивалентности: n–мерная точка а = (ао, а1, …, аn) эквивалентна точке b = (bо, b1, …, bn), если существует такой элемент γ∊F*, где F* – мультипликативная группа поля F, что aо=γbо, a1=γb1,…,an=γbn. Просто убедиться в том, что все такие пары (a, b) из $$ образуют отношение (~) эквивалентности, которое индуцирует разбиение множества $$ – на классы эквивалентности.

Все такие классы называются точками пространства $$ и все элементы класса (т.е. сам класс) обозначаются символом [а], если точка а = (ао, а1, …, аn) входит в состав класса, то такая точка а называется представителем класса. В геометрической терминологии все элементы (точки) произвольного класса [а] принадлежат прямой в пространстве $$, проходящей через точку а и начало координат в аффинном пространстве.

Пространство $$ образованно $$ элементами (точками). Это легко показать, так как пространство $$ имеет $$ элемент (без нулевого), мультипликативная группа F* поля F˟ состоит из q – 1 элементов (точек проективного пространства). Каждый класс эквивалентности (прямая) порождается произвольным элементом а = (а0, а1, …, аn) умноженным на каждый элемент из F*, т.е. содержит q – 1 элементов.

Тогда число |H˟| классов (их объёмы одинаковы) эквивалентности можно подсчитать по формуле: $$
Сравнение мощностей n–мерных пространств аффинного и проективного показывает, что $$. Тогда $$ – мощность (порядок – число элементов) аффинного пространства $$;
$$ — мощность (порядок) аффинного пространства $$; в нем |H˟| классов. $$ — мощность (порядок) проективного пространства $$, т.е. число классов эквивалентности точек пространства $$. Видим, каждый класс эквивалентности содержит 7 элементов. $$

Наряду с аффинной плоскостью в криптографии с эллиптическими кривыми используется проективная плоскость. Это связано с тем, что для ЭК, задаваемой в этой плоскости, формулы для групповой операции с точками ЭК не содержат действия деления, т.е. для вычисления координат результирующей точки не требуется обращения элемента в поле F, которая весьма трудоемка. Иногда для проективной плоскости используют обозначение $$, чтобы подчеркнуть вещественную природу (некомплексную) элементов.

Определение. Приведем в определении тройственное представление проективной плоскости:
$$= {прямые в $$, проходящие через начало координат} =
= {отношение вида X: Y: Z} =
= { $${0}/~, где (X: Y: Z), (γХ:γY:γZ), если γ∈R}.

В нижней (последней) строчке определения записано фактормножество точек пространства $$ (трехмерного, вещественного) по отношению эквивалентности (~), где γ принадлежит F* -множеству вещественных чисел без нуля, т.е. мультипликативной группе поля.

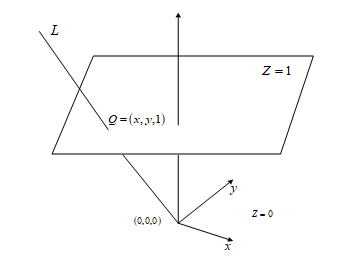
Рисунок 1 – Аффинная плоскость Z = 1

Легко может быть выполнен переход к произвольному векторному пространству над любым полем. Для того, чтобы представить отношение X: Y: Z для Z = 0, достаточно положить x = X/Z,
y = Y/Z. Этим достигается упрощение, так как исходное отношение задается теперь парой вещественных чисел.

Другими словами, класс эквивалентности троек (x, y, z) по отношению эквивалентности имеет единственного представителя (x, y, 1), третья координата которого Z /Z = 1 для всех точек.
К сожалению, Z все-таки может обращаться в нуль, и в этом случае наш способ представителя класса эквивалентности не годится.

Приведенное рассуждение показывает, что $$ содержит экземпляр пространства $$

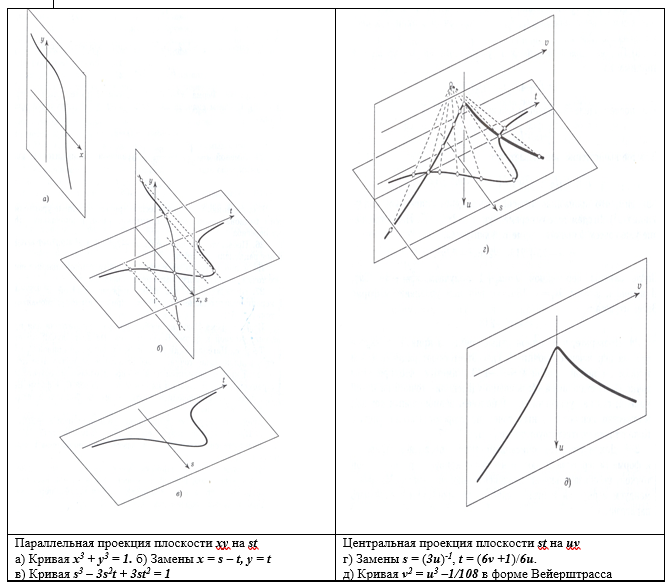
Рисунок 2 – Замены переменных, переводящие кривую в проективное пространство

Прямая общего положения в $$, проходящая через О, не содержится в плоскости (Z = 0) и, значит пересекает плоскость (Z = 1) в единственной точке, которая и представляет собой этот класс эквивалентности (т.е. прямую L в $$). Прямые, лежащие в плоскости (Z = 0), не пересекают плоскость (Z = 1). Следовательно, они соответствуют не точкам из $$ а асимптотическим направлениям или пучкам параллельных прямых в $$. Таким образом, можно представить $$как пространство, состоящее из плоскости $$, к которой добавлено по одной “точке на бесконечности” для каждого пучка параллельных прямых.

Ньютон занимался и кубическими кривыми, привел их классификацию, им сформулирована Теорема. Для любой неособой кубической кривой существует проективная замена координат, преобразующая кубическую кривую к кривой в форме Вейерштрасса с рациональными а и b. Например, m(m+1)/2=n(n+1)(2n+1)/6 после замены m=(у-9)/18 и n=(x-3)/6 получаем уравнение$$ рациональные корни которого и будут решением задачи.

Приведем кривую $$ к форме Вейерштрасса. Выполним проективную замену координат х = s -t, y = t. Эта замена осуществляет параллельную проекцию плоскости ху на плоскость st. Получаем кривую$$. Теперь спроецируем плоскость st на плоскость uv из центра. Еще одна замена координат s=1/3u и t =(6v+1)/6u. Новая кривая (в форме Вейерштрасса) получает вид $$

Вопрос на понимание ЭК: Какие два натуральных смежных числа при умножении у(у+1) равны произведению трех натуральных смежных чисел (х-1)х(х+1)? В уравнении есть $$ как в ЭК.

Формулы групповой операции ЭК в проективном пространстве (плоскости).
Пусть задано уравнение ЭК в проективной плоскости в форме Вейерштрасса Е(GF(q)):
$$
над полем характеристики р, (р ≠ 2 и р ≠ 3), получаемое путем перевода ЭК из аффинной в проективную плоскость. Точки такой ЭК можно рассматривать как эквивалентный класс точек (X, Y, Z) плоскости $$ над полем GF(q).

Бесконечно удаленная точка O ,O ∈ $$ представляет все ненулевые точки с отношением эквивалентности (X, Y, Z) ~(kX, kY, kZ). Такие точки обозначаются как (X, Y, Z) и среди них имеется единственная точка с координатой Z = 0 – это точка (0, 1, 0). При Z = 0 обязательно и Х = 0, и существует только один класс эквивалентности с Х = Z = 0, содержащий бесконечно удаленную точку (0, 1, 0)∈ Е(GF(q))∈ $$.

Существует возможность и обратного перевода ЭК из пространства $$ в аффинное пространство $$. Для всех точек Q = (X, Y, Z) ≠ O производится замена (X, Y, Z) = (Х/Z, Y/Z, 1). При этом выполняется однозначное соответствие: точке (х = Х/Z, y = Y/Z) соответствует точка (X, Y, Z).
Формулы удвоения точки ЭК в проективном пространстве принимают вид:
$$
$$,
где координата $$ кратна λ.

Последующие преобразования обеспечивают получение формул группового сложения точек ЭК в проективных координатах.

Суммирование пары различных точек группы ЭК в проективном пространстве соответствует некоторой третьей точке $$этой группы, имеющей три координаты. Так третьей координатой является $$, а весь набор получает вид

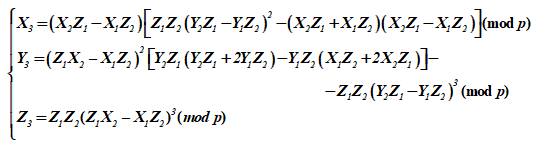
При рассмотрении ЭК над расширенным полем $$, имеющих инвариант j ≠ 0 формулы принимают иной вид для случая $$

Комплексное пространство C

Эллиптическую кривую можно рассматривать не только в аффинном, проективном, но и в комплексном пространствах. В последнем случае точки ЭК называются комплексными точками. Далее будем рассматривать именно такие точки над комплексными полями.

Поскольку ЭК – это плоская кривая, то ограничимся рассмотрением комплексной проективной плоскости $$. В этой плоскости можно задавать функции, которые имеют два линейных независимых периода. Их называют мероморфные двоякопериодические функции с периодами ω1, ω2.

По причине линейной независимости периодов над R, ω1/ω2∈R. Другое название для таких функций – эллиптические функции. Для наших целей интерес представляет функция Вейерштрасса ℘(z), которая удовлетворяет дифференциальному уравнению вида
$$
где $$ – некоторые константы, зависящие от периодов ω1, ω2.

Сходство записанного уравнения с ЭК весьма значительное.
Зададим на плоскости С решетку Λ={mω1 + nω2|m,n∈Z} периодов, где m и n — целые числа и узлы решетки Λ целочисленные. Элементы решетки образуют нормальную подгруппу в группе комплексных чисел, и мы можем сформировать по этой группе факторгруппу C/Λ.

Позднее покажем, что элементы факторгруппы можно отобразить в комплексные точки Е(С) ЭК Е, и такое отображение взаимно однозначно.
Многочлен правой части $$ ЭК над комплексной плоскостью С.
Параметризацию удаётся осуществить для части ЭК на С, благодаря выбору необходимой функции ℘.

В проективной комплексной плоскости с учетом полюсов функции ℘ параметризация устанавливает взаимно однозначное соответствие между множеством точек C/Λ и множеством Е(С) комплексных точек кривой Е. Такое соответствие оказывается биголоморфно.

Суммирование комплексных чисел определяется групповым законом сложения на торе C/Λ. Ниже будет показано, что соответствие φ: C/Λ→Е(С) ЭК Е. Далее выясняется, что любая ЭК на С может быть нормализована подбором подходящей функции Вейерштрасса ℘. В основе процедуры прояснение такой связи лежит возможность обращения эллиптических интегралов.

Эллиптические функции

Определение. Алгебраическую кривую называют эллиптической, если она как одномерное комплексное многообразие представляет собой тор (бублик).
Определение. Мероморфная двоякопериодическая функция называется эллиптической.

Определение. Аналитическая функция называется мероморфной, если у нее в конечной области С нет особых точек, отличных от полюсов.
Определение. Функция:f^C →С∪({∞} называется двоякопериодической с периодами ω1, ω2 при линейной независимости периодов над R и f(z+ω1)=f(z)=f(z+ω2) для любых z∈C.

Двоякопериодическую функцию называют эллиптической, если она мероморфна. Множество эллиптических функций образует поле при фиксированных периодах ω1, ω2. В плоскости С точки 0, ω1, ω2 и ω1+ω2 образуют вершины параллелограмма
П={α1ω1+α2ω2|0 ≤α1,α2 ≤1}, который называется фундаментальным. Стороны, сходящиеся в точке 0 и сама точка принадлежат П, а три другие вершины и две стороны — не принадлежат П.

Особый интерес представляет фундаментальный параллелограмм и его граница.
Определение. Фундаментальным параллелограммом называется область плоскости С, заданная соотношением П ={α1ω1+α2ω2|0 ≤α1,α2 ≤1} где α1,α2∈R.
Параллелограммом периодов называется любой параллелограмм вида α+П, α∈С. Для всех таких параллелограммов справедливы одинаковые условия.

Относительно эллиптических функций Ж. Лиувиллем (1809-1882) сформулированы и доказаны следующие результаты.

Теорема 1. Не существует отличных от констант целых эллиптических функций.
Доказательство. Целая эллиптическая функция непрерывна, так как не имеет полюсов; поэтому она ограничена на замыкании П. В силу периодичности функция ограничена на С, следовательно, она постоянна.

Следствие 2. Две эллиптические функции, имеющие одинаковые наборы полюсов и соответственно равные главные части в полюсах, отличаются на константу.

Теорема 3. Если эллиптическая функция f(z) не имеет полюсов на границе L параллелограмма П+α, то сумма вычетов f(z) во всех полюсах, лежащих внутри П+α, равна 0.

Эллиптическая функция Вейерштрасса. Эта функция играет важную роль для всей теории эллиптических функций в силу ее замечательных свойств. Займемся рассмотрением этих свойств подробнее и выясним, как и какие из них могут быть использованы для наших целей, связанных с изучением ЭК. Функция Вейерштрасса определяется над комплексной плоскостью C и представляется формулой.

,
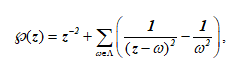
где Λ не содержит точку 0, т.е. решетка периодов с удаленной точкой 0 и фиксированными значениями ω1, ω2. Выражение под знаком суммы нельзя записывать через две суммы, так как каждая из них представляет расходящийся ряд.

Комплексная плоскость C с решеткой Λ

Перейдем к рассмотрению комплексного случая ЭК.
Пусть ω1 и ω2 — два линейно независимых на R комплексных числа. Обозначим через
Λ={nω1 +mω2|n,m ∈ Z} порожденную ими решетку. Отождествим две точки комплексной плоскости С, если их разность принадлежит Λ. После такого отождествления получим фактор-пространство С/Λ.

На рисунке заштрихованная часть комплексной плоскости представляет собой фундаментальную область – параллелограмм, сдвиги которого на элементы из Λ накрывают всю плоскость С.

Рисунок 3. Фундаментальный параллелограмм в комплексной плоскости

Фактор-пространство С/Λ можно представить в виде фундаментального параллелограмма с отождествленными противоположными сторонами. Так как сложение комплексных чисел (x,y) → x+y задает некоторое голоморфное отображение C×C→C, то С является комплексной группой Ли, а Λ – ее подгруппой. Таким образом, фактор-пространство С/Λ – компактная комплексная группа Ли.

Пару (ω1, ω2) можно умножить на комплексное число$$ или $$ и получить пару, состоящую из 1 и τ, где Imτ>0. Соответствующую решетку, порожденную 1 и τ обозначим через Λτ, а фактор-пространство С/Λτ через Eτ. Каждое пространство С/Λ изоморфно одному из Eτ, причем Eτ и E’τ изоморфны тогда и только тогда, когда

Функции на С/Λ. Пусть g – мероморфная функция на С/Λ. Тогда q∙g – мероморфная функция на С, удовлетворяющая условиям q·g(z+ω1) = q·g(z+ω2) = q·g(z)
Таким образом, q∙g – двоякопериодическая мероморфная функция на С. Обратно, каждая двоякопериодическая мероморфная функция на С (так называемая эллиптическая функция) определяет некоторую мероморфную функцию на С/Λ.

Основная эллиптическая функция может быть представлена в виде ряда:

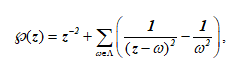
Рисунок 4 – Представление ЭК в области фундаментального параллелограмма тороидальной поверхностью

На рис. 4 изображен тор, слева развертка его поверхности (плоский лист-прямоугольник). Развертка получена двумя перпендикулярными разрезами тора: вертикальным (в сечении дает малую окружность — торцы цилиндрической поверхности) и горизонтальным вдоль образующей цилиндра, получаемого после первого разреза, и распрямления (топология) вдоль осевой линии. Линии разрезов: первая совмещается с координатной осью ординат (у), вторая — границы (верхний и нижний края развертки) равноудаленные от оси абсцисс (х). Все целочисленные точки группы ЭК в этой системе координат получают вид (х, у).

Действительно, на рисунке видим симметричное относительно оси х расположение точек. Сплошная линия на торе (синяя) без разрывов на развертке представлена 4-я отрезками, концевые точки которых соответственно имеют совпадающие координаты. Другими словами, обратными действиями (склейкой) можно получить объемную фигуру — тор, на поверхности которого все отрезки прямых воссоединятся в замкнутую пространственную винтовую линию. Условность этой иллюстрации в том, что плоская ЭК представляется в комплексной плоскости двоякопериодической функцией, удовлетворяющей уравнению Вейерштрасса.

Эта функция мероморфна на С, двоякопериодическая и имеет полюсы кратности 2 в точности в вершинах решетки Λ. Очевидно, что и производная ℘’(z) является двоякопериодической функцией, имеющей полюсы кратности 3 в вершинах решетки Λ.
℘(z) и ℘′(z) связаны между собой некоторым полиномиальным соотношением:
f(℘(z), ℘′(z), 1) = 0.

Факторизация из полезных возможностей ЭК

— разложение составного числа N на множители.
Формально алгоритм, предложенный Ленстрой содержит следующие шаги.
ш1. Выбирается ЭК над полем порядка N, т.е. целые числа из диапазона $$.
ш2. Рассматриваем кубическую кривую $$ и базисную точку ЭК $$.

ш3. Вычисляем $$; этим проверяется являются ли редукции кривой Е эллиптическими. Если НОД =N, переход к Ш1 и выбор нового b. Если $$, то получен нетривиальный делитель числа N. При $$, переход к Ш4

ш4. Выбираем число k, являющееся произведением небольших простых чисел в небольших степенях: k=НОК(2,3, …, М), где М-натуральное число.
ш5. Вычисляем кратную базисной точку $$
ш6. Вычисляем $$. Если 1 шагов, т.е. сложения точек на кривой. Более того, при вычислениях используются только значения $$.

Замечание. Обычный подход — многократное суммирование точки с собой. Ленстра заметил, что в кольце невозможность вычислить сумму точек (получить нейтральный элемент O), где необходимо вычислять коэффициент $$ возникает деление на нуль чаще чем в поле, что может приводить к нейтральному элементу O быстрее. Действительно, разность $$ обращается в нуль при значениях кратных не только самому N, но при кратных его делителям.

Пример Пусть задано составное число $$. Выберем $$ Представим $$ разложением по степеням 2. Будем вычислять
$$
$$
$$
$$ $$
Следовательно, $$.
Теперь, вычисляя $$, получаем единицу (решения нет) и переходим к ш1 для выбора нового значения k, которое увеличим в 7 раз. $$ Представим новое значение k степенями 2 $$ вычислим
$$ и редуцируем по модулю N, $$
Наконец, воспользуемся алгоритмом Евклида $$ и получаем $$, нетривиальный множитель $$

Заключение

Не любую ЭК и ее группу можно отождествлять с точками на поверхности тора, а только в случае ЭК, представляемой в комплексной плоскости.
Вольное обращение с математическими понятиями и терминами не упрощает понимание существа дела, а наоборот запутывает. Авторы публикаций часто называют порядком ЭК порядок группы ее целочисленных точек. Читатель, обратившись к учебнику или к математической энциклопедии (в 5-ти томах), останется в недоумении, прочитав статьи об этих понятиях.

О некорректности с заданием полей расширения (отсутствие неприводимого многочлена и примитивного элемента) уже упоминалось во вводной части. Как это должно работать и работает демонстрируется в AES I, где приводится в явном виде поле расширения конкретного стандарта шифрования США, AES II здесь демонстрируются примеры использования поля расширения в реализации операций шифрования/расшифрования, корректирующие коды.

Аддитивная группа поля расширения $$ раскладывается в смежные классы по подгруппе 16-го порядка. Эти классы — являются элементами факторгруппы и классами эквивалентности. Эти ссылки сделаны на реальные, работающие в действительности вещи (не абстрактные примеры), не упрощенные простенькие упражнения.

Мои ученики (не все) на этих примерах обучаются, прекрасно во всем этом разбираются и используют в своих отчетах. Это позволяет им понимать публикации в статьях об атаках на шифры, цифровые подписи, хеш функции, протоколы и др.
Ничего подобного я не вижу в статьях на Хабре, на других сайтах. Известный принцип- повторяемости результата другим исследователем авторами не поддерживается и видимо не разделяется.