Совсем недавно попалось на глаза сообщение, что группа исследователей создала очередную виртуальную модель Вселенной. Смоделировать набор данных удалось на самой быстром компьютере для астрономических исследований ATERUI II, который обладает 385 терабайт оперативной памяти. Компьютерный космос имитирует 2,1 триллиона частиц внутри куба шириной 9,63 млрд. световых лет.
В модели реализована эволюция Вселенной от Большого взрыва до наших дней. С помощью созданной программы можно узнать о ранних стадиях жизни Вселенной и смоделировать , что происходит в ее дальних уголках сейчас.
К примеру, в масштабах «Вселенной Уучу» (так назван проект, от японского «пространство») Солнечная система представляет собой дискретную микроскопическую частицу.
Но все ли так однозначно. Не внесет ли дискретность коррективы в модель Большого взрыва?
Часть 1 . Кванты
«Для нас было символом веры то, что все уравнения, описывающие фундаментальные законы Природы, должны отличаться математической красотой. Это было для нас почти религией, причем очень полезной, ибо ее можно считать основой многих наших успехов» Поль Дирак
Как известно, некоторые физические величины, относящиеся к микрообъектам, изменяются не непрерывно, а скачкообразно, принято говорить, что они квантуются.
В начале XX века немецкий физик М. Планк, изучавший тепловое излучение твердых тел, пришел к выводу, что электромагнитное излучение испускается в виде отдельных порций — квантов энергии.
Идея о квантовании энергии позволила объяснить происхождение линейчатых атомных спектров, состоящих из набора линий, объединенных в серии.

Первая квантовая теория строения атома была предложена Н. Бором. Предполагалось, что в изолированном атоме электроны двигаются по стационарным орбитам, каждой из которых отвечает дискретное значение энергии.
Дискретность энергии электрона является важнейшим принципом квантовой механики.
Электроны в атоме могут иметь лишь строго определенные значения энергии. Им разрешен переход с одного уровня энергии на другой, а промежуточные состояния запрещены.
Переход электрона из одного стационарного состояния в другое сопровождается излучением кванта электромагнитного излучения.
Так, например, согласно формуле Ридберга, длина световой волны, которую излучает атом водорода, определяется из выражения:
Очевидно, выражение для постоянной Ридберга можно переписать в виде :
Тогда для атома водорода после замены масс me и mp на комптоновские длины волн:
Рассматривая атом водорода как единое целое с характеристикой λH , можно предположить, что не только электрон, но и весь атом может находиться только в состояниях с дискретным значением энергии.
Таким образом, кратное квантование энергии на разных уровнях сложности структур материи дает возможность предположить, существование некоего фундаментального масштаба энергии E0
Введение такого масштаба позволит помочь в решении задачи квантово-метрологического эталонирования всех физических величин.
Такая задача получила высокий статус в результате революционных научных достижений рубежа XIX-XX вв. и установления парадигмы фундаментальных констант. Суть квантово-релятивистской революции можно выразить как открытие существования абсолютных эталонов, в качестве которых выступают фундаментальные константы.
В течение XX века был предложен целый ряд моделей эволюции физики, основанных на роли фундаментальных физических постоянных во взаимоотношении физических теорий.
Однако в этих моделях фундаментальным статусом наделяются десятки различных постоянных, и таким образом, их число многократно превышает количество эталонов, необходимых и достаточных для полной стандартизации физических величин.
Поэтому на основе таких постоянных был построен целый ряд различных естественных систем единиц.
Вопреки распространенному убеждению, что история естественных единиц началась с Планка и предложенной им в 1906 году системы единиц, следует отметить, что на самом деле это не так.
В качестве примера более ранних попыток их создания можно привести астрономическую систему единиц, систему единиц К.Ф. Гаусса, универсальные системы Дж.К. Максвелла.
Конечно, наибольшую известность приобрела современная версия планковской системы единиц, модифицированная в √2π раз копия оригинальной.
Однако особо хочется отметить (далее станет понятно почему) в некотором роде прародителя планковской системы — масштаб ирландского физика Дж.Стони , представленный им более чем на 30 лет раньше в 1874 году.
В современном виде единицы Стони отличаются от планковских множителем √𝛼 , где 𝛼 –постоянная тонкой структуры.
В этой системе единицы длины, времени, массы, энергии имеют следующий вид:
Отметим дополнительно, что в физике используются также электронная система единиц, атомная система Хартри, квантово-релятивистская система, квантово-электродинамическая система и другие.
Значение систем, основанных на фундаментальных постоянных c, h, e заключается в том, что они могут стать основой для конвергенции всех естественных систем единиц.
Например, в системах Хартри и квантово-релятивистской системе во всех уравнениях неявно фигурирует постоянная тонкой структуры 𝛼 , будучи включенной в определения соответственно единиц скорости и заряда. Переход к системе c, h, e приводит к тому, что 𝛼 появляется в качестве множителя в уравнениях электродинамики в явном виде. Если это и выглядит как неудобство, то компенсируется тем, что используется единственная система единиц и все физические уравнения приобретают ясный физический смысл.
Следует отметить, что система c, h, e сама по себе не фиксирует масштаба длины и энергии. Для того, чтобы система стала полной ( т.е. достаточной для эталонирования всех физических величин), должна быть открыта и /(или, если она уже открыта) приобрести фундаментальный статус еще одна размерная постоянная, не являющаяся комбинацией постоянных c, h, e .
Вернемся к предположению о существования некоего фундаментального масштаба энергии E0. Выбирая такой масштаб, с комбинацией постоянных c и h можно образовать фундаментальный масштаб длины r0 , а также фундаментальные масштабы других величин. Тогда очевидно, что произведение E0 r0 , совпадая по размерности, будет пропорционально hc.
Обозначим безразмерный коэффициент пропорциональности Nm и запишем в виде:
Теперь выразим фундаментальные масштабы длины r0, времени t0 и массы m0 через E0 :
Введем производный масштаб X пропорциональный квадрату масштаба длины, с безразмерным коэффициентом пропорциональности Nm∙Nq , причем пока Nq выбираем произвольно:
Выразим основные масштабы через масштаб X :
Можно утверждать, что полученные масштабы пропорциональны другим масштабам систем c, h, e в частности естественным единицам Стони:
Безразмерный коэффициент пропорциональности Nst назовем большим числом Стони (выбор названия станет ясен позже):
Учитывая, что коэффициент Nq выбран произвольно, закрепим его значение так, чтобы выполнялось отношение
Тогда, используя формулы (4), путем нехитрых преобразований, для постоянной тонкой структуры можно получить отношение:
а выражение для m0 записать в виде:
Как известно, в Международной системе единиц (СИ) постоянная тонкой структуры определяется следующим образом:
Тогда, приравнивая (10) и (12) получаем :
Выразим произведение hc из формулы для m0 (11) и, подставляя, получим:
Очевидно,
Q = Nq ∙ e — некоторое особое количество заряда ,
M = Nm ∙ m0 — некоторая особая «порция» массы.
Тогда (14) можно записать в виде :
Правую часть выражения можно также получить как отношение фундаментальных законов Кулона и Всемирного тяготения:
Сопоставив с (15) получаем:
Очевидно, что M и Q представляют собой некоторые универсальные величины, связанные с глобальными характеристиками Вселенной.
По аналогии из формул (15) можно сделать вывод, что величины
E = E0 ∙ Nm , R = r0 ∙ Nm и T = t0 ∙ Nm также принадлежат к этой категории.
Упорядочим выражения для фундаментальных масштабов и универсальных характеристик Вселенной и запишем их как блок (18):
Безразмерные величины Nm и Nq можно назвать глобальными количественными параметрами Вселенной. Они связывают между собой параметры микро- и макромира .
Выделим некоторые соотношения:
Отдельное внимание обратим на выражение для постоянной тонкой структуры 𝛼 .
Как известно, постоянная тонкой структуры (ПТС) 𝛼 — это фундаментальная константа, которая характеризует силу электромагнитного взаимодействия.
Константа имеет колоссальное значение для теоретической физики и космологии, поскольку она определяет характер наиболее общих законов, которые лежат в основе эволюции космоса.
Свое название величина 𝛼 получила в связи с работой Арнольда Зоммерфельда [1] о тонкой структуре линий водорода, которую он выполнил при исследовании спектральных серий в рамках теории Бора.
Авторы «Берклеевского курса физики» ( курс физики, созданный преподавателями Калифорнийского университета в г. Беркли, США ) считали, что точнее называть ее постоянной основной структуры [2, с.81] и отмечали следующее : «Постоянная тонкой структуры является одной из истинно фундаментальных констант природы. В настоящее время это чисто эмпирическая константа, так как у нас нет теоретического объяснения ее величины. Если бы она имела большее значение, мир выглядел бы совсем по-другому, можно сказать невыразимо иначе»[2, с.63].
Один из создателей квантовой механики, немецкий математик и физик-теоретик, лауреат Нобелевской премии по физике Макс Борн высказывался о ПТС следующим образом:
«Более совершенная теория должна была бы вывести число 𝛼 с помощью чисто математических рассуждений, не ссылаясь на результаты измерений … Ясно, что объяснение числа 𝛼 есть одна из центральных проблем естествознания» [3, с. 704, с.711].
Известный американский ученый Ричард Фейнман также считал раскрытие сути ПТС одной из важнейших задач современной физики:
«С тех пор, как его открыли свыше пятидесяти лет назад, это число остаётся тайной. Все хорошие физики-теоретики выписывают это число на стене и мучаются из-за него. … хотелось бы узнать, как появляется это число: выражается ли оно через π, или, может быть, через основание натуральных логарифмов? Никто не знает. Это одна из величайших проклятых тайн физики: магическое число, которое дано нам и которого человек совсем не понимает. Можно было бы сказать, что это число написала «рука Бога», и «мы не знаем, что двигало Его карандашом». Мы знаем, что надо делать, чтобы экспериментально измерить это число с очень большой точностью, но мы не знаем, что делать, чтобы получить это число на компьютере – не вводя его туда тайно!» [4]
Из блока формул (18) видно, что ПТС является некоторым отношением глобальных количественных параметров Вселенной Nm и Nq .
Провести численную оценку этих параметров можно отталкиваясь от разных предположений, выбирая в качестве универсальных характеристик M, R, T какие-либо значимые физические величины.
Но наиболее интересные результаты можно получить, ассоциируя эти величины с глобальными характеристиками Вселенной, и отталкиваясь от предположительных значений этих характеристик, рассчитанных согласно существующим космологическим моделям.
Такое решение в условиях нестационарности Вселенной впоследствии приведет нас к определенным осложнениям и очень оригинальным, но фальсифицируемым выводам, которые будут рассмотрены во второй части.
Итак, по современным представлениям https://en.wikipedia.org/wiki/Observable_universe Вселенная представляет собой шар со следующими радиусом и массой:
Исходя из верности этих данных получаем для Nm два варианта :
Далее, согласно модели ΛCDM, возраст Вселенной составляет 13.799 +/- 0.021 млрд. лет и следовательно :
Таким образом, получаем следующую оценку :
Отметим корреляцию значения Nm c энергетическим «большим числом» Дирака NDW [5], которое вычисляется как отношение энергии Вселенной к «нулевой энергии»:
где Н0 — постоянная Хаббла.
«Большие числа» Дирака относятся к исследованиям Полем Дираком отношений размеров Вселенной к размерам элементарных частиц, а также взаимосвязи сил различных масштабов.
В частности, отмечалось, что отношение радиуса наблюдаемой Вселенной к классическому радиусу электрона, возраста Вселенной к атомному времени, обратная величина гравитационной константы связи приблизительно равны и численно оценивались как 1040. Теперь из (19) эти отношения можно дополнить более масштабными:
Можно также оценить Nm , исходя из значения критической плотности Вселенной :
Критическая плотность Вселенной — выделенное значение плотности материи (вещества и энергии) Вселенной, от которого зависят глобальные геометрические свойства вселенной в космологических моделях.
В частности, если средняя плотность Вселенной меньше (пространство с отрицательной кривизной, открытая вселенная) или равна (плоская, открытая вселенная) критической, то реализуется бесконечная вселенная. Если же плотность больше критической (положительная кривизна пространства, вселенная замкнута) — то пространство Вселенной оказывается конечным:
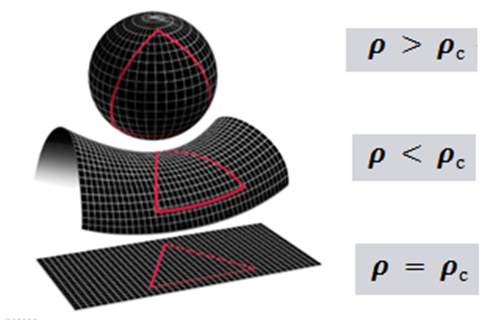
По данным WMAP (Wilkinson Microwave Anisotropy Probe — космический аппарат НАСА, предназначенный для изучения реликтового излучения) для наблюдаемой Вселенной и согласно модели Фридмана, средняя плотность Вселенной равна критической с точностью порядка 1%.
Тогда, учитывая современные вариации значений постоянной Хаббла, плотность вселенной оценивается как 9 * 10-27 kg/m3 и, принимая значение H0 в соответствии с последними данными Planck 2018 results. VI. Cosmological parameters [6], получаем следующую оценку для Nm :
Значение Nq легко оценить из (10) поскольку значение ПТС известно с огромной точностью.
По данным CODATA 2018 𝛼 = 0.0072973525693(11) . Выбирая предположительно входящее в корректный диапазон значение Nm из (20) , для Nq получаем:
Теперь, подставляя в блок (18) значения Nm и Nq , оценим порядок значений фундаментальных масштабов (квантов) и особого количества заряда Q :
Предположения о существовании фундаментальных масштабов и попытки количественно оценить их ранее предпринимались неоднократно.
Например, в работе известного профессора астрофизики и теоретической физики Пола С. Вессона «IS MASS QUANTIZED?» [7] вычисленное значение элементарной массы приблизительно равно
В статье физика из Европейской организации по ядерным исследованиям (ЦЕРН) Драгана Гайдуковича «On the relation between mass of a pion, fundamental physical constants and cosmological parameters» [8] для фундаментальной массы представлено следующее значение
Также интересен интервал, указанный в работе бразильских ученых из INPE-Instituto Nacional de Pesquisas Espaciais «Can Massive Gravitons be an Alternative to Dark Energy?” [9]
Аргентинский физик-теоретик Марсело Сэмюэль Берман в статье «ARE MASS AND LENGTH QUANTIZED?» [10] приводит следующие порядки для фундаментальных масштабов:
Что касается физического смысла, который несет количество заряда Q — это отдельный вопрос.
В современных физических моделях заряд разделяется на положительный и отрицательный, с XVIII века общепризнанным считается закон сохранения электрического заряда.
Еще в 1733 г. французский химик Ш.Ф. Дюфе обнаружил, что наэлектризованные разные тела могут не только притягиваться, но и отталкиваться и выдвинул гипотезу о существовании разного типа электричества «стеклянного» и «канифольного». Но Б.Франклин экспериментально показал, что «стеклянный» заряд нейтрализует «канифольный» и предположил, что существует заряд только одного типа.
Таким образом, понятие «заряд» у Франклина — единственно, можно лишь обнаруживать его избыток или недостаток в каком-то теле. Позже наука окончательно разделила заряд на два знака, а насколько такая дифференциация легальна, тема в физике сейчас не самая актуальная.
В отношении Q чисто гипотетически можно задать вопрос: есть ли вариант, что это предельная величина заряда сферы или шара радиуса R ?
Литература
[1] A. Sommerfeld, Atombau und Spectrallinien, I Band, Friedr. Vieweg & Sohn, Braunschweig, 1951. [2] Э. Вихман «Квантовая физика» Берклеевский курс физики. Т.4 [3] Макс Борн Таинственное число 137. УФН, 1936 г., Т. XVI, вып. 6. [4] Ричард Фейнман Лекция 4. Нерешенные вопросы «КЭД – странная теория света и вещества» [5] J. Casado (2004). Connecting Quantum and Cosmic Scales by a Decreasing-Light-Speed Model [6]. Planck 2018 results. VI. Cosmological parameters Planck Collaboration [англ.] // Astronomy and Astrophysics. [7] “IS MASS QUANTIZED?” Paul S. Wesson Dept. of Physics, University of Waterloo, Waterloo, Ontario N2L 3G1 Canadahttps://cds.cern.ch/record/644227/files/0309100.pdf
[8] «On the relation between mass of a pion, fundamental physical constants and cosmological parameters» Dragan Slavkov Hajdukovic PH Division CERN CH-1211 Genevahttps://arxiv.org/ftp/arxiv/papers/0810/0810.4678.pdf
[9] “Can Massive Gravitons be an Alternative to Dark Energy?” M. E. S. Alves, O. D. Miranda and J. C. N. de Araujo INPE-Instituto Nacional de Pesquisas Espaciais — Divis˜ao de Astrofısica, Av.dos Astronautas 1758, S˜ao Jos´e dos Campos, 12227-010 SP, Brazil, 2009https://arxiv.org/pdf/0907.5190v1.pdf
[10] “ARE MASS AND LENGTH QUANTIZED?” 2007 Marcelo Samuel BermanInstituto Albert Einstein — Av. Candido Hartmann, 575 — # 17 and 80730-440 — Curitiba — PR – Brazil


