Газодинамика сверхзвукового сопла Лаваля.
Газодинамика сверхзвукового сопла Лаваля.
Когда-то много лет назад я пытался разобраться в физических принципах работы жидкостного реактивного прямоточного двигателя ( далее ЖРД), но упёрся в глухую стену из математических выкладок без качественных физичных объяснений самих процессов.
Пришлось выдумать собственный взгляд на атомную физику в целом, чтобы в итоге подойти к пониманию таких казалось бы изученных вопросов, как «Подъёмная сила крыла» и «Газодинамика работы ЖРД».
Теме «Подъёмная сила крыла» посвящены предыдущие семь глав соседней длинной многолетней статьи ( https://habr.com/ru/post/438854/ ), а теперь настала пора соединить её воедино с темой «Модель твёрдого Ядра без электронных оболочек, то есть Ядро равно всему атому по размеру» ( https://habr.com/ru/post/440848/ ).
Именно написание статьи про устройство атома подтолкнуло меня в изучение аэродинамики, чтобы там найти феномены, объяснимые только моей теорией Статического отталкивания в газах (далее СТГ) , что позже привело и к моему пониманию физики работы ЖРД.
Физическое описание работы ЖРД.
Дальнейший разбор принципов работы ЖРД буду вести на основании фактических данных и теоретическо-эмпирических формул из общедоступного современного учебника по «Теории ЖРД» (1), где изложены факты и актуальные теоретическо-эмпирические формулы описывающие поведение реальных ЖРД.
То есть я не собираюсь опровергать огромный массив знания, накопленного за последние 80 лет изучения реальных ЖРД, но попытаюсь дать новую трактовку известных данных через призму новой физической модели существования газов.
Обход противоречий Кинетической теории газов.
Основные проблемы термо- газодинамики и термодинамические противоречия в работе ЖРД снимаются, если отказаться от Кинетической теории газов (далее КТГ) и принять Статическую теорию газов (СТГ), функционирующую на полях взаимного статического отталкивания между молекул газа.
По СТГ молекулы газов висят неподвижно, а их тепловая энергия заключена в сжатом упругом поле отталкивания вокруг них.
Так по СТГ получается упругая среда с малоподвижными массами молекул газа в узлах полей отталкивания.
По факту же между массами молекул действуют центральные силы отталкивания, которые можно уподобить пружинам, подчиняющимися при сжатии-растяжении некоторым фиксированным законам, которые при пересчёте на объёмные показатели совпадают с известными термодинамическими формулами.
То есть газы вовсе не состоят из бешено носящихся со скоростями ружейной пули молекул, при этом постоянно соударяющихся друг с другом.
Надо ещё особо отметить, что в КТГ на микроуровне не выполняется закон сохранения импульса.
Так в КТГ при столкновении молекул разных масс невозможен перевод части кинетической энергии в тепло при упругом их соударении с сохранением суммарного импульса после столкновения. Ведь тепло — это и есть кинетическая энергия молекул согласно КТГ.
Так же по КТГ должна быть почти мгновенная передача тепла через газовые слои (с тепловой скоростью молекул).
В реальности газовые прослойки при отсутствии конвекции имеют очень высокое сопротивление теплопередаче , то есть при теплопередаче без конвективного теплопереноса через газовые слои сверху вниз тепло передается крайне медленно (почти как в вакууме).
Из сказанного получается, что исходные допущения КТГ противоречат базовым законам физики-механики в самой своей основе!
В то же время по модели СТГ молекулы газа окружены полями взаимного отталкивания, с помощью которых они вполне статично висят в пустом объёме, слабо колеблясь при передаче звука (см.рис.1) и почти не перенося тепло в адиабатических звуковых колебаниях.
При этом в СТГ даже закон сохранения импульса при столкновении разномассовых молекул может выполнятся, так как кинетическая энергия от скорости полёта молекулы не связана с внутренней (тепловой) энергией молекулы газа. Кинетическая энергия молекулы по СТГ может переходить в тепло, выраженное давлением поля (напряжением центральных сил) отталкивания.
То есть по СТГ возможны варианты разных комбинаций кинетической и тепловой энергии в молекулах газа:
-
летящие в пустоте быстрые и холодных молекулы c сильно растянутым в пустом пространстве слабо напряженным полем отталкивания (именно такие молекулы должны вылетать из идеального ЖРД в вакууме). Замечу, что по СТГ у летящей сквозь космос молекулы газа появляется объективная температура, независимая от системы отсчёта определения её скорости и соответствующей этой скорости кинетической энергии.
-
медленные горячие молекулы, висящие неподвижно в сосуде под давлением газа; -группы горячих молекул, коллективно летящих на высокой скорости внутри сосуда под давлением (спутник в космосе). Подробнее об этом в моей статье «Модель твёрдого Ядра без электронных оболочек, то есть Ядро равно всему атому по размеру» на ХАБР по ссылке: https://habr.com/ru/post/440848/ и краткая версия с дополнениями о фазовых переходах на Дзен https://zen.yandex.ru/media/id/5db6a0ee95aa9f00b106a116/fazovye-perehody-v-vescestve-s-tochki-zreniia-fiziki-atomnogo-iadra-5dc3010ee882c300aef791c7

Рис.1 Схематическое изображение пограничной зоны контакта разных фаз Жидкость-Газ (Вода-Воздух) в случае Статической Теории существования Газа:
а) Газ при давлении 1 атм ( плотность воздуха 1,2кг/м3) над жидкой водой (расстояние между центрами молекул приблизительно в 10 раз больше, чем в жидкой фазе);
б) Тот же газ над водой при той же температуре, но при давлении 10 атм (плотность 12кг/м3)., при этом расстояние между центрами молекул газа сокращается в 10^0,333=2,15 раз. Такие же расстояния между молекул газа в КС ЖРД, но уже при давлении 100 атм и температуре 3800К.
Отчётливо видно деформацию соприкасающихся монополярных электрических корон атомов газа при сближении молекул. Силовые линии не могут пересекаться, а потому вынуждены деформироваться, занимая меньший объём, что и приводит к росту центральных сил взаимного отталкивания (рост давления газа).
Внедрение СТГ в привычное описание работы ЖРД
Течение потока реактивной струи в реактивном двигателе подчиняется закону сохранения вещества, а потому в стационарном режиме работы двигателя с постоянным расходом топлива и постоянной тягой в любом поперечном сечении двигателя проходит постоянное одинаковое количество вещества.
Так как в каждом параллельном поперечном сечении двигателя разные скорости потока, разные площади сечения, разные давления и плотности протекающих газов, то постоянный массовый расход G можно определить через физические параметры газа и геометрию сопла.
Так в интервал времени дt через сечение площадью S протекает газ со скоростью V и плотностью q.
Тогда расход массы за время дt составит:
дG=дt*V*Sq
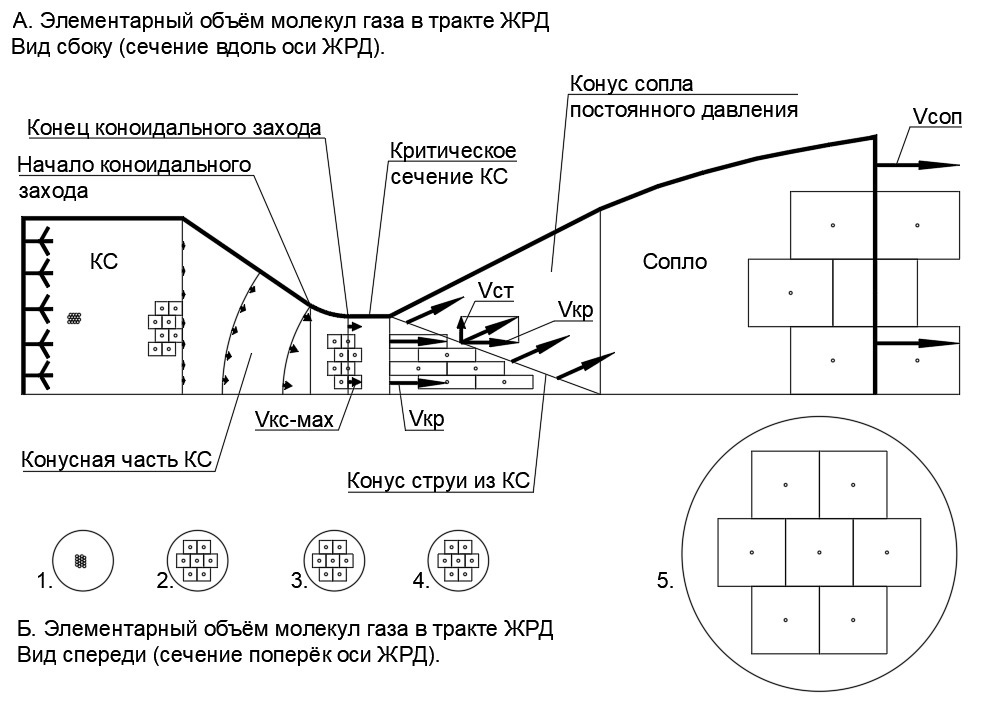
В этом выражении произведение дtVS= дW, где дW — это объём элементарных параллельных дисков пространства сопла, в которых содержится постоянное одинаковое количество вещества (см.рис.2).
Толщина этих дисков зависит только от скорости потока V в данном сечении сопла. Толщина диска дН=дtV
Площад S этого диска зависит только от геометрии сопла в данном сечении.
Плотнось q зависит только от величины дW при постоянном расходе G (кг/с), где
дG =дt* G
А плотность равна
q=дG/дW
откуд.
дW= дG/ q
Для рассмотрения физики газодинамических процессов в реактивном сопле важна именно плотность среды, как отношение объёма пространства, приходящееся на одну молекулу вещества газа.
В границах теории СТГ вообще становится возможным рассматривать одну молекулу газа, висящую в окружении своего поля отталкивания в своём элементарном объёме.
На сводном Графике параметров газа по длине сопла имеется параметр плотности, по которому можно определять объём дW элементарного слоя в каждом сечении (см.рис.2).
Откуда через диаметр , как и вполне доступный геометрический размер в сечении, можно легко рассчитать параметр S данного элементарного слоя в этом сечении. Правда данный график не имеет чёткой размерности, а потому не может служить источником точной цифровой информации.
Существует более точный график из более специализированного учебника по «Теории ЖРД» [1], где графики представлены значительно точнее, а размерные оси оцифрованы (см.рис.3).
Правда в более точном графике (рис.3) отсутствует параметр плотности. Это косвенно демонстрирует наличие неувязок в термодинамических формулах ЖРД, которые при наличии графика плотности стали бы вопиющими.
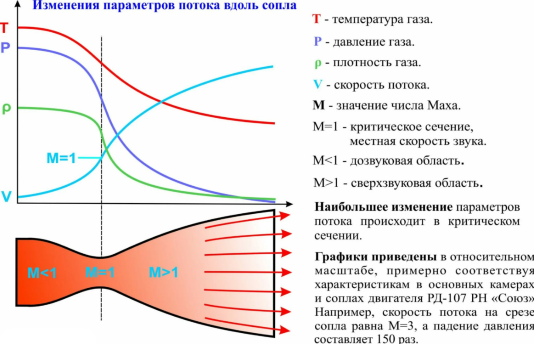
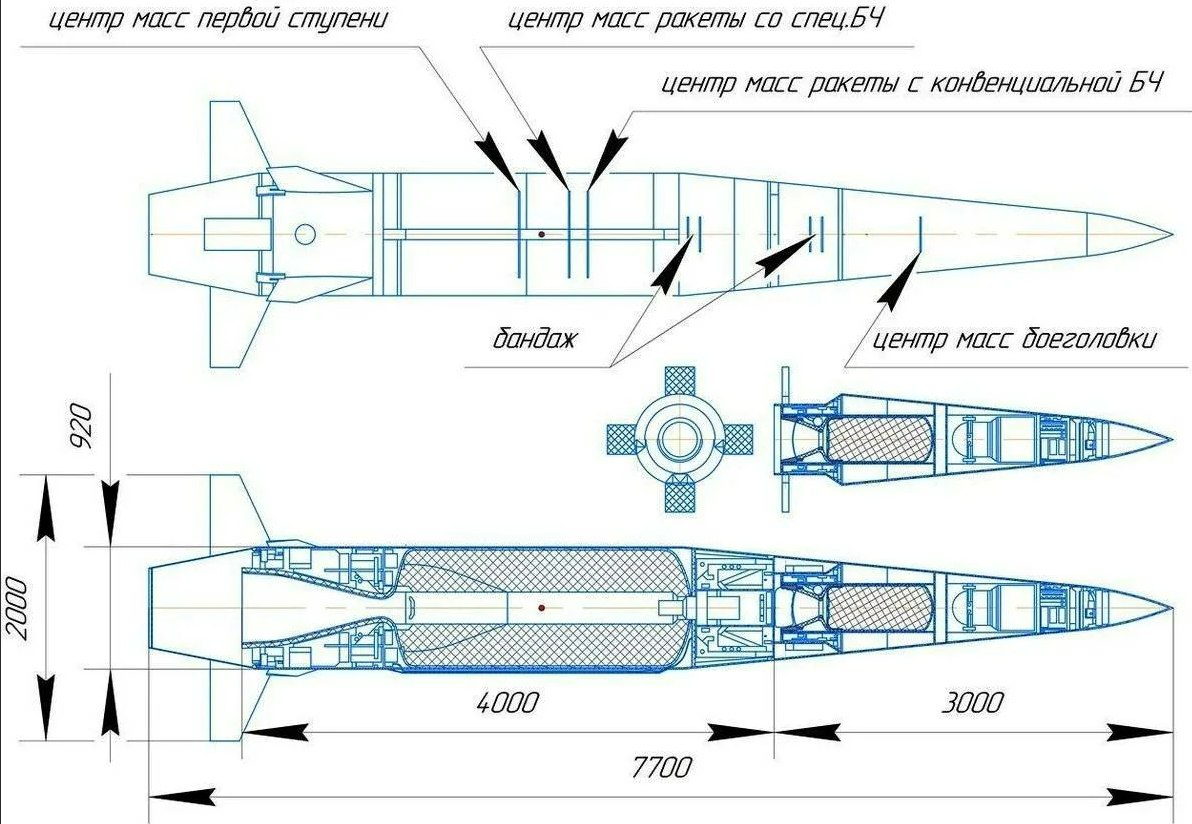
Рис.2. Классическая обобщённая картинка с графиком из учебника для объяснения принципов работы и газовых состояний рабочей среды в ЖРД, дающая качественное описание с мелкими огрехами по точности, но с дополнительным графиком плотности газа по длине ЖРД.

Рис.3. Достаточно точный комбинированнный график из учебника для объяснения принципов работы и газовых состояний рабочей среды в конкретном ЖРД, где лучше демонстрируется происходящее в КС и на кромке сопла ( локальное изменение масштаба шкалы Р).
Из величин S и дW можно однозначно получить осевую скорость V в любом сечении ЖРД:
V= дW/(S*дt)= (дG/ q)/(S*дt)= дG/ (q*S*дt)= G/ (q*S)
В итоге мы получили выражение для скорости в сечении с однозначной зависимостью от параметра плотности (q), параметров определяемых геометрией самого сопла в данном сечении (S) и режимом работы двигателя в целом (G).
Так получается, что элементарный газовый объём (содержащий одну и туже порцию вещества) в работающем РД имеет непостоянный объём и непостоянную форму при перемещении по оси РД. (см.рис.4)
Непостоянство формы элементарного газового объёма по длине ЖРД (см.рис.4) предполагает изменение соотношения R/дН. Это соотношени R/дН определяет количество единичных молекулярных столбцов в диаметральном сечении к количеству единичных молекулярных дисковых слоёв в объёме дW при равномерном распределении молекул в объёме.
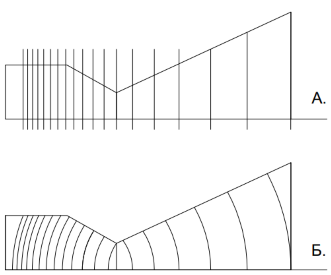
Рис.4. Распределение толщины слоя дW =дt*V одной доли вещества по осевому ходу в прямоточном РД:
А. Плоские параллельные слои с толщиной, пропорциональной скорости на оси (понятное соотнесение с графиком V на рис.1).
Б. Сферические слои с толщиной, пропорциональной скорости на оси. Выпуклости слоёв направлены в сторону доминирующего из действующих на арку усилий сжатия (избыточное давление в КС и ускорение разгона молекул газа в сопле Ловаля).
Если считать, что внутри элементарного объёма dW послойное расположение молекул газа не меняется, то геометрическое изменение сечения сопла будет вызывать такое же изменение расстояния между молекулами в единичном слое, при этом расстояние между слоями будет связано с осевой скоростью потока.
Такая структурная неоднородность в газе может возникнуть при быстро текущих адиабатных процессах, когда равномерное распределение молекул не успевает восстанавливаться из-за преобладания однонаправленного изменения объёма с высокой скоростью.
Подобный скоротечный адиабатный режим осуществим и при разгоне газа до околозвуковой скорости, что и наблюдается вблизи критического сечения в КС ЖРД.
Именно этот вопрос о рекомбинации молекул в единичном объёме dW по длине КС и сопла ЖРД в зависимости от скорости потока будет предметом подробного рассмотрения в данной статье.
В дальнейшем рассмотрении поведения газов в ЖРД будет исходить из положений СТГ, которые позволяют рассматривать свойства газа в большом объёме на примере поведения одиночной молекулы газа в её персональном молекулярном объёме, в котором молекула висит за счёт окружающих её сил отталкивания ближнего порядка от ближайшего ряда молекул в окружении.
Рассмотрение поведения отдельной молекулы газа в её персональном объёме по СТГ
Рассмотрение поведения отдельной молекулы газа в её персональном объёме по СТГ.
Изменение скорости – это ускорение.
Ускорение — это следствие действия силы на молекулу газа с некой массой (разница противоположно направленных сил = равнодействующая сила).
Для разреженных газов роль такой направленной силы является разница давлений между единичными слоями газа.
Таким образом мы ввели неравновесную плотность газа между соседними рядами молекул в привязке к направлению изменения скорости перемещаемого объёма :
-вдоль оси ЖРД будет плотность qv,
-
поперёк ЖРД будет плотность qs. Также мы выявили разницу давлений на границе слоя, инициирующую ускорение движения данного слоя по оси РД Возникает вопрос: А имеем ли мы право так вольно обращаться со свободно перемещающимися молекулами газа, заставляя их сохранять послойное состояние? Ответом служит известны феномен Звуковой волны, где звук распространяется в параллельных слоях, меняя послойные расстояния вдоль направления распространения звука, при этом не меняя расстояния между молекулами вдоль фронта волны по слоям (перпендикулярно к направлению распространения звука). По КТГ мы разделяем по ортогональным направлениям кинетическо-тепловую энергию молекул газа, выделяя только 1/3 на направление перемещения звуковой волны. Именно эта 1/3 тепловой энергии в одном направлении определят ограничение скорости звука. То есть кинетическая энергия на скорости звука должна быть равна 1/3 общей тепловой энергии молекулы газа выраженой в кинетической энергии по одному направлению. Из этого по законам механики следует равенство .
Vа^2*Mr/2=(1/3)*Emr= R*T
Откуда: Vа^2=2*R*T/Mr
Vа=(2*R*T/Mr)^0,5
В классической «кинетической теории газов» вместо множителя 2 в правой части присутствует показатель адиабаты 1,4 ( для двухатомного газа и воздуха 7/5=1,4). То есть наше предположение отличается от существующей теории на величину Ктеор=(2/1,4)^0,5=1,195 Разница в скорости составит 1,2 раза или на 20%. Причём наша расчетная скорость выше «классической» расчётной скорости звука. Тут сразу есть некоторые дополнения. Обычно на бытовом уровне в качестве скорости звука воспринимают скорость движения фронта волны, что и определяется обычно в экспериментах при измерении скорости звука по отставанию звука выстрела от вспышки выстрела. Но в случае передачи плоской волны в упругой среде максимальная скорость отдельной молекулы будет отличаться от средней скорости фронта волны.
При идеально упругом колебательном движении это отличие составляет Vмах=1,41*Vср
Где 1,41= 2^0,5.
В качестве примера можно предложить взглянуть на переменный электрический ток в металлических проводах, который также является плоской волной «электронного газа» в условной «трубе» провода. Так именно на такую величину 1,41 отличается действующее напряжение U= 220В в электрической сети переменного тока от максимальной амплитуды напряжения Uмах=310В в синусоиде (см.рис.5): Uмах =220*1,41= 310 В
Мало кто слышал о напряжении Uмах =310 В, но если задать правильный вопрос интернету, то в ответ сразу вываливаются графики синусоиды действующего напряжения U=220В (среднее за полупериод) с максимумом горба волны на Uмах=310 В.
У обывателя на слуху больше величина U=380 В трёхфазного напряжения (см.рис.6), где:
U=380= 220*(3^0,5)= 220*1,73
При этом есть ещё интересные цифры в электротехнической среде :
230*1,73=400В
Цифра 230В и 400В (или 0,4кВ) также часто встречается в технической среде электротехников (см.рис.7).

Рис.5 Синусойда действующего напряжения электрической сети 220В с максимумом на 310В.

Рис.6 Векторное взаимодействие фаз трёхфазного электроснабжения 3х380В.

Рис.7 Распределение напряжения по сети электроснабжения 220В по длине сети с учётом потерь в проводах.
В нашем случае отличие 1,2 раза не попадает ни в классическую теорию с коэффициентом адиабаты 1,4 (для воздуха), ни в нашу теорию об одностороннем расширении газов в звуковой волне.
Экспериментальные данные в нормальных земных условиях дают скорость звука 331м/с.
Откуда максимальная скорость по направлению будет:
Vа-max=331*1,41=468м/с.
И эта оценка для Vа-max= 468м/с даёт практически точное попадание в полную тепловую энергию газа в результате расчёта по привычной формуле
Vт=(3*R*T/Mr)^0,5=484м/с
с погрешностью всего в 3,5% для молекулярного веса воздуха Mr=0,029кг/моль:
484/468=1,035 или 3,5% разницы
В ниже приведённой картинке из Википедии (см.рис.8) тепловая скорость молекул воздуха заявлена Vт=464м/с при +20С, что вообще точно совпадает с полученной нами скоростью Vа-max= 468м/с!
Хотя в статье из Википедии не уточняется по какой именно из формул эта скорость получена и с какой принятой молярной массой газов воздуха (воздух- это смесь газов).
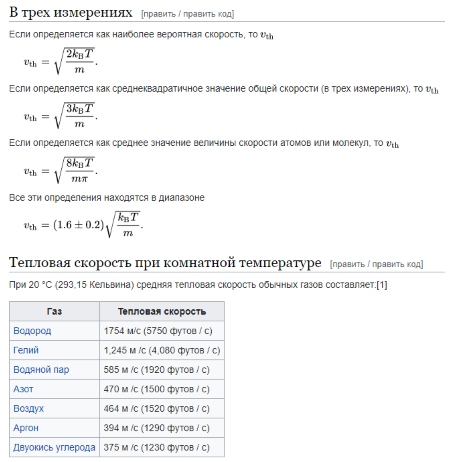
Рис.8. Страница из Википедии с набором формул по КТГ для различных тепловых скоростей молекул и таблица с непосредственно цифрами этих скоростей для разных газов.
Скорость фронта звуковой волны- это один из немногих достоверных параметров работы воздуха (газа), который измеряется напрямую достаточно простыми средствами с высокой точностью.
Так что в величине скорости звука в воздухе сомневаться не приходится.
А вот о тепловых скоростях молекул можно только гадать на основании разных теоретических предположений.
Из приведённых расчётов получается , что при звуковых колебаниях на одно направление полностью срабатывается вся тепловая энергия (кинетическая энергия), а не только статистическая доля в 33% по этому направлению.
Получается, что по КТГ отдельные молекулы газа должны организованно устремится по направлению распространения фронта звуковой волны, забыв о всех остальных направлениях движения. При этом по КТГ вдоль фронта волны в тонком слое молекул отсутствует взаимодействие (давление), так как весь фронт всю свою кинетическую среднеквадратичную энергию выстрелил в направлении распространения звука.
Вот только такого обнуление давления во фронте звуковой волны не наблюдается на практике, так как давление воздуха никогда не падает до нуля (полный вакуум) в поперечном направлении к фронту звуковой волны.
Получается, что энергия поперек скорости звука в слое вообще не расходовалась и давление в слое в направлении вдоль слоя не изменилось!
Но тогда общая полная энергия одной молекулы газа должна быть в разы выше, чем считалось ранее по КТГ.
По аналогии можно предположит похожий сценарий поведения газов в ракетном двигателе, где тепловая энергия неподвижного газа (выраженная давлением и температурой) срабатывается в кинетическую энергию высокоскоростного потока этого же газа при премещении по оси РД.
Так если вся тепловая энергия срабатывается по одному осевому направлению с достижением расчётной «звуковой» скорости, то дальнейшее наращивание скорости уже невозможно из-за отсутствия свободной энергии.
Но тогда за счёт какой энергии происходит разгон в сопле Лаваля до сверхзвуковой скорости после преодоления критического сечения ЖРД?
Получается, что тепловая энергия газа может быть разделена по направлениям, и в поперечном направлении слоя газа в критическом сечении КС тепловая энергия ещё не была израсходована.
И это предположение подтверждается энергетическим расчётом для газов в КС ЖРД!
Необходимо найти «пропавшую» часть энергии газа, которая покидает КС в огромном количестве (более 70% общей кинетической энергии струи из ЖРД) и срабатывается в сопле Лаваля на почти 2-х кратное ускорение газов.
Сравнение топливного энергетического баланса ЖРД с теоретическим газодинамическим балансом по КТГ.
Сравнение топливного энергетического баланса ЖРД с теоретическим газодинамическим балансом по КТГ.
Расчёт по химической энергии топлива.
Расчёт№ 1
Зайдём к вопросу энергобаланса ЖРД с тепло-механической стороны.
Мы знаем, что в ЖРД сжигают 1 кг керосина с теплотой сгорания 42МДж /кг и температурой газов 3800К, при этом расходуется 2,7 кг кислорода.
В результате получается струя газов с общей массой m=1+2,7=3,7кг и со скоростью истечения 3400м/с при температуре 1800К (см. граф .рис.3.).
Посчитаем баланс теплотворной энергии топлива и кинетической энергии у струи газов из ЖРД.
Ек= V^2*m/2=3400^2*3,7/2= 21 386 000Дж= 21,38 МДж
То есть баланс сошёлся практически идеально, учитывая остаточную энергию температуры струи 1800К от исходной 3800К в КС (см.рис.1-б), что даёт остаток энергии в струe по температуре 1800/3800=0,473 или 47,3%.
При этом кинетическая энергия составляет 52,7% от тепла сгорания топлива, что совпадает с тепловым КПД (2000/3800)=52,67%.
Етоп=21,38/0,527= 40,57МДж
Разница между 42 и 40,57 МДж составляет всего около 3,5%, что частично списывается на нагрев и испарение топлива (керосин) и окислителя (жидкий кислород). Также присутствует погрешность замера температур и скоростей (как на ЖРД так и на графике рис.3.), что не позволяет получить 100% точность расчётов.
Реакция горения проходит в газообразной фазе обоих компонентов при постепенном испарении керосина и кислорода с поверхности микрокапель распылённых в объёме КС жидких компонентов топлива, при этом энергия на испарение вычитается из энергетического выхлопа реакции окисления.
Перевод жидкостей в газообразное состояние внутри КС имеют весьма конкретную и существенную величину (теплота фазового перехода).
Теплота испарения керосина Q=280кДж/моль=0,28МДж/кг
Теплота испарения кислорода Q=3,41кДж/моль
Испарение 2,7кг кислорода О2 с молярной массой 0,032кг/моль потребует затрат энергии
Еисп-о=3,412,7/0,032=287,7кДж=0,288МДж
Что составит
Еисп-топ/Етоп=(0,288+0,28)/42=0,0135 или 1,35% энергии сгоревшего керосина.
Данным расчётом теплоты испарения мы нашли 1,35% энергии сгоревшего топлива из посчитанной величины 3,5% невязки в балансе по расчёту. Оставшиеся 2 % уходят на тепловые потери сквозь стенки ЖРД и на работу турбонасосного агрегата, нагнетающего топливо в КС под высоким давлением.
То есть при анализе режимов работы ЖРД вполне допустимо использовать привычные формулы механики по Ньютону.
Если считать сопло бесконечным, а конечную температуру газа равной нулю, то предельная скорость газа должна составить:
Vмах=(Ет2/Мтоп)^0,5=(40 570 0002/3,7)^0,5=4682м/с
Эта цифра нам ещё пригодится.
Проверка тепло-механического энергобаланса по КТГ
Пересчитаем тепловую энергию топлива на один моль газа в смеси СО2+Н2О в пропорции 1:1 по объёму (числу молей).
Из чего можно рассчитать среднюю молярную массу смеси газов ( СО2+Н2О):
((12+162)+(12+16)) /2= (44+18)/2=62/2=31 г/моль=0,031кг/моль
Кинетическая энергия струи из ЖРД составит
Ек-mr=21,380,031/3,7=0,179МДж/моль
Теперь проведём тот же расчёт для начального состояния и конечного состояния газов по уравнению полной энергии для 1 моль газа:
Eтmr=3*R*T
Необходимо также проверить баланс по кинетической энергии струи.
На срезе сопла поток имеет кинетическую энергию от скорости Vсоп=3400м/с и тепловую энергию от температуры 1800К, которые в сумме должны давать энергию сгорания топлива в КС:
Eжрд=Екин+Етmr
Ежрд=Vсоп^2*Mr/2+3*R*Tсоп =3*R*Tкс
Откуда нам надо получить равенство энергий:
Vкс^2*Mr/2 =3*R*(Tкс-Тсоп)
Посчитаем отдельно левую и правую части по имеющимся данным:
Vкс^2*Mr/2=3400^2*0,031/2=179 180 Дж
3*R*(Tкс-Тсоп)=3*8,3114*(3800-1800)=49 868 Дж
Мы получили отличие энергий в 179180/49868=3,59 раза, что крайне далеко от совпадения с теорией.
Тогда реальный расчётный баланс ЖРД будет выглядить так:
Vкс^2*Mr/2 =(3*3,59)*R*(Tкс-Ткр)
То есть теперь как-то надо объяснить появление нового коэффициента Кр=3,59*3=10,77 в газовой термодинамике ЖРД. Вполне возможно, что для данного ЖРД больше подходит показатель адиабаты к=1,1 Вывод по расчёту энергобаланса ЖРД: Из приведённого расчёта видно, что учебник даёт вполне точное согласование тепло-механического баланса кинетической и тепловой энергий на срезе сопла Лаваля с теплотворной способностью топлива в КС, но с подгоном показателя адиабаты к показателю Кр(к) по топливному энергобалансу. Правда при к=1,1 и адиабатическом расширении от 100атм при 3800К до 1 атм на сопле Лавля температура оказывается не опускается до необходимой нам Тсоп=2200К, а оказывается на уровне 2500К, что сильно выше необходимого по термоблансу. Стоит заметить, что для обычного воздуха с показателем адиабаты к=1,4 подгонный коэффициент энергосодержания Кр=1,4/(1,4-1)=3,5. То есть даже для обычного воздуха разрыв теории ЖРД с другой обычной теорией из учебника КТГ составляет 3,5/3= 1,166 раза или 17%, что довольно много для игнорирования. Но это уже мои «придирки» к редактору учебника…))) Рис.9. Расчётные формулы из учебника. Рис.10. Расчётные формулы из учебника. Рис.11. Расчётные формулы из учебника. Доли импульса тяги ЖРД приходящиеся на критическое сечение КС и на сопло Лаваля. То есть тяга РД на границе критического сечения без закритической части превышает в 1,234 раза тягу Fкс: Fкр=1,234Fкс При этом Fкc рассчитана по формуле: Fкс=SкрРкс. Где Fкс- тяга от статического давления дна КС на площади критического сечения, Sкр- площадь критического сечения КС, Ркс- давление в КС на дне (равно давлению наддува и впрыска камеры). Рис.12. Фрагмен текста учебника с таблицей, где написано (выделено жирном в третьей строчке таблицы 3.1), что тяга РД на границе критического сечения без закритической части превышает в 1,234 раза тягу КС Fкс=Sкр*Ркс. Бытовая логика заставляет нас считать, что скоростной напор струи из сосуда под давлением должен быть равен давлению в сосуде. И это действительно так для несжимаемой жидкостей! Fтяги=2*Fр Парадокс о превышении тяги от струи из отверстия над нескомпенсированным давлением жидкости на площади отверстия. При этом на площади проекции отверстия действует не скомпенсированная сила : Fp=S*P=S*q*g*h. Fа : Fp=2:1 Выводится это следующим образом. Fа=G*V =(V*S*q) V= S*q *V^2 Скорость струи и давление подчиняется равенствам: Где Рh- давление столба воды высотой h с плотностью q при ускорении свободного падения g, Pv- скоростной напор той же воды. Так как в отверстии верно равенство Pv=Ph, то верно равенство: q*g*h=V^2*q/2 откуда V^2=2*g*h Подставляем выражение для V^2 в формулу Fа и получаем: На противоположную от отверстия стенку бака действует гидростатическое давление: При этом на площади проекции отверстия действует нескомпенсированная сила гидростатического давления : ИТОГО: Сила Fp от давления на площади отверстия равна: Fp=(q*S*g*h) Откуда: Fа:Fp = 2:1 В рамках гидравлики данный парадокс толком качественным образом не объясняется , сводя всё к расчётам с использованием коэффициентов местных сопротивлений на входе потока жидкости в отверстие в стенке бака.(см.таб.Рис.14) Рис.13. Схема истечения жидкости из отверстия в стенке сосуда. Рис.14. Таблица характеристики местного сопротивления на входе в отверстия в резервуаре из-под уровня жидкости. Рис.15. Вид коноидального насадка на воздухозаборе газотурбинного двигателя, установленного для наземного испытания на неподвижном стенде с нулевой скоростью полёта. Насадок чуть шире штатного обтекателя турбины, но уже позволяет избежать сильного поджатия струи сбоков при плавном заходе боковых потоков воздуха в отверстие. Рис.16 Коноидальный заход на авиационном турбо-вентиляторном двигателе, устанавливаемом на стенд для наземных испытаний. В реальной гидравлике существуют сопротивления и потери, поэтому величина отличия двух величин сильно зависит от формы краёв отверстия. Так разная форма захода потока в отверстие снижая эту чёткую двойку до диапазона значений Fa/Fp=1,3-1,96 (см.таб.Рис.13) Рh=0,53*Pv+Pv=(0,53+1)*Pv=1,53*Pv Откуда: Pv=Рh/1,53=0,65*Ph то есть потери входа составляют 35% от давления в сосуде, при этом Fa/Fp=1,3 . Pv=Рh/1,02=0,98*Ph То есть потери входа в коноидальный насадок (см.рис.13,15-16) составляют всего 2% от давления в сосуде. Попытка решить парадокс за счёт учёта местного сопротивления на заужение струи в отверстии (см.рис.13) не является решением парадокса, так как коноидальный и конический заходы дают столь малые потери напора на входе, что обеспечивают практически 2-х кратный разрыв (без 4%) в расчётных значениях «тяги сопла» в явном виде. Решение парадокса об избытке тяги в струе из бака под давлением. Рис.17. Форма поверхности в стакане с вращающимся чаем. Рис.18. Разложение сил на поверхности в стакане с вращающимся чаем. Дополнительную тягу в коноидальном насадке в стенке бака с водой создаёт разрежение над коноидальной поверхностью, так как над ней проносится изогнутый слой воды, создающий центростремительное ускорение за счёт разности давления под уровнем и в пограничном слое у стенки коноидального насадка. Именно эта разница давлений по сторонам водяного потока создаёт центростремительное ускорение и искривляет поток. Пи*(R+r)^2=Пи*2*R^2 Откуда : r=(2^0,5)R-R=(2^0,5-1)R=0,414R или приблизительно r=0,2D То есть радиус скругления идеального коноидального захода сравнительно мал и составляет всего 20% диаметра основного отверстия. Удвоенная тяга от реактивной струи при вытекании из отверстия в сосуде под давлением, а также формула подъёмной силы крыла от изгибаемого потока позволяет решить загадку «вертушки Феймана» в режиме всасывания. Рис.19. Вращение газонного разбрызгивателя типа «вертушка Феймана» в прямом направлении. Вращение вертушки-разбрызгивателя в прямом направлении с выбрасыванием воды (см.рис.19) легко объяснимо, так как на конце трубки струя воды создаёт реактивную тягу: Fт=G*V=(q*S*V)*V=q*S*V^2 Но почему вертушка перестаёт вращаться в режиме всасывания при погружении в воду? Оказывается, что при обращении потока на конце трубки возникает всасывающая сила, аналогичная тяге на коноидальном насадке при истечении из бака под давлением. Fs=2*S*Pv=2*S*(q*V^2/2)=q*S*V^2=G*V При этом сила Fs направлена вдоль потока, но против скорости потока внутрь трубки. Рис.20. Схема потоков воды, сил и давлений в «вертушке Феймана»: А- при прямом потоке (разбрызгивание); Б- при обратном потоке (всасывание). Расчёт этой силы Fт в качестве «подъёмной силы крыла» мы производили в первой главе статьи по «аэродинамике». Итог расчёта таков: Где dH-толщина изогнутого потока, В-ширина изогнутого потока, R-радиус кривизны загиба трубы. V-cкорость воды в трубе, q- плотность воды в трубе. Причём для рассматриваемой трубы произведение dH*B=S трубы. Подставляя первую формулу для Рт во втору для Fт получаем: Fт= Р*т*B*R=dH*q*(V^2/R)*B*R Сокращая одноимённые R и подставляя выражение S получаем: Fт= dH*q(V^2/R)*B*R = dH*В*q*(V^2) = S*q*(V^2) Так как G=S*q*V , то подставляем в формулу и получаем Fт= S*q*(V^2) = ( S*q*V)*V = G*V То есть для реактивной центростремительной силы от потока в трубе при повороте мы получили выражение Fт=G*V , тождественное к формуле реактивной тяги струи из отверстия. Так мы получили весьма нетривиальный результат! Оказывается, что реактивная тяга струи создаётся вовсе не на срезе отверстия, из которого струя вылетает, а где-то в недрах трубы на каких-то загибах водяного потока. ИТОГО: При обратном направлении работы вертушки в режиме всасывания Fт=Fs (по модулю) и направленны противоположно, взаимно компенсируя друг друга, что и не даёт вертушке крутиться. В прямом направлении вращения вертушки тяга Fs трубки тоже есть (нагнетание в трубку из шланга), но находится она на оси вращения вертушки (где шланг крепится). Таким образом силы от нагнетания воды в трубку от оси вертушки не создаёт крутящего момента на трубке относительно оси вращения вертушки, так как при нагнетании воды в трубку сила Fs направлена по радиусу от оси вращения вертушки. Получается, что сила тяги на изгибе трубки Fт присутствует всегда и пытается вращать трубку вертушки в одном и том же направлении, независимо от направления потока воды в трубке (выброс или всасывание). При этом сила той же величины Fт=Fs на одном из всасывающих концов трубки может как компенсировать силу тяги Fт и тем самым останавливать вертушку (при всасывании), или не будет на неё влиять при нулевом рычаге относительно оси вращения вертушки (выброс воды из вертушки). Гидравлические потери по длине трубки не учитываем. Это позволяет записать Р=0 в трубке при прямом вращении (выбрасывание струи). При этом поперечное динамическое центростремительное давление на изгибе трубки носит локальный характер и не оказывает влияние на течение жидкости вдоль прямой трубы. Избыточное давление P в вертушке целиком расходуется на первоначальный разгон воды на входе в трубку (см.рис.17-А) , при этом: Р=Рv , где Pv=q*V^2/2. Таким образом мы получили чёткое силовое обоснование отсутствие вращения вертушки Феймана в режиме всасывания. Вопрос: А для чего вообще мы рассматривали «вертушку Феймана»? Ответ:
Принцип передачи силового воздействия к изогнутой стенке от изгибаемого ею потока без изменения скорости потока по модулю широко используется в гидро-газодинамике как в водяных и газовых турбинах, так и в РД с различными типами сопел: штыревыми, тарельчатыми, плоскими (см.рис.21). Рис.21. Различные виды сопла ЖРД: а-Тарельчатое, б-плоское или штыревое (в разрезе у них вид одинаковый), в-сопло Лаваля. Применение типов а-б связано с компактностью сопел, что важно для некоторых типов ракет (чаще военного назначения). Разобравшись с механизмом работы коноидального насадка на выходе потока из бака под давлением можно продолжить разбор работы КС ЖРД. На срезе критического сечения КС (и срезе сопла) начинает действовать «великий интегратор»- закон импульса силы Ньютона: F=m*a= m*dV/dt= d(m*v)/dt. То есть на срезе критического сечения КС становится абсолютно всё равно, что происходило с газами внутри самой КС, а тягу определяет однозначное произведение массового расхода на реальную продольную скорость истечения этих газов Fкр=G*Vкр. При выстраивании силового баланса в работе ЖРД нужно куда точнее измерять скорость струи в критическом сечении КС, чем это отображается на графиках параметров газа в тракте ЖРД (см.рис.2-3). На критическом сечении графики давления и температуры становятся почти вертикальными, теряя точность в привязке к критическому сечению. Fa =124% от Fр. Нам известно, что 24% приращение тяги связано с двукратностью импульса силы Fa по отношению к силе Fр-кр по площади критического сечения от реального динамического давления Pv-кр (скоростного напора струи газов) на срезе КС. 0,62*Ркс=qкр*Vкр^2/2 Для сохранения силового баланса в КС где-то надо найти потеряные 38% от давления Ркс на выходном конце КС. Получается, что газовая струя преодолевает критическое сечение КС с большим запасом энергии, сосредоточенной в высоком давлении и остаточной температуре газов. Расчёт скорости газов в критическом сечении КС исходя из известной плотности газов и известного импульса тяги ЖРД в критическом сечении КС. Рис.11. Расчётные формулы из учебника. Посчитаем расширение газа от зоны горение топлива в КС до критического сечения через уравнение адиабаты: Ркс/Ркр=(qкс/qкр)^1,15 qкр=((9,84)^1,15 * 5740000 / 10000000)^(1/1,15)=6,0723кг/м3 То есть данные зависимости из учебника (рис.10) вполне воспроизводимы по расчётным формулам. Ркр=0,574*100=57,4атм Температуру в КС считаем 3800К, что даёт температуру в критическом сечении: Ткр=0,93* 3800 = 3534 К Плотность газов в КС получаем из молярного объёма газа при давлении 10МПа и температуре 3800К: Vm=RT/P=8,31* 3800 / 10000000=0,00315 м3/моль При молярном весе 0,031кг/моль для смеси газов (СО2+Н2О) в равных объёмах плотность составляет : Давление в критическом сечении равно: Зная плотность газов в критическом сечении КС можно получит скорость Vкр из уравнения тяги: 1,24*Ркс=qкр*Vкр^2 Откуда Vкр=(1,24*Ркс/qкр)^0,5=(1,24*10000000/6,07)^0,5=1429м/с Итого по расчёту №2: Vкр=1429м/с при плотности газов qкр=6,07кг/м3. Полученная скорость Vкр=1429м/с прекрасно укладывается в предложенную ранее модель с отличием скорости фронта звуковой волны от максимальной скорости молекул во фронте волны. Vа=(1,15*8,31* 3534 /0,031)^0,5=1043м/с То есть Vкр-м отличается от Vкр в 1470/1429=1,029 раза или на 2,9%. Если посчитать плотность газов в критическом сечении КС по скорости звука Vа=1043м/с, то плотность получится несуразно большой: qкр=1,24*Ркс/( Vкр^2)=1,24 * 10000000/(1043^2)=11,39 кг/м3 Получилось, что плотность газов в критическом сечении qкр= 11,39 кг/м3 превосходит плотность газов qкс= 9,84 кг/м3 при Ткс=3800, что невозможно при разгоне газов в критическом сечении КС за счёт своего расширения. Таким образом расчётная «скорость звука» никоим образом не применима для расчёта тяги в критическом сечении КС ЖРД. Первый крупный смысловой разрыв в теории ЖРД Тут возникает первый крупный вопрос о правильности формул и конечных цифр в теоретических формулах из учебника. Vмах= (Ет*2/Мтоп)^0,5 = (40 570 000*2/3,7)^0,5 = 4682 м/с Правда, в учебниках приводится цифра скорости 3599м/с при равновесном расширении для кислород-керосиновой пары с отношением (3,07:1). Но я не готов принять эту цифру, так как кинетическая энергия такой струи составляет всего 65% от теплотворной способности керосина при сгорании. На основании этого струя из КС должна иметь скорость: Vкс-мах =Vмах*0,4936 = 4682*0,4936 = 2311м/с Если в реальном ЖРД (см.рис.3) на срезе сопла скорость 3400м/с (в вакууме), то доля тяги КС реального ЖРД составит: Fкс / Fжрд = 2311/3400 = 0,679 или 68% А доля энергии срабатываемой на КС составляет: Ек-кс/Ек-жрд =(Vкс/Vжрд)^2=(2311/3400)^2=0,462 или 46% Из этого энергобаланса становится понятно почему развитой сопловой частью стали оснащать ЖРД только на крупных орбитальных РН, где по формуле Циолковского борьба за прибавку скорости газов из сопла ЖРД имело первостепенную важность: Vрн= Vжрд * ln(M/m) При этом в боевых низкоскоростных баллистических ракетах и ракетах оперативно-тактического назначения, летающих не очень быстро и в плотных слоях атмосферы, сопла имеют малое расширение, используя только максимально плотную начальную фазу расширения газов из КС. Критерием для такого снижения КПД РД тактических ракет (чаще твёрдотопливных, а не жидкостных) является снижение общего габарита ракеты, чтобы помещалось больше боеприпасов в ограниченном объёме отсеков самолётов или транспортных машин, а сами ракеты стоили дешевле в производстве. (см.рис.22-23) Рис.22. Разрез реактивного неуправляемого снаряда. Под цифрой (6) указан реактивный двигатель, состоящий из следующих элементов: конический заход из КС на критическое сечение, короткое цилиндрическое критическое сечение, коническое сопло. Интересно , что коническое сопло всего в 2 раза шире критического сечение (Fa/Fкр=4-4,5), а паралельная работа нескольких малых РД позволяет сократить длину РД в целом при неизменной его мощности (силе тяги). Рис.23. Разрез оперативно-тактической баллистической ракеты «Искандер». Первая ступень имеет развитое сопло с изменением диаметра в 4 раза от диаметра критического сечения, что определяет необходимость эффективного разгона для увеличения дальности ракеты в целом. Вторая ступень имеет в два раза меньшее по диаметру сопло, что снижает эффективность ТРД, но с учётом малого размера 2-й ступении экономия массы на укороченом сопле с избытком компенсирует потерю эффективности ТРД на коротком разгоне конечного участка полёта. Пересчитаем параметры ЖРД под новую скорость Vкр=2311м/с. 1,24*Ркс=qкр* Vкр^2 Откуда qкр = 1,24*Ркс /( Vкр^2 )= 1,24* 10000000 / (2311^2) = 2,321 кг/м3 Из полученной плотности можно посчитать давление в струе газов на срезе КС по уравнению адиабаты: Ркр = 10/(9,84/2,321)^1,15=1,899 МПа Подставляя полученное Ркр в уравнение газового состояния получаем и температуру: Ткр=1899000*(0,0224*1,38 / 2,31)/8,31=3058К То есть в КС срабатывается дТкс= 3800-3058=742К Или Екс/Ежрд=742/(3800-1800)=0,371 или 37% полезной кинетической энергии из ЖРД, при Vсоп=3400м/c. Опять проявилась расчётная неувязка, если учесть что ранее была получена Екс/Ежрд большей величины, а именно: Екс/Ежрд= (2311/3400)^2 = 0,46 или 46% То есть температура газов из КС должна быть ещё ниже, а именно дТкс=0,462000=920К. Тогда Ткр=3800 — 920= 2880К. Если мы не сомневаемся в полученых значениях плотности газов qкс=9,84 и qкр=2,32кг/м3, то следовательно требуется корректировка величины давления Ркр. При Ткр=2880К давление будет Ркр=2880* 8,31/ (0,0224* 1,38 / 2,31)=1 788 456 Па =1,79 МПа путём подгона коэффициента адиабаты получаем нужное равенство при к=1,1914 : Ркр = 10 / (9,84/2,321)^1,1914 =1,789 МПа Интересно, что нужную нам Ткр=2880К по энергетическому балансу в КС ЖРД можно получить при расчёте температуры по формуле из учебника с показателем адиабаты к=1,639 : Ткр=Ткс*2/(к+1)=3800* 2 / (1,639+1)= 2880 К В случае работы ЖРД в плотных слоях атмосферы с давлением на срезе сопла Рсоп=0,1Мпа (1атм) Fкс / Fжрд=2311 / 3100 =0,745 или 75% В формуле постоянного массового расхода G плотность и скорость друг с другом жёстко связаны: При этом саму величину G определяет сам двигатель в исходных данных, и мы его изменить не можем, не нарушив условие неразрывности потока. G=qкрVкр=6,07 * 1429=8674 (кг/(с*м2))— по формулам КТГ из учебника. G=qкрVкр=2,321 * 2311=5363 ( кг/(с*м2)) — по термическому балансу и законам Ньютона Разночтения в массовых расходах G по разным методикам подсчёта составляют отношение: 8674/5365=1,617 или около 62%. F=qкрVкр^2=6,07*1429^2=12 395 188 Н/м2 — по формулам КТГ из учебника. F=qкрVкр^2=2,321*2311^2=12 395 813 Н/м2 -по термическому балансу и законам Ньютона При этом силы тяги Fкр у нас совпали (их мы приняли изначально одинаковыми в качестве исходных данных). Итого по расчёту №3: Расчёт параметров струи в сопле Лаваля. Кv=Vкр/Vсоп= 3400 / 2311= 1,47 раза при разгоне от 2311 до 3400м/с ; геометрический рост сечения сопла 18,86 раза ( справочно для РД-107); начальная плотность q=2,321кг/м3 на срезе КС. Тсоп=1800К ( с графика рис.3) В итоге мы получим параметры на срезе сопла: q, . Исходя из предыдущих выкладок нам известно что при постоянном расходе по сечению G элементарный объём dW имеет связь с параметром скорости и плотности зависимостью: G=dW*q=const Так как кратность изменения геометрия слоёв dW нам известна (по росту сечения и росту скорости для РД-107), то можем посчитать параметр q среза сопла: qcоп=qкс / ((Vcоп/Vкр)* (Scоп/Sкр)) = 2,321 / (1,47*18,86)=0,084кг/м3 Исходя из полученой плотности можно получить молярный объём Vm, а из него посчитать давление газов, зная конечную температуру Тсоп=1800К: Vm-соп=(0,0224 * 1,38 / 0,084)=0,368м3 Р=R*Т / Vm = 8,31 * 1800 / 0,368 = 40 646Па или 4,06кПа = 0,0406 атм. Откуда проверочный расчёт по температуре сопла: Тсоп=PVm/R=40646* (0,0224 * 1,38 / 0,084) / 8,31=1800К Теперь зная конечные и начальные состояния газа можно получит показатель адиабаты для сопла Лаваля в РД-107 со стартовым давлением Ркр=17,9 атм на срезе КС , который при подгоне получается k=1,405: Ркр=Рсоп * (qкр/qсоп)^1,1405 =0,0406* (2,321 / 0,084)^1,1405 =1,788 атм. При подгоне под давление 17,9 атм в критическом сечении КС получен показатель адиабаты к=1,1405 для сопла Лаваля в РД-107, что уже лучше соответствует табличному показателю к=1,15, чем ранее посчитаный для КС показатель к=1,639. То есть приняв за исходные данные физические законы механики нам удалось свести приемлемый энергетический баланс с учётом законов термодинамики. С фактами и физикой-механикой я спорить не готов, а вот к формулам КТГ в быстротекущих неравновесных процессах у меня доверия нет. Так что примем для расширения в сопле Лаваля коэффициент адиабаты k=1,14 при Ркр=17,9 атм и Vкр =3211м/с, а затем посмотрим куда это нас приведёт в дальнейшем. Рассмотрим происходящее в сопле Лаваля на уровне отдельной молекулы газа в её элементарном объёме по теории СТГ. Vст-соп = Vкр * sin(Асоп) Где Асоп- угол стенки сопла к оси ЖРД. Таким образом уже на самой кромке критического Сечения КС у частиц газа в струе возникает дополнительная перпендикулярная составляющая к скорости потока в критическом сечении КС. Суммарная скорость молекул газа на границе конуса возмущения составит ( по теореме Пифагора): Vкон-кс= ( Vкр^2+Vст-соп^2)^0,5 Где Vст-соп- это скорость отступания стенки сопла в радиальном направлении от потока по оси ЖРД на скорости Vкр. Зона постоянного давления в сопле сохраняется на начальной конусной части сопла до момента полного срабатывания конуса постоянного давления газов из КС на оси ЖРД. Рис.24. Схема сечения ЖРД с указанием скоростей в разных сечениях. Рис.25. Схема распределения элементарных объёмов (плотностей газа) и скоростей молекул газа в ЖРД. На рисунке вектора скорости по сечениям показаны в масштабе, который определяет условное соотношение толщин элементарных объёмов dW по тракту ЖРД и скорости потока по сечениям ЖРД. Номерами на рисунке Б обозначены: 1-жидкое топливо; 2-газ в КС в широком сечении с максимальной температурой; 3-газ КС с максимальной скоростью при кинематическом разгоне ( с постоянной плотностью) перед критическим сечением; 4- газ в критическом сечении с Vкр; 5-газ на срезе сопла с минимальной плотностью при максимально скорости Vсоп. При завершении поворота потока от конического сужение в КС на цилиндрическое течение в самой узкой части коноидальной поверхности критического сечения КС происходит формальный переход от КС на расширение в сопле Лаваля. Рис.26. Разрез одной камеры РД-107 (РН типа «Союз») с рабочим давлением 60атм в КС. Хорошо заметно резкое заужение в критическом сечении КС. В данном случае большая по объёму КС выполнена для обеспечения более спокойного и стабильного режима горения топливной смеси на меньших скоростях движения на большем протяжении КС. Интересно, что длина КС больших и маленьких ЖРД на фото одинаковые, тогда как длина сопел пропорциональна поперечному сечению КС. То есть длина КС ЖРД не масштабируется с изменением мощности, так как определяется режимом горения топлива, а не мощностью ЖРД в целом. Поведение газов в КС на сужении. V3 / V1 =6,25*4,24 = 26,5 раза Учитывая квадратичность кинетической энергии от скорости и 26 кратный рост скорости от V1 до Vкр получаем, что до сужения КС кинетическая энергия газов в 700 раз меньше, чем конечная кинетическая энергия струи в критическом сечении на скорости Vкр (или Ек-s1=0,15% от Ек-кр). Можно сказать, что при перепаде дТ= 920 К на струе газов в КС при разгоне погрешность в менее 0,15% или дТ=1,4К можно считать несущественной для описания физики процесса. Скорость жидкого топлива в донной части КС qcр=(810+ 1141*2,7) / ,7=1051кг/м3 Тогда в донной части КС, где впрыскивается жидкий кислород и жидкий керосин со средней плотностью около 1051кг/м3, при таком же постоянном массовом расходе G средняя скорость топливной смеси составит всего Vо=879,84/1051=0,81м/с. То есть график скорости потока в КС ЖРД будет практически неотличим от нуля в масштабе изображения (см.рис.3), пока газы не дойдут до горячей зоны КС с максимальной температурой Ткс=3800К и до геометрического разгона суживающейся части КС. Поведение газов в критическом сечении КС ЖРД Разница площадей сферического и плоского слоя при постоянном массовом расходе дают резкий скачёк скорости в сравниваемых сечениях S1,S2 и S3. V3* S3* q3=V1* S1 * q1 Откуда Геометрические величины конфигурации КС будут нами сняты с условной геометрии по фото разреза ЖРД РД-107. При том, что величину G=V1*S1*q1=V0*S0*q0, можно взять из любого сечения КС. Площадь S2 на границе примыкания конического сужения КС к коноидальному сопряжению с соплом зависит от угла образующей конусной части КС. S1/S2= (Д1/Д2)^2= 2,2^2=4,84. Откуда V2=V1* S1/S2= 87*4,84=421м/с Изменение кинетичской энергии между сечениями S2 и S3 cоставляет отношение: Ек-s2/ Ек-s3=(V2 / V3)^2= (421 / 3211)^2=0,0179 или 1,8% Таким образом изменением давления и плотности между сечениями S1 и S2 можно пренебречь, а всю газодинамику рассматривать на участке коноидального захода и самом критическом сечении. При этом площади кругов сечений начала и конца коноидального захода относятся ка. S2/S3=(Д2/Д3)^2=(92/69)^2=1,26^2=1,59 Где Д2/Д3=92/69=1,26 — это оценочный замер с фото РД-107 (см.рис.26) Тогда площади сферической поверхности крайнего конического сечения S2 будет давать с площадь плоского критического сечения S3 соотношение: S2/S3=(S2/S2-0)*( S2/S3)=1,11 * 1,59=1,76 Получается, что на коноидальном сопряжении в КС скорость увеличивается в 1,76 раза только за счёт резкого изменения кривизны и диаметра сечений. Vкр / V2= 3211 / 421= 7,62 раза. При этом расчёт последовательного геометрического разгона и последующего линейного расширения даёт отношение : (S2/S3)* (qкс/qкр)=1,76* (9,84 / 2,321) = 7,46 Получились весьма схожие цифры между 7,62 / 7,46= 1,021 или разница 2% qкс/qкр=9,84 / 2,321 = 4,84 раза. происходит исключительно на цилиндрическом участке критического сечения, мгновенно выстреливая молекулами в сторону низкого давления в сопле за счёт внутренней энергии самих молекул газа. То есть для коноидального захода от конуса КС на цилиндрическое критическое сечение в расчётной модели вполне можно предположить , что сначала газ при постоянной плотности чисто геометрически разгоняется от V2=421м/с до скорости V3=421*1,76=741м/с. И эта скорость V3=741м/с даёт долю всего 5,3% от конечной кинетической энергии КС: (V3/ Vкр)^2 = (741 / 3211 )^2 = 0,053 или 5,3% Таким образом, вся сложная газодинамика КС с резким адиабатным расширением и разгоном газов может рассчитываться так, как-будто расширение протекает на коротком участке цилиндрической части критического сечения с погрешностью по энергобалансу менее 5%. Зона разрежения в КС на коноидальном заходе (R+r)^2=1,24* R^2 Откуда r=((1,24)^0,5 — 1)*R = 0,11*R То есть 24% прибавки тяги обеспечивается кольцом вокруг отверстия шириной всего 5% от диаметра Д3 отверстия S3 в критическом сечении КС. ИТОГО по разгону газов в коноидальном заходе от КС на критическое сечение: Может тогда и критическое сечение не нужно? Почему бы не делать КС в виде цилиндра с раструбом сопла на сверхзвуковой части? Собственно ради этого вопроса, по большей мере, и была затеяна эта статья. Ответ на вопрос состоит из двух частей: Ответ-Часть 1. На самом деле критическое сечение КС и так является прямой трубой для свободного разгона до предельной скорости в одном направлении, только очень короткой. Для лучшего понимания механизма почти мгновенного разгона до Vкр от V3 можно представить себе стенку с мелкими отверстиями, равными элементарной площади одной грани единично- молекулярного объёма газа. Fм=Ркс*Vмол^(2/3)=Ркс*(0,0224м3 / Nа* q/qмол)^(2/3) где qмол- плотность газа в нормальных условиях. При этом масса одной молекулы составляет Mм= Mr*Vмол * q/qмол= Mr* (0,0224м3/Nа) * q / qмол Подставляя эти две бесконечно малые величины разных порядков в закон Ньютона F=ma получаем: а=Fм / Mм= (Ркс*(Vмолq/qмол )^(2/3)) / (Mr *( Vмол* q/qмол)) Сокращая одноимённые множители в числителе и знаменателе получаем: а= Ркс/ ( Mr * (Vмол* q / qмол) ^(1/3) ) Учитывая крайнюю малость величины: Vмол=0,0224 м3 / Nа=0,0224 / (6,02*10^23) =3,7 / (10^26)м3 То даже кубический корень из неё останется бесконечно малой величиной: Lмол=Vмол^(1/3)= 3,34 / (10^9)м Подставляем эту чудовищно малую величину в выражение для ускорения и получаем гигантское до невообразимости ускорение: а= Ркс/ ( Mr (Vмолq /qмол) ^(1/3)) a=10 000 000 / (0,031*(3,7 / (10^26)*10/1,38)^(1/3))= 5*10^16 м/с2 Разделив эту цифру на величину g=9,81 м/с2 получим ускорение в более привычных величинах: Словами эта цифра звучит так : « Пять тысяч триллионов Ж» Ответ-Часть 2. При смене точки зрения оказывается, что это КС расширяется, а не «выхлопная труба» сужается. Новая КС будет представлять из себя полушарие, где расположением форсунок впрыска топлива осуществляется по поверхности полусферы, а коноидальный заход на критическое сечение будет расположен по центру плоского среза полусферы.(см.рис.27) Но не экономия места главное качество сферической КС! В сферической КС нет наружных перегретых стенок! Получается что вся наружная поверхность сферической КС закрыта форсунками и подводящими камерами с холодным топливом. Рис.27. Сравнение габаритов ЖРД с КС разной формы, но одинакового объёма, при одинаковых массовых расходах топлива G и при одинаковом давлении Ркс: Участок коноидального перехода оказывает максимальный вклад в формирование дополнительной тяги КС от пониженного давления в сужении КС, нескомпенсированного постоянным максимальным давлениям на дно КС. Рис.28. Варианты захода на критическое сечение КС с плавным коноидальным заходом и с ломаной образующей на конус с малым углом конуса. Замена коноидального перехода на резкий излом в сопряжении конуса КС и критического сечения приведёт к появлению виртуального критического сечения меньшего диаметра в самой сужающейся по инерции струе газов, по аналогии с поджатием струи воды в отверстии бака под давлением. Если учесть сильное отличие поведения несжимаемой жидкости от сильно сжимаемых газов при предельно высоких околозвуковых скоростях, то у работы коноидального насадка в критическом сечении КС будут значительные особенности. Фактически коноидальное сопряжение КС и сопла носит технологический характер, снижая ударные нагрузки и тепловые нагрузки (перегрев острой кромки излома стенки) при срыве потока газов с острых кромок сопряжений. Плавное скругление в коноидальном сопряжении конусов КС и сопла обеспечивает размывание фронта звуковой волны поперёк оси ЖРД, тем самым обеспечивая более мягкий и устойчивый режим работы ЖРД. В предыдущих главах мы выяснили, что на критическом сечении КС уже достигнута максимальная скорость газов от сработки части давления газа вдоль оси ЖРД. Как адиабатное расширении тонких слоёв поперёк сопла даст приращения скорости газа в перпендикулярном к расширению направлении? Рис.29. Схема взаимодействия арочных молекулярных слоёв в прямоточном реактивном двигателе. А с чего вообще должны образовываться какие-то арочные-сферические слои в сопле РД? В расширяющемся коническом сопле постоянное по величине давление действует вдоль изогнутой поверхности сферического-арочного слоя, на каждой из молекул которого при этом создаётся перпендикулярная к поверхности слоя сила (см.рис.30-33). Рис.30. Схема упругих сил в слоях и между слоями на сужении в КС и расширении в сопле ЖРД. (разрез по оси). На схеме показана неравновесная работа упругих сил взаимного отталкивания в ускоряемых газах в различных частях ЖРД (по СТГ). При разгоне увеличиваются расстояния между арочными слоями в начале и в конце заужения КС на схеме. В сопле Лаваля происходит разгон газов в 1,5-2 раза от скорости газов на срезе КС до среза сопла, в такой же степени увеличиваются расстояния между арочными слоями в начале и в сопла на схеме. Рис.32. Схема сил отталкивания в сферическом слое, создающие разгонную силу на молекулах перпендикулярно слою. (поперечный разрез) Именно эта перпендикулярная к изобарному слою сила и разгоняет слой в перпендикулярном к его поверхности направлении. Ровно та же ситуация прослеживается в дозвуковой КС, где коническая сужающаяся часть КС должна производить работу над газом, тормозя его. Значит в КС на сужении надо рассматривать арочные слои с прогибом в сторону дна КС. (см.рис.31) Попытаемся найти этим предположениям подтверждения в существующих учебниках по теории работы ЖРД. Именно это нам и нужно было доказать! давление вдоль оси потока Ркр-о близкое к нулю ( равно давлению внешней среды) давление на стенки критического сечения поперёк потока Ркр-т= 18 атм (18% от максимального давления в КС, равного Ркс=100атм), которое фактически не регистрируемо инструментально из-за высокой кривизны и динамичного ускорения потока в критическом сечении КС. Указанное в расчётных формулах Ркр=0,574*Ркс (см.рис.11) относится не к критическому сечению КС, а к более глубокому сечению в конической части КС с меньшей в два раза скоростью газов, где ещё возможно замерять параметры на стенке, адекватные параметрам по всему сферическому слою данного сечения. По расчётные формулам из учебника (см.рис.11). Vа =(1,15* 8,31 * 3534 / 0,031)^0,5=1043 м/с Полученная скорость звука Vа =1043м/с в целых 2 раза ниже, чем получаемая в реальном ЖРД РД-107 скорость газов согласно замеряемой силе тяги КС и соответсвующей ей скорости при заданном постоянном массовом расходе G. Почему газы не могут разгонятся в сужающемся сопле выше некой фиксированной расчётной скорости, называемой «местной скоростью звука»? Какую долю энергии мы срабатываем на достижение расчётной «скорости звука-MAX» в критическом сечении КС РД? В итоге пришлось сильно откорректировать расчётные значения. Так при принятой Vкр=0,5*Vмах-беск=2311м/с замеряемая температура в критическом сечении составляет Т=2880К вместо Т=3543К с поперечным давлением Рт=18 атм (вместо 57 атм), при начальных в КС параметарах Ткс=3800К и Ркс=100атм. При принятии в качестве реальных исходных силовых данных значений из таблицы (рис.12), то при пересчёте термодинамических параметров получаем, что график(рис.3) нам достаточно сильно подвирает со скоростью, температурой и давлением в критическом сечении. Рис.34. Откорректированный график параметров газов в тракте ЖРД. Для понимания добавлено несколько линий связи разреза ЖРД с графиком для обозначения важных границ отдельных функциональных частей ЖРД. Конусная часть сопла заканчиваяется при срабатывании центрального конуса газов из КС. На графиках появились горизонтальные полки в зоне постоянного разрежения при срабатывании конуса газов из КС. Полную выработку энергии поля отталкивания молекул при быстром адиабатном расширение газа нужно обеспечивать при одновременном расширении в три ортогональных стороны (то есть в трёхмерном пространстве), а не как в общепринятом медленном поршневом двигателе в одну сторону от поршня цилиндра. Численная оценка сил и ускорений в арочных слоях в сопле Лаваля. дL=(Vm / Nа)^(1/3) Где Vm- молярный объём в данных условиях, Nа-число Авогадро (количество молекул в 1 моль вещества) Сила Fтс=6*Fс* sin(Ам) Где множитель 6- это количество ближайших соседних молекул в сферическом слое к одной рассматриваемой молекуле, SinАм- отношения половины растояния между молекул в сферическом слое к радиусу кривизны слоя в этом месте, а сила Fc приближённо может быть расчитана как давление газа Ргаз отнесённое на элементарную грань шестигранной или квадратной призмы элементарного объёма молекулы. Fc=Ргаз*dL^2=Ргаз((Vm/Nа)^(1/3))^2=Ргаз*(Vm/Nа)^(2/3) Величина угла Ам =sinАм при малых углах равна sinАм=0,5*дL/Rсл=0,5*(Vm/Nа)^(1/3)/Rсл Ускорение молекулы составит а=F/m=6* Fс* sinАм/ (Mr/Na) а= (6*Fс*0,5*(Vm/Nа)^(1/3)/Rсл)/ (Mr/Na)=(3*Fс*Na*(Vm/Nа)^(1/3)) / (Rсл*Mr) Дробные степени суммируются при перемножении их одинаковых оснований , таким образом показатели степени 1/3 и степени 2/3 при элементарном объёме (Vm/Nа) складываются, становясь единицей: а=(3*Ргаз*(Vm/Nа)^(2/3)*Na*(Vm/Nа)^(1/3)) / (Rсл*Mr) а=(3*Ргаз*(Vm/Nа)*Na) / (Rсл*Mr) В результате преобразования число Авогадро Nа оказалось как в числителе , так и в знаменателе, что привело к его взаимному сокращению и выпаданию из формулы совсем: а=3*Ргаз*(Vm/Nа)*Na / (RслMr)=3*Ргаз*Vm/ (Rсл*Mr) Итого: Ускорение молекулы в сферическом слое в сопле Лаваля равно: а=3*Ргаз*Vm / (Rсл * Mr) Так как произведение Ргаз*Vm=R*T, то ускорение можно выразить и через одну температуру: а=3*Ргаз*Vm/(Rсл*Mr)=3*R*T/(Rсл*Mr) То есть динамика разгона зависит только от переменных температуры и кривизны слоя. Уже поверхностный анализ показывает, что ускорение будет огромной величиной, так как в числителе присутствует большое число от произведения RT, а в знаменателе находятся малые величины радиуса и молярной массы ( для продуктов сгорания ЖРД Mr=0,031кг/м3), что ещё больше увеличивает конечное ускорение молекул в сферическом слое. Считаем , что величины входящие в формулу равны: Rсл=2Dкр=0,4м (непосредственно за выходом из КС в сопло) а=3*R*T/ (Rсл*Mr)=3*8,31*3500/ (0,4 * 0,031) =7 036 693 м/с2 При таком ускорении скорость 3400м/с будет достигнута за время: дt=3400 / 7036693 = 0,00048с При этом молекулами газа при таком ускорении будет пройдено расстояние: L=3400* 0,00048 / 2= 0,816м Цифры вполне согласуются с формой и размерами реальных ЖРД . В тоже время в самой КС кривизна сферического слоя давит в обратную сторону, то есть внутрь КС, тем самым создавая избыточное статическое давление внутри КС. В то же время в основной части КС скорость газов столь мала, что разгон газов в конической части КС происходит как у несжимаемой жидкости, а подсчёт скорости по сечениям КС производится исходя из постоянноого массового расхода при постоянной плотности газа, то есть чисто геометрическими методами. Резкое расширение газов в сопле Лаваля создаёт давление на стенках сопла, имеющих проекцию на ось ЖРД. Сопло Лаваля — это не единственная возможная форма сопла. Рис.35. Плоское дисковое сопло для РД. А. Схема переноса слоёв с узкого конического ориентированого сопла на плоское сопло. Б. Схема слоёв расширяющихся газов в дисковом сопле. Тут возникает только вопрос с КПД такого плоского сопла. Будет ли оно выше, чем у обычного направленного сопла? Площадь полусферы: Sсф/2=2*R^2 * 3,14 А площадь круга: Sкр= R^2 * 3,14 То относится КПД плоского и направленного сопел будут как: Sкр : Sсф/2 = 1:2 =0,5 То есть КПД плоского сопла будет почти в 2 раза ниже, чем КПД узкого направленного сопла. В рамках описаной модели ЖРД по СТГ становится понятным стремление к подъёму давления в КС при сохранении неизменной температуры (скорости струи) на критическом сечении КС. Так при большем давлении на одинаковой скорости потока можно пропустить тот же массовый расход G через сечение меньшей площади. То есть получается более компактная КС, или кратно большая мощность при неизменных размерах. При этом для расширения в сопле Лаваля остётся больший диапазон разрежения до уровня внешнего давления подпора атмосферы. Рис.36. Фото,разрез и чертёж одной камеры РД-180 с рабочим давлением 250атм в КС. Хорошо заметно резкое заужение в критическом сечении. КС выглядит явно «маленькой» по сравнению с большим по размеру соплом с высокой кратностью расширения. Интересно отметить, что рост мощности отдельной КС ЖРД остановился на уровне тяги 200 тс при давлении в Ркс=250атм ещё 50 лет назад на двигателях типа РД-170. Рис.37. Разрез камеры ЖРД F-1 от ракеты Сатурн-5. Виден плавный переход с малым заужением от КС к критическому сечению. Также видна малая степень расширения в сопле Лаваля, что говорит о достаточно низком остаточном давлении в струе газов после критического сечения КС. Рис.38. Фото внутренней стороны сопла ЖРД F1 от РН Сатурн-5. Виден малый перепад сечения КС на заужении критического сечения. рис.39. Испытания ЖРД F-1 на стенде. Хорошо видно тёмный поток несгоревшего топлива по краю потока газов из сопла. Несгоревшее газообразное топливо резко воспламеняется от контакта с кислороом воздуха далеко за краем сопла. Рис.40. Фото запуска РН Союз с двигателями РД-107. Пламя из сопла на столько прозрачное, что на фото сквозь струю газов из сопла видна дальняя кромка этого сопла. При этом слой холодного газа из несгоревшего керосина-охладителя тоже есть, именно это топливо на периферии струи вспыхивает ярким непрозрачным пламенем уже далеко после вылета за края сопла. Библиография: Яскин, А.В.
Проблема где-то есть, и она находится где-то в недрах как самой КТГ, так и в термодинамической модели ЖРД.
Ниже приведена страница учебника по теории ЖРД (см рис.8-9), где в формуле (2.4) вместо коэффициента 3 или 10,77 приводится дробь из показателя адиабаты:
Кр=(к/(к-1))=(1,15/(1,15-1)= 7,667.
что даёт: Кр=(1,1/(1,1-1)=10,8
Получается, что для расчёта энергосодержания нам подходит коэффициент к=1,1, а для расчёта адиабатического расширения по конечным точкам температуры от 3800К до 2200К уже нужен к=1,134
Кстати, в учебнике по теории ЖРД (рис.9) ещё и не верно представлены размерности в формуле (2.4), так как в кинетической энергии почему-то потеряли массу одного моля летящего вещества Mr (молярную массу).

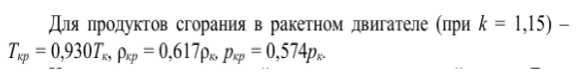
Прикладные аспекты создания РД- это область знаний, где за последние 80 лет развития ракетостроения было измерено и посчитано всё, что только можно измерить и посчитать.
В учебнике теории ЖРД [1] приводятся совершенно в явном виде цифры, которые говорят об отличии силы тяги РД в критическом сечении выше расчётной по давлению в КС на совершенно конкретную величину 22,8-24,8% (см.таб..рис.12).
Но сила реактивной тяги струи вовсе не давлением скоростного напора струи определяется, а импульсом массы выбрасываемой струи!
Сила тяги струи из сосуда но закону Ньютона F=m*a=d(mv)/dt оказывается аж в 2 раза больше, чем произведение площади отверстия на давление скоростного напора:
Fр=Sотв*Ркс
Этот парадокс физики с избытком тяги в отверстии сосуда под давлением достаточно хорошо известен ещё из курса физики-гидравлики. (см.рис.13)Парадокс о превышении тяги от струи из отверстия над нескомпенсированным давлением жидкости на площади отверстия
Это парадокс описывается так:
Через круглое отверстие в стенке сосуда вытекает струя воды.
Сила тяги импульса силы этой струи равна:
Fа=m*a=d(mV)/dt=G*V
Парадокс в том, что сила тяги импульса струи Fа превышает не скомпенсированную силу от давления жидкости на площади сечения отверстия Fp конкретно в 2 раза.
Массовый секундный расход жидкости G=VSq
Подставляем выражение для V и G в формулу для Fа:
Рh=q*g*h
Pv=V^2*q/2
Откуда при сокращении в обеих частях одноимённых величин плотности (q) получаем:
g*h=V^2/2
Fа= S*q V^2=S*q*(2*g*h)=2*(q*S*g*h)
Р=q*g*h.
Fp=S*P=S*q*g*h.
Реактивный импульс силы струи Fa равен :
Fа= 2*(q*S*g*h) 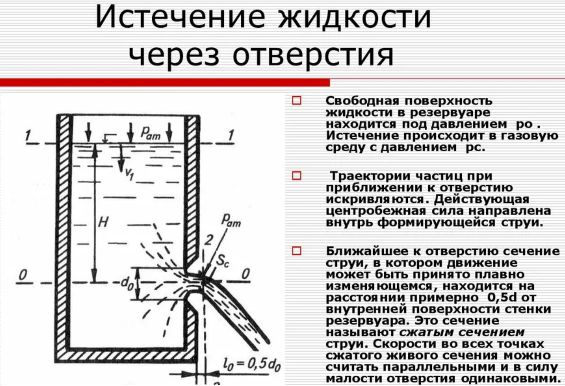
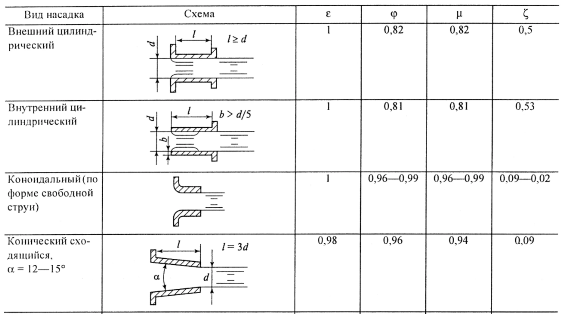


В таблице местных гидравлических сопротивлений разных форм отверстий в стенке бака для нас интересен последний столбец таблицы- это коэффициент сопротивления (потерь) входа в отверстие в долях от скоростного напора исходящей из отверстия струи.
Максимальный коэффициент потерь 0,5-0,53 при острых кромках на входе в трубу насадка (первые две строчки), с учётом которых получаеся следующая величина скоростного напора в сечении отверстия:
Минимальный коэффициент потерь 0,09-0,02 при плавном разгоне струи на входе (последние две строчки):
Именно две последние строчки дают наибольший разрыв в отношении Fa/Fp=1,96Решение парадокса об избытке тяги в струе из бака под давлением
Так откуда берётся избыток тяги в сосуде с дыркой и в ракетном ЖРД?
У феномена есть вполне физическое качественное объяснение, но его принятие потребует отказа от догмы аэродинамики и гидравлики, трактующих эффект «подъёмной силы крыла» через уравнение Бернулли.
Если отказаться от уравнения Бернулли и принять объяснения с центростремительными ускорениями и реакциями закруглённых стенок на протекающий мимо высокоскоростной изогнутый поток жидкости или газа (см.главу №1 данной статьи) и при согласии на существование разных давлений вдоль и поперёк потока (стакан с вращающимся чаем в гравитационом поле см.рис.17-18), то «чудо» избыточной тяги рассеивается как в случае с дырявым баком воды, так и в случае ракетного сопла.

Надо помнить, что конидальный насадок в потоке жидкости не создаёт эффективную форму потока, а скорее её сопровождает.
Таким образом поток жидкости над коноидальным насадком имеет нулевое давление, возможен даже режим пролёта потока жидкости над коноидальным насадком с тонким воздушным зазором (кавитация). Режим пролёта потока с воздушным зазором над изогнутой поверхностью является очень нестабильным, с резкой турболизацией и торможением потока при внезапном касании потока поверхности насадка.
Именно это нулевое нескомпенсированное давление над изогнутой поверхностью создаёт приращение тяги струи в 2 раза над статическим давлением в отверстии при пересчёте на наименьший диаметр отверстия насадка.
Из этого можно вычислит размер скругления коноидальной поверхности, так как площадь всего насадка в проекции должна быть ровно в 2 раза больше площади отверстия насадка:
Дополнительную тягу того же типа создаёт закруглённая выпуклая стенка на сужении КС в ЖРД, также имеющего вид коноидального (или конического) захода от конической КС на зауженное отверстие в критическом сечении.
Причём на заужаемой части КС в явном виде происходит (и регистрируется инструментально) падение давления (см графики на рис.3), которое на наклонных стенках сужения КС обеспечивает появление неуравновешенной силы в проекций на ось КС, не равной давлению на дно КС.Загадка «вертушки Феймана»

То есть мы нашли силу, которая должна была бы толкать трубку в обратную сторону!
Так почему трубка вместе с вертушкой не вращается?
Оказывается, что мы забыли учесть центростремительную силу от потока на изгибе трубки, которую ранее считали силой реактивной тяги в прямом направлении. При этом сила тяги на повороте трубки имеет всегда одно и тоже направление: из поворота наружу, не завися от направления потока воды по трубке (см.рис.20).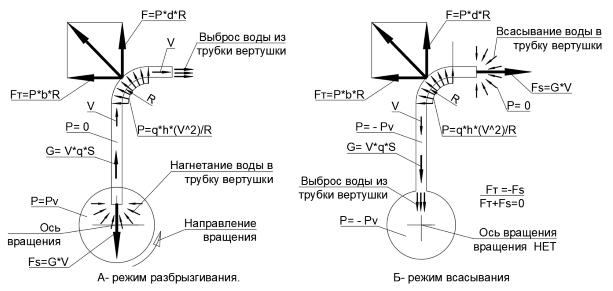
Рт= dH*q*а=dH*q*(V^2/R)
Fт= Рт*B*R
В режиме всасывания в трубке наблюдается постоянное разрежение относительно внешнего давления, которое обеспечивает всасывание воды на открытом конце трубки вертушки (см.рис.17-Б):
Р= — Рv
Величина прибавки тяги КС ЖРД от коноидально-конического захода на критическое сечение
Удивительно то, что в КС ЖРД даже при очень плавном заходе потока на критическое сечение у потока обнаруживается всего 22-25% прибавки силы тяги струи, вместо ожидаемого 2-х кратного роста тяги, как в случае с несжимаемой жидкостью при истечении из коноидального насадка на отверстие в стенке бака под давлением.
Получается, что в газовой среде куда-то пропадает весьма ощутимая доля энергии разгона потока, не давая получить полное срабатывание внутренней энергии горячих газов в максимальную тягу струи уже на срезе критического сечения КС ЖРД.
К тому же скоростной напор струи газов в критическом сечении даже не создаёт запирающего давления, равного давлению в КС!
Скоростной напор Pv на срезе КС составляет всего 62% от давления Ркс на дне КС.
Это следует из табличных данных (см.рис.11), где сила тяги по импульсу силы.
Следовательно избыточная сила тяги по импульсу силы Fa =124% от Fрv-кр означает, что скоростной напор в критическом сечении находится всего на уровне 124/2= 62% от возможного по имеющемуся давлению Ркс в КС.
Попробуем оценить происходящее в критическом сечении , чтобы создавался нужный скоростной напор от газов, обеспечивая 124% тяги от табличных значений тяги по давлению в КС.
Расчёт № 2
Просчитаем данные по КС и критическому сечению по данным из таблицы в учебнике ( рис.12) и формулам из учебника (рис.11)
qкр=((qкс)^1,15*Ркр/Ркс)^(1/1,15)
Подставляя известное значение давления в КС на уровне Ркс=100атм =10МПа получаем:
qкс=0,031/0,00315=9,84 кг/м3
qкр=0,617*qкс=0,617* 9,84= 6,07 кг/м3
Ркр=0,574*100=57,4атм
Мы получили скорость в критическом сечени.
Так при расчётной по учебнику скорости «звука» в критическом сечении КС:
Vкр-м=Vа* 1,41=1043 * 1,41=1470м/с
Расчёт №3
Несколькими главами ранее мы посчитали предельную скорость газовой струи при полном переводе тепла в кинетическую энергию.
Для керосин-кислородного топлива это составило:
Согласно таблице балансов тяги по ЖРД (см.рис.12) на КС приходится чуть менее 50% (точнее 100%*1,234 / 2,5= 49,36%) от конечной теоретической скорости потока из сопла бесконечного расширения при показателе адиабаты к=1,15. 
При более высокой скорости истечения газов и неизменной тяге в критическом сечении должна уменьшится плотность газов:
Скорость газов из сопла составит Vcоп= 3100м/с (см.рис.3),
А баланс тяги в ЖРД составит
Это вполне попадает в привычные 60-70% в соотношение для распределения тяги между частями ЖРД при работе с подпором атмосферного давления.
G=q*V,
Если бы мы знали реальный параметр G для двигателя, то мы могли бы сделать вывод о том, какая из цифр скоростей Vкр ближе к реальности.
Так мы второй раз выясняем, что для одной и той же КС ЖРД нам нужно использовать разные коэффициенты адиабаты для расчётов разных энергобалансов для одного и того же газа в одном ЖРД. Также требуется уточнить скорость и плотность газов в критическом сечении КС для получения реального распределения импульса тяги между КС и соплом ЖРД.
Аналогичный расчёт необходимо провести для Сопла Лаваля, где нам известен рост скорости .
Происходящее в критическом сечении КС и в сопле Лаваля с точки зрения СТГ
Для расходования остаточного поперечного давления необходимо, чтобы газ совершил работу в поперечном от скорости потока направлении, то есть вдоль элементарного слоя dW.
Но ведь именно поперечное расширение тонких слоёв и создаёт расширяющееся сопло Лаваля в РД!
При этом темп расширения стенок сопла оказывается ниже скорости потока по оси сопла и ниже скорости звук в этом слое газа (угол менее 40 градусов у стенки сопла к оси РД).
Таким образом на стенки сопла действуют силы давления, совершающие работу по отодвиганию стенок сопла. Так стенка сопла отступает по отношению к газу, подобно тому как сверхзвуковое крыло отступает относительно газа (см .часть № 5 данной статьи), теряя на этом внутреннюю энергию слоя газа при адиабатическом расширении с совершением полезной работы.
В этой аэродинамической аналогии получается, что от кромки сопла Лаваля начинает расходится фронт возмущения звуковой волны поперёк потока газа из критического сечения КС в след за отступающей вбок стенкой сопла ЖРД.
При этом и к оси сопла пойдёт фронт возмущения со скоростью звука в газе при данной температуре газов (около Т=2880К), в полной аналогии с поведением газов атмосферы вокруг сверхзвукового крыла.
Этот фронт разрежения газов от кромки критического сечения КС достигнет оси потока газов из КС, образуя конус плотного газа из КС в перевёрнутой усечёной круглой пирамиде разреженного газа в начальной части сопла Лаваля. (см.рис.24-25)
При этом в объёме газа между стенкой сопла Лаваля и конусом плотного газа из КС возникает пространство постоянного низкого давления, в котором частицы газа имеют дополнительную скорость поперёк сопла со скоростью отступания стенки сопла от частиц в потоке струи из КС:
При этом направление разлёта молекул газа в сопле Лаваля со скоростью V4=Vкон-кс будет под углом близким к углу расхождения стенок конической части сопла к оси ЖРД (см.рис.24-25)
После участка правильно конуса сопла начинается часть сопла с плавным снижением угла наклона стенки к оси сопла, где продолжится дальнейшее снижение давления в сопле Лаваля при увеличении поперечного сечения (согласно геометрии сопла) и росте толщин (пропорционально росту осевой скорости) элементарных объёмов dW газа .

Поведение газов в КС на сужении
В реальной КС ЖРД двигателя РД-107 в конической части КС сечение сокращается по диаметру в 2,5 раза от широкой цилиндрической части к самому узкому критическому сечению. Геометрические оценки даны по фотографии с разреза реального РД-107 (см.рис.26)
Тогда можно рассчитать изменение скорости потока при прямолинейном разгоне газов в прямых конических трубках тока, на которые можно разделить весь поток в коническом участке КС.
Изменение в 2,5 раза по диаметру соответствует изменение площадей сечения конуса в 2,5^2=6,25 раза в начале и конце сужения КС.
Также нужно учесть изменение плотности газов при разгоне, которая падает от 9,84 до 2,321кг/м3 (согласно ранее проведённым расчётам), то есть в 9,84/2,321=4,24 раза.
При сохранении постоянного массового расхода G по всем сечениям КС получаем, что скорость в коническом сечении возрастает в отношени.
Таким образом при скорости V3=Vкр=2311 м/с получаем:
V1=2311 / 26,5 = 87м/с
Таким образом поведение газов в КС до критического сечения можно рассматривать как у несжимаемой жидкости с постоянной плотностью, то есть скорость в КС рассчитывается по законам геометрии в соседних сечениях.Скорость жидкого топлива в донной части КС
При плотности жидкого керосина 810кг/м3 и жидкого кислорода 1141кг/м3 средняя плотность жидкой топливной смеси в соотношении 1:2,7 составитПоведение газов в критическом сечении КС ЖРД
Сопряжение конической части КС и конической части начала сопла Лаваля имеет скругление, а потому рассмотреть это участок разгона газов в ЖРД нужно особо внимательно.
Переход между двумя конусными поверхностями КС и сопла Лаваля осуществляется через тороидальную (бублик) поверхность сопряжения (см.рис.24-25).
Тороидальная поверхность- это и есть коноидальный насадок, рассмотренный в парадоксе о вытекании струи жидкости через отверстие в баке.
В коноидальном насадке на коротком участке меняется геометрия слоёв газа от формы сферических слоёв равных скоростей в конической части КС на плоский слой в критическом сечении.
При этом возникает резкое изменение площади сечения с соответствующим ростом скорости потока при постоянном массовом расходе, а форма элементарных объёмов дW становится сложно выгнутой, в зависимости от участка коноидального захода от КС на критическое сечение.
При этом при разгоне совершается значительная трансформация внутренней энерии из тепловой в кинетическую с падением плотности при расширении газа.
В критическом сечении будет наблюдаться резкий рост скорости согласно постоянному массовому расходу по сечениям:
V3 = V1*S1* q1 / (S3*q3)
В данном случае нам будет интереснее величина скорости V2, так как скорость V3=2311м/с при q3=2,321кг/м3 на критическом сечении КС мы уже получили из уравнения фактической тяги КС.
Для двигателя РД-107 (см.фото.рис.26) угол конуса составляет около 32град (оценочно).
Отношение диаметров Д1/Д2= 2,2 (оценочно), соответственно отношение площадей.
Разгон газов в коноидальном заходе КС
Площадь выпуклой поверхности сферического сегмента будет больше площади плоского круга приблизительно в S2/S2-0=1,11 раза.
Общее увеличение скорости на коноидальном заходе:
Таким образом можно смело сказать, что практически весь разгон за счёт изменения плотности .
При этом вся остальная КС может считаться сосудом под постоянным давлением, а газ может считаться почти несжимаемой жидкостью с постоянной плотностью.Зона разрежения в КС на коноидальном заходе
Прибавка 24% от Fкс=РксS3 накладывается на узкую полоску вокруг критического сечения, где уже на относительно высокой скорости в интервале 421..741м/с действует отрывное течение искривлённого потока газов.
По этой модели поведения газов в КС становится понятно, что небольшое смещение термодатчиков по коноидальному заходу может сильно изменить снимаемые показания.
Так температуру сильно меняют значительные тепловые потоки вдоль стенки ЖРД от горячей КС к «холодному» соплу Лаваля.
Ещё сильнее будет аналитическая погрешность при попытке дать оценку методической ошибке измерения по неправильной термодинамической модели процесса.
В связи с мгновенным разгоном молекул в критическом сечении возникает вопрос:
Разгон от скорости Vкс3 до Vкр с одновременным падением СРЕДНЕЙ плотности газа в 4,8 раза осуществляется на очень коротком участке коноидального захода перед критическим сечением. Так в критическом сечении происходит почти мгновенное разуплотнение слоёв потока газа по скорости, при этом поперёк потока плотность молекулярных столбцов молекул газа сохраняется неизменной.
Небольшой участок прямой трубы нужен для полного выравнивания скорости по сечению, чтобы в сопло Лавля поступил уже поток равной скорости.
Искривление формы поверхности равной скорости в критическом сечении идёт от коноидального захода, где скорости потока по сферическим сечениям выравнивались не одновременно, а с отставанием по мере прихода информации от стенок со скоростью звука.
На коротком прямом участке в критическом сечении скорости выравиваются, по мере срабатывания продольного давления в осевое ускорение до Vкр в отставших участках равноскоростных поверхностей.
Так получится «молекулярное сито» с тонкими трубками для прохода молекул строго по очереди.
При этом в теории разгон отдельной молекулы в «моллекулярном сите» возможен вообще на длине одной молекулы, то есть практически мгновенно.
Гигантское ускорение такого разгона объясняется весьма существенным перепадом давления на открытой в вакуум молекулярной трубе, где на бесконечно малой длине элементарного объёма Wмол одной молекулы происходит резкое срабатывание давления в КС равное Ркс=60-250атм до Р=0 в вакууме. При этом при бесконечно малой массе отдельной молекулы такой резкий скачёк давления создаёт гигантское ускорение.
Удельная молекулярная сила разгона одной молекулы составляют:
а=5* 10^15 g= 5000 * 10^12 g
Сильное расширение КС требуется для увеличения времени пребывания холодного топлива в зоне разогретых газообразных продуктов горения.
Длительное время пребывания топлива в КС нужно чтобы впрыснутые в КС холодные жидкие компоненты топлива успели испариться, перемешаться и вступить в реакцию с выделением тепла.
Если КС будет выполнена в виде узкой длинной трубы постоянного диаметра, то такой длительный испарительно-нагревательный процесс будет невозможен, так как резкое изменение плотности среды при испарении отдалит зону горячих расширяющихся газов от холодного начала КС.
В результате в сильно удлиненной КС тепло из зоны горения не сможет попасть назад в сильно отдалившуюся зону испарения.
В итоге произойдёт срыв пламени, горение в КС остановится совсем, КС захлебнётся не газифицырованным холодным жидким топливом, и ЖРД потухнет.
Кстати на основании данного тезиса можно предложить инновационную форму КС в виде полушария и ли почти полного шара, отличную от привычных цилиндрических КС с конусным переходом на критическое сечение.Инновационная форма КС.
В такой полусферической КС будет крайне вольготно располагать форсунки впрыска топлива по большой площади сферического дна КС. При этом обеспечивается равномерный разгон по идеально «конусным трубкам тока» продуктов горения от форсунок до критического сечения КС по центру полусферы.
Подпор плоской стенки полусферической КС вполне возможно осуществлять за счёт охлаждаемой полости с топливом-охладителем, находящимся за стенкой КС под давлением впрыска, равным давлению в КС. (см.рис.27)
Так в ЖРД малой мощности, где относительная длина КС в составе ЖРД очень велика (см.рис.26.), использование более компактной шаровой формы КС может сильно сократить длину ЖРД, а большая площадь полусферического форсуночного дна КС позволит удобнее подводить большое количество трубопроводов к отдельным форсункам.
Так КС с длинной цилиндрической частью с соотношением сторон 3*Д=L можно заменить на полусферическую КС с диаметром 2Д, или на полную сферу диаметром 1,7Д.
При этом для КС в виде полной сферы конус сужения с коноидальным заходом будет входить глубоко в центр шаровой КС.
Поток излучения и конвективные горячие струи из зоны горения в центре сферы поступают к периферии КС и расходуются на испарение жидких компонентов топлива.
Керосин разбрызгивается непосредственно по поверхности сферы, а кислород подаётся над кипящим и испаряющимся керосином, интенсивно смешиваясь с парами керосина до нужных концентраций.
Горение же начинается уже ближе к центру сферы, достигая максимальной температуры уже перед входом в коноидальный заход по центру сферы.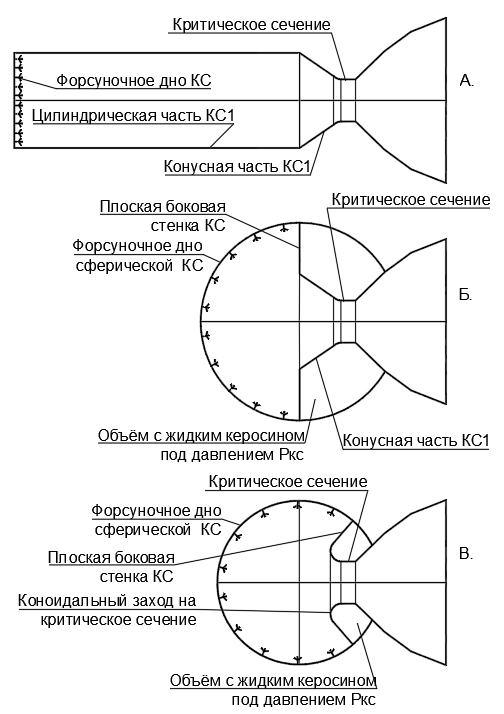
А- цилиндрическая КС с соотношением Длина/диаметр как 3:1.;
Б- Полусферическая КС;
В- сферическая КС с глубоким входом коноидального захода внутрь сферы КС.Форма захода на критическое сечение КС
В сопряжении конуса КС с цилиндром критического сечения КС возможен как плавный переход со скруглением относительного большого радиуса (как у коноидального захода), так и резкий излом (см.рис.28)
То есть коноидальный заход выгоднее резкого излома разгонных поверхностей в КС.
А вот замена плавного перехода на резкий излом в сопряжении критического сечения КС и сопла не повлияет на течении газов в КС, но лишь создаст более резкий газодинамический фронт поперечной волны давления в потоке газов уже в начале сопла Лаваля в конусе постоянного давления.
Такие резкие ломанные переходы от КС к расширяющемуся соплу являются часто встречающимся решением, упрощающим конструкцию малых РД.
При переходе от прямолинейного течения конусной части КС на коноидальную поверхность об изменении направления потока узнает не всё сечение струи сразу, а только крайние к стенке КС слои газа. При этом распространение информации по сечению от стенки к оси ЖРД пойдёт со скоростью не выше скорости «звука» для данного сечения при данной температуре. Учитывая относительно небольшую ещё скорость на сечении S2 при высокой температуре, то выравнивание скоростей по сечению создаст не очень сильное запаздывание на участке начала коноидального захода. Так в итоге в критическом сечении (любой формы) формируется поток газов с почти постоянной скоростью по критическому сечению КС.
Этот сплошной поток газов при выходящий в объём сопла Лаваля превращается в конус.
Конус формируется в зоне резкого расширения сечения сопла, при постепенном растекании потока в радиальном направлении. При этом скорость отступания фронта перепада давления на поверхности этого конуса (образующей конуса) к оси сопла равна скорости звука в V3a.
Наклон образующей конуса определяется векторным отношением осевой скорости потока V3 в критическом сечении к скорости звука в критическом сечении V3а.
Так как по нашим расчётам скорость газов V3кр в критическом сечении больше скорости звука V3а приблизительно в 2 раза, то конус плотного потока из КС в сопле будет иметь вид острого конуса.
Если же тороидального скругления в сопряжении конусов нет, а конусы граничат по излому образующих (что допустимо), то скачёк скорости в 1,5 раз на сопряжении КС и сопла происходить практически также, но без предварительногь выравнивания потока по критическому сечению и с некоторыми резкими возмущениями при отрыве струи на изломе.
При этом критическое сечение необходимо считать с корректировкой на сегментно-сферическую форму с коэффициентом для выпуклой поверхности.
Тут мы опять вспоминаем про «парадокс истечения жидкости из отверстия» и понимаем, что коноидальное сопряжение конусов лишь повторяет естественное течение струй потока, а не формирует его.Разгон газов в сопле Лаваля
Но если у массы газа уже имеется максимальная возможная продольная скорость по оси РД в критическом сечении КС, то как её увеличивать в сопле Лаваля?
Здесь можно предположить, что работа слоя при расширении как раз и расходуется на ускорение газа.
Для объяснения создания ускорения молекул газа в сопле Лаваля нам нужно оперировать не плоскими, но арочными слоями, имеющую проекцию на ось РД от касательной к тонкому слою(см.рис.29).
Как выясняется, наличие таких сферических слоёв подразумевается при построении линий тока в КС и в сопле.
В сужении КС линии тока сходятся в пучёк в критическом сечении, а потом расширяются веером в сопле за критическим сечением.
Линии тока- это по сути траектория движения молекул газа в РД.
Направление движения молекул по этим линиям определяет равнодействующая сила на отдельной молекуле или направление градиента давления.
То есть в направлении перпендикулярном к линиям градиента давления изменение давления будет равно нулю, а направление постоянного давления- это линия изобары (линия постоянного давления).
Рассмотрим простейший вариант формы сужения и расширения по коническим поверхностям с линейными образующими.
Линии изобар в таком расходящемся пучке линий тока создают сферические поверхности, перпендикулярные линиям градиентов давления.
Молекулы на этой сферической поверхности испытывают одинаковое максимальное ускорение по направлению движения по линии градиента и нулевое ускорение по изобаре вдоль своего сферического слоя.(см.Рис.25)
То есть сферический слой по изобаре в РД и есть та самая арка из молекул под давлением, существование которой мы предположили ранее!!!
Сферические арочные поверхности изобар могут не совпадать с перпендикулярными к линиям тока поверхностями, но только если линии тока изогнуты, а не линейны.
Так при круговом движении потока возникают центростремительные ускорения, перпендикулярные к вектору скорости. При этом центростремительные силы, направленные по радиусу кривизны, не совершают работы.
Так в предельном случае в изогнутом потоке с постоянной скоростью изобары не являются перпендикулярами к направлению потока, а совпадают с линиями тока. Примером таких статичных изобар по линиям тока являются вращающийся чай в стакане (рис.17-18) или давление поперёк сечения на изгибе водопроводной трубы (см. главу про разбор «вертушки Феймана»).
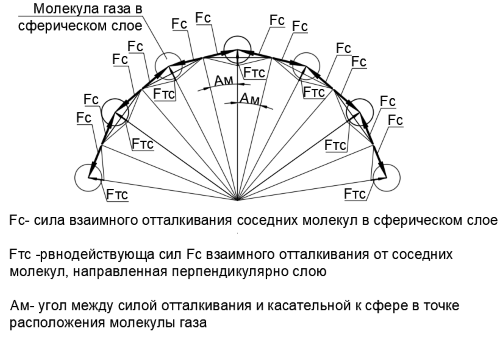

Рис.33. Схема сил отталкивания в сферическом слое, создающие разгонную силу на молекулах перпендикулярно слою.Вид ссверху на шестигранную ячейку молекул в единичном сферическом изобарном слое в ЖРД.(Вид на силы в плоскости слоя в плане)
Именно так энергия поперечного давления газов трансформируется в дополнительный продольный разгон этих газов в сопле Лаваля.Торможение потоков в КС ЖРД
При разгоне газов в зоне коноидального захода кривизна арочных слоёв резко падает, переставая тормозить осевое ускорение слоёв. При этом на критическое сечение КС, где скорости быстро приближаются к скорости звука, молекулы перестают успевать выравнивать свой порядок до равномерного расположения в пространстве.
При заходе на коноидальную поверхность сужения начинает накапливаться неоднородность плотности молекул в рядах вдоль и поперёк скорости потока. Неоднородность рядов молекул достигает максимума при резком расширении вперёд в прямом (цилиндрическом) участке критического сечения КС. В этот момент внутренняя энергия по направлению вдоль оси РД срабатывается почти полностью в кинетическую энергию, а поперчное давление на паралельных стенках трубы работу совершить не может.
Эта нерастраченная энергия поперечного давления в КС потом обращается в продольный разгон в сопле Лавля при расширении таких же арочных слоёв, но с выпуклостью уже наружу.
Что-то в работе ЖРД мы смогли посчитать по известным нам законам газовой динамики и свести всё к вполне вменяемому энергетическому балансу по КС от дна до критического сечения.
Осталось только объяснить поддержание избыточного давления в КС непосредственно перед дырой наружу.
Что мешает струе газов разогнаться в пустом отверстии до запирающего давления Рv=Ркс, а не останавливаться на величине 62% от Ркс?
Ведь по бытовой логике давление должно быть сработано почти до нуля в отверстии при разгоне до звуковой скорости в критическом сечении, но что-то этому объективно мешает.
Бытовая логика не учитывает реальное взаимодействие по отдельным направлениям между отдельными молекулами газа по СТГ.
Из этого следует, что привычные равновесные представления для спокойных газов не применимы для быстротекущих процессов с большой неравномерностью динамики по отдельным осям.
То есть в критическом сечении КС существует два разных давления :
В любом случае остаётся вопросы :
Откорректированный график должен быть менее гладким, имея резкие переходы на коноидальном заходе в КС, резкий скачёк на критическом сечении и излом при переходе в сопло Лаваля (см.рис.34). Причём такие резкие трансформации в зоне критического сечения КС будут у графиков всех параметров (V, T , P).
Конусная часть сопла заканчиваяется при срабатывании центрального конуса газов из КС. На графиках появились горизонтальные полки в зоне постоянного разрежения при срабатывании конуса газов из КС.
Интересно, что после окончания конусного участка КС начинается снижение угла наклона стенок к оси, что означает снижение темпа расширения газов в связи с падением скорости «звука» в слое газа из-за снижения его температур при расширении.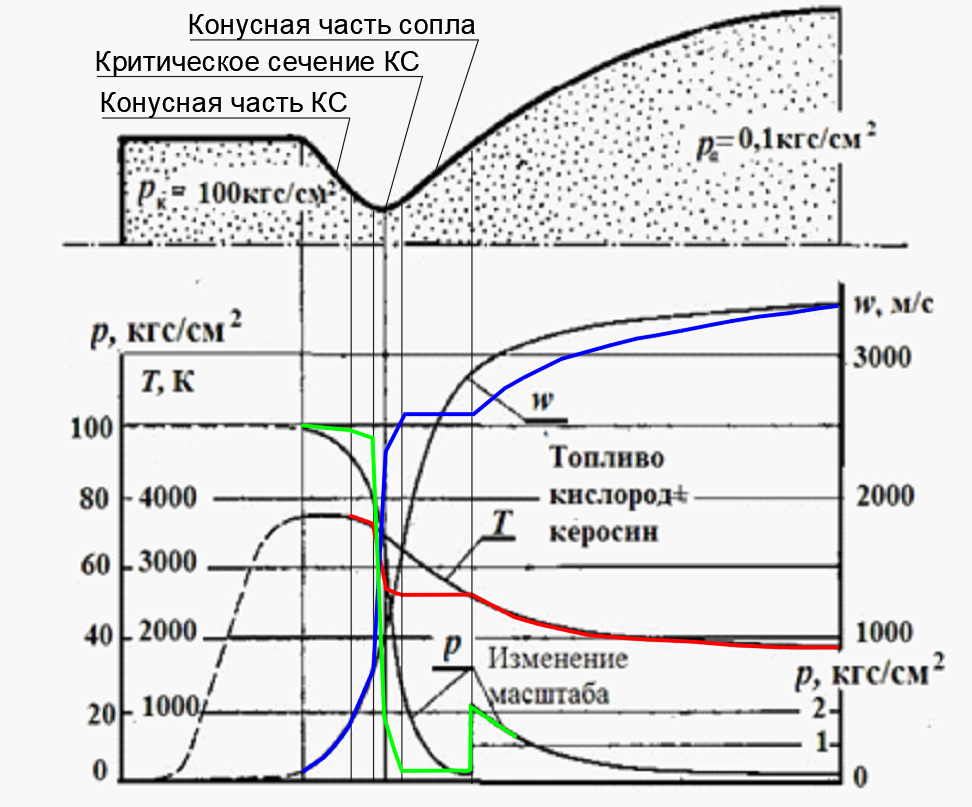
Такое последовательное трёхмерное расширение газов по разным направлением как раз реализовано в типовом ЖРД.
Так в ЖРД сначала происходит расширение по оси КС вдоль скорости, с выработкой продольной части сил упругости поля отталкивания молекул.
Процесс продольного расширения газов за счёт внутренней энергии полностью завершается в критическом сечении КС при достижении «локальной скорости звука» .
Термин «локальная скорости звука» взят в кавычки, так как он является простой натяжкой расчётной формулы на реально полученное значение скорости потока в критическом сечении КС без нормального физичного обоснования данного явления.
Затем в расширяющейся части сопла Лаваля происходит плоское расширение слоёв в поперечных направлениях к скорости (вдоль сферического слоя молекул).
Схема такого неравновесного послойного расширения газов в отдельных частях ЖРД представлена на схеме (см. рис.30-33.)
Расстояние между молекул в сферическом слое равно
Угол Ам в сферическом слое крайне мал, но при этом масса молекулы газа так же крайне мала.
а=3*R*T/(Rсл*Mr)
Кривизна слоя задаётся формой расширения в сопле Лавля.
Вариант с температурой легче в расчёте, так как её можно мерять непосредственно на поверхности сопла, в точке с фиксированным радиусом кривизны слоя, который нужно выстраивать перпендикулярно к поверхности сопла в данной точке замера.
С замерами Температуры и давления в зоне критического сечения КС ситуация сильно сложнее, так как из-за резкого изменения направления потоков газов давления и температуры у поверхности КС сильно отличаются от тех же параметров внутри потока газов ближе к оси КС этого же сечения.
Т=3500К
Mr=0,031 кг/м3 (СО2+Н2О)
Тогда ускорение равно:
Правда заметное тормозящее влияние арочные слои будут оказывать только в коноидальном заходе на критическое сечение, где скорость потока будет приближаться к звуковой и выравнивание плотности газа по объёму уже не будет происходить.
Малое давление Рторм может существовать при больших избыточных силах Fc (давление поперёк потока), если сферический слой в критическом сечении КС имеет крайне малую кривизну ( Rсл уходит в бесконечность).
В конце коноидального захода на участке прямой трубы в критическом сечении прогиб арок молекулярных слоёв становится нулевым и остаточное давление газов вдоль оси потока мгновенно срабатывается в ускорение газов от Vкс-s3=741м/с до Vкр=2311м/с., мгновенно охлаждая газ на 870К
Это разгонный скачёк обеспечивает недостающее давление в критическом сечении. Перепад разгонного давления создаётся буквально на толщине нескольких молекулярных слоёв, что делает газодинамику в критическом сечении столь плохо наблюдаемой инструментальными средствами, особенно если анализ результатов измерений ведётся в рамках КТГ.
Работа газов поперёк сопла на убегающей от слоя стенке сопла- это и есть полезная работа сопла ЖРД в полёте.
Максимальный КПД ЖРД как движителя ракеты возникает при скорости ракеты равной скорости газов на срезе сопла.
То есть в этом режиме вылетающие из сопла газы имею нулевую кинетическую энергию при нулевой скорости относительно окружаещего воздуха верхних слоёв атмосферы, где ракета достигает скорости 3000м/с.
Получается, что летящая в атмосфере на скорости 3000м/с ракета оставляет за собой неподвижный столб горячих газов, который даже не расширяется при равенстве давлений на срезе сопла с атмосферой в высотном ЖРД, или незначительно расширяется, если сопло было на первой ступени РН с расчётом на высокое атмосферное давление на уровне моря с достижением скорости 3000м/с в высоких и менее плотных слоях атмосферы.
После остывания этот столб газов за ракетой ещё и сильно сжимается.Форма сопла Лаваля в ЖРД
Сопло можно разворачивать на большие углы, в том числе до 180 градусов.
Примером вырожденного сопла может послужить «развёрнутое» или «плоское сопло».
Вспомним, что в вакууме газ расширяется из точки в сферу, увеличивая радиус почти в бесконечность.
Зная озвученные ранее построения об арочных сферических слоях в РД можем построить почти идеальны по форме реактивный двигатель.
Таким «идеально-теоретическим» соплом РД будет плоскость. В одном полупространстве от этого плоского сопла начнёт расширятся облако горячего газа в виде идеального полушария, оказывая строго перпендикулярное давление на плоскость, там где сферический слой газа будет касаться плоскости «сопла». (см.рис.35)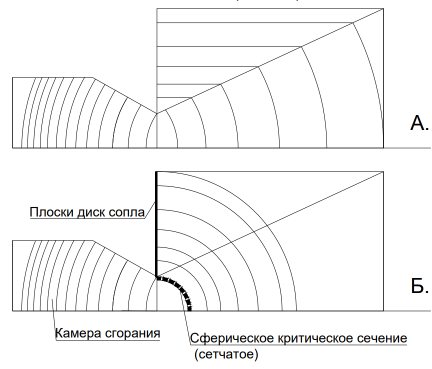
КПД плоского сопла будет однозначно ниже, чем у направленного сопла Лаваля.
Выражаться это сравнительное КПД плоского и направленного сопел будет достаточно простым соотношением: площади сечения шаровой поверхности (площадь круга) к площади полусферы.
Если вспомнить, что площадь сферы: Sсф = 4*R^2 * 3,14
Это значит, что на создание одинаковой тяги потребуется расхода в 2 раза большего количества топлива при в 2 раза меньшем КПД.
Употребление слова «Почти» связано с неустранимой сферичностью потока на срезе сопла (незначительная выпуклость с радиусом сильно больше размера сопла по длине у криволинейных сопел), так что маленькое ухудшения превосходства КПД от 2-х кратности будет всегда.
Кстати, это двукратное усиление КПД при направленом сопле используют при подрыве взрывчатого вещества (далее ВВ) во взрывчатых боеприпасах некоторых типов.
Так обычно ВВ в виде цилиндра внутри снаряда взрывают рядом с бронёй танка и получают локальное сферическое образование ударной волны. В специальных же боеприпасах ВВ взрывают не рядом с бронёй танка или укрепления, а позволяют пластичному ВВ расплющится о поверхность подрываемого объекта, а потом уже этот плоский «блин» взрывают донным взрывателем снаряда.
При таком плоском подрыве одинаковое количество взрывчатки даёт в два раза большее ударное воздействие на препятствие, чем при подрыве ВВ в виде компактного цилиндра на небольшом удалении от брони.
Похожим образом делают проломы в стенах при штурмовых операциях, прикладывая плоски лист динамита (плоский ящик с динамитом) к стене.
Вернёмся к плоскому соплу.
При свободном расширении газов сразу во всех направлениях равномерно (сферическое расширение), вся исходная тепловая энергия молекул горячих газов будет полностью сохраняться в кинетической составляющей разлетающихся молекул газа, которую нечем будет затормозить при отсутствии стенок сосуда в бескрайнем космосе. Так получаются совершенно холодные, но очень быстрые атомы газа в вакууме.
Кстати, шаровой разлёт газа в вакууме с непрерывным приращением скорости отдельных молекул газа- это ещё одна демонстрация недостоверности КТГ.
Так в сильно разреженном шаровом слое молекулы никак не могут друг с другом сталкиваться для взаимного разгона, так как они уже летят в разные стороны на больших расстояниях друг от друга. Но при этом в шаровом слое молекулы продолжают друг от друга отталкиваться продолжая разгон при невероятно высоких степенях расширения (разрежения).
Таким образом, повышение давления уменьшает габариты проточной части КС в ЖРД. Правда радужность картины снижается из- за повышения толщин стенок КС на более высокое давление. Также утяжеляется и становится более мощным турбонасос для пропихивания того же расхода G несжимаемого жидкого топлива в КС с более высоким давлением.
Давление в КС первых баллистических ракетах начиналось с 60 атм ( как в дизельных двигателях) . Теперь давление достигло 250атм (РД-170).
Так по нашему расчёту в критическом сечение поперечное давление составляет 18атм.
Для срабатывания избыточного давления 18 атм до уровня наружного атмосферного давления требуется сопло достаточно небольшого расширения от диаметра критического сечения КС.
У двигателя РД-107 (Ркс=60атм) степень расширения составляла всего 18,86. То есть диаметр увеличивался от критического сечения КС до среза сопла всего в 4,34 раза (см. фотото.рис.26)
Тогда для 250атм (РД-170) потребовалась большая кратность расширения в сопле, достигнув величины 36,8 раза, или рост диаметра сопла в 6,07 раз (рис.36).
Подняв давление в 4 раза от 60атм до 250 атм можно снять в 4 раза большую тягу с КС и Сопла практически неизменного размера.
Интересно заметить, что повышение давления в КС приводит к уменьшению длины КС, так как одинаковое время протекания процесса испарения и горения топлива при большей плотности газов в КС обеспечивается на более коротком пути от форсунок до критического сечения КС (см рис.26,36). Такое сокращение длины КС позитивно сказывается на общем снижении веса ЖРД.
Выше 250 атм поднимать давление уже не выгодно, так как начинается столь значительный рост массы двигателя для обеспечения прочности стенок, что прирост массы уже не компенсируется ростом импульса тяги ЖРД (РД-107 импульс в вакууме 313с при Р=60атм, РД-171 импульс в вакууме 337 с при Р=250атм)
Это можно считать пределом возможности геометрического увеличения размера КС ЖРД, что связано с достижением критически большого размера отверстия критического сечения КС.
Так РД-107 (тяга 102тс) отличается по тяге от РД-170 (тяга 806тс) в 8 раз, но из-за большего в 4 раза давления в КС (60атм против 250 атм) критическое сечение КС двигателей отличается всего в 2 раза, а диаметры всего в 1,4 раза (корень из 2-х).
При этом в росте в линейного размера критического сечения КС ограничивающую роль играют роль два фактора :
-становится слишком малой кривизна запирающего слоя на коноидальном заходе к критическом сечению (большой радиус кривизны= малое давление запирания), в результате КС превращается в прямую трубу с низким давлением и с неполным сгоранием топлива.;
-слишком большой радиус отверстия критического сечения создаёт условия, что возникает центральный участок критического сечения, до которого информация об искривлении стенок КС не успевает долетать поперёк потока газов. Таким образом создаётся неравномерность скорости по критическому сечению КС, которая не успевает выровнятся до входа в сопло, создавая сильную пульсацию давления в КС, тем самым не давая поднять давление в КС. Так из КС проскакивают потоки плотных холодных низкоскоростных газов несгоревшего топлива.
Это наводит на размышления о работоспобности двигателя F-1 c РН Сатурн-5, участвовавшего в лунной программе США.
Так КС F-1 имеет столь малое заужение в критическом сечении (см рис.37-38), что не позволяет наедятся на достижение заявляемого давления 70 атм (сравните с сечением РД-107 с чуть меньшим давлением Ркс=60атм). Скорее такой ЖРД будет работать как довольно мощная факельная горелка, фонтанирующая плохо сгоревшим топливом, что видно на кадрах его испытания на стенде (см.рис.39).
Такого явления у советского РД-107 не наблюдается (см.фото.рис.40), так пламя из сопла на столько прозрачное, что на фото сквозь струю газов из сопла видна дальняя кромка этого сопла. При этом слой холодного газа из несгоревшего керосина-охладителя тоже есть, именно это топливо на периферии струи вспыхивает ярким непрозрачным пламенем уже далеко после вылета за края сопла.
Хорошо известны весьма скептические слова конструктора советских ЖРД Валентина Глушко, когда он узнал про разработку в США однокамерного ЖРД на 800тс тяги: «Пусть попробуют… упрутся в ту же стену, в которую упёрлись мы».
Самый мощный на текущий момент ЖРД с тягой 806тс является именно четырёхкамерный ЖРД Глушко РД-107, а у него тяга одной КС составляла всего 200тс, которые и можно считать геометрическим пределом.
При этом на малых ЖРД с критическим сечением небольшого диаметра легко достигаются высокие давления в КС, да и работают такие мелкие ЖРД весьма стабильно.
С такой стабильной работой малых КС связана тенденция, что пытаются создавать поликамерные КС, работающие на одно сопло. Отказ одной из камер в поликамерной КС не должен вызвать срыв пламени в других камерах, а ЖРД в целом продолжит работу с небольшой потерей мощности.
Именно к таким поликамерным односопловым ЖРД относятся ЖРД с центральным телом: сопло с центральным диском, сопло с центральным круглым телом (штыревые) или с плоским телом (плоское сопло) (См .рис.21)



Теория устройства ракетных двигателей: учебное пособие /
А.В. Яскин; Алт. гос. техн. ун-т, БТИ. Бийск: Изд-во Алт. гос.
техн. ун-та, 2013 262 с.


