
Рожденный ползать — летать не может. Эту фразу можно применять как в метафорическом смысле, так и в буквальном, ибо существа без крыльев (или подобных по функционалу частей тела) действительно не способны покорять небеса. По крайней мере, большинство из них. Правило не было бы правилом, если бы не было исключений. В аспекте бескрылых полетов исключения также имеются — украшенные древесные змеи (Chrysopelea). Представители этого рода змей способны парить — крайне полезный навык учитывая, что живут они в кронах деревьев высоко над землей. Ученые из Политехнического университета Виргинии (США) решили рассмотреть полет змеи с точки зрения кинематики. Какие анатомические особенности позволяют змеям летать (контролировано падать, если точнее), что происходит во время полета с точки зрения кинематики, и как данное исследование может помочь в робототехнике? Ответы на эти вопросы ждут нас в докладе ученых. Поехали.
Основа исследования
Украшенные древесные змеи это род змей из семейства ужеобразных, обитающие в Южной и Юго-Восточной Азии. Представители этого рода не могут похвастаться большими габаритами (длина тела всего лишь от 0.6 до 1.5 м) и смертоносным ядом. Хотя добыча, на которую они охотятся в дневное время, не согласилась бы с последним. Учитывая место обитания (кроны деревьев), у данных змей крайне мало врагов, потому особой нужды в сильном яде у них нет. К тому же у них есть куда более эффектная тактика — они умеют планировать.

Летающие змеи, как их еще называют в народе, ползают по деревьям, используя жесткие чешуйки вдоль живота, позволяющие им двигаться вертикально. Если змея желает перебраться с одного дерева на другое, она в первую очередь подползает к краю ветки, затем складывает тело в форму латинской буквы «J», чтобы прицелиться (определить желаемый угол «взлета» и место посадки). Сказав «поехали», змея толкает свое тело вперед и вверх, втягивая живот и выпячивая ребра (так ее тело становится более плоским и слегка вогнутым). Во время планирования змея постоянно совершает серпантиновидные движения телом из стороны в сторону, что позволяет ей контролировать полет и мягко приземлиться.
Вид сбоку на длинное планирование летающей змеи Chrysopelea paradisi.
Дополнительным плюсом столь необычного для змей метода передвижения является внушительная экономия энергии, ведь перелет гораздо быстрее (и безопаснее) медленного переползания с дерева на дерево по земле. Из одно лишь этого короткого описания понятно, что в механике полета змеи имеется множество важных элементов; угол взлета, форма тела во время взлета и полета, движения телом в полете и т.д.
Самым ярким, особенно для наблюдателей, аспектом полета змеи является волнистое движение тела. Эта техника применяется множеством существ на планете для перемещения по земле и по воде. Далеко ходить не надо, ибо сами змеи ею прекрасно пользуются. Ученые отмечают, что волнистое движение по суше и воде изучено довольно хорошо, а вот подобные пируэты в воздухе пока остаются загадкой.
У змей Chrysopelea волнистость характеризуется S-образной формой тела, низкой частотой волнистости (1–2 Гц) и уплощенным аэродинамическим поперечным сечением тела.
Изображение №1
По сути воздушная волнистость непрерывно перестраивает тело змеи, превращая его по форме в крыло (1е). Ранее проведенные исследования показали, что летающие змеи всегда исполняют волнистые движения в полете. Однако остается неясным, является ли волнистость основной частью успешного полета или это просто привычка, т.е. поведенческий аспект перемещения по суше, перекочевавший в полет без каких-либо намерений.
Если учитывать волнистость на суше и воде, то можно предположить, что и в воздухе она генерирует тягу. На твердых средах волнообразное движение происходит благодаря распределенным контактным силам над вентральными и латеральными областями тела, а в воде смещение или всасывание жидкости вдоль тела вызывает движение вперед. В обоих случаях чистая движущая сила действует преимущественно в плоскости волнистости. Модуляция тела вне плоскости (в вертикальном направлении) может использоваться для вторичных целей, таких как уменьшение сопротивления или увеличение нормальной силы.
Но вот для летающих змей успешное планирование требует генерации аэродинамических сил, необходимых для компенсации веса животного. Силы подъема и сопротивления создаются воздухом, протекающим по сплющенному телу, когда оно ускоряется вниз под действием силы тяжести, при этом возвратно-поступательное движение, вызываемое мышечными сокращениями, вероятно, не увеличивает генерацию силы.
Вид спереди на взлет и уплощение летающей змеи Chrysopelea paradisi.
Результирующие аэродинамические силы должны действовать вне плоскости волнистости, а сама волнистость должна постоянно менять распределение сил на тело змеи. Стоит также учесть, что летающие змеи могут «волноваться» не только горизонтально, но вертикально. Значит, что в модели полета змеи присутствуют как элементы тангажа*, так и элементы крена*.
Тангаж* — угловое движение относительно горизонтальной поперечной оси инерции.
Крен* — угловое движение относительно его продольной оси.
В данном исследовании ученые решили детально рассмотреть роль волнистости в полете змеи. Используя записи высокоскоростной съемки полета змеи, ученые смогли количественно измерить воздушную волнистость. Полученные данные позволили создать точную трехмерную модель полета змеи.
Результаты исследования
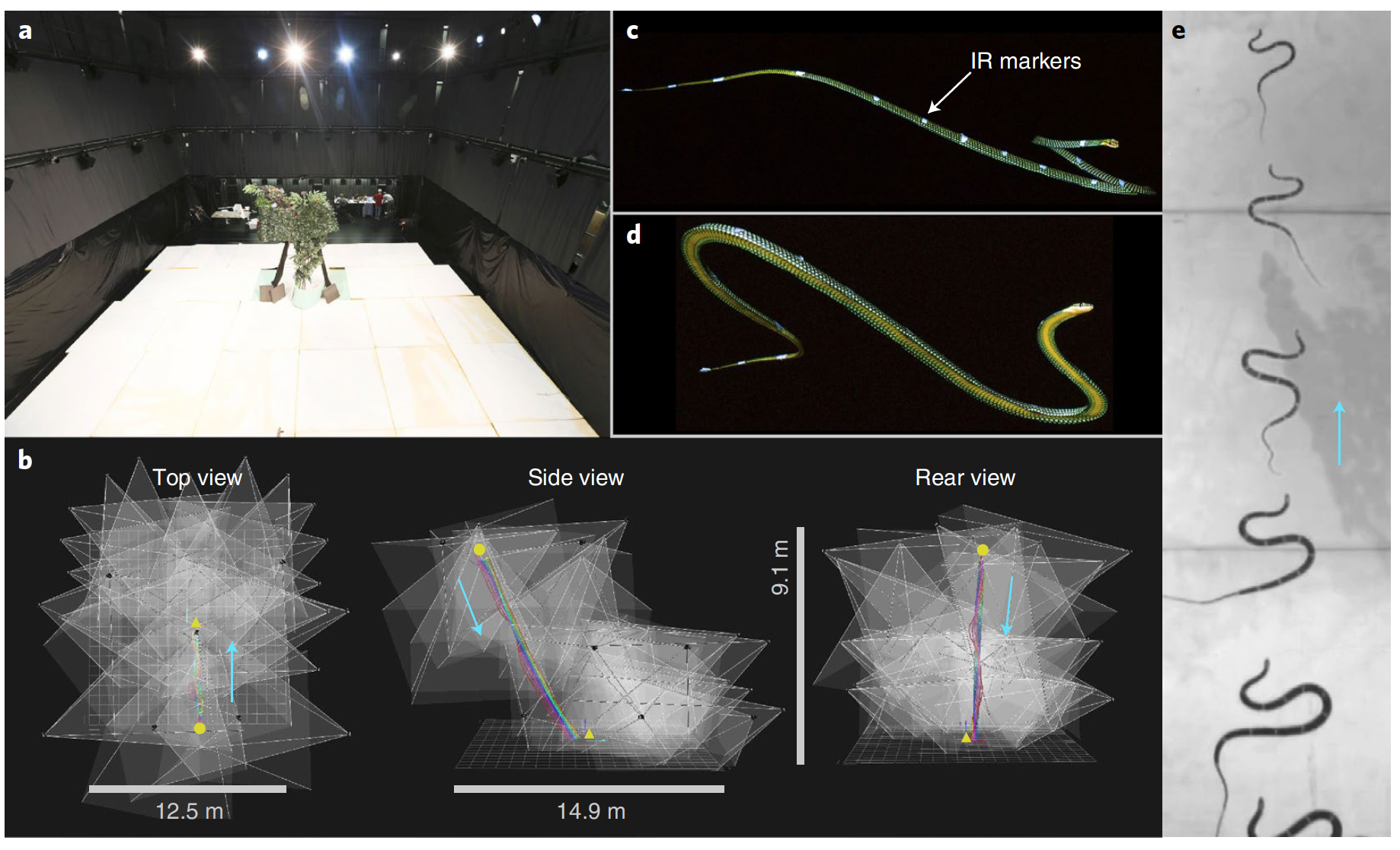
Воздушная волнистость состоит из связки волн горизонтального и вертикального изгиба. Вдоль тела змей (7 особей), участвовавших в съемке полета (высока взлетной площадки 8.3 м), были размещены 11-17 маркеров. Оценка изменения положения этих маркеров позволяет точно определить структуру волнистости во время полета.
Вид сверху на тестовое планирование летающей змеи Chrysopelea paradisi.
Инфракрасные маркеры, полученные во время планирования летающей змеи Chrysopelea paradisi.
Проведя 36 практических наблюдений, ученые создали трехмерную модель тела змеи ( r ).
Разработка 3D-модели летающей змеи Chrysopelea paradisi по данным захвата движения.
Используя касательный вектор (t̂ = ∂r/∂s), удалось разложить волнистость на две угловые волны изгиба, которые движутся вдоль тела.
Горизонтальные и вертикальные волны задаются следующими формулами:
θ̅(s, t) = -tan-1 t̂ x / t̂ y
и
ψ̅(s, t) = sin-1 t̂ z
где θ̅(s, t) и ψ̅(s, t) — локальные углы, которые тело образует относительно горизонтального и вертикального направлений, как функции длины дуги s и времени t.
Данные показывают, что летающие змеи используют две волны: горизонтальную волну с большой амплитудой и вертикальную волну с меньшей амплитудой, обе из которых последовательно проходят вниз по телу от головы к хвосту (изображение №2).

Изображение №2
Эти волны формируются после начального переходного процесса, когда змея прыгает в относительно прямой позе и затем формирует характерную S-образную позу для планирования.
Существует четыре особенности воздушной волнистости, связывающей вертикальную волну с горизонтальной (2а). Во-первых, вертикальная волна имеет пространственные и временные частоты, в два раза превышающие частоты горизонтальной волны. Это указывает на то, что у тела в два раза больше вертикальных изгибов, чем боковых (2а, 2е). Во-вторых, U-изгибы на теле летающей змеи можно идентифицировать как нулевое пересечение на графике угла изгиба (2b). В-третьих, эти пересечения являются максимумами вертикальной волны, указывая на то, что горизонтальные и вертикальные волны сдвинуты по фазе на 90°. В-четвертых, максимальный изгиб вне плоскости происходит на U-изгибах и примерно на середине прямых сегментов. На U-изгибах поперечное сечение «крыла» змеи сворачивается из-за движения тела вне плоскости (1c, 1d).
Форма бегущих волн изменяется со временем, поскольку змея ускоряется и производит аэродинамические силы, однако некоторые особенности все же остаются общими. Горизонтальная волна представляет собой синусоиду с плоским верхом, амплитуда которой (80-120°) зависит от количества пространственных периодов, причем меньшее количество периодов приводит к более высоким горизонтальным углам изгиба. Вертикальная волна представляет собой узкопиковую синусоиду с широкими впадинами с амплитудами в диапазоне от 20° до 45°.
Количественная оценка пространственных и временных характеристик волн показала, что змеи используют горизонтальные волны с 1–1.5 пространственными периодами и частотой волнистости 1-1.7 Гц и вертикальные волны с 2–3 пространственными периодами и частотой волнистости 2–3.4 Гц.
В воздушной волнистости есть дополнительный компонент, который ученые назвали «дорсо-вентральным изгибом», представляющий движение вверх и вниз задней части тела относительно головы. Угол наклона этого изгиба составил от -20° до 30°. Дорсо-вентральной изгиб всегда присутствовал в наблюдаемых полетах, но не имел значимой связи с количеством пространственных периодов.
Чтобы точно определить степень влияния связи горизонтальных и вертикальных волн, а также влияние дорсо-вентрального изгиба на динамику полета, ученые создали анатомически точную модель змеи в полете. Контроль над моделью позволяет, по словам ученых, систематически проверять, как компоненты волнистости (амплитуда горизонтальной волны, количество пространственных периодов и частота волнистости) влияют на краткосрочную и долгосрочную динамику планирования.
Горизонтальная волна моделируется как синусоида с плоской вершиной большой амплитуды, а вертикальная волна — как синусоида небольшой амплитуды:
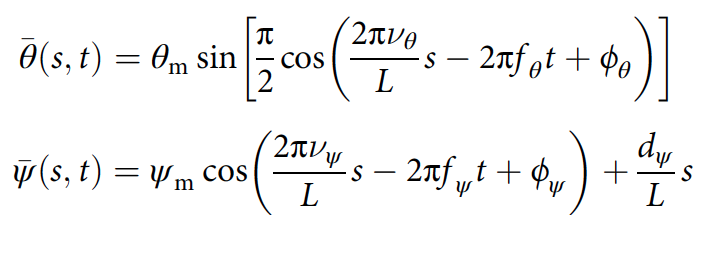
где θm and ψm — максимальные горизонтальные и вертикальные углы изгиба; ν — число пространственных периодов; f — частота волнистости; ϕ — фазовый сдвиг; dψ — дорсовентральный угол изгиба; L — длина тела (2f, 2g).
Горизонтальные и вертикальные волны связаны в кинематических данных (2е): νψ = 2νθ, fψ = 2fθ и ϕψ = 2(ϕθ — π/2). Это сильно упрощает модель до 5 переменных, определяющих форму тела: θm, ψm, νθ, fθ и dψ.
Положение r = [x, y, z] тела относительно центра масс рассчитывается следующим образом: ∂sx = cosψ̅sinθ̅, ∂sy = -cosψ̅cosθ̅ и ∂sz = sinψ̅.
Положение центра масс R0 и ориентация тела (углы рыскания*, тангажа и крена) определяются путем интегрирования уравнений поступательных и вращательных движения.
Рыскание* — угловые движения относительно вертикальной оси.
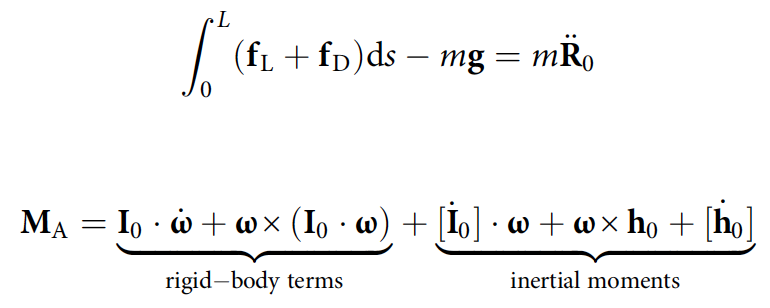
где fL и fD — бесконечно малые силы подъема и сопротивления; MA — аэродинамический момент; m — масса змеи.
Для подтверждения того, что математическая модель дает физически реалистичные результаты, ученые смоделировали полеты, используя параметры, полученные во время фактических наблюдений планирования реальных змей (сравнение моделирования и наблюдений показано на изображении ниже).

Изображение №3
Судя по сравнению, модель работает, однако имеет некоторые незначительные неточности, которые требуют устранения в будущем.
Для проверки влияния волнистости на характеристики планирования было проведено два моделирования: с fθ = 0 Гц (без волнистости) и fθ = 1.2 Гц (средняя частота волнистости у змей). В обоих вариантах варьировались νθ и θm (4а).

Изображение №4
Кинематические данные формы тела змеи в модели позволили получить 121 форму с 1 ≤ νθ ≤ 1.5 объемными волнами и амплитудами горизонтальных волн в диапазоне 90° ≤ θm ≤ 119°. Далее из этого массива были выделены наблюдаемые формы тела (средняя часть графика, отделенная по диагонали; 4b). Часть графика, что ниже выделенной, содержит «открытые» (напоминающие букву S) формы тела, а верхняя — «закрытые» (напоминающие знак бесконечности).
Амплитуда вертикальной волны и дорсовентральный угол поддерживались на постоянном уровне: 20° и 10° соответственно. Моделирование считалось завершенным, когда центр массы тела змеи касался земли (приземление) или когда любой из углов ориентации превышал пороговое значения в 85°. Если это происходило, то планирование считалось нестабильным, т.е. не таким, как в природе. В процессе моделирования были протестированы как краткосрочная динамика (высота старта 10 м), так и длительную динамику (высота старта 75 м) с/без волнистости.
Модель показывает, что воздушная волнистость оказывает положительное влияние на характеристики планирования, обычно увеличивая горизонтальные и вертикальные расстояния, пройденные до того, как моделируемая змея станет нестабильной.
Моделирование летящей змеи, планирующей с волнистостью и без нее.
Короткие планирования с высотой запуска 10 м показали хороший коэффициент стабильности при наличии волнистости (94%). Если же волнистость не была включена в модель, то стабильными были лишь 50% полетов. Волнистость также увеличивает расстояние планирования (с 4 м до 4.3 м).
При моделировании планирования с высоты 75 м волнистость увеличила как горизонтальное, так и вертикальное расстояние до того, как проявляется нестабильность в 86% запусков. В данном случае волнистость также увеличивала расстояние полета в 92% запусках. Волнистость также увеличила среднее расстояние по горизонтали на 6.9 м.
Чтобы выяснить влияние амплитуды вертикальной волны и дорсовентрального изгиба на динамику скольжения, были использованы разные значения этих параметров в моделировании и рассмотрены полученные результаты.
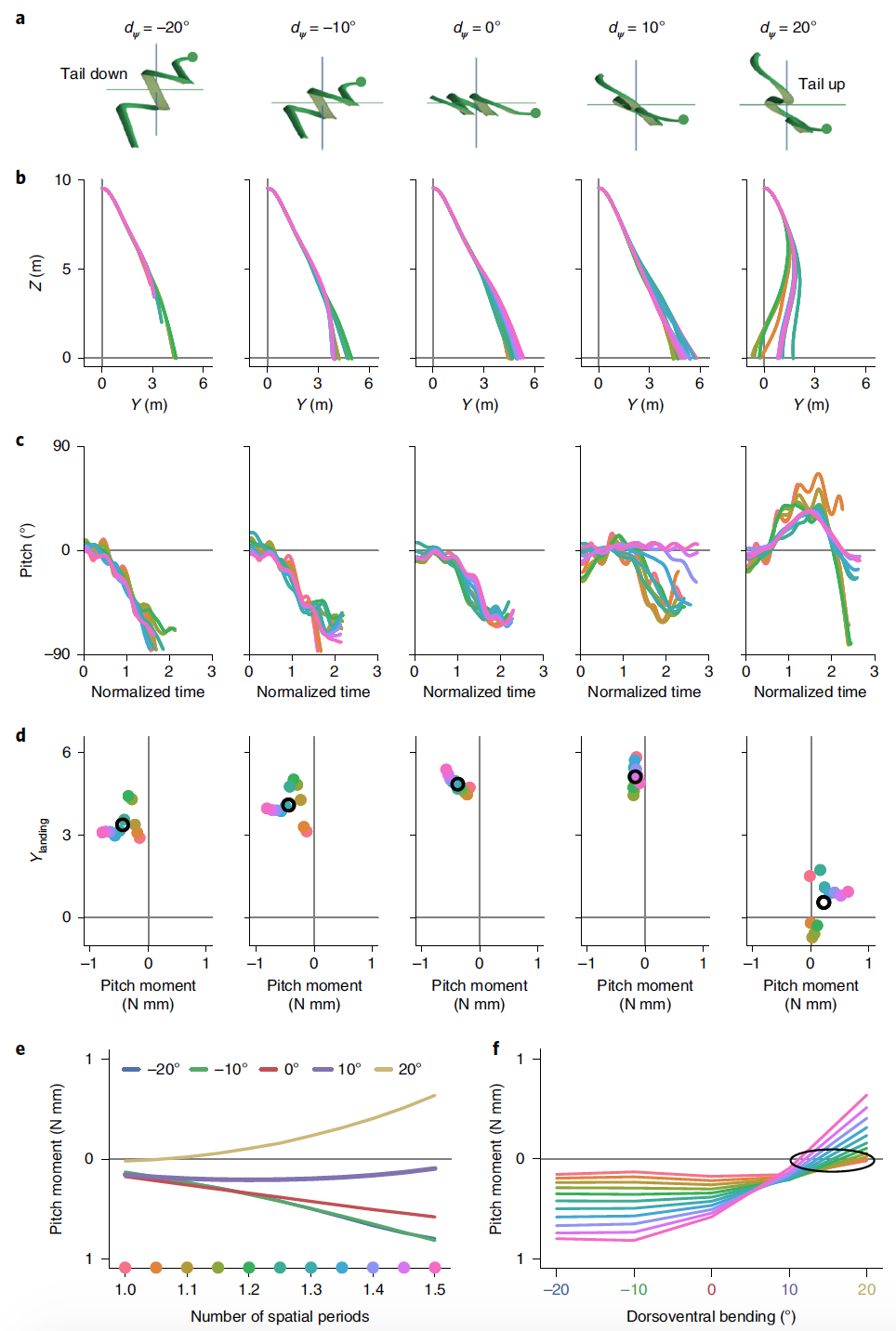
Изображение №5
Было смоделировано планирование с ψm = 0°, 10° и 20° и дорсовентральным изгибом от -20° до 20° с шагом в 10° (5а) для 11 различных форм тела.
Вертикальные колебания оказывают относительно небольшое влияние на траекторию планирования, тогда как дорсовентральный изгиб оказывает значимое влияние.
Совершенно плоская змея (ψm = 0°), чего никогда не наблюдалось во время экспериментальных испытаний, показала ожидаемо наихудшие результаты. Увеличение амплитуды вертикальной волны повышало эффективность планирования из-за скручивания поперечного сечения в плоскости, обеспечивающего более выгодный угол для создания силы (2j).
В отличие от амплитуды вертикальной волны дорсовентральный изгиб оказал заметное влияние на характеристики планирования, особенно на тангаж.
При ψm = −20° с задней частью тела ниже головы планирование не было неглубоким, вместо этого оно становилось нестабильным по высоте до падения на 10 м. При ψm = 20 ° с задней частью тела выше головы траектория изогнута назад, при этом некоторые формы тела приземляются позади места прыжка. Столь неудачное планирование обосновано наклоном тела вверх. Тем не менее, планирования с вышеуказанными параметрами обладали неплохой вращательной устойчивостью.
Для проверки связи между дорсовентральным изгибом тела, качкой и характеристиками планирования было проведено моделирование без вращения. Вместо решения связанной нелинейной системы уравнений №4 и №5 ученые провели выборку аэродинамических сил на разных фазах тела в течение цикла волнистости. Далее сюда интегрировали уравнение №4, и рассчитали положение и скорость центра массы.
По сути, эта манипуляция представляет собой эксперимент «виртуальной аэродинамической трубы», в котором динамическая модель используется для расчета распределенных сил, действующих на тело при его ускорении. Этот метод позволяет устранить связь поступательного и вращательного движения, чтобы количественно определить отдельные аэродинамические и инерционные вклады во вращательное движение.
При увеличении дорсовентрального изгиба от -20° до 10° позиция посадки моделируемой змеи увеличивается по мере того, как средний шаг тангажа увеличивается в направлении нуля (5d). При дорсовентральном изгибе 20° усредненный по фазе момент тангажа становится положительным, и характеристики планирования снижаются.
Для каждого угла дорсовентрального изгиба эффективность планирования и средний наклонный момент также зависят от используемой формы, в частности от количества пространственных периодов и амплитуды горизонтальной волны. Для любой формы тела в момент планирования дорсовентральный изгиб оказывает большое влияние на средний момент тангажа, и с увеличением числа пространственных периодов моменты расходятся, становясь более положительными или отрицательными в зависимости от dψ.
Метки усредненных по фазе моментов тангажа на 5e соответствуют наклону вверх или наклону, показанному на 5c, и результирующим характеристикам планирования на 5b. На 5f показан, что для форм тела с наименьшим пространственным периодом средний момент тангажа будет наименьшим.
Из вышеописанных данных можно предположить, что вертикальная волна заставляет тело сворачиваться вне плоскости, изменяя локальную ориентацию «сплющенного крыла» (форма тела змеи во время планирования) с помощью потока воздуха. Дорсовентральный изгиб контролирует величину и знак аэродинамического основного момента, который воздействует на тело. Летающая змея может контролировать момент тангажа, изменяя во время полета угол изгиба дорсовентрального отдела или форму горизонтальной волны.
Следовательно, дорсовентральный изгиб тела играет крайне важную роль в стабильности планирования, удачной посадке и возможности менять траекторию планирования прямо во время его исполнения.

Изображение №6
Анализ фазы путем усреднения позволяет количественно оценить относительный вклад аэродинамических и инерционных моментов в динамику планирования.
Из уравнений №5 следует, что на ориентацию тела влияют как аэродинамические силы, так и изменяющееся распределение массы. Аэродинамический вклад (6а) увеличивается со временем по мере увеличения скорости, тогда как инерционный вклад (6b) остается постоянным. Оба момента являются периодическими, и только момент тангажа показывает ненулевое среднее значение по фазе.
Около осей тангажа и крена первоначально преобладают инерционные моменты, но в течение одного волнообразного цикла их вклад быстро уменьшается. Инерционные моменты рыскания, как правило, на порядок больше аэродинамических моментов рыскания и больше, чем инерционные моменты вокруг других осей. Инерционные моменты рыскания возникают из-за горизонтальной волны большой амплитуды и широкой S-образной формы тела. Этот результат говорит о том, что летающие змеи могут использовать инерционное вращение в качестве механизма маневрирования.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
А желающие ознакомится с программным обеспечением, использованным для анализа планирования летающей змеи, могут перейти по этой ссылке.
Эпилог
В данном исследовании ученые использовали новейшие методики захвата движения и трехмерного моделирования, что позволило им создать анатомически точную модель летающей змеи.
Понять динамику полета птицы когда-то тоже было сложно, однако она не озадачивала ученых так сильно, как это делает летающая змея. В природе существует не так и много примеров бескрылых полетов, и все они сопряжены с и использованием нестандартных механизмов, позволяющих животному планировать, а не падать камнем на землю.
В случае летающих змей очень важную роль играет волнистость, которая наблюдается в движении ползающих и плавающих змей. Дополнительным механизмом стабилизации планирования является корректировка дорсовентрального угла изгиба тела. Объединив воедино эти элементы, летающие змеи способны перелетать с дерева на дерево, точно зная место будущей посадки.
Авторы сего труда считают, что их данные не только позволили нам лучше понять повадки украшенных древесных змей, но и получить дополнительное вдохновение для создания змееподобных роботов. Да, такие роботы уже есть. Они ползают, могут перемещаться по сложным поверхностям и проникать в труднодоступные места, но могут ли они летать?
С такими рассуждениями наш мир скоро будет похож на город машин из «Матрицы», где по стенам ползали крайне необычные (и слегка пугающие) роботизированные существа, назначение которых было сложно понять. Желание человека сделать робо-версию всего, что его окружает, нельзя журить. Такова наша природа — все понять, все знать, уметь создавать то, что до нас прекрасно делала природа. Если от роботизированных змей, пауков, собак и других робо-зверей будет намного больше пользы, чем вреда — такие исследования полностью оправданы.
Благодарю за внимание, оставайтесь любопытствующими и отличных всем выходных, ребята! 🙂

