Когда-то письма были самым распространенным методом передачи данных. Но на смену аналоговому миру пришел цифровой. Практически у каждого в кармане имеется устройство, позволяющее передавать и короткое сообщение, и снимок, и видео/аудио, и даже полное собрание произведений Дарьи Донцовой (а это немало). Даже оформление онлайн-покупки является своего рода обменом информации (платежные данные, ФИО и т.д.). Однако с эволюцией передачи данных эволюционировали и методы ее перехвата. Каждый раз, когда появляется новая система безопасности, направленная на борьбу с уже существующей системой взлома, на свет появляется новая система взлома, способная перехитрить эту систему безопасности. Такой вот каламбурный нескончаемый цикл. И вот ученые из Женевского университета опубликовали труд, в котором утверждают, что нашли идеальный способ обезопасить процесс передачи данных, применив при этом доказательство с нулевым разглашением. В чем суть данной концепции, как работает новый метод шифрования, и насколько он эффективен? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.
Основа исследования
Дабы очертить границы своего исследования, ученые в своем докладе описывают вполне житейский случай. Допустим, вы приехали в страну, где никогда не были. Желая обзавестись местными деньгами, вы идете к ближайшему банкомату, вводите нужные данные и снимаете наличные. Ни банкомат, ни банк, который им владеет, вам не знакомы. Зачем же тогда вы передали секретную личную информацию добровольно? А затем, чтобы получить деньги. И тут ученые задаются вопросом — можно ли создать метод идентификации без необходимости передавать личную информацию?
И тут на сцену выходит концепция «доказательство с нулевым разглашением». Сухое определение гласит: интерактивный криптографический протокол, позволяющий одной из взаимодействующих сторон («verifier» — проверяющей) убедиться в достоверности какого-либо утверждения (обычно математического), не имея при этом никакой другой информации от второй стороны («prover» — доказывающей). Ярким примером такой концепции является криптографический алгоритм RSA, в котором математическим секретом является разложение на два огромных простых числа еще большего числа.
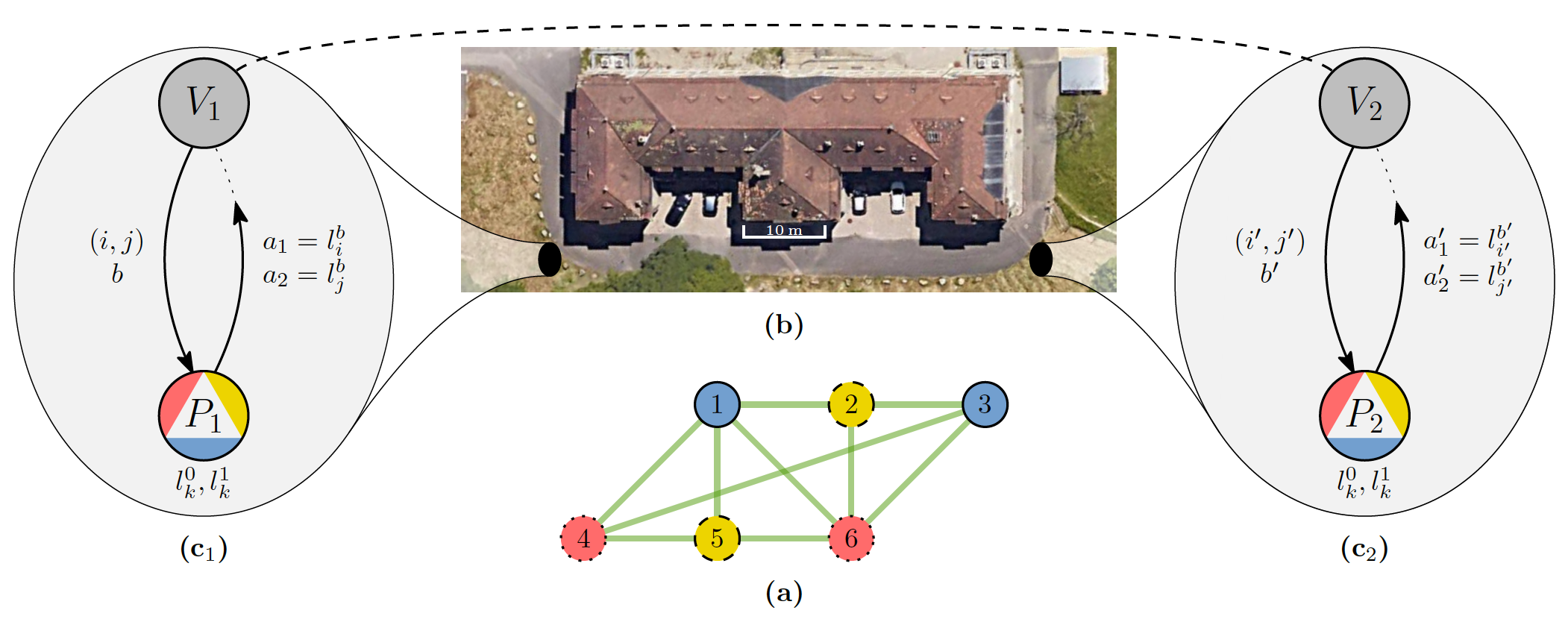
Изображение №1
В своей работе ученые рассматривают проблему трехкратной раскраски графов: образец представляет собой граф (узлы и ребра, соединяющие некоторые из них друг с другом), а доказательство трехцветности присваивает каждой вершине один из трех возможных цветов таким образом, что любые две вершины, соединенные ребром, имеют разный цвет (1a).
Некоторые графы могут быть трехцветными, некоторые — нет, и общая проблема определения того, является ли граф трехцветным, не имеет известного эффективного решения. Однако с помощью раскраски очень легко эффективно проверить, присвоены ли конечным точкам каждого ребра разные цвета. По этой причине трехцветность является проблемой в NP* — классе всех проблем, которые можно эффективно проверить при наличии решения.
Класс NP* — множество задач разрешимости (когда ответ на задачу «да» или «нет)», решение которых возможно проверить на машине Тьюринга за время, не превосходящее значения некоторого многочлена от размера входных данных, при наличии некоторых дополнительных сведений.
Более того, трехцветность является NP-полной, так как пример любой проблемы в NP может быть эффективно смоделирован примером трехцветной раскраски, так будто последняя была в классе P*. В итоге было бы равенство P = NP*, что является до сих пор одной из самых известных нерешенных проблем теории алгоритмов.
Класс P* — множество задач, для которых существуют «быстрые» алгоритмы решения, время работы которых полиномиально зависит от размера входных данных.
Проблема равенства P = NP*: если положительный ответ на какой-то вопрос можно довольно быстро проверить (за полиномиальное время), то правда ли, что ответ на этот вопрос можно довольно быстро найти (также за полиномиальное время и используя полиномиальную память)? Другими словами, действительно ли решение задачи проверить не легче, чем его отыскать?
Доказательство с нулевым разглашением для трехцветной раскраски предполагает существование односторонних функций, то есть функций, которые могут быть эффективно вычислены, но для которых невозможно найти прообраз конкретного выхода («Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems»).
Доказательство с нулевым разглашением гарантирует, что при участии в таком взаимодействии доказывающая сторона (prover) убедит проверяющую (verifier) в действительности утверждения, когда оно действительно достоверно (полнота), не убедит проверяющего, когда оно недействительно (надежность). Считается, что доказательство с нулевым разглашением для любой NP-полной задачи, такой как трехцветность, невозможно без этого дополнительного вычислительного предположения.
Проблема в том, что данная функция нежелательна, поскольку она значительно ослабляет долгосрочную безопасность таких протоколов с нулевым разглашением, которые используются, например, в некоторых криптовалютах. Это может иметь важные последствия, поскольку безопасность будет полностью поставлена под угрозу, если конкретная односторонняя функция, используемая в протоколе, в последствии будет обнаружена как эффективно обратимая.
При этом, как отмечают ученые, есть возможность создать протоколы с нулевым разглашением без каких-либо расчетных предположений. Фундамент этой теории, предложенной в труде «Multi-prover interactive proofs: how to remove intractability assumptions», заключается в том, чтобы обобщить интерактивную модель доказательства таким образом, чтобы несколько доказывающих пытались убедить проверяющего в трехцветности графа в идеальном условии нулевого разглашения без каких-либо дополнительных предположений. Данный метод напоминает перекрестный допрос, когда двух свидетелей допрашивают раздельно, ибо так им будет гораздо сложнее скоординировано солгать.
Ключевое различие между сценарием с несколькими доказывающими и исходным определением интерактивного доказательства заключается в возможности предотвратить общение нескольких доказывающих друг с другом, при этом один доказывающий всегда может разговаривать сам с собой. Это, естественно, предполагает использование пространственного разделения для обеспечения невозможности общения, по крайней мере, в течение некоторого короткого периода времени. Учитывая принципы теории относительности (а именно, ничто не может двигаться быстрее скорости света) и отправляя запросы к разным доказывающим одновременно, можно получить короткое временное окно, в течение которого физически не могут передавать друг другу сигналы.
В рассматриваемом нами сегодня труде ученые представили метод практической реализации релятивистских доказательств с нулевым разглашением для NP-полной задачи (трехцветность). Было проведено два эксперимента. В первом были использованы GPS часы для синхронизации двух проверяющих, а затем был реализован протокол проверки на расстоянии 400 метров. Во втором эксперименте между двумя проверяющими было оптоволокно, а расстояние составляло 60 метров. В обоих случаях полное время работы составляло около 1 секунды.
Первый опыт показывает, что протокол на больших расстояниях довольно прост, поскольку широкое релятивистское разделение требует только умеренной скорости со стороны проверяющих. Второй опыт демонстрирует явный потенциал для различных приложений. Ученые также отмечают, что безопасность обеспечивается релятивистскими ограничениями и не полагается на какие-либо вычислительные гипотезы, такие как существование односторонних функций.
Подготовка к экспериментам
В опытах использовался следующий тип доказательства с нулевым разглашением: пусть (V; E) — конечный неориентированный граф с конечным множеством вершин (V) и ребер (E), т.е. неупорядоченных пар (различных) вершин. Далее предполагается, что этот граф трехцветный (1a), цвета при этом обозначаются как 0, 1 и 2.
В протоколе задействовано 2 проверяющих и 2 доказывающих. Первоначально два доказывающих предварительно согласовывают случайные трехцветные раскраски ck(n) ∈ {0, 1, 2} для k ∈ V и n, обозначающего число раундов. Для каждой вершины k доказывающие также выбирают две разметки l0k и l1k, удовлетворяющие l0k + l1k = ck.
Каждый раунд (1c) состоял из следующих этапов:
- каждый проверяющий предоставляет своему доказывающему ребро (i, j) ∈ E и бит b ∈ {0, 1};
- каждый доказывающий отвечает на lbi и lbj;
- два проверяющих проверяют ответы доказывающих.
Тесты проверяющих проходят двумя разными путями. С одной стороны, проверяющие могут оценить, действительно ли доказывающие знают, что граф трехцветный. Этот тест выполняется, когда оба проверяющих отправляют одно и то же случайное ребро e = (i, j) = (i’, j’) = e’ ∈ E и когда b ≠ b’.
Ответы (a1, a2) и (a’1, a’2) двух доказывающих принимаются тогда и только тогда, когда a1 + a’1 ≠ a2 + a’2. Это нацелено на то, чтобы доказывающие доказали, что они знают, что граф трехцветный.
Проверяющие также могли проверить последовательность ответов доказывающих. Когда отправленные ребра разделяют по крайней мере одну вершину (скажем, i = i’) и когда отправленные биты равны (b = b’), верификаторы принимают ответы доказывающих, если они равны (a1 = a’1). Этот тест не позволяет доказывающим отвечать, игнорируя запрошенные ребра, а нацеливаться только на прохождение предыдущей проверки.
Для «честных» (т.е. подлинных) проверяющих и «честных» доказывающих протокол всегда приводит к принятию. Это свойство протокола называется полнотой.
Для честных проверяющих и нечестных доказывающих (когда график не является трехцветным), надежность относится к тому, что проверяющие могут с очень высокой вероятностью выявить обман при выполнении многих раундов. Другими словами, если ответы одного доказывающего (к примеру, P2) достигают своего соответствующего проверяющего (V2) до того, как вопрос другого проверяющего (V1) каким-либо образом мог попасть туда, то этот доказывающий (P2) обязан дать ответ, не зная, о чем спрашивали другого доказывающего (P1).
Для нечестных проверяющих (пытающихся получить какое-либо знание о трехцветной раскраске) и честных доказывающих свойство нулевого разглашения сводится к тому, что проверяющие не получают никаких данных при взаимодействии с доказывающими.
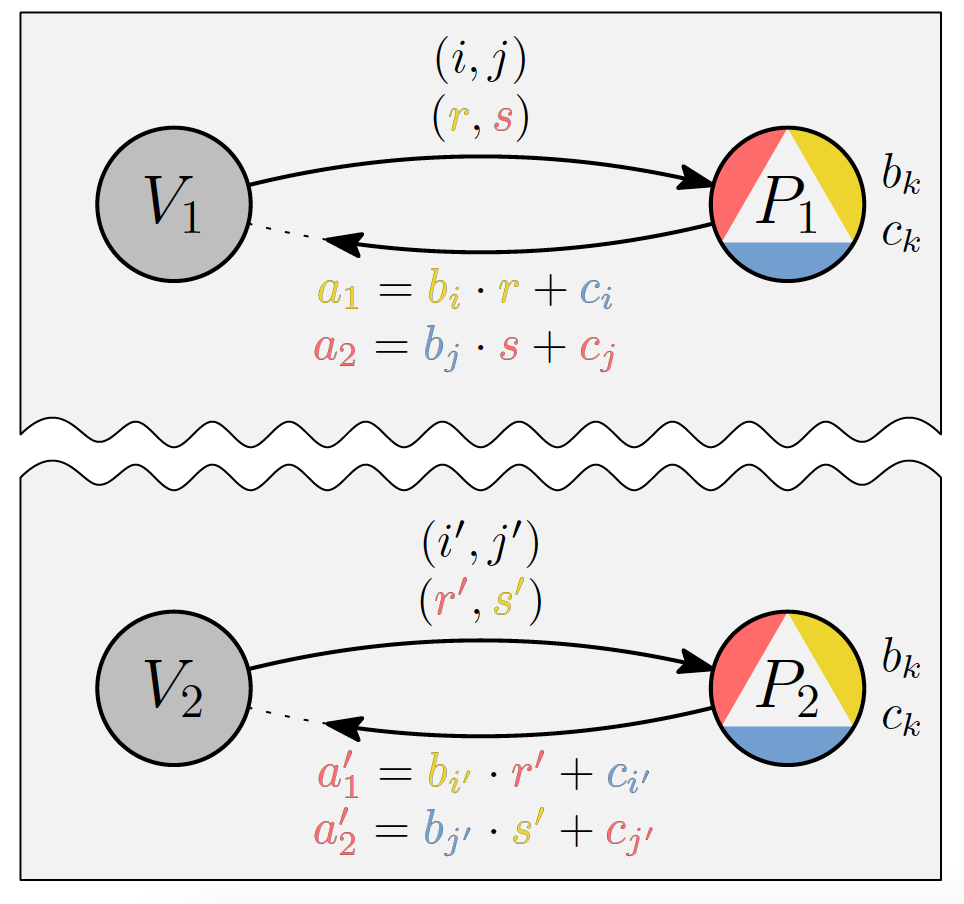
Изображение №2: пример одного раунда работы протокола.
С теоретической точки зрения проблема трехцветности является NP-полной. Это означает, что нахождение решения (трехцветная раскраска) невозможно при полиномиальной сложности относительно размера задачи, но проверка решения может быть выполнена при полиномиальной сложности. Тот факт, что эта задача является NP-полной, означает, что она может моделировать с полиномиальной сложностью любую другую NP задачу.
Для реализации протокола, учитывая все вышесказанное, необходим конкретный граф вместе с его трехцветной раскраской. И тут возникает небольшая загвоздка — хоть задача в целом и «сложна», существуют алгоритмы, способные ее решить. Следовательно, необходимо использовать достаточно большой граф.
4-критический граф* изначально трехцветным не является, но если удалить одно любое ребро, то в результате будет необходимый для протокола трехцветный граф.
Критический граф* — граф, в котором удаление любой вершины или ребра приводит к уменьшению хроматического числа* графа.
Хроматическое число* — минимальное число цветов, в которые можно раскрасить вершины графа так, чтобы концы любого ребра имели разные цвета.
Граф, используемый в следующих экспериментах, имел |V| = 588 вершин и |E| = 1097 ребер, так что для достижения параметра безопасности k = 100 требуется около миллиона раундов.
При реализации протокола использовалось две пары проверяющий/доказывающий, о чем уже говорилось ранее. Также использовались и FPGA (от field-programmable gate array, т.е. программируемая пользователем вентильная матрица), позволяющие уменьшить задержки связи, ускорить вычисления и повысить степень надежности.
Важно и то, что в экспериментах было задействовано две шкалы времени: скорость обмена между проверяющими и доказывающими и частота повторения раундов. Первая шкала устанавливает минимальное расстояние, требуемое между двумя точками, и ограничивается скоростью вычислений на стороне доказывающего. Вторая шкала определяет время, которое требуется протоколу для достижения заданного параметра безопасности.
Результаты экспериментов
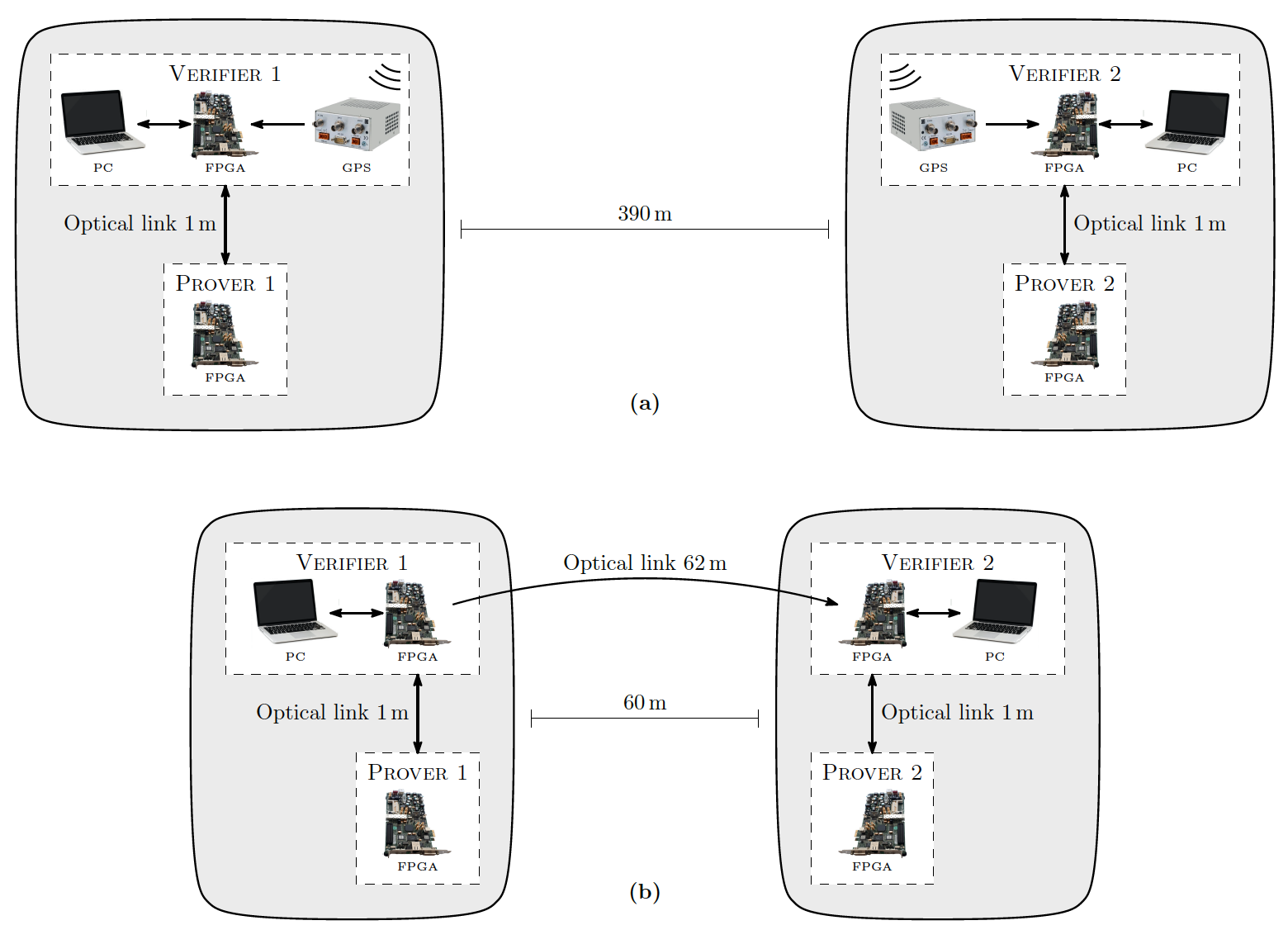
Изображение №3: два варианта конфигурации проведенных опытов.
Первый опыт подразумевал большое расстояние между двумя проверяющими и двумя доказывающими, размещенными в разных зданиях на расстоянии 390 м друг от друга. Синхронизация обеспечивалась GPS часами.
Оба проверяющих отправляли своему соответствующему доказывающему поток запросов с частотой 0.3 МГц. Как только доказывающие получают запрос, они вычисляют свои ответы на основе своих общих данных (1c).
Принимая во внимание неточность системы, общее время, прошедшее между передачей запросов проверяющих и получением ответов доказывающих, составляло 840 нс. Весь протокол с одним миллионом раундов выполнялся примерно за 3 секунды.
Второй опыт подразумевал малое расстояние между двумя проверяющими и двумя доказывающими, размещенными на расстоянии 60 м друг от друга (1b). Сигнал запроса передается от одного проверяющего второму. Как только сигнал доходит до цели, второй проверяющий отправляет запрос доказывающему, к которому он подключен. При этом первый проверяющий задерживает отправку своего собственного запроса на время, необходимое второму проверяющему на это действие. Затем доказывающие, получив запрос, обкатывают и отправляют обратно ответ. В целом один раунд выполняется максимум за 192 нс. При частоте повторения 3 МГц весь протокол с одним миллионом раундов выполняется менее чем за секунду.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых.
Эпилог
В данном труде ученые продемонстрировали, что релятивистское доказательство с нулевым разглашением для NP-полной задачи трехцветной раскраски возможно на практике даже для малых расстояний. Протокол проверки построен на базе двух пар проверяющий-доказывающий и трехцветного графа.
Чтобы подтвердить свою личность, доказывающим нет нужды предоставлять какой-то код, достаточно просто продемонстрировать проверяющему, что они знают, как сделать определенный граф трехцветным (удалив при этом какое-то его ребро).
Проверяющие случайным образом выбирают большое число пар узлов на графе, а затем отправляют запрос своим доказывающим — какого цвета этот узел. Поскольку эта проверка выполняется почти одновременно, доказывающие не могут коммуницировать друг с другом во время теста и, следовательно, не могут обмануть проверяющих. Таким образом, если два цвета всегда различны, проверяющие убеждаются в надежности доказывающих, так как они действительно знают трехцветную раскраску этого графа.
На первый взгляд все это кажется каким-то сложным и запутанным (так и есть, на самом деле). Однако аналогия с перекрестным допросом, предложенная учеными, отлично поясняет принцип работы их протокола. Когда одновременно допрашиваются оба доказывающих, они не могут обмениваться информацией, чтобы сфабриковать ответ. Во время практических опытов протокол выполнял порядка трех миллионов раундов проверки менее чем за 3 секунды. При этом расстояние между парами проверяющий-доказывающий составляло 60 метров, что гарантировало отсутствие коммуникации между доказывающими. В будущем же ученые намерены сократить это расстояние до одного метра.
Несмотря на некоторую сырость разработки, ее можно использовать уже сейчас (например, между отделениями банка). Подобная система гарантирует невероятно высокую степень безопасности передачи информации. Ученые, не скрывая гордости за свой труд, считают, что такую систему взломать попросту невозможно. Громкие заявления оптимистически настроенных ученых или же фактическая действительность, проверенная на практике — покажет время.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. 🙂
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?


