Предлагаю поразмять мозги и как в прошлом году, порешать задачки с математической олимпиады в комментариях к этой статье. Задачек 6 штук, и на них отводилось 2 дня по 4,5 часа.
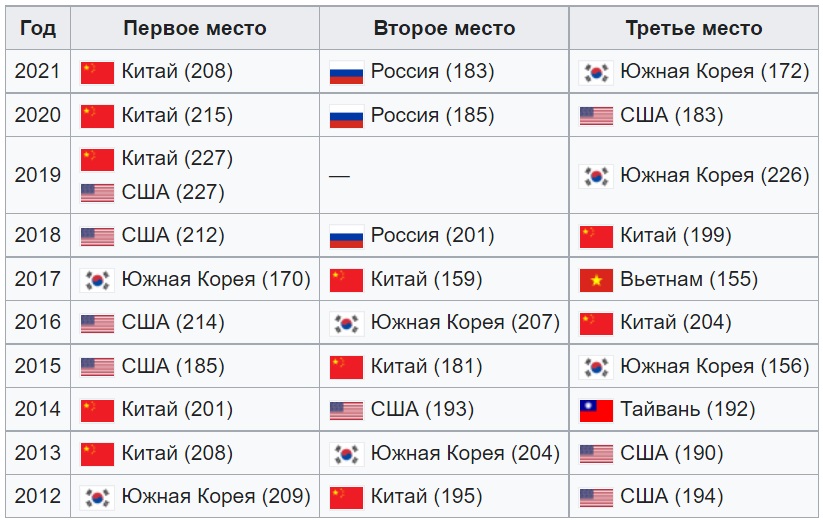
Этим летом в Питере прошла 62-я Международная математическая олимпиада с вот какими итогами:
- Первое место заняла команда Китая, завоевавшая шесть золотых медалей (208 баллов).
- Российские школьники заняли второе место с пять золотых и одной серебряной медалью (183 балла)
- На третьем месте южнокорейская команда с пятью золотых и одной серебряной медалью (172 балла)
Первая такая олимпиада прошла в 1959 году в Румынии, и тогда в ней принимали участие представители всего семи стран. В 2021 году в олимпиаде участвовали более 619 школьников из 107 стран.
- Иван Бахарев (10 класс, Санкт-Петербург) — золотая медаль;
- Айдар Ибрагимов (11 класс, Казань / Москва) — золотая медаль;
- Матвей Исупов (11 класс, Ижевск) — золотая медаль;
- Андрей Шевцов (11 класс, Москва) — серебряная медаль;
- Данил Сибгатуллин (11 класс, Казань / Москва) — золотая медаль;
- Максим Туревский (10 класс, Санкт-Петербург) — золотая медаль, абсолютное второе место в общем рейтинге.
День 1
Время на работу: 4 часа 30 минут.
Каждая задача оценивается в 7 баллов
Задача 1
Дано целое число n > 100. Ваня написал числа n, n+ 1,…, 2n на n+ 1 карточке, каждое по одному разу. Затем он перемешал колоду из этих карточек и разделил её на две стопки. Докажите, что хотя бы одна из двух стопок содержит две карточки, сумма чисел на которых — точный квадрат.
Задача 2
Докажите, что для любых вещественных чисел x1,…, xn выполняется неравенство
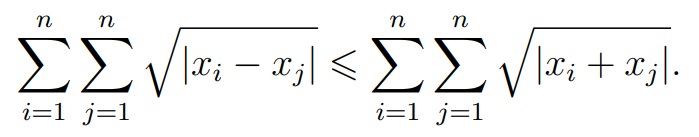
Задача 3
Точка D внутри остроугольного треугольника ABC, в котором AB > AC, такова, что
∠DAB = ∠CAD. Точка E на отрезке AC такова, что ∠ADE = ∠BCD; точка F на отрезке AB
такова, что ∠F DA = ∠DBC; точка X на прямой AC такова, что CX = BX. Точки O1 и O2 — центры
описанных окружностей треугольников ADC и EXD соответственно. Докажите, что прямые BC,
EF и O1O2 пересекаются в одной точке.
День 2
Время на работу: 4 часа 30 минут.
Каждая задача оценивается в 7 баллов
Задача 4
Дана окружность Γ с центром I. Выпуклый четырёхугольник ABCD таков, что каждый из отрезков AB, BC, CD и DA касается Γ. Пусть Ω — описанная окружность треугольника AIC. Продолжение отрезка BA за точку A пересекает Ω в точке X, продолжение отрезка BC за точку C пересекает Ω в точке Z. Продолжения отрезков AD и CD за точку D пересекают Ω в точках Y и T соответственно.
Докажите, что AD + DT + T X + XA = CD + DY + Y Z + ZC.
Задача 5
Чип и Дейл собрали на зиму 2021 орешек. Чип пронумеровал орешки числами от 1 до 2021 и вырыл 2021 маленькую ямку вокруг их любимого дерева. На следующее утро он обнаружил, что Дейл положил в каждую ямку по орешку, ничуть не беспокоясь о порядке. Расстроившись, Чип решил переупорядочить орешки посредством следующей последовательности из 2021 действия: во время k-го действия он меняет местами орешки, соседние с орешком под номером k.
Докажите, что найдётся такое число k, что во время k-го действия поменялись местами орешки с номерами a и b такими, что a < k < b.
Задача 6
Дано целое число m > 2. В конечном множестве A, состоящем из (не обязательно положительных) целых чисел, нашлись такие подмножества B1, B2, B3,…, Bm, что при каждом k = 1, 2,…, m сумма элементов множества Bk равна mk. Докажите, что A содержит хотя бы m/2 элементов.
- Второе место на Международной математической олимпиаде 2020
- Международная математическая олимпиада 2020 (решаем в комментах)
- 100 уроков Математики Алексея Савватеева
