
Знаменитая поговорка «вода и камень точит» говорит о том, как даже самые малозаметные, но постоянные и настойчивые действия могут в последствии иметь значимый эффект. Однако это фигуральное выражение имеет под собой вполне реальный процесс, который обусловлен теми или иными физическими и/или химическими свойствами материалов. Ученые из Миннесотского университета (США) решили выяснить, что именно происходит, когда капли воды падают на твердую поверхность. Как именно вода побеждает камень, какие скрытые силы действуют в момент их взаимодействия, и как полученные из наблюдений данные можно применить в будущем? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.
Основа исследования
В далеком пятом веке до н.э. древнекитайский философ Лао-цзы отметит способность воды разрушать твердые вещества. Это наблюдение породило знаменитую поговорку, дожившую и до наших дней.

Изображение №1
Технологический прогресс привел к тому, что ученые начали проявлять интерес к процессам и явлениям, которые ранее либо невозможно было изучить детально, либо они казались незначительными и неважными. К примеру, появление высокоскоростной съемки позволило лучше понять, что происходит в момент падения капли на какую-то поверхность.
Однако, как отмечают ученые, ограничиваясь прямой визуализацией, большинство текущих исследований были сосредоточены на кинематике падающих капель (порог разбрызгивания, максимальный диаметр растекания и время контакта), а также на формирование амортизирующих слоев воздуха под каплями. При этом было проведено очень мало экспериментов по изучению динамических свойств «ударных» капель, которые непосредственно ответственны за эрозию, вызванную падением капель на материал.
В попытках заполнить этот пробел в знаниях ученые выяснили, что необычная способность ударной капли вызывать эрозию не может быть связана только с ее ударной силой, поскольку максимальная ударная сила, вызванная миллиметровой каплей воды, падающей вблизи ее конечной скорости, очень мала. Стоит также учесть и растекание капли, от чего среднее ударное давление капли будет еще меньше.
Капля воды, падающая на песочную поверхность.
Таким образом, вместо силы удара или средних ударных напряжений* эрозионная способность удара капли должна быть обусловлена уникальной пространственно-временной структурой ее ударных напряжений, а также динамической реакцией ударяемых подложек на такие напряжения.
Напряжение* — в данном случае имеется ввиду именно механическое напряжение, которая выражает внутренние силы, которые соседние частицы в непрерывной среде оказывают друг на друга.
В рассматриваемом нами сегодня труде ученые продемонстрировали новый метод — высокоскоростную микроскопию напряжений, позволяющую измерить ударное напряжение при контакте капли с твердой эластичной подложкой. Для реализации задуманного ученые использовали комбинацию различных методов визуализации: тяговая силовая микроскопия, высокоскоростная фотография и лазерно-листовая (одноплоскостная) микроскопия. Совокупность использованных инструментов позволяет отображать временную эволюцию распределения давления и напряжения сдвига под каплями миллиметрового размера во время быстрых ударов с большим пространственно-временным разрешением.
Подготовка к наблюдениям
В качестве подложки, на которую падали капли, выступил гель полидиметилсилоксана (PDMS от polydimethylsiloxane) с внедренными в него флуоресцентными частицами полистирола с низкой концентрацией (0.23% об./об.) диаметром 30 мкм. Эти частицы служили индикатором для отслеживания деформации геля при ударе. Поверхность PDMS геля гидрофобна с краевым углом смачивания водой ~90°. Модуль Юнга (модуль упругости) геля составлял Е=100 кПа.

Изображение №2
Тонкий лазерный луч (в виде плоскости / листа) толщиной 30 мкм освещал гель сбоку и возбуждал флуоресцентные индикаторы внутри листа (2а). Луч был точно отрегулирован так, чтобы быть перпендикулярным поверхности удара и проходить через центр ударных капель. Высокоскоростная камера, сфокусированная на листе, фиксировала движение индикаторов со скоростью 40000 кадров в секунду. Смещение индикаторов отслеживалось посредством цифровой корреляции изображений (DIC от digital image correlation). Исследуемая область 384 мкм на 384 мкм с перекрытием 70%, использованное в DIC, давало пространственное разрешение 115 мкм. Временное разрешение составляло 0.025 мс и было задано частотой кадров высокоскоростной фотосъемки.
Поля напряжений зависят от полей деформации, которые являются производными от полей перемещений, полученных из DIC. Процедура сглаживания необходима для того, чтобы уменьшить шум дифференцирования. Для получения непрерывно дифференцируемого поля перемещений из дискретного поля перемещений DIC был использован метод интерполяции посредством наименьших квадратов (MLS от moving least squares).
При малых деформациях компоненты деформации в цилиндрических координатах были таковы:

Предполагая, что гели ПДМС изотропны и линейны в соответствии с обобщенным законом Гука при малых деформациях, ученые рассчитали поля напряжений, используя линейное соотношение напряжение-деформация:

где λ = Eν/[(1 + ν)(1 − 2ν)] — коэффициент Ламе; G = E/[2(1 + ν)] — модуль сдвига; δij — дельта Кронекера; εb ≡ εzz + εrr + εθθ – объемная деформация; σrz дает касательное напряжение τ, тогда как σzz дает давление p.
Гели PDMS практически несжимаемы, а коэффициент Пуассона (ν) близок к 0.5, что приводит к большому λ. Но объемная деформация εb в этом пределе близка к 0. Следовательно, ударное давление не может быть точно определено произведением λεb в уравнении. Вместо этого было принято предположение о квазистационарном состоянии для расчета давления. Была выполнена проверка предположения путем сравнения силы инерции и силы упругости в процессе удара, а также путем сравнения экспериментальных и численных результатов по ударному давлению при падении твердой сферы.
В качестве калибровки и основы для сравнения сначала были измерены давление и напряжение сдвига, вызванные ударом стальной сферы диаметром D = 3.16 мм при скорости удара U = 0.49 м/с, и сравнение этих результатов с теми, что были получены в ходе моделирования методов конечных элементов. Экспериментальные измерения хорошо согласуются с результатами моделирования, подтверждая точность высокоскоростной микроскопии напряжений (2b).
Капли для опытов состояли из водного раствора йодида натрия (60 %), который имеет плотность ρ = 2.2 г/мл и вязкость η = 1.12 мПа·с. Поверхностное натяжение раствора было σ ≈ 81.3 мН/м по данным тензиометрии висячих капель, что несколько больше, чем у воды. Диаметр капель и скорость их удара о подложку были зафиксированы. Капли диаметром D = 3.49 мм падают на поверхность PDMS геля при U = 2.97 м/с, что дает число Рейнольдса Re = ρUD/η = 20 360 и число Вебера We = ρDU2/σ = 833. Таким образом, в ударе капли на ранних этапах преобладает инерция жидкости.
Наблюдение было сосредоточено именно на ударе капель о гель, когда напряжение сдвига и давление ударяющихся капель достаточно высоки.
Результаты наблюдений
Изображение №3
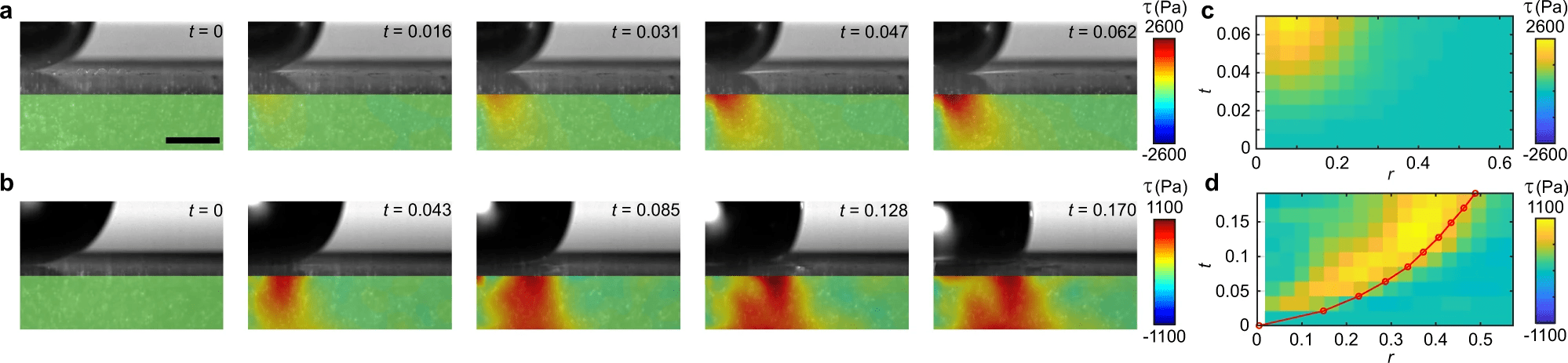
Поверхностная эрозия является прямым следствием напряжения сдвига при ударе капли. На 3a и 3b показано сравнение временной эволюции напряжения сдвига при ударе твердой сферой и при ударе капли жидкости.
При ударе в обоих случаях быстро развивались пространственно неоднородные касательные напряжения. Однако в то время как положение максимального напряжения сдвига при ударе твердой сферы являлось стационарным вблизи оси удара при r = 0.095, то максимальное напряжение сдвига при ударе капли распространялось радиально с растекающейся каплей. Кимограммы поверхностного напряжения сдвига ( τ(r, z = 0, t) ) двух процессов удара показаны на 3c и 3d, что дополнительно подчеркивает быстрое распространение максимального напряжения сдвига при ударе капли.
Изображение №4
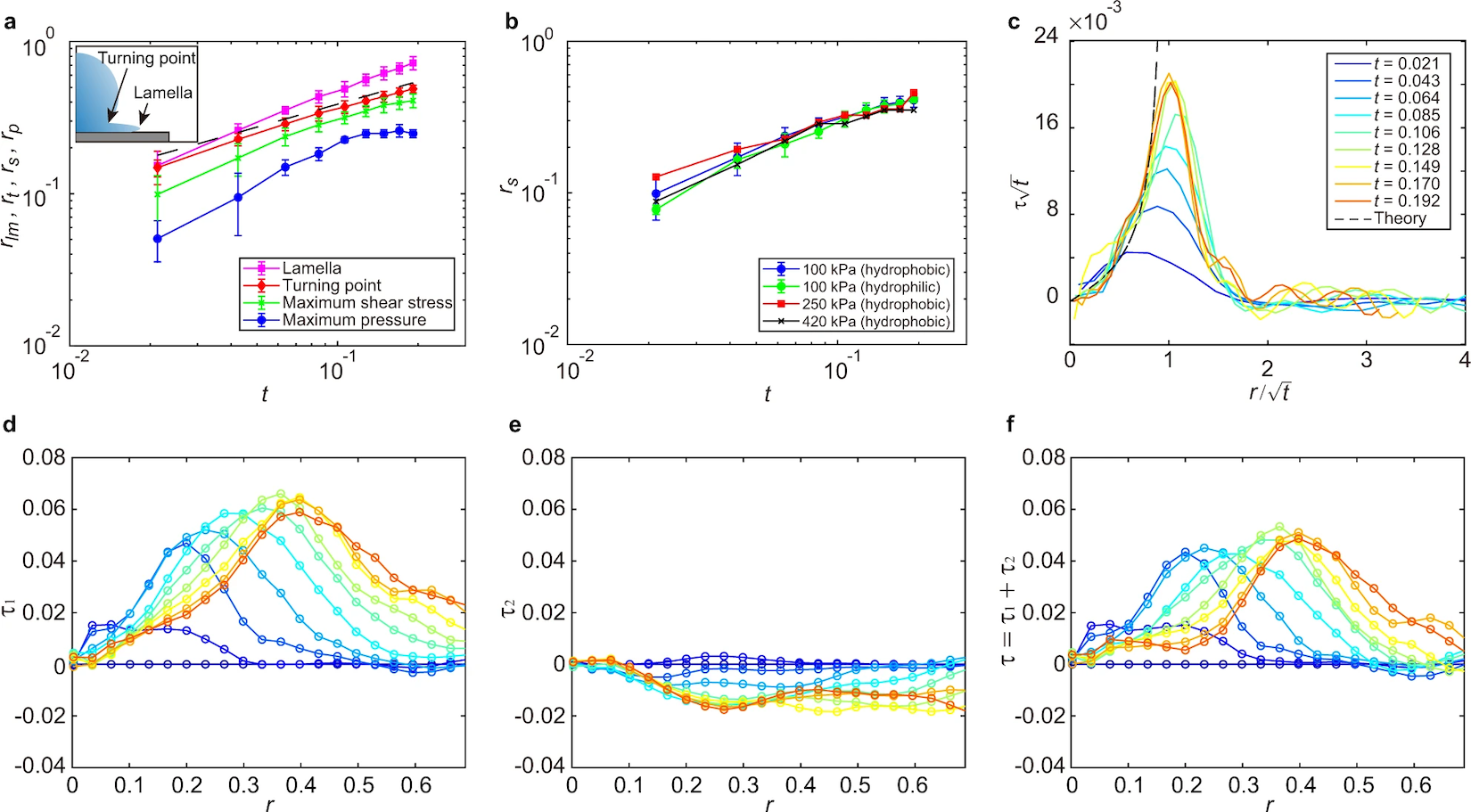
Чтобы понять происхождение максимального напряжения сдвига от удара капли, было проведено сопоставление положения максимального напряжения сдвига (rs) с формой ударяющихся капель (4а). Анализировалось две кинематические особенности: вершина расширяющейся ламель (rlm), т.е. растекающейся части капли после столкновения, и точка контакта (rt), где тело капли соединяется с корнем ламели (вставка на 4а). Важно отметить, что rt не является контактной линией капли.
Выброс ламели происходит около t ≈ We−2/3 = 0.010433, что короче временного разрешения проводимых экспериментов. В то время как rlm движется быстрее всего, rs следует за rt. Таким образом, максимальное напряжение сдвига возникает из-за сильного градиента скорости вблизи точки контакта, где поток быстро меняется с вертикального направления вниз (направление -z) внутри тела капли на горизонтальное радиальное направление (направление r) внутри узкой ламели. При этом положения максимального напряжения сдвига и точки контакта не зависят от смачиваемости или модуля Юнга PDMS гелей (4b).
В ранее проведенных исследованиях (Drop impact on a solid surface: short time self-similarity) было установлено, что касательное напряжение несжимаемых капель на бесконечно жестких подложках имеет автомодельную динамическую структуру при t→0+:
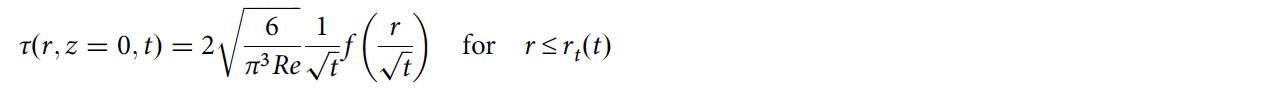
где масштабирующая функция f(x)=x/(3−2x2) диктует сингулярность конечного времени в точке контакта rt(t). Здесь τ(r, t) обезразмеривается инерционным давлением ρU2. В формуле c обозначает скорость звука в жидкости.
Основываясь на автомодельной гипотезе, была построена зависимость τ√t от r/√t (4c), которая показывает свертывание при малом r вдали от сингулярной области. С модифицированной функцией масштабирования f(x)=x/(1−x2) для подсчета различных временных масштабов rt и rs свернутые данные количественно согласуются с уравнением (пунктирная линия на 4c).
Таким образом, проведенное исследование предоставляет экспериментальные данные о распространении напряжения сдвига при ударе капли и демонстрирует самоподобную структуру напряжения сдвига на ранних этапах.
Несмотря на общее согласие с вышеуказанной формулой при r < rt, в проведенных экспериментах также обнаруживаются уникальные особенности удара капли по упруго деформируемым подложкам, отсутствующие при теоретическом рассмотрении удара капли по бесконечно жестким подложкам.
Касательное напряжение на поверхности упругой подложки определяется выражением τ = G(∂ur/∂z + ∂uz/∂r), где G — модуль сдвига подложки, а ur и uz — радиальное и вертикальное смещения поверхность подложки. Далее было установлено, что |∂uz/∂r| > |∂ur/∂z| (4d—4f), что свидетельствует о доминирующей роли вертикальной скорости ударяющейся капли в контактной области vz(r, z = 0) на касательное напряжение.
При ударе капли о бесконечно жесткую подложку vz(r, z = 0, t) = 0 из-за граничного условия непроникания, что неизбежно дает ∂uz/∂r = 0. Вместо этого напряжение сдвига при ударе капли о бесконечно жесткую подложку возникает из-за градиента радиальной скорости ∂vr/∂z в пограничном слое вблизи контактной поверхности. Поскольку uz(r, z = 0) в основном определяется распределением давления на поверхности контакта при высоких Re, этот вывод иллюстрирует внутреннюю связь между ударным давлением и напряжением сдвига при ударе капли об упругие подложки.
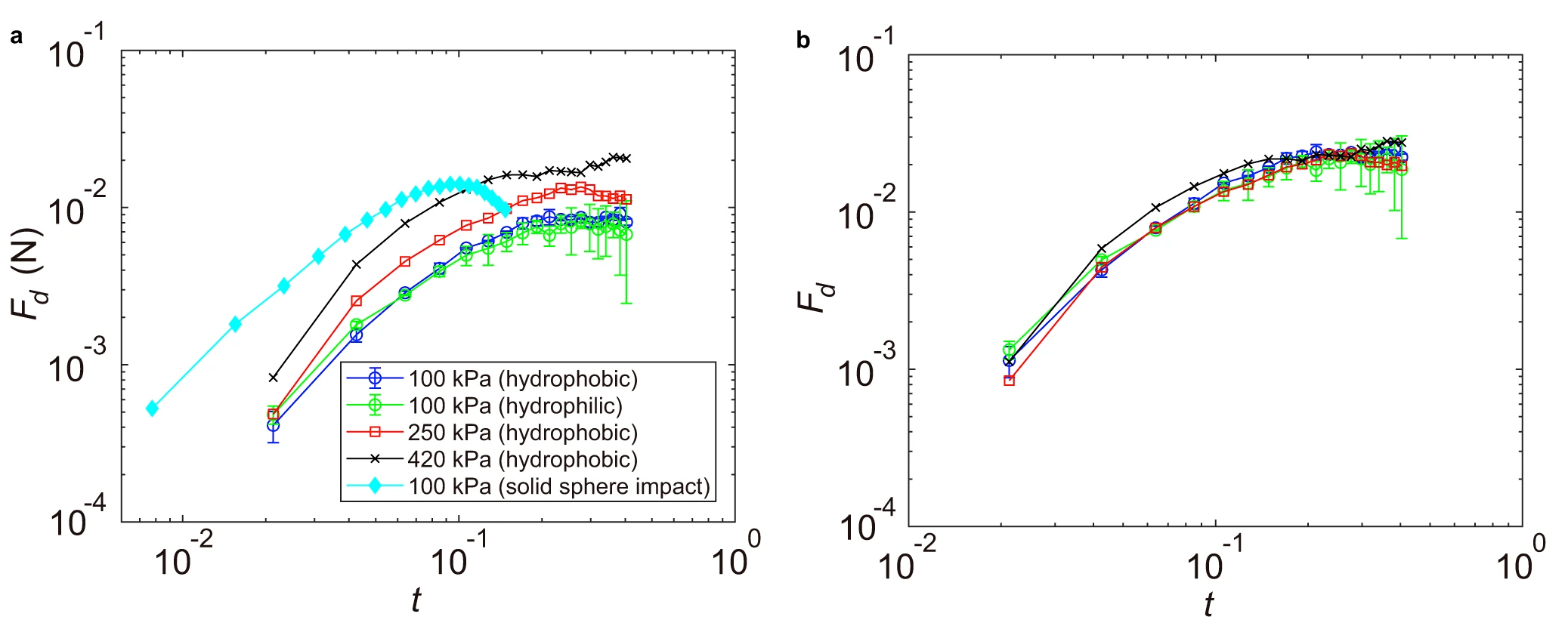
Эффект конечной жесткости ударяемой подложки проявляется и в силе сдвига падающих капель. Интегрируя напряжение сдвига по площади контакта, была получена сила сдвига Fd(t) = 2π ∫0rlmτ(r, z = 0, t)rdt, которая количественно определяет общую силу эрозии при ударе капли. Хотя Fd(t) не зависит от смачиваемости ударяемой поверхности, она возрастает с увеличением модуля Юнга (5a и 5b).
Изображение №5
Благодаря распределению максимального напряжения сдвига удар капли и удар твердой сферы демонстрируют сопоставимые пиковые силы сдвига при одинаковых условиях удара (5а).
Ученые отмечают, что, несмотря на большие экспериментальные ошибки из-за почти несжимаемости PDMS, распределение давления (то есть нормального напряжения) под ударяющими каплями p® также можно измерить с помощью высокоскоростной микроскопии напряжений.

Изображение №6
Подобно касательному напряжению, наблюдался нецентральный максимум давления, распространяющийся радиально с растекающейся каплей (6b и 6d). Динамика опять-таки сильно отличается от давления удара твердой сферы, где максимальное давление удара фиксируется на оси удара r = 0 (6a и 6c).
Интересно, что перед точкой контакта rt при tc ≈ 0.106 возникает отрицательное давление (6b и 6d). В то же время наблюдается распространение поверхностных возмущений на поверхности геля вдали от максимумов напряжения выше tc (7а).

Изображение №7
Оба эти факта предполагают образование поверхностной акустической волны в геле, т.е классической волны Рэлея. Волна Рэлея достигает точки контакта и высвобождается перед растекающейся каплей во взрывоподобном процессе выше tc, вызывая отрицательное давление и распространение поверхностных возмущений.
Более того, численное решение связанных уравнений качественно воспроизводит формирование ударно-индуцированной волны Рэлея от удара капли, где при tc ≈ 0.1 возникает острая поверхностная волна с четко выраженным пиком, распространяющаяся с VR (7c). Сильная и острая поверхностная волна создается механическим резонансом, возникающим, когда скорость максимумов напряжений приближается к скорости волны Рэлея вблизи tc. Такое резонансное явление не существует при падении твердой сферой со стационарными максимумами напряжений. В результате поверхностная волна Рэлея от удара твердой сферы является более диффузной.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
В рассмотренном нами сегодня труде ученые попытались установить силы, влияющие на эрозию материала, на который падает капля воды. Другими словами, ученые хотели с помощью измерений и вычислений предоставить объяснение знаменитой фразе «вода и камень точит».
Как оказалось, сила, генерируемая каплей, распространяется вместе с самой каплей, а не концентрируется только в точке непосредственного удара капли о поверхность. При этом скорость распространения капли в определенный момент превышает скорость звука, в результате чего формируется ударная волна. Следовательно, падающая капля действует как мини-бомбочка, высвобождающая энергию удара, которая со временем и вызывает эрозию материала.
Авторы исследования отмечают, что понимание того, как жидкостные капли воздействуют на твердые материалы, может способствовать разработке средств, снижающих или предотвращающих эрозию. В качестве примера они приводят обычную покраску дома. Краска защищает дом от воздействия внешних факторов (в том числе и дождя), но со временем эффект воздействия капель дождя будет накапливаться, что приведет к эрозии. В противном случае специальный защитный слой из материала, способного эту эрозию выдержать, прослужит намного дольше. В будущем ученые намерены уделить этому аспекту больше внимания, проведя опыты, нацеленные на определение материалов и текстур, противостоящих эрозии ударных капель.
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?


